基于决策融合与机器学习的铁路道岔故障诊断

张玉霞

(陕西交通职业技术学院,轨道交通学院,陕西,西安 710018)

0 引言

在铁路运输中,铁路道岔故障严重影响了铁路运行效率和安全,若不及时对道岔进行识别和诊断,极易出现重大交通事故。因此,对道岔健康进行实时诊断和提前预防具有重要意义。然而,传统的铁路道岔故障诊断依旧采用人工诊断方式,存在诊断时间长、效率低和准确率低的问题。针对此问题进行的研究有:杨菊花等[1]提出了基于CNN-GRU模型的道岔故障诊断算法研究,利用CNN网络的深层特征学习特性,与GRU网络相结合,很大程度上提升了道岔故障的准确率;谢博才等[2]深入探索了基于机器学习的道岔故障诊断与预测,利用机器学习中的BP神经网络对道岔故障进行特征提取,实现了道岔故障诊断的有效性;李婉婉等[3]提出基于GMM聚类和PNN的道岔故障诊断研究,将GMM聚类与PNN进行决策融合,发挥两者的优势,使得故障诊断误差减小,诊断效率和准确率提升。结合以上学者研究成果,本文提出将机器学习和决策融合技术相结合,构建基于PNN决策融合道岔故障诊断模型,通过该模型实现道岔故障准确诊断,降低安全事故发生概率。

1 PNN道岔故障诊断模型构建

概率神经网络(PNN)是根据统计原理进行分析的前馈网络,具备分类准确率高的优点[4],其网络结构主要分为输入层、模式层、求和层和输出层等4个部分,具体结构如图1所示。

图1 PNN网络结构

输入层主要负责对样本数据进行接收,数据维度与神经元相对应,输入层单个神经元的输出表示为

(1)

式(1)中,Wi表示输入层与模式层间的连接权值,δ表示平滑因子[5]。通过式(1)可求出求和层样本集类别的概率密度函数(PDF),其类别与求和神经元一一对应。

输出层负责将上层的最大的概率密度进行输出,其输出神经元个数与上层对应[6]。

PNN故障诊断中,若故障类别表示为θA、θB,需判断的故障样本X=(x1,x2,…,xn)表示为

hAlAfA(X)>hBlBfB(X)

(2)

X∈θA

(3)

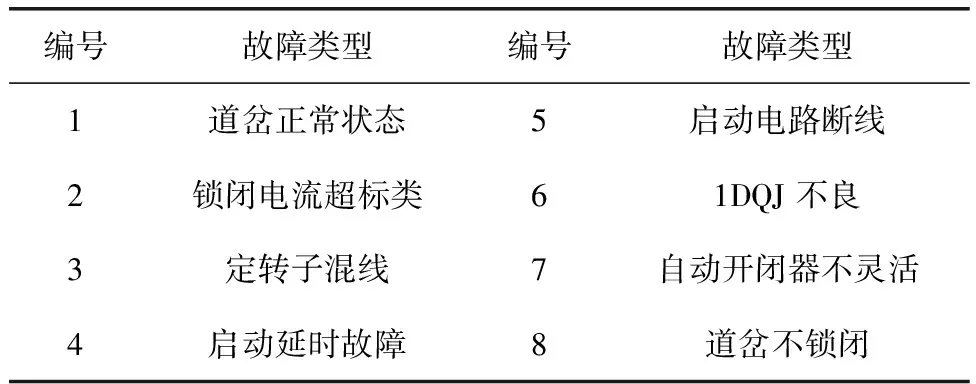
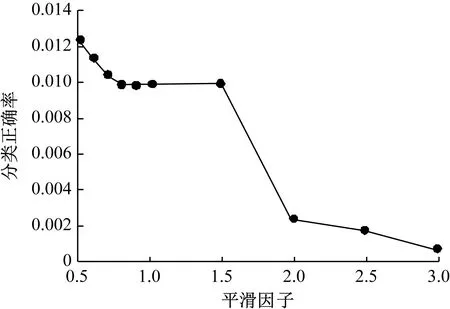
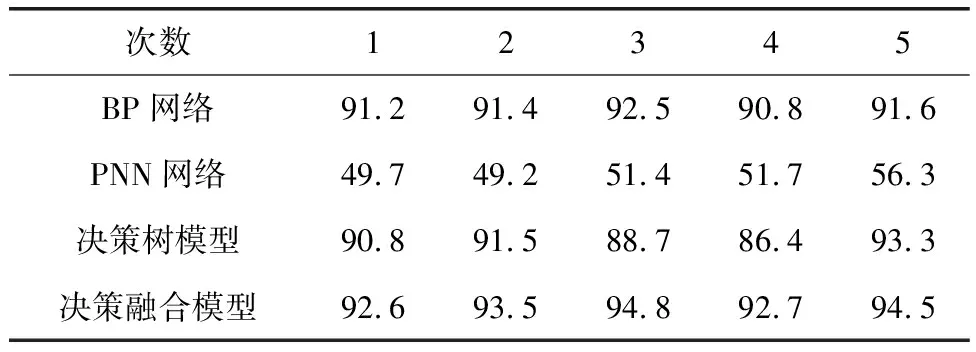
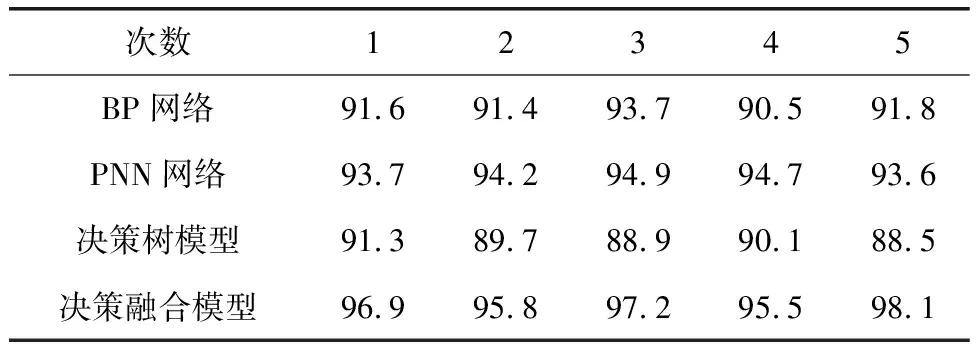
hAlAfA(X)

(4)

X∈θB

(5)

式(2)～式(5)中,hA、hB表示故障类别θA、θB的先验概率(hA=NA/N,hB=NB/N),NA、NB分别表示故障类别θA、θB的样本数目[7-10],N表示样本总数,lA表示属于θA类但划分至θB类的代价因子,lB反之,fA、fB表示故障类别θA、θB的概率密度函数。

道岔故障诊断属于非线性问题,通过PNN网络能对非线性数据进行处理,因此构建基于PNN网络的道岔故障诊断模型,见图2。

图2 PNN故障诊断模型

图2中,采集训练集数据后,即可建立平滑因子可变的PNN网络,找出最佳平滑因子,确定参数,提升PNN网络故障诊断正确率[11];最后建立PNN网络,并利用测试集进行网络测试,由此得到诊断结果。

2 基于 PNN 决策级融合的故障诊断

2.1 PNN 决策级融合故障诊断原理

为进一步提升故障诊断模型的预测能力,在结合PNN故障诊断基础上,融合BP和决策树的诊断模型,从而发挥决策融合技术和PNN网络的优势,降低错误判断率。具体思路如图3所示。

图3 基于PNN决策级融合故障诊断模型原理

首先采集道岔样本集;然后将样本分别输入至各模型中进行训练和测试,输出各模型的预测数据并进行归一化处理;再利用平滑因子选出最优预测参数;最后将最优平滑因子输入基于PNN网络的故障诊断模型中,最终完成道岔故障诊断。

2.2 决策级融合的故障诊断模型构建

基于图3的模型构建原理,构建基于PNN决策级融合的故障诊断模型如下。

(1) 对采集的原始数据进行预处理,获得样本集。

(2) 利用MATLAB构建基于BP网络、决策树和PNN网络的故障诊断模型,进行比较分析后,将训练测试完成的模型用于PNN决策级模型[12]。

(3) 将输入层和输出层分别设置为3个和8个神经元,且输入和输出分别为道岔状态类别编号。PNN决策级融合结构如图4所示。

图4 PNN决策级融合结构

(4) 最后分别对基于PNN的决策级模型和初始模型在初始模型失效和模型完好的情况下进行模型性能测试,判别此模型故障诊断正确率是否得到提升。

3 实验结果与分析

3.1 实验环境

为了验证构建模型的有效性,实验开发铁路道岔系统,软件平台选用Pycharm 2017,Visual Studio 2017,硬件平台的处理器型号为Intel(R)Core i5,选择Windows 7作为操作系统,开发语言为Python,C#。

3.2 实验数据

为了取得更好的实验效果,本次实验数据来自某铁路段监测系统对ZD6 型道岔设备采集的故障动作电流数据。正常的ZD6 型道岔动作电流如图5所示。

图5 正常的道岔电流

通过图5可以看出,道岔动作电流曲线包含10个关键点,标记为T1～T10。根据道岔控制电路原理,图5的电流曲线可分为3步,总共4个时间段。T1～T2表示1DQJ 吸起到道岔动作点,此时动作时间一般在0.2～0.3 s,动作电流一般在6～10 A;T2～T9 为道岔动作至锁闭,该阶段电机电流大、转速慢,同时道岔电流通过转换后,此时的曲线比较平滑;T9～T10为电流记录结束区,此时电流值降为0。通过对动作电流曲线的分析,将道岔状态分为8类,包含7种道岔故障和1种正常状态,具体见表1。

表1 本实验道岔故障类型

选择t=(0.1,0.3,0.5,0.7,0.9,2.0,3.0,4.0,5.0,5.5,6.0,6.5)共12个瞬时电流值为特征信息,采集到的数据共1200条,然后按照8∶2的比例分为训练集960条和测试集240条。由于故障样本相对较少,所以选择其中的720条正常样本和480条故障样本。在完成上述样本数据集构建后,输入MATLAB软件中进行分析仿真。

3.3 参数设置

3.3.1 BP神经网络参数

为达到最好的故障诊断效果,同时方便进行对比,设定隐含层神经元数目为14,网络训练的精度设定为0.001,最大训练步长设定为2000,网络学习的速率设定为0.1,同时采用均方误差作为评价函数。在以上基础数据下,比较不同训练函数和最佳隐藏层节点对训练结果的影响,具体结果见表2和图6。通过表2看出,选择trainlm训练函数得到的均方误差最小,且当隐含层数为11时网络训练误差最小。

表2 不同训练函数下的预测均方误差

图6 不同隐含层数下的网络训练误差

综上,BP神经网络的训练函数选择trainlm,隐藏层节点数设定为11。

3.3.2 PNN参数设置

结合PNN网络结构,将输入层维度设定为12,输出层维度为8,同时采用试凑法对PNN平滑因子进行优化,具体结果如图7所示。

图7 不同平滑因子对分类正确率的影响

通过图7得出,当 SPREAD 为 0.5 时,模型正确率超过 95%,因此选其作为最优平滑因子进行最终网络测试。

3.3.3 决策树参数

决策树的参数设定为max_depth=15,max_features=0.999,min_sampe_leaf=1.0,min_sample_split=25。

3.4 评价指标

选用准确率(P)、漏报率(MA)和虚警率(FA)作为故障诊断结果评价指标,具体计算式为

(6)

(7)

(8)

式(6)～式(8)中,TP、TN、FP、FN分别表示真正例、真反例、假正例和假反例。

3.5 基于PNN决策级融合故障诊断模型验证

完成以上单一诊断模型测试后,对基于PNN决策级融合的故障诊断模型进行验证和分析。分别在某一模型失效和模型完整两种情况下进行验证,通过2种方式测试决策级模型是否具备容错性以及模型正确率是否得到提升。

3.5.1 某一模型失效情况下验证与分析

(1) BP网络失效或PNN网络失效

将测试集的数据应用到基于PNN决策级融合的故障诊断模型中进行测试,当模型正确率低于60%时,说明此模型失效。对模型参数进行优化后,得到最终输出的正确率模拟模型失效情况,如图8、表3、表4所示。

表3 BP网络失效正确率统计表 单位:%

表4 PNN网络失效正确率统计表 单位:%

由图8、表3、表4可知,在BP模型或PNN模型失效情况下,决策级融合模型的预测正确率均保持在92%以上,预测效果较好,没有发生明显变化,说明决策级融合模型具有较高的容错性。

(2) 决策树失效或BP和决策树网络失效

利用测试集进行测试,结果如图9、表5和表6所示。

表5 决策树失效情况下正确率统计表 单位:%

表6 BP和决策树网络失效情况下正确率统计表 单位:%

图9 决策树失效或BP和决策树网络失效情况下的关系图

从图9、表5、表6可知:在决策树失效情况下,决策级融合的预测准确率高达98.7%,均保持在94%以上;而在BP和决策树网络失效情况下,决策级融合的预测准确率依旧在91%以上。由此说明,决策树失效或BP和决策树网络失效对决策级融合的影响较小,该模型具备容错性。

3.4.2 初始模型完好情况下的验证与分析

在3种初始模型完好的情况下,通过5次不同测试集对决策级模型进行测试,测试结果如图10、表7所示。

表7 初始模型完好情况下正确率统计表 单位:%

图10 初始模型完好情况下正确率

由图10、表7可知,在3种初始模型完好状况下,决策级融合模型的预测效果依旧高于3种初始模型,且该模型的诊断正确率均在95%以上,高达98.1%,说明此模型的正确率得到提升。

完成准确率是否提升的测试后,利用测试集对PNN决策级模型进行测试,得到实际类别与预测类别的结果,如图11、图12所示。

图11 PNN决策级融合模型实际图与预测图

图12 PNN决策级融合模型各类别正确率统计图

从图11、图12可以看出,PNN决策级融合模型的正确率为98%,明显高于另外3种模型,漏报率和虚警率仅为3%,由此说明决策级融合模型的正确率得到提升,误判率和漏判率下降,对道岔故障诊断具有较好的识别和分类效果。

4 总结

综上,构建的基于PNN决策级融合故障诊断模型具备可行性和有效性,故障诊断的正确性进一步提升,并具有一定的容错性,模型性能优越。实验结果表明,在单一模型失效情况下,决策级融合模型依旧可以保持较高的准确率。同时,对比完好状况下的模型,决策级融合模型的诊断正确率高达98.1%,比BP网络、PNN模型和决策树提升了6.3%、4.5%和9.6%,模型预测能力显著提升。