生态河道直角折线堰淹没特性分析

周鑫宇，邱 勇，杨昌文，郭金楠，刘毅恒

(云南农业大学 水利学院，云南 昆明 650201)

对于高原山区而言，受季节性降雨影响，城市周边中小型河道流量变化较大[1]，为预防洪涝灾害的发生，往往需要保持河道畅通，避免洪水滞留；但雨季结束后，河道中雨水存蓄量显著降低，导致河道干涸，对河道原有生境造成破坏[2]。为此，需要在中小型河道治理中增设挡水建筑物，以达到存蓄雨水，保证河道所需生态流量。作为亲水设施的直角折线堰不仅溢流效果优美，有利于营造和谐美丽的生态氛围，也能够在兼顾河道生态环境的同时保证防洪安全。

相较于传统挡水建筑物，直角折线堰整体构造简洁[3]，在平面布置上呈折线形，能够在中低水头时有效增加溢流前缘长度，从而提高过流能力[4]。目前，针对自由出流情况下的直角折线堰，周鑫宇[5]等基于试验研究，给出了直角折线堰的溢流特性；邱勇[6]、李庆梅[7]、王尚今[8]等分别给出了直角折线堰不同布置的流量系数计算公式。但当下游河道有树木或其他物体沉积时[9-10]，很可能迫使河道下游水位升高，改变直角折线堰溢流条件；或者在遭遇超标洪水时，过堰水深加大，堰体完全淹没，无法发挥控制水流作用。因此，研究直角折线堰的淹没出流，能够对中小型生态河道治理提供很好借鉴。

1 数学模型

1.1 模型构建

在河道宽度为w的中小型河道中，直角折线堰几何参数包括：前堰长度a、侧堰长度b、后堰长度c、堰高P及堰体厚度d，其中，河道宽度w=a+c，溢流前缘长度L=a+b+c，其平面布置如图1所示。模型体形分为：①固定侧堰长度不变(b=112.5mm)；②改变侧堰位置(a=37.5、75、112.5mm)；③固定侧堰位置不变(a=c=75mm)，增加侧堰长度(b=75、112.5、150mm)，其中河道宽度w=150mm，堰高P=100mm，堰体厚度d=10mm。

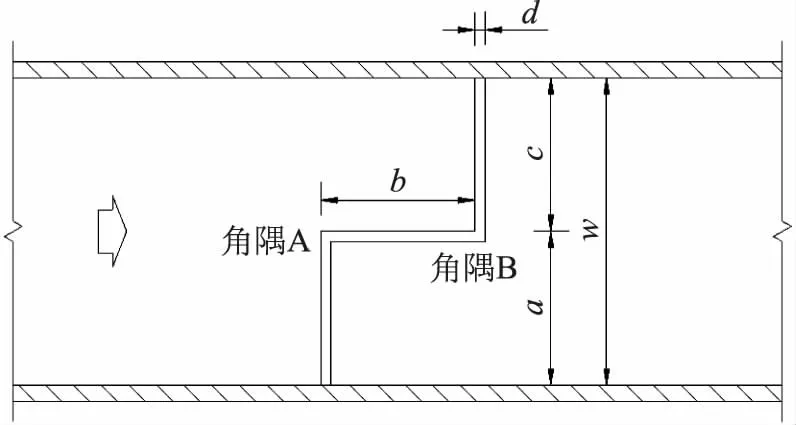
图1 直角折线堰平面布置

1.2 网格划分及边界条件

采用FLOW-3D数值仿真软件建立计算模型(如图2所示)，模型计算域以侧堰和后堰交点为坐标原点，x方向为河道宽度(xmin=-75mm，xmax=75mm)，y方向为河道长度(ymin=-370mm，ymax=450mm)，z方向为河道深度(zmin=0，zmax=400mm)，采用结构化网格，将计算域划分为一个网格块，每个网格单元均为1.8mm×1.8mm×1.8mm的正方体，网格总数约为850万(如图3所示)。

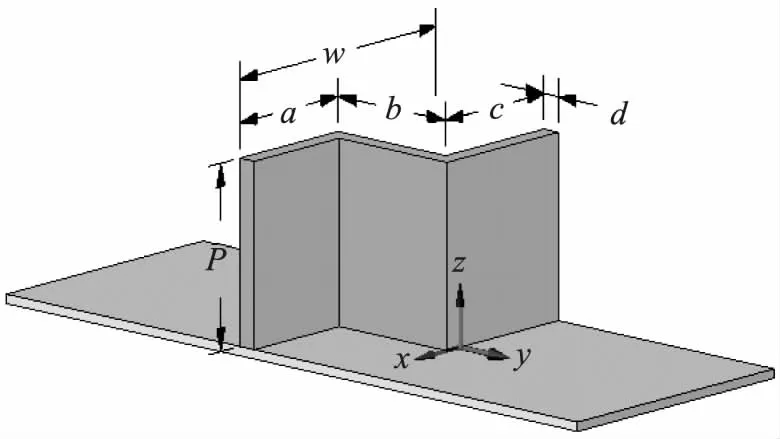
图2 直角折线堰概化模型

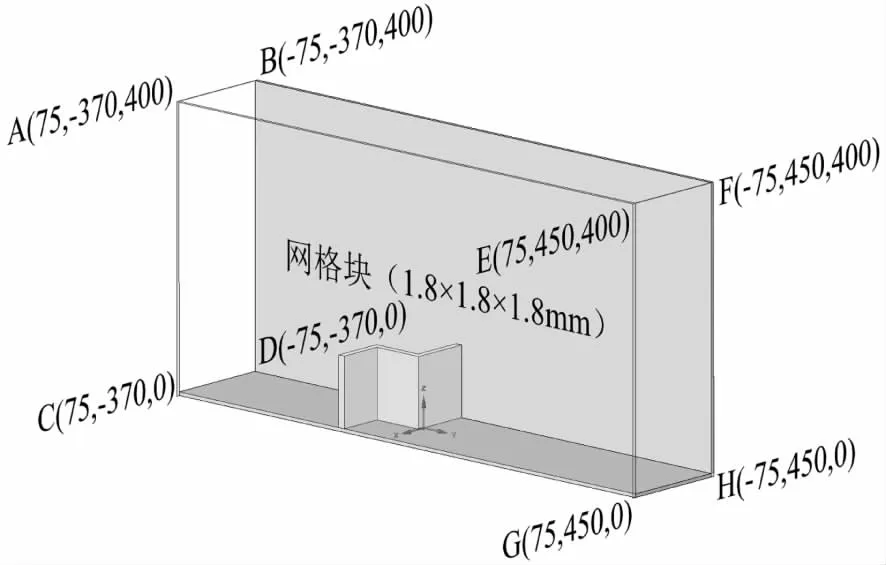
图3 网格划分

为反映直角折线堰溢流特性随流量变化情况，将水流进口设置为流量边界；出口采用压力边界，设置流体高度为相应下游水位；顶部同样采用压力边界，流体分数设为0(初始条件下只存在空气)；河道底部及边墙均采用无滑移固壁边壁条件，并分别在进口、出口、前堰、侧堰和后堰位置设置流量监测面，以获取堰体各部分的流量大小(如图4所示)。数学模型采用RNGk-ε模型[11-12]，气液自由表面追踪采用Tru VOF方法[13-14]。

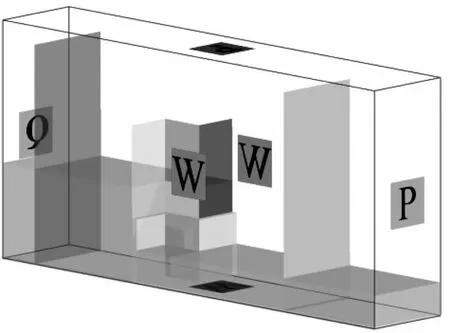
图4 边界条件

1.3 数学模型率定

采用7组流量Q=4、6、8、10、12、14、16L/s计算各体形的过流能力，应用已有成果文献[8]中给出的直角折线堰试验数据进行模型验证(见表1)。

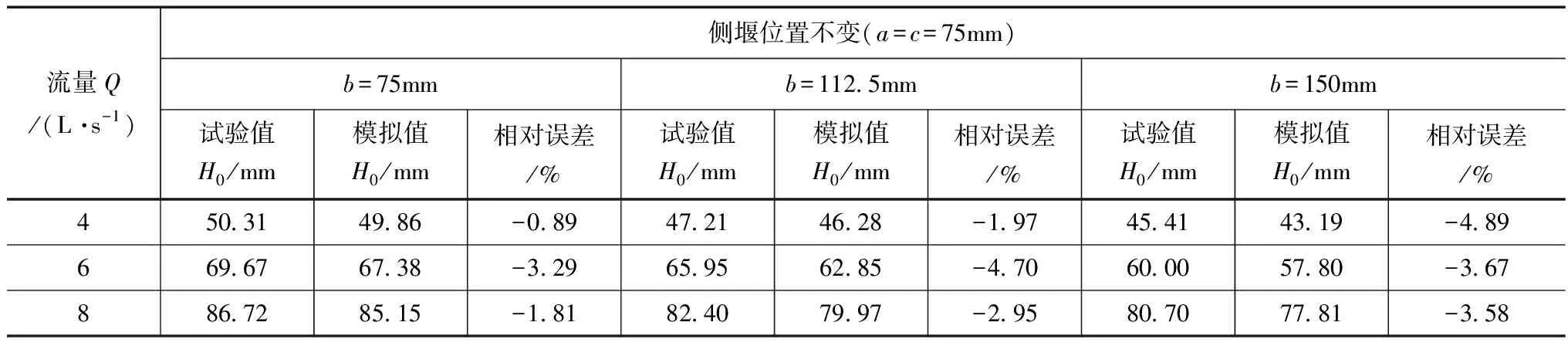
表1 数值模拟与试验研究过流能力对比表

由表1可以看出，在流量分别为Q=4、6、8L/s时，不同体形的流量模拟值与试验成果极为接近，最大误差为4.89%，表明所建立的数学模型可以模拟直角折线堰溢流过程。

2 成果与分析

2.1 过堰水流流态

直角折线堰出现淹没水流的流态与薄壁堰[15]淹没流态类似，由潜射底流依次过渡到破碎波、表面波和表面出流(如图5所示)，直至完全的淹没出流。

下游水位低于堰顶高程时，前堰、侧堰和后堰过堰水流均呈潜射底流状跌落下游河床(自由出流)。当下游水位超过堰顶后(如图5(a)所示)，前堰、侧堰过堰水流仍保持潜射底流状；前堰、侧堰过堰水舌下方，部分水体向堰体侧翻卷，并汇聚在后堰过堰水舌下方形成水流轴线方向的顺时针螺旋状水流，后堰过堰水舌受其顶托，开始集中于表层，在其水舌上方形成小幅旋滚的回淹水流。

随着下游水位的逐渐壅高(如图5(b)所示)，前堰过堰水舌依旧下潜冲向河床，侧堰过堰水舌出现顶托，后堰过堰水舌则完全集中于表层，致使下游水体表面呈破碎波状。流量进一步增大(如图5(c)所示)，前堰过堰水舌出现顶托，侧堰和后堰主流集中于表层流动，下游4倍侧堰长度范围内可观察到水面的小幅波动。当下游水位高于2.70倍堰高时，直角折线堰处于完全淹没状态，前堰、侧堰、后堰过堰主流均处于表层，但水流相对平顺，形成较为明显的表面出流(如图5(d)所示)。

2.2 直角折线堰淹没出流

对于直角折线堰而言，自由出流过渡到完全淹没时的水流流态如图6所示。

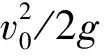
采用无量纲水头法[16]计算绘制hs/H0～Hu/H0关系曲线，得到直角折线堰包括临界淹没度(Hu/H0=1)和完全处于淹没时(hs=Hu)的变化过程。如图7所示，为直角折线堰在侧堰位置改变(长度不变)时的hs/H0～Hu/H0关系曲线。

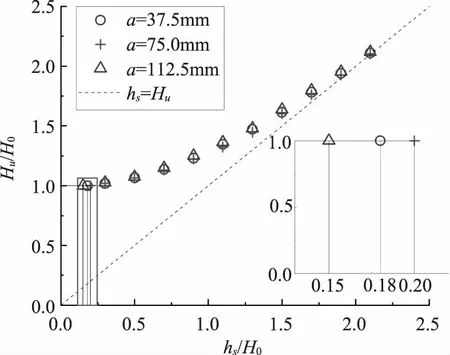
图7 侧堰位置变化下的hs/H0～Hu/H0关系曲线(b=112.5mm)

由图7可以看出，当侧堰位置靠近河道右岸(a=37.5mm)时，直角折线堰在hs/H0≥0.18(Hu/H0=1)后开始出现淹没；但随着侧堰位置变化至河道中部(a=75.0mm)和靠近河道左岸(a=112.5mm)时，反映直角折线堰出现临界淹没现象的hs/H0呈现先增加(0.20)后减小(0.15)的变化趋势。表明侧堰位于河道中部时，直角折线堰能够保持更长的自由出流时间。特别是当hs/H0>1.90后，堰体上下游水位已经齐平(hs=Hu)，此时直角折线堰已无从发挥流量控制作用。侧堰长度改变(位置不变)时的hs/H0～Hu/H0关系曲线如图8所示。

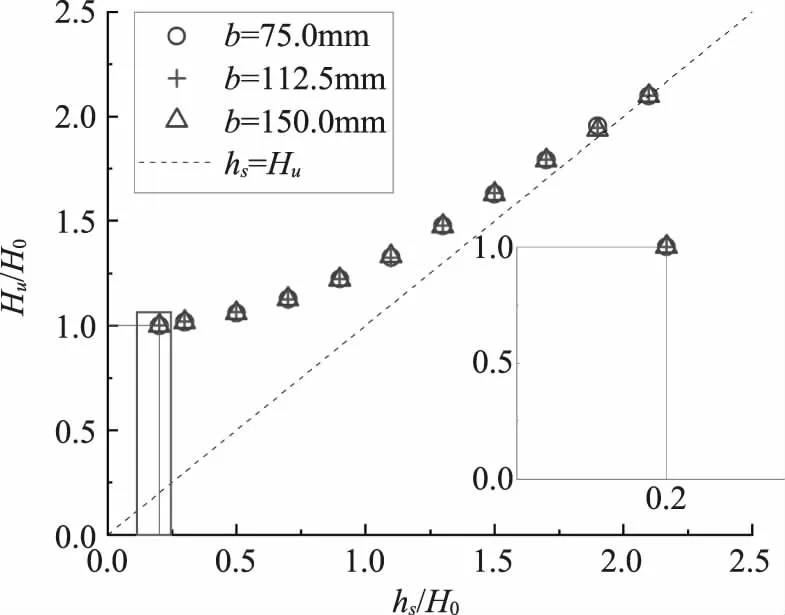
图8 侧堰长度变化下的hs/H0～Hu/H0关系曲线(a=c=75mm)

由图8可以看出，侧堰长度的增加，对直角折线堰自由出流向淹没转化影响不明显，均能够在hs/H0≤0.20附近时，保持自由出流。同样的，随着堰顶以上的下游水深与自由出流时的堰顶全水头之比hs/H0>1.90后，直角折线堰呈完全淹没状态(hs=Hu)。

2.3 直角折线堰淹没度

2.3.1淹没条件下的过流能力

在堰流基本公式中，通常采用河道过流宽度w来计算得到溢流堰的过流能力。但在直角折线堰中，其在实际溢流过程中过流宽度是变化的，因此，依据河道宽度w计算得到的直角折线堰流量系数为有效溢流前缘长度和淹没系数共同影响下的过流能力，定义为名义流量系数Mw。在侧堰长度不变，位置改变时的过流能力及名义流量系数Mw见表2。

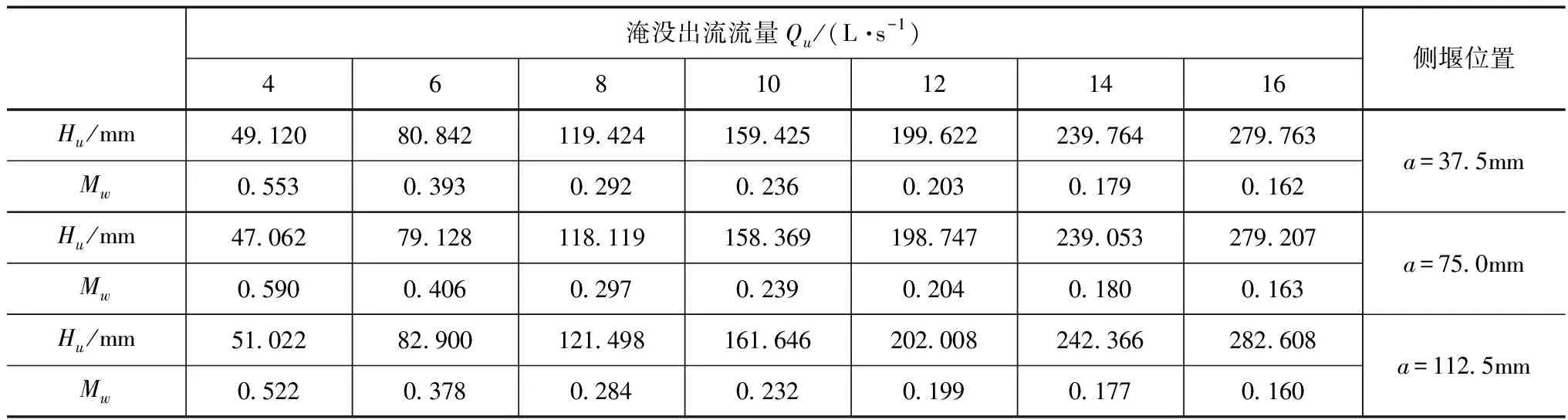
表2 侧堰位置变化下(b=112.5mm)的名义流量系数Mw

由表2可以看出，随着流量的增加，直角折线堰在不同侧堰位置的堰顶水头逐渐增大，但其名义流量系数Mw呈下降趋势：流量由4L/s增加至6、8L/s，前堰长度a=37.5mm(侧堰位置靠近河道右岸)时的Mw由0.553减小至0.393、0.292。

保持侧堰位置不变，改变其长度时的过流能力和名义流量系数Mw如图9所示。

图9 侧堰长度变化下(a=c=75mm)的过流能力及名义流量系数Mw

由图9可以看出，随着堰顶水头的增加，直角折线堰流量增大，但增幅逐渐下降：当侧堰长度b=112.5mm，堰顶水头由100mm增加至120、140mm时，过流能力增幅由14.46%减小至12.28%，此时名义流量系数Mw也由0.348下降至0.294、0.265；增加侧堰长度至b=150.0mm时，其Mw依旧呈下降趋势：流量由6L/s增加至8、10L/s时，Mw由0.420下降至0.302、0.242。

2.3.2有效溢流前缘长度变化

从图5的淹没出流过堰水流流态变化也可以看出：实际的流量系数计算应该考虑溢流前缘长度随堰顶水头增加的变化影响。自由出流向淹没出流转化时，直角折线堰过堰表层水流流线变化情况如图10所示。

图10 直角折线堰过堰水流流线变化情况(a=c=75mm，b=112.5mm)

当直角折线堰处于自由出流时，侧堰过堰水流流线与堰体近呈正交，此时，直角折线堰有效溢流前缘长度为前堰、侧堰和后堰堰体长度之和。随着流量的增加，淹没出现的同时，侧堰过堰水流流线方向与堰体斜交，致使侧堰溢流前缘长度减小；流量进一步增大，堰体对流量的控制作用丧失，侧堰过堰水流流线已经与侧堰方向平行，直角折线堰有效溢流前缘长度近似等于河道宽度。

考虑有效溢流前缘长度变化对直角折线堰过流能力的影响[8]，得到在不同淹没流量下，直角折线堰侧堰长度改变(位置不变)时的有效溢流前缘长度变化及综合流量系数ML(有效溢流前缘长度计算得到的流量系数定义为“综合流量系数ML”)如图11所示。

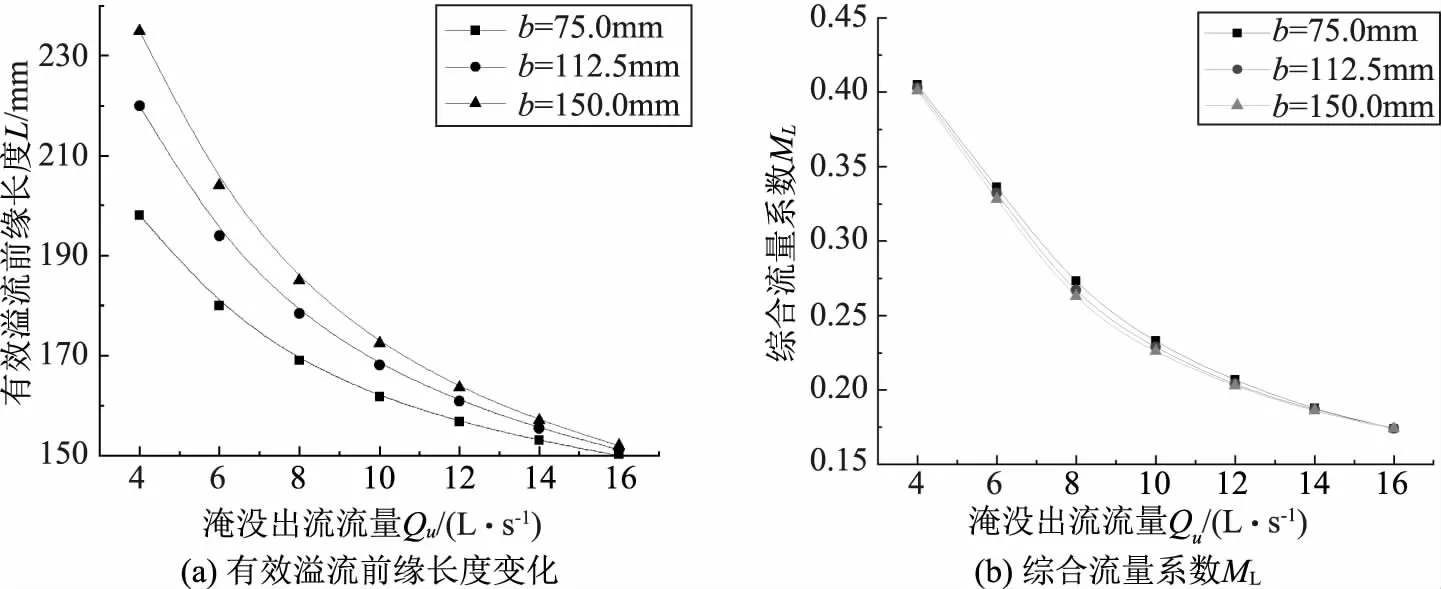
图11 侧堰长度改变(位置不变)时的有效溢流前缘长度变化及综合流量系数ML(a=c=75mm)

由图11(a)可以看出，随着流量的增加，直角折线堰有效溢流前缘长度逐渐下降，并趋近于河道宽度(w=150mm)。在此过程中，计算得到直角折线堰综合流量系数ML也呈下降趋势(如图11(b)所示)：流量由4L/s增加至6、8L/s时，当侧堰长度b=112.5mm的ML由0.404下降至0.332、0.268，和自由出流情况下流量系数变化规律相反。

由此可以推知，直角折线堰淹没出流条件下的综合流量系数ML已经包括了淹没系数σL影响(ML=σLmL)。

2.3.3淹没系数

考虑有效溢流前缘长度变化，按照自由出流的流量系数mL，计算得到直角折线堰不同流量下的淹没系数σL(见表3)：

表3 考虑有效溢流前缘长度变化的淹没系数σL(a=c=75mm，b=112.5mm)

为方便应用，通过堰流基本公式计算直角折线堰在河道固定宽度(w)下，依据其不同布置在自由出流时的流量系数mw和淹没出流时的名义流量系数Mw(见表2、如图9所示)，得到流量变化条件下，直角折线堰淹没系数σw与相对淹没度hs/Hu关系如图12所示。

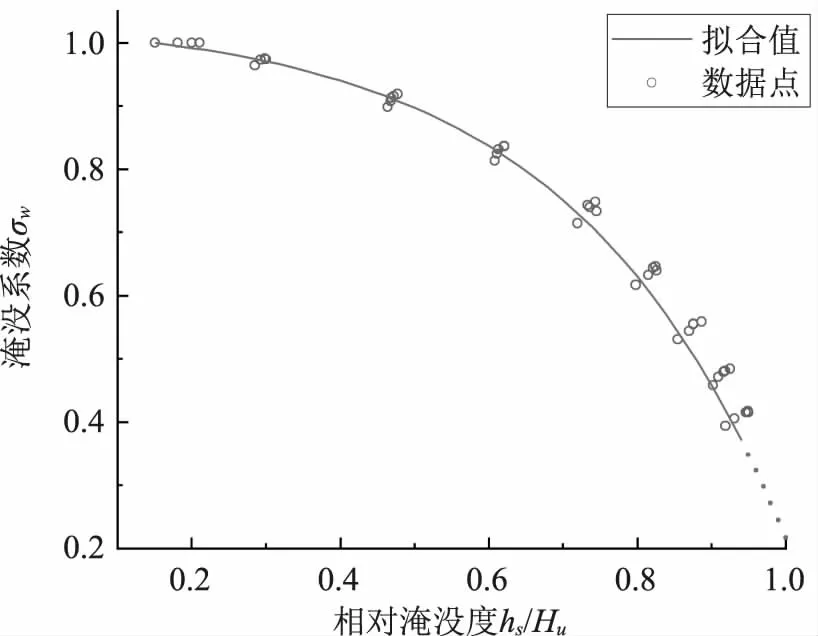
图12 直角折线堰的淹没系数

由图12可以看出，当直角折线堰处于自由出流(淹没系数σw=1)时，其堰顶以上下游水深hs≥(0.15～0.21)Hu。

此外，对于直角折线堰不同布置下的淹没系数σw与相对淹没度hs/Hu关系相差不大，因此，通过公式拟合得到相关性为0.994的淹没系数计算公式(1)来表征不同布置下的淹没系数σw与相对淹没度hs/Hu关系。

(1)

此时淹没出流计算公式可表示为：

(2)

3 结论

通过对不同体形下的直角折线堰淹没特性进行研究，得到以下成果：

(1)对于不同体形的直角折线堰，当堰顶以上的下游水深hs>1.90H0时，直角折线堰达到完全淹没状态，此时的相对淹没度为1，堰体不再具有控制水流的作用。

(2)当侧堰位置改变(长度不变)时，侧堰位于河道中部时临界淹没度最大(较不容易发生淹没)；而单纯改变侧堰长度(位置不变)，其临界淹没度并无明显变化。

(3)随着淹没流量的增加，直角折线堰过流能力呈下降趋势，为便于应用，按照河道过流(固定)宽度的淹没系数σw与相对淹没度关系曲线，拟合得到了可反映淹没特性的直角折线堰淹没出流计算公式。