洋山港拟建码头波浪影响下作业天数统计分析
张婕,梁颖瑜,于芸
(自然资源部东海预报减灾中心,上海 200136)
0 引言
波浪是海洋水文特征要素之一,是岸滩演变、海港和海岸工程重要的动力因素和作用力。在较为开阔的海域环境,港区的系泊船舶因波浪的变化会产生较大幅度摆动,这种摆动不仅对装卸作业造成一定困难,还可能会影响近岸水工结构物稳定性,从而发生较为严重事故。这种事故在我国都曾发生过:例如宝钢马迹山港、大连港万吨矿石专用码头等都发生过多次断缆事故,其原因均为波浪使系泊船剧烈摆动所致。由此可见港区的波浪条件对船舶停泊安全有着重要影响。
洋山深水港是世界上最大的海岛型深水人工港,是上海建设国际航运中心的重要战略基地。洋山深水港自2002 年开工建设以来,已逐渐完成了一期到四期码头建设与围海造地工程,为了增加码头船舶泊位,拟在小洋山北侧开发区外侧建设防波堤,对码头形成较好的掩护条件,形成环抱式港池。而码头的作业天数作为海港码头设计中的重要指标,直接影响到防波堤的平面布置方案、码头吨级、结构选型等诸多方面问题[1]。
曹兵等[2]根据临港新城海域连续1 a 的波浪实测资料,对该海域波浪影响下的不利作业天数进行了统计。柴雪琴[3]利用SWAN 波浪模型及洞头站1 a 的气象资料反推了瓯飞北片港区的泊稳条件,得到各泊位不同吨级船型对应的作业天数,为码头工程建设方案提供科学依据。丁兆宽等[4]采用了MIKE21 软件建立波浪模型数学模型,讨论了不同的平面布置下港区内的泊稳条件。张素等[1]通过建立波浪观测站点与码头前沿水域的波浪关系,进而对波浪影响作业天数进行了统计。可见,利用数学模型结合实际观测资料来统计波浪影响下码头的作业天数是目前最常用的方法。
本文收集了小洋山北侧杨梅嘴观测站15 a 的观测资料,通过建立波浪数学模型,采用张素等[1]提出的作业天数统计方法,对洋山港北侧作业区码头的作业天数进行统计计算,为规划部门优化防波堤的平面布置提供参考。
1 工程概况
1.1 项目简介
为了增加洋山深水港码头船舶泊位,拟在小洋山北侧建设防波堤对码头进行掩护。由于小洋山中部有输油管道通过,因此防波堤的形式为东西两段,在中间进行截断设计,左侧堤长3 000 m,右侧堤长3 500 m,中部管道口宽420 m。具体形式见图1。

图1 防波堤布置方案Fig.1 Layout plan of breakwater
1.2 码头作业标准
影响码头作业的自然条件有很多,波浪、风速、降雨、大雾等等,由于本文主要研究该工程前期设计阶段的码头方案比选,因此只讨论波浪的影响。工程海域主要以风浪为主,涌浪出现频率较小[5],根据JTS 165—2013《海港总体设计规范》[6]和码头建设需求,本文主要讨论波浪小于0.4 m 和波浪小于0.6 m 的情况。
1.3 工程海域波浪资料
收集了小洋山码头西北方向的杨梅嘴观测站1997—2012 年的波浪历史资料,统计得到杨梅嘴观测站波浪频率分布表,由于观测站点观测为H4%波高,在此转化为有效波高Hs(表1)。
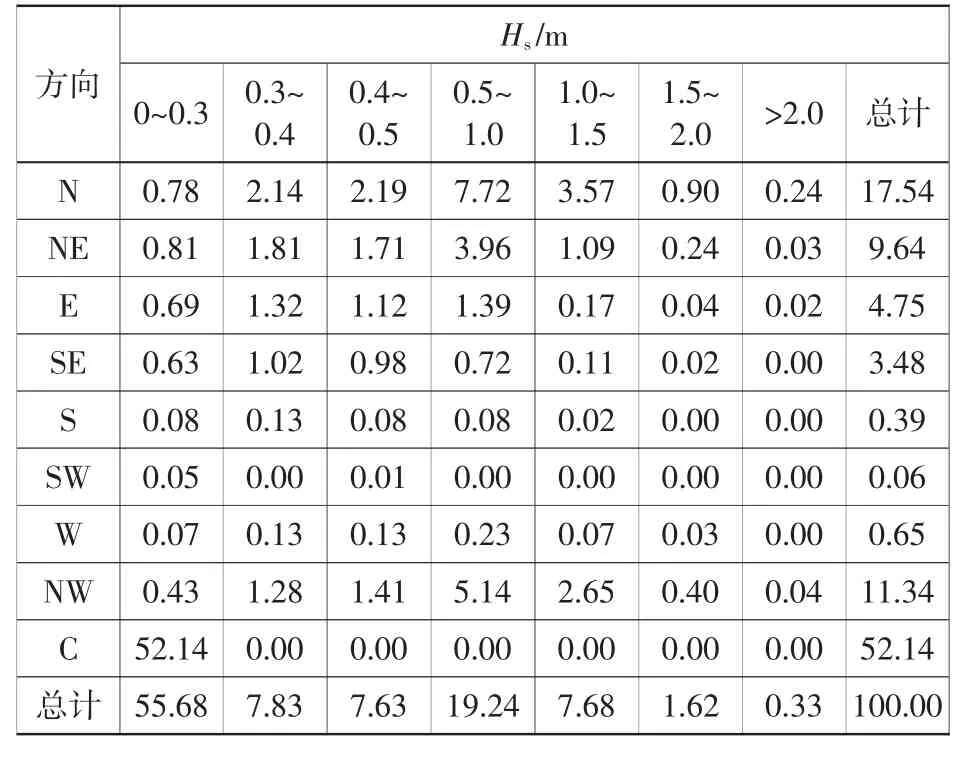
表1 杨梅嘴观测站波浪频率分布表Table1 Wave frequency distribution at Yangmeizui Observation Station %
2 码头作业天数统计
2.1 统计方法
根据张素等[1]文中阐述,本统计方法重要的一点就是计算码头前沿某波向波高与观测站点的关系系数,且推荐采用2 a 一遇的比波高作为关系系数,公式为:
式中:H码头前沿为码头前沿允许作业波高,本文取0.6 m 和0.4 m 分别进行计算;H测点为测波点处允许波高,本文指杨梅嘴站波高。
根据式(1),可由码头前沿允许作业波高求得波浪观测点处的波高,根据波浪观测点处(杨梅嘴)的频率统计资料,统计超过H测点的波高出现频率,最终得到波浪影响作业天数。
根据以上方法,本文需要建立波浪数学模型先来获得码头前沿水域2 a 一遇的比波高,进而求得影响作业天数。
2.2 模型介绍
2.2.1 模型选择
由于防波堤的存在,码头内波浪发生折射、反射和绕射等现象,计算精度要求高,采用目前国内外海浪计算广泛应用的第三代海浪数值计算模型SWAN 进行计算。
SWAN 模型为基于能量平衡方程的谱模式,其基本控制方程为波作用量守恒方程:
式中:N为作用量密度;σ 为相对频率;θ 为波向;方程左边第1 项代表作用量密度随时间的变化率;第2 项和第3 项代表作用量密度在几何空间的传播(以Cx和Cy为传播速度);第4 项代表流和变化的水深引起的频移(以Cσ为传播速度);第5 项代表由流和变化的水深引起的折射和变浅作用(以Cθ为传播速度);S为能量源项。
在球坐标系中,空间坐标以经度λ 和纬度φ表示。
模型主要考虑波浪在近岸的物理过程,包括风能量的输入、底摩擦能量损耗、波浪破碎、波波相互作用、白帽耗散、折射、水流对波浪的作用、波浪绕射等。
2.2.2 模型边界波要素
模型输入边界采用JONSWAP 谱,波要素采用杨梅嘴观测站分方向(8 方位统计)的2 a 一遇H4%波高(P-Ⅲ曲线),波周期采用波高-波周期线性相关统计计算而得(波周期采用1997—2012年观测的大于0.5 m 的波高与波周期线形拟合得出:T=1.693Hs+2.077)[7],见表2。

表2 杨梅嘴2 a 一遇波浪要素Table 2 Wave elements of 2-year return period at Yangmeizui Observation Station
由于杨梅嘴观测站位于工程附近,模型输入未考虑风的作用及相关的物理耗散。
2.2.3 模型设置
模型采用矩形网格,模型空间分辨率为20 m,网格数为1 000×1 000。由杨梅嘴的实测资料分析,在小洋山北侧,工程需要抵御的波浪为NW、N、NE、E 4 个方向。因此,为了有利于模型边界条件输入,本文采用2 套网格进行计算。其中N 向和E 向,采用图1 所示范围,以小洋山为中心,东西和南北向各取20 km;NW 向和NE向采用图2 所示范围,东北和西南向各取20 km。
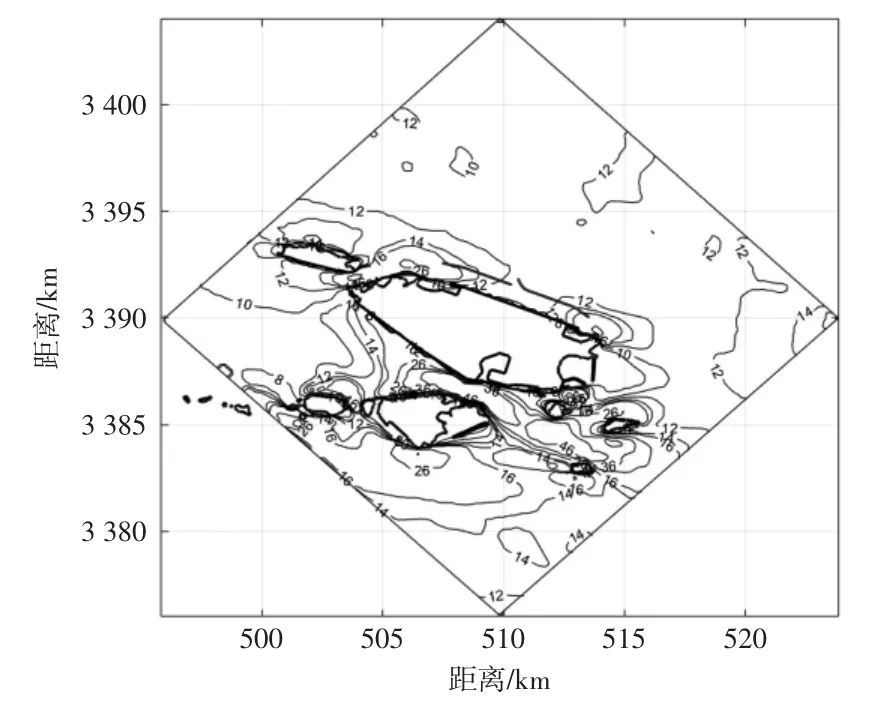
图2 NE 和NW 方向计算区域Fig.2 Calculation area in NE and NW
2.3 计算结果
如图3 所示,取码头前沿A-J10 个采样点波要素计算结果进行统计分析。
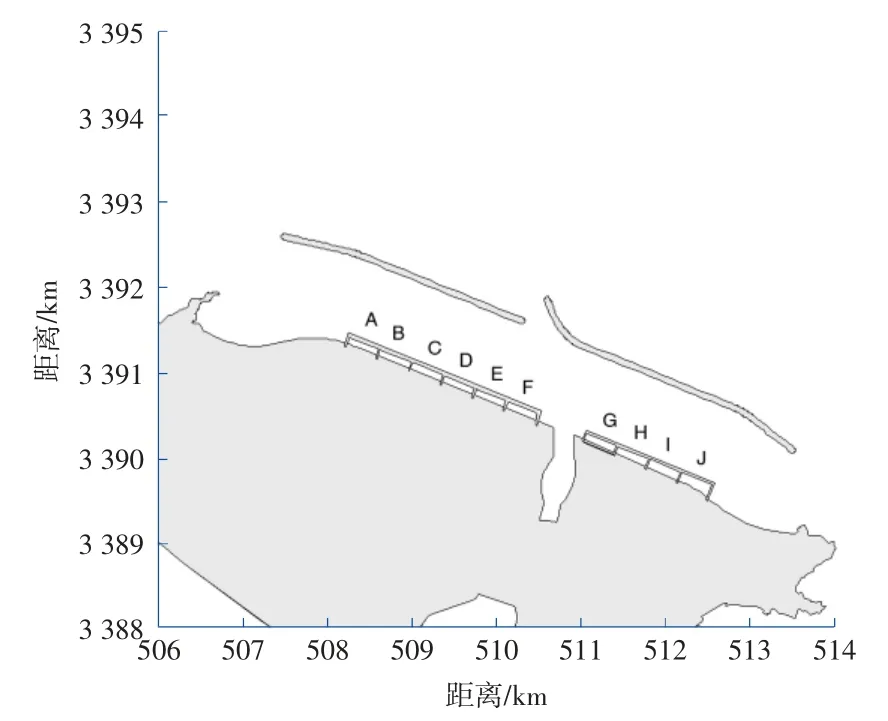
图3 泊位区波浪结果提取区段位置示意图Fig.3 Location diagram of wave data extractions sections in berth area
根据式(1),用数值计算结果得到的每个码头的比波高(见图4),也就是关系系数,结合泊位要求波高H码头前沿(≤0.4 m,≤0.6 m),计算出H测点;根据表1 统计出各泊位各方向大于H测点的频率之和,乘以365 d,最终计算得出各泊位的年不可作业天数。
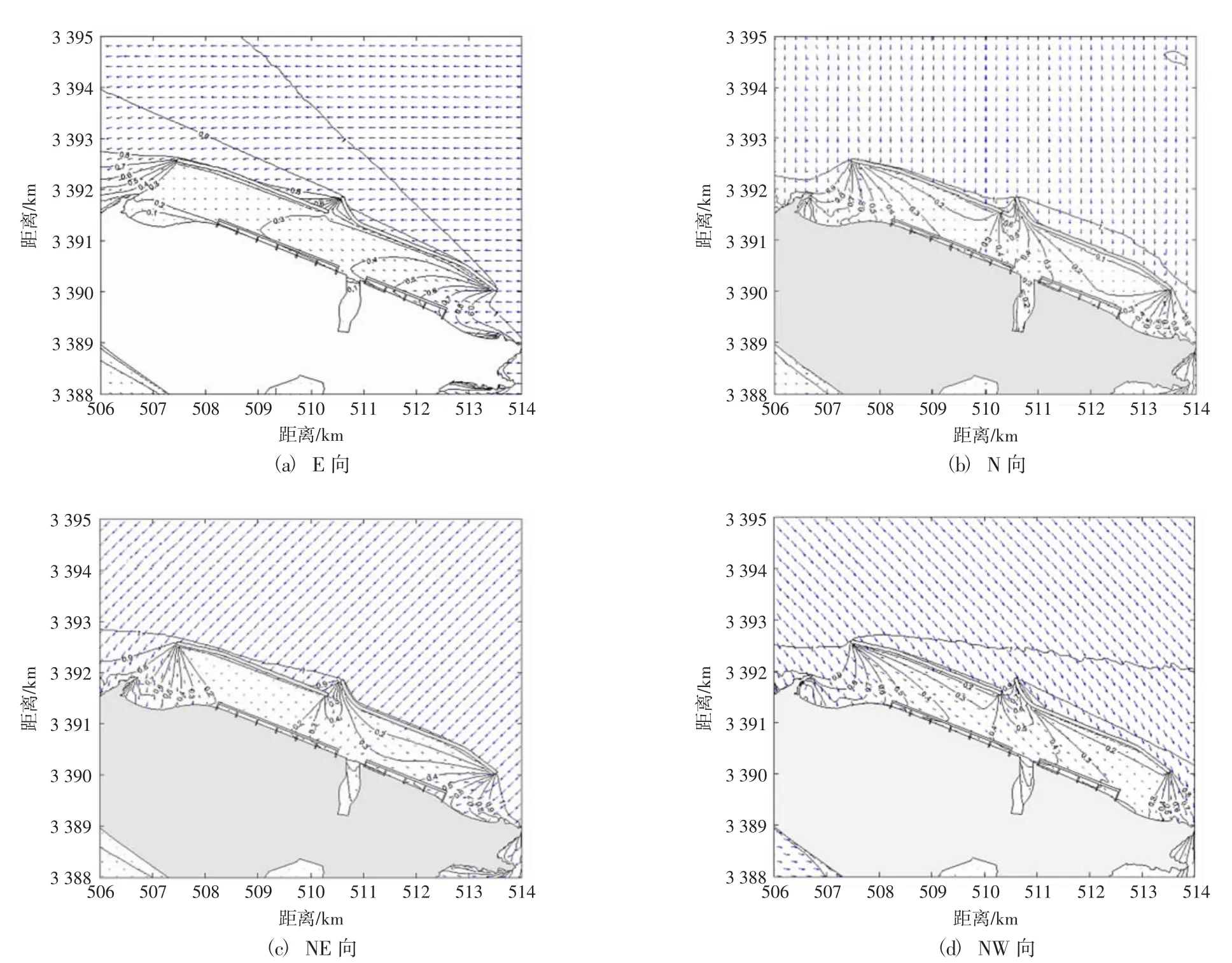
图4 原始方案相对波高分布Fig.4 Relative wave height distribution in original scheme
由表3 可见,在原始方案下,只有A 点处码头在0.4 m 波浪条件下不可作业天数大于30 d(33.9 d),其余各个码头的不可作业天数均小于30 d。

表3 各区段不可作业天数统计(原始设计方案)Table 3 Statistics of non-operational days(original design scheme)
3 补充方案应用
根据本工程平面布置方案,各区段满足30 d以下不可作业仍有富足,为了减少工程造价,节约工程成本,同时验证本文方法的可行性,本文在原始方案基础上进一步讨论了防波堤缩短方案,包含防波堤左侧分别缩短300 m、600 m 和右侧缩短300 m 的方案,计算不可作业天数,见表4—表9。可见,如要求码头作业波浪小于0.4 m,则缩短防波堤方案对不可作业天数影响较大,防波堤左侧缩短300 m 时,已经有4 个区段大于30 d不可作业,当左侧防波堤继续缩短后,增加到6个区段大于30 d 不可作业。值得注意的是中间F区段,由于其处于中心但无防波堤防护处,所以防波堤缩短方案对其影响较大。对于小于0.6 m的波浪,缩短防波堤方案几乎全部可以满足小于30 d 的不可作业时间。
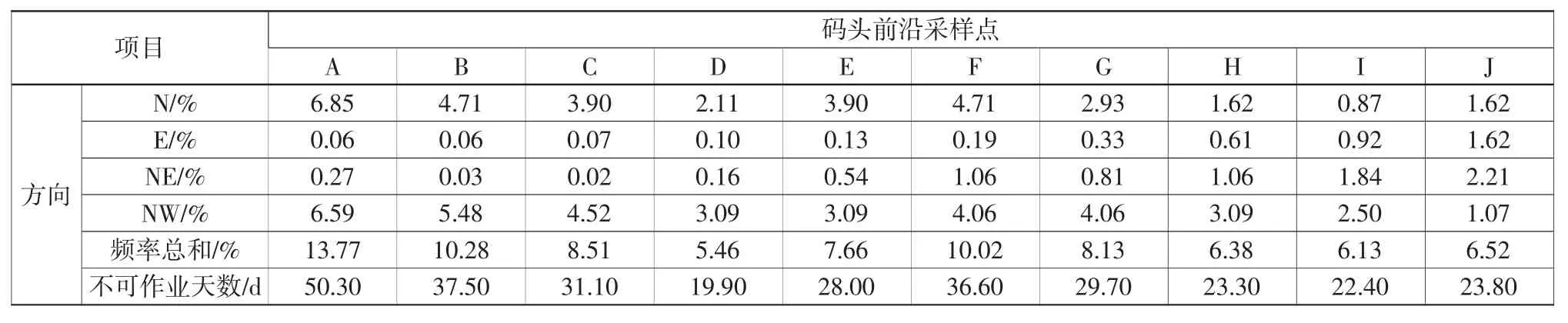
表4 各区段波浪小于0.4 m 不可作业天数统计(防波堤左侧缩短300 m)Table 4 Statistics of non-operational days in various sections when wave height is less then 0.4 m(with breakwater cut short by 300 m on the left side)

表5 各区段波浪小于0.4 m 不可作业天数统计(防波堤左侧缩短600 m)Table 5 Statistics of non-operational days in various sections when wave height is less then 0.4 m(with breakwater cut short by 600 m on the left side)

表6 各区段波浪小于0.4 m 不可作业天数统计(防波堤右侧缩短300 m)Table 6 Statistics of non-operational days in various sections when wave height is less then 0.4 m(with breakwater cut short by 300 m on the right side)
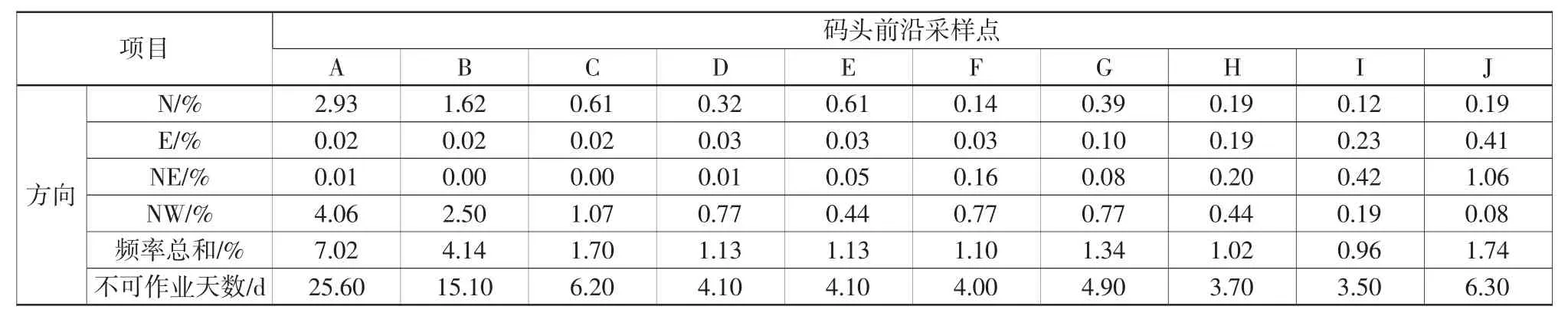
表7 各区段波浪小于0.6 m 不可作业天数统计(防波堤左侧缩短300 m)Table 7 Statistics of non-operational days in various sections when wave height is less then 0.6 m(with breakwater cut short by 300 m on the left side)
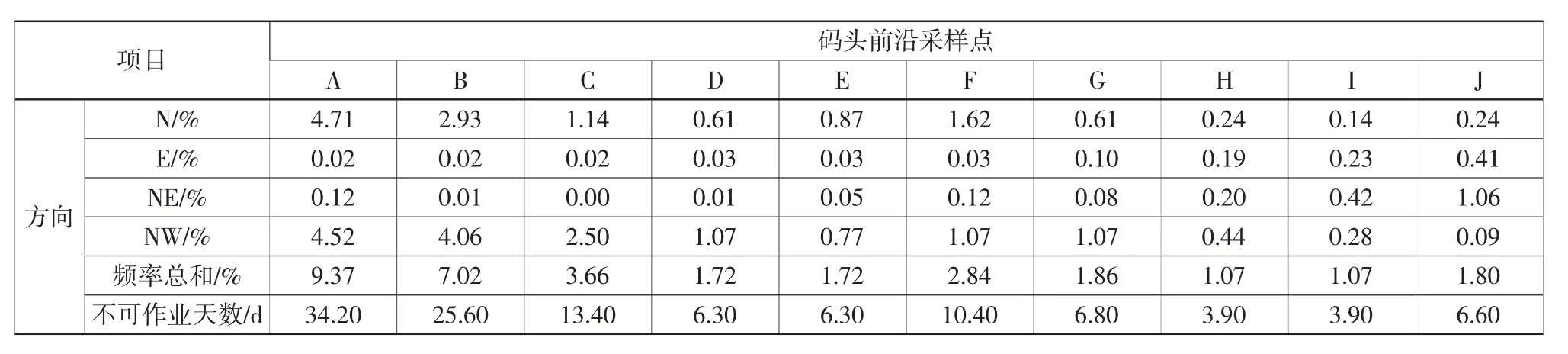
表8 各区段波浪小于0.6 m 不可作业天数统计(防波堤左侧缩短600 m)Table 8 Statistics of non-operational days in various sections when wave height is less then 0.6 m(with breakwater cut short by 600 m on the left side)
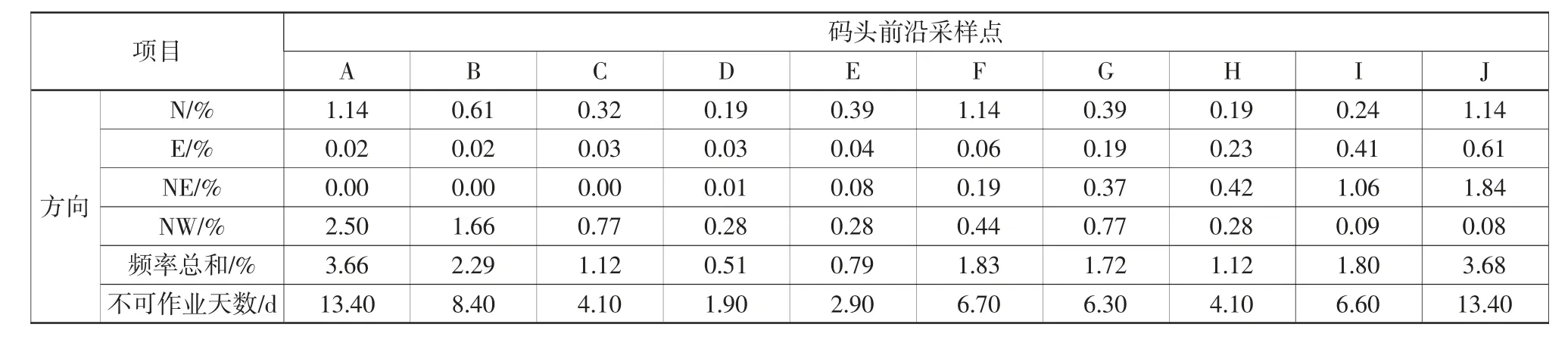
表9 各区段波浪小于0.6 m 不可作业天数统计(防波堤右侧缩短300 m)Table 9 Statistics of non-operational days in various sections when wave height is less then 0.6 m(with breakwater cut short by 300 m on the right side)
4 结语
1) 本文采用SWAN 波浪计算模型,搭建了针对洋山港拟建防波堤的波浪数学模型,并根据杨梅嘴观测资料统计分析,确定了影响工程区域的主要波浪方向为NW、NE、E 和N 共4 个方向。
2) 基于搭建的数学模型和主要波浪方向,采用2 套计算网格,计算2 a 一遇的波浪入射条件下洋山港码头前沿的波浪分布情况。根据模型计算波高和入射波高的比值,求得码头处的相对波高。以码头处允许作业波高(0.4 m 和0.6 m)为基准,反向推导出实测站点的允许作业波高,结合实测站点的频率统计,最终求得码头处不可作业天数。
3) 本文针对洋山港拟建码头处不可作业天数的统计研究,证明采用波浪数学模型建立波浪观测站点和码头前沿波浪的关系,进而统计波浪影响作业天数的方法有效可靠,可为同类项目前期设计提供参考。

