多振荡浮子式波浪能平台水动力数值模拟研究
刘枫,金瑞佳,刘飞,畅涛,王军
(1.交通运输部长江航道工程局有限责任公司,湖北 武汉 430000;2.交通运输部天津水运工程科学研究所,天津 300456;3.青岛正海航务工程有限公司,山东 青岛 266500;4.宁波市港航管理中心,浙江 宁波 315042)
0 引言
为了应对能源危机所带来的巨大挑战,探索清洁可再生的新能源已成为世界各国的当务之急。作为一种新型清洁能源,相比于其他可再生能源,波浪能具有十分明显的优势。波浪能的能量利用效率比较高,其在可再生能源中具有最高的能量密度,且开发和利用波浪能的过程对于环境以及水生生物的影响非常小。此外,波浪能发电装置可在90%的时间内运行,而风能利用设备和太阳能利用设备的运行受环境影响非常大,正常工作的时间仅为波浪能的三分之一。Zhang 等[1]曾经综述过中国的波浪能技术,并提出了发展方向和前景,希望有更多的国际间合作来分享相关经验。
波浪能利用技术历经了百年的发展史,目前已经有了许多的实际应用。针对振荡浮子式波浪能装置,很多国家已经有样机陆续投入使用。挪威开发了浮标式振荡浮子装置[2]。瑞典研发的L9震荡浮子装置[3],以扁圆柱体为浮子作为能量吸收体,装置所采用的发电机固定且密封在海底,浮子用张紧的缆绳与发电机连接,并且采用直线电机为能量转化装置。美国于2008 年9 月成功对名为L-10 的振荡浮子式波浪能发电装置在俄勒冈纽波特进行了海试[4],其动力输出系统采用直线电机,额定装机10 kW。澳大利亚Carnegie Wave Energy 公司研制了一款“CETO”波浪能装置[5],采用大型水下浮子与安装海床上的涡轮泵组相连接发电。
对于振荡浮子式波浪能发电装置,国内外学者也一直在持续开展相关研究。Korde[6]通过在频域内对规则波作用下振荡浮子耦合振动系统进行了数值计算,研究了系统的近似最优电抗和电阻负载以及相应的捕获宽度比。Caska 等[7]对一种底部铰接在海底的圆柱浮子的水动力性能进行研究,利用了相对速度的莫里森方程,惯性力的系数通过辐射和绕射理论求解,用拖曳力系数模拟黏性效应,利用非线性公式计算浮子在规则波中的运动,得出了非线性拖曳力对浮子的运动性能影响很大的结论。
由于振荡浮子结构形状比较复杂,更多学者还是采用数值模拟开展研究。曹灿[8]应用AQWA软件系统研究了半径和质量对于圆柱浮子的水动力系数的影响,分析了不同角度的锥底浮子的水动力性能,并对锥底、圆柱、球底3 类浮子在规则波和不规则波中进行时域分析,对比研究浮子的各项水动力系数。周晨[9]应用OrcaFlex 软件建立了振荡浮子式波浪能发电机的运动模型,研究该装置的非线性水动力学特征,分析了在不同海洋工况下,装置浮子的运动性能变化,以及系泊结构的安全性是否得到保障;并对不同质量、电磁阻尼系数下浮子的振动效率进行对比研究,并根据基本公式计算了相应发电功率的数值结果。2018 年,周丙浩[10]基于AQWA 建立纵摇浮子的水动力模型,研究了半球底、锥底、台底3 种常见外形的浮子参数化的外形方案,分析了纵摇浮子在波浪中运动的水动力特性。Luan 等[11]通过STAR-CCM+建立了三维数值波浪水槽,模拟了单浮子在规则波中的相关问题,并得到了最优阻尼和波数之间的关系。
目前越来越多的学者也将目光投向多浮子阵列、双浮体装置耦合运动等复杂非线性问题的研究。清华大学刘秋林[12]利用线性势流理论下的频域和时域计算,分别在规则波和不规则波浪条件下对浮子阵列进行优化设计,计算其运动响应及波能捕获效率等。并将其俘能功率同单浮子结构进行对比,结果表明阵列装置能够更充分地利用波浪能资源,且在不规则波浪下,阵列中各浮子结构的俘获宽度比的差别小于规则波条件。杨绍辉等[13]采用数值模型研究了不同波向时浮子阵列被布置成圆周式、双列式和单列式3 种情况下的水动力响应特点以及浮子间距对各浮子波浪能吸收的影响。He 等[14]建立数值模型研究八角形平台和吸收式波浪能转化装置的水动力特性,并给出了相关平台的最终设计,研究发现多物体的相互作用对平台的能量吸收有较大影响。
随着物理模型试验模拟技术的提高,振荡浮子式波浪能发电装置这种复杂的海工结构也可以在物理模型试验中得以缩尺实现。Negri 等[15]在波浪水槽中测试了两个系统的物理模型,并使用单色波进行了测试。Ramadan 等[16]对一种用于波能转换的倒置杯浮子的改进设计进行了试验分析。结果表明,直径为30 cm、有挡板的浮子的捕集效率为19%,而直径为50 cm、没有挡板的浮子的捕集效率为6%。效率比常规设计提高了3 倍,且在规则波形作用下性能优越。对于波能转换器M4,Moreno 等[17]以1∶50 比例对6 浮子波能转换器M4 进行了物理模型试验。他们给出了在PTO 和系泊力处角运动的结果。采用不同谱峰和多向扩散的8 波条件,对11 个海上站点的发电量和电费进行了估算。然后,他们研究了波能转换器M4的多体线性衍射辐射模型,包括平均二阶力和辐射阻尼,以及平均激励力。通过对试验结果的比较,作者发现线性模型对所有波浪条件下的响应和运行时的功率捕获都给出了合理的预测,但所得到的二阶平均力只能对较小的[18]给出近似的预测。Santo 等[19]分析了位于西澳大利亚南海岸奥尔巴尼附近的M4 波浪能量转换器的性能,该地区以长期连续波浪而闻名。
本文采用势流理论建立了波浪与振荡浮子式桁架发电平台相互作用的数值模型,在时域内研究了振荡浮子式波浪能发电平台在波浪作用下的水动力特性,分析了水下浮子间距、浮子个数对浮子运动的影响,通过设置阻尼系数模拟液压缸对浮子运动的影响,找到了浮子的最佳发电阻尼。相关计算结果可以为形状相似振荡浮子式桁架波浪能发电平台设计提供数据参考。
1 数值方法
采用绕射理论开展波浪与结构物的相互作用问题研究。建立右手坐标系开展相关研究,在平台中心设置固定坐标系Oxyz,针对每个浮子,设置随体坐标系Oi′xi′yi′zi′,来描述每个浮子的运动,i表示第i个浮子,假设流体为理想流体,则存在速度势φ 在流域内满足拉普拉斯方程和相应的边界条件[20],平台模型图见图1。

图1 波浪和多浮子桁架式WEC 平台示意图Fig.1 Sketch of the wave and multi buoy truss-type WEC platform
平台和振荡浮子之间通过浮子臂和液压缸连接,如图2 所示。基于杠杆原理,当浮子承受较小的波浪力,可以推动后方的液压缸工作产生能量。因此,浮子受到的波浪力通过液压缸放大作用在平台上。每个浮子的运动方程如下:
式中:[M]为浮子和平台的质量矩阵;[B]为阻尼矩阵;[C]为恢复力矩阵;{F}为浮子和平台的受力情况,ξi和ξ0分别为各个浮子和平台的运动响应,Lri和Lli分别为浮子和平台的浮子臂长度。
2 数值模拟分析
2.1 两自由浮体模型
波浪与WEC 平台的研究实际上是一个多浮体相互作用问题。为了验证数值模型,采用自由双箱结构的线性波相互作用模型,如图3 所示。其中L,B,T和W分别表示方箱的长、宽、吃水和间距,d表示水深,具体尺寸及计算参数如表1 所示。方形箱体的质心位于箱体底部中心正上方2.56 m 处。
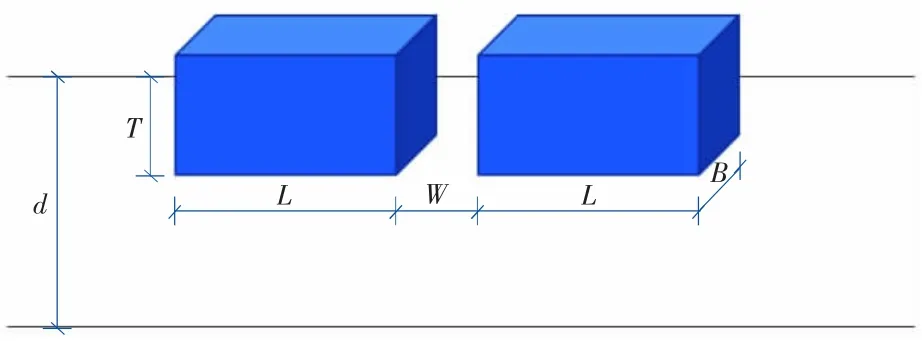
图3 两自由浮体与波浪相互作用示意图Fig.3 Sketch of interaction between twin-box and waves
2.2 模型验证
应用本模型计算波浪入射角为0°时的两自由方箱的水动力系数和运动响应。图4(a)、(b)为迎浪侧和背浪侧方箱纵摇方向的运动响应随波频的变化情况。图4 中将波浪力fx和运动响应ξ5进行无因次化处理,m、g、L、A、ω、k分别为方箱的质量、重力加速度、方箱长度、入射波波幅、入射波频率、入射波波数。
从图4 可以看出本模型的计算结果与Choi 等[21]的计算结果吻合较好,仅在个别频率存在一些差异,其原因可能Choi 的模型采用常数元计算,本文采用高阶元计算,因此本模型可以用于后续桁架式波浪能平台的水动力响应计算中。
3 WEC 装置水动力计算与分析
3.1 参数介绍
平台为正方形,其参数见表2,浮子下部为圆台,其参数见表3。

表2 平台参数Table 2 Parameters of the platform

表3 浮子参数Table 3 Parameters of the buoys
3.2 单边浮子数对运动响应的影响
为研究浮子个数对平台发电效率的影响,分别通过数值模拟开展单侧浮子为1~4 个时浮子在垂直方向的运动响应,计算示意图如图5 所示。
以fli(i=1,2,3,4)来表示左侧第i个浮子,以fri(i=1,2,3,4)来表示右侧第i个浮子。开展波浪沿浮子布置方向传播的数值模拟,波浪入射角度180°,即沿着图5 中x轴的负方向传播。
首先分析对比不同方向波浪作用下,单侧布置1 个浮子时,不同周期规则波作用下浮子垂直方向的运动响应RAO(单位波幅下的运动响应幅值),如图6 所示。从结果发现,当波浪沿浮子布置方向传播时,迎浪浮子运动响应大于背浪浮子运动响应,特别是短周期波浪作用时,由于平台对波浪有一定程度的反射作用,因此迎浪浮子运动更明显,波浪周期4 s 时,浮子受到垂直方向波浪力较小,因此垂直方向运动响应也较小。单个浮子的自振周期接近5.0 s,因此波浪周期T=5 s时由于共振现象升沉运动明显增加。而长周期波浪作用时,平台对波浪传播的影响变小,迎浪和背浪侧浮子运动趋于一致。
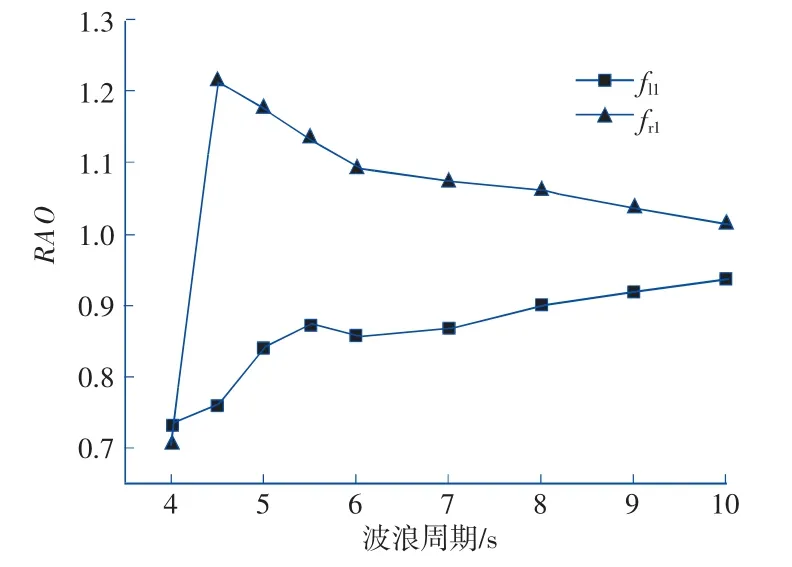
图6 不同周期波浪下浮子垂荡响应(单侧1 个浮子)Fig.6 Heave motion response of buoys in different wave periods(one buoy on one side)
随后分析单侧布置2 个浮子时计算结果,如图7 所示。当波浪沿浮子布置方向传播时计算结果与单浮子情况相似。
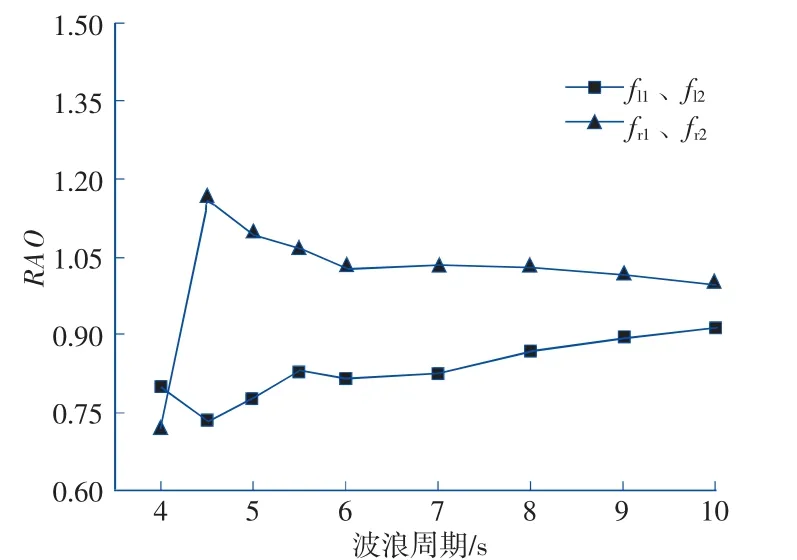
图7 不同周期波浪下浮子垂荡响应(单侧2 个浮子)Fig.7 Heave motion response of buoys in different wave periods(two buoys on one side)
进一步分析单侧布置3 浮子和4 浮子情况的计算结果,如图8、图9 所示。计算结果与之前相近,当波浪沿浮子布置方向传播时,两侧的浮子运动略大于中间的浮子运动,整体还是呈现迎浪侧浮子运动略大,背浪侧浮子运动略小,随着波浪周期的增大,运动响应趋于一致。

图9 不同周期波浪下浮子垂荡响应(单侧4 个浮子)Fig.9 Heave motion response of buoys in different wave periods(four buoys on one side)
综上整体来看,各个方向波浪作用下浮子运动响应差别不是特别大,同时各个浮子质量较轻,都有较好的随波性。但是浮子自身尺寸相对较大,波浪经过浮子时会发生绕射散射现象,迎浪侧浮子的运动响应略大于背浪侧浮子运动响应。
综合上述4 种情况,统筹考虑装置的发电效率和经济性,选择出最优浮子布置方式。由以上浮子的RAO计算结果可以计算得到,180°入射波浪条件下,浮子的RAO平均值如图10 所示。在大部分波浪周期下,单浮子布置情况下浮子的RAO为最大,且随着单边布置浮子数量的增多,浮子的平均RAO越小,当波浪周期大约为5 s 时,浮子的垂向运动幅值最大。说明在一定范围内,浮子的存在虽然对运动响应有影响,但由于浮子整体质量较小,而且浮子尺寸不是特别大,因此影响效果有限,浮子整体体现出非常好的随波性。因此,在条件允许情况下,尽可能多布置浮子可以有效提高平台的发电效率。

图10 不同波浪周期下平台各浮子平均的垂荡运动响应Fig.10 Average heave motion response of buoys on the platform in different wave periods
3.3 不同线性PTO 阻尼对装置捕获效率的影响
本装置中浮子通过浮子臂与平台相连,在波浪场中做垂荡运动,浮子臂末端通过杠杆原理推动PTO 动力输出装置,克服PTO 阻尼做功,这一部分所做的功才是装置发电系统利用于发电的能量。因此在发电系统捕获波浪能量的过程中,PTO 阻尼的大小对于能量捕获效率的影响非常显著。PTO 阻尼的大小能够改变浮子的垂荡运动响应以及运动速度,从而影响浮子对波浪能量的俘获,因此研究不同线性PTO 阻尼对装置捕获效率的影响尤为必要。在数值模拟中引入一个常数C作为阻尼系数,来调节阻尼力[22-23]。通过在不同线性阻尼系数C下对多浮子波浪能发电装置进行仿真模拟,探索不同的线性PTO 阻尼系数对捕获效率的影响。
用下面的方程来模拟PTO 系统中的阻尼力:
式中:v为浮子的升沉速度;C为线性阻尼系数,表示PTO 系统的性能。计算中,线性阻尼系数带入运动方程(1)中得到浮子对应的运动响应,进而得到阻尼力。
阻尼系数为C时浮子所俘获的波浪能量总功率为:
WEC 平台的能量捕获效率可表示为单波周期内浮子吸收的总能量(Ef2)与浮子宽度区域内波的总能量(Ef)之比,即:
数值模拟中,在单个浮子中加入升沉方向的线性阻尼系数。波沿浮子排列方向传播,当浮子平均RAO最大时,波幅为0.5 m,波周期为5 s。计算了浮子在升沉运动中的速度随时间的变化规律。不同线性阻尼系数C下的速度时程如图11 所示。结果表明:随着线性阻尼系数的增大,浮子的速度明显减小。

图11 不同线性阻尼系数C 的浮子速度时程Fig.11 Velocity time histories of the buoy with different linear damping coefficients C
进一步计算不同线性PTO 阻尼系数C下浮子最大捕捉波能的功率P和浮子的能量捕获效率ηf,如图12 所示。

图12 不同线性PTO 阻尼下浮子的发电功率和捕获效率Fig.12 Generation power and capture efficiency of buoy under different linear PTO damping coefficients
随着线性阻尼系数C的增大,浮子的捕获效率先增大后减小,当C=30 000 N/(m·s-1) 时捕获效率达到最大值,由此得出C=30 000 N/(m·s-1)为WEC 平台的最优PTO 阻尼系数。进一步得到WEC 平台各浮子的捕获效率,如表4 所示。
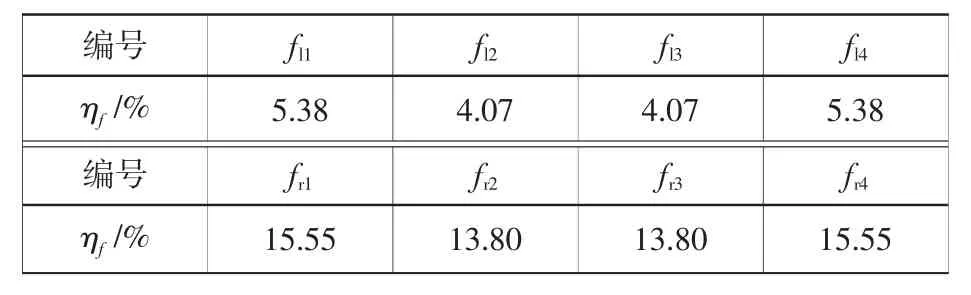
表4 每个浮子的捕获效率Table 4 Capture efficiency of each buoy
4 结语
本文基于势流理论,采用高阶边界元方法建立了波浪与波浪能发电平台相互作用的数学模型,研究了多浮子式波浪能平台各个浮子的运动响应,分析了浮子个数,浮子布置方式对浮子运动的影响,通过线性阻尼模拟液压缸对浮子的作用进而做功发电,达到对多浮子波浪能发电装置进行仿真模拟的目的,得到如下结论:
1) 各个方向波浪作用下浮子的运动响应差别不大,各个浮子都有较好的随波性。迎浪侧浮子的运动响应略大于背浪侧浮子的运动响应,一侧浮子中两边浮子的运动响应略大于中间浮子的运动响应。
2) 随着单边布置浮子数量的增多,浮子的平均RAO变小,但是差别较小,多浮子整体体现出非常好的随波性。因此,在条件允许情况下,尽可能多布置浮子可以有效提高平台的发电效率。
3) 在某一周期波浪作用下,单个浮子的发电功率和效率随着线性阻尼的增大而先增大后减小,当阻尼为30 000 N/(m·s-1)时,发电效率最高,单个浮子最大捕获效率为15.55%,浮子的平均捕获效率为9.7%。

