On-the-Fly Nonadiabatic Dynamics of Caffeic Acid Sunscreen Compound

Xu Kang,Yifei Zhu,Juanjuan Zhang,Chao Xu,Zhenggang Lan

SCNU Environmental Research Institute,Guangdong Provincial Key Laboratory of Chemical Pollution and Environmental Safety.and MOE Key Laboratory of Environmental Theoretical Chemistry,School of Environment,South China Normal University,Guangzhou 510006,China

As a widely-used sunscreen compound,the caffeic acid (CA) shows the strong UV absorption,while the photoinduced reaction mechanisms behind its photoprotection ability are not fully understood.We try to investigate the photoinduced internal conversion dynamics of CA in order to explore the photoprotection mechanism.The most stable CA isomer is selected to examine its nonadiabatic dynamics using the on-the-fly surface hopping simulations at the semiempirical level of electronic-structure theory.The dynamics starting from different electronic states are simulated to explore the dependence of the photoinduced reaction channels on the excitation wavelengths.Several S1/S0 conical intersections,driven by the H-atom detachments and the ring deformations,have been found to be responsible for the nonadiabatic decay of the CA.The simulation results show that the branching ratios towards these intersections are modified by the light with different excitation energies.This provides the valuable information for the understanding of the photoprotection mechanism of the CA compound.

Key words: Caffeic acid,Nonadiabatic dynamics,Surface hopping

I.INTRODUCTION

Excessive solar radiation is harmful to human skin cells,because sunlight contains significant amounts of ultraviolet (UV) radiation that may cause serious skin diseases [1,2].Sunscreen compounds can effectively protect the skin from UV damage [3-6],which are widely used in daily life.Sunscreen compounds can be divided into two main categories according to their source,natural sunscreen compounds and artificial sunscreen compounds [3-5].It is rather important to explore their complex photoinduced reaction processes at the molecular level,in order to understand their photoprotection mechanism and to provide the useful hints for the design of commercial sunscreen compounds.In recent years,some sunscreens and their degradation products have been reported to be harmful to humans and environment [7,8].This further increases the necessity to clarify the photodegradation products of sunscreen compounds.

Many sunscreen organic molecules,such as caffeic acid (CA) [9-11],ferulic acid (FA) [9,12-14],sinapic acid (SA) [15-18],methyl sinapate (MS) [19-21],sinapoyl malate (SM) [15-17,22],andetc.[3-5,23-25],contain aromatic rings conjugated to carbonyl groups.These compounds received the considerable research attentions from both experimental and theoretical views[9-22].Several works tried to clarify what are the essential factors that can modify the performance of sunscreen compounds,which focused on the structureproperty relationships,the substitution effects [5,26,27],the solvent effects [5,27,28] and the pH-value [5,13,15,29] influences.These works showed that (i) a very complicated mechanism may exist in the photoreaction of these sunscreen molecules,(ii) the photodynamics mechanism may be highly dependent on the individual systems and surrounding environments,and(iii) different influence factors may strongly interplay with each other.For instance,the ethylhexyl methoxycinnamate (EHMC) [27,28] in the gas phase shows the rather long excited-state lifetime,while the EHMC-water cluster displays much faster excited state population decay.In addition,even the non-polar solvent (such as cyclohexane) can accelerate the decay dynamics of EHMC with respect to its counterpart in the gas phase.Similarly,it was demonstrated that the excited-state dynamics of the cinnamates is deeply influenced by the solvent environments [5,24].As the contrast,the significant solvent effects do not seem to exist in the photoinduced dynamics of meradimate [26].

As several functional groups co-exist in sunscreen compounds,each may associate with a conical intersection (CI) and all of them may be involved in the nonadiabatic dynamics.Taking several well-known cinnamate derivatives (CA,FA,SA and MS) as typical examples,all of them contain the aromatic ring,-OH group,C=O group,and C=C double bond,as shown inFIG.1.Here CA has two-OH groups in the six-member ring,FA has one-OH group and one-OCH3group,SA has one-OH group and two-OCH3groups,and MS is built from SA by replacing the-OH of the-COOH group with the-OCH3group.As the consequence,several relevant conical intersections may be responsible for the nonadiabatic dynamics of these compounds.The first possible decay channel is governed by the well-knownπσ∗-driven H dissociation [3-5,24],and the similar channel was well studied in phenol and its derivates [30-35].The second possible channel is governed by the deformation of the aromatic ring [3-5,24],and such out-of-plane ring deformations widely exist in the photochemistry of the DNA bases [36-38].The third channel is driven by the photoinduced isomerization at the C=C double bond [3-5,24],which is a typical photoinduced reaction in the C=C conjugated systems [39].The forth channel is controlled by the intramolecular excitedstate hydrogen transfer in the case of the presence of the intramolecular hydrogen bonds [3-5,24,40],and such type of motions widely exist in biomolecular mimic systems [41].Due to the existence of the C=O bond,the darknπ∗state may be involved in photochemistry [3].This even gives the possibility to induce the intersystem crossing [3-5].In one word,one of the most challenging problems in the study of the photoreaction mechanism of sunscreen compounds is that many reaction channels may appear simultaneously,while the role of these involved conical intersections may be dependent on the molecular structures of sunscreen compounds and their ratio is easily modified by the introduction of other functional groups.For instance,previous works proposed that the nonadiabatic decays of CA and FA might be governed by the O-H bond fission or other ring-distortion conical-intersection (CI) channels[42],while the SA and SM were assumed to experience the ultrafasttrans-cisphotoisomerization in the solutions [17].In addition,some of these channels may be easily influenced by the solvent environments,such as solvent polarity and viscosity [3-5,23,25],while other channels may not.This enhances the complexity in the study of the photoprotection mechanism of sunscreen compounds.More detailed discussions on the nonadiabatic dynamics of sunscreen compounds are found in several excellent reviews [3-5,24].

Several sunscreen compounds (CA,FA,SA,SM,and MS) share many geometrical similarities,as discussed above.There were many intensive studies on SA and SM [15-18,22],and the nonadiabatic dynamics simulation on the FA was also available [12].For instance,Caoet al.proposed that the internal conversion of the FA molecule follows the two-step mechanism,in which both six-member ring puckering distortion motion and the bridged C=C double bond twisting motions are involed [12].However,much less studies were conducted for CA [9-11] and thus we selected the CA as the typical example to examine its nonadiabatic dynamics in this work.

In theoretical point of view,the direct simulation of the nonadiabatic dynamics is helpful to clarify the photoprotection mechanism of sunscreen compounds [12,40].According to the previous work by Karsiliet al.,three possible CIs may be relevant to the photochemistry of CA,which are governed by the out-of-plane ring deformation,the H-atom dissociation,and the C=C double bond twist [42].Therefore,the current nonadiabatic dynamics simulation helps us to know the role of each involved CI in the excited-state reactions of the CA.

Herein,we employed the on-the-fly trajectory surface hopping dynamics to simulate the photoinduced nonadiabatic dynamics of caffeic acid (CA).Due to the large size of the CA molecule,the electronic-structure calculation in the on-the-fly surface hopping dynamics was preformed within the orthogonalization-corrected model (OM2) Hamiltonian in the combination with multireference configuration interaction (MRCI) treatment.Several previous studies demonstrated that the OM2/MRCI level can provide the reasonable description on the excited-states processes of various molecules with the rather low computational efforts [43-46].Several CIs are located and their roles in the nonadiabatic dynamics of the CA are addressed.Their contributions under different excitation wavelengths are discussed.The current work provides the essential understandings of the photochemistry of CA,giving the valuable information for clarifying the photoprotection mechanism of many sunscreen compounds with geometries similar to CA.

II.COMPUTATIONAL DETAILS

We first optimized the geometries of 12 isomers of the CA molecule at the OM2/MRCI [47,48] level.Among them,the most stable isomer with the lowest ground-state energy was chosen as the target compound,and the information of all isomers is given in FIG.S1 in Supplementary materials.

All electronic-structure calculations were performed at the OM2/MRCI level.The molecular orbitals were generated by the restricted open-shell Hartree-Fock(ROHF) approach.Three references (the close-shell configuration,the single and double HOMO-LUMO transitions) were used to build the configuration interaction expansion.The active space AS(12,11) was chosen to distribute 12 electrons in 11 orbitals including fourπ,twon,twoσ∗and threeπ∗orbitals,and these orbitals are given in FIG.S2 in Supplementary materials.To examine the dependence of the simulation results on the selection of the active space in the OM2/MRCI calculations,additional calculations with the large active space AS(14,12) were also taken to rerun all simulations.The minimum-energy CI structures were obtained by the CI optimization using the Lagrange-Newton method [49].

We validated the OM2/MRCI accuracy by providing additional electronic structure calculation results at the high-correlated levels.We tried to perform the optimization of all critical geometries,including excitedstate minima and relevant conical intersections at the XMS-CASPT2/cc-pVDZ level with the active space (8,7) including one n,threeπand threeπ∗orbitals,as shown in FIG.S3 in Supplementary materials.Here the XMS-CASPT2 calculations were preformed with the BAGEL package [50].

The nonadiabatic dynamics was simulated by on-thefly surface hopping method.The nuclear initial conditions (atomic coordinates and momenta) in the dynamics simulations were sampled according to the Wigner distribution [51] function of the lowest vibrational level at the electronic ground state.More additional discussions on the initial samplings are given in Supplementary materials.We next vertically placed these initial conditions to three lowest excited singlet excited states(S1,S2,and S3) to initialize the dynamics propagation.The time step of 0.5 fs was chosen for the nuclear propagation,and 100 steps of the electronic motion were calculated in each step of the nuclear evolution.All quantities in the nonadiabatic dynamics simulations such as energies,gradients,and nonadiabatic coupling vectors,were computed at the OM2/MRCI level using the MNDO package [52].More details on the calculation of nonadiabatic couplings can be found in Supplementary materials.We employed the Tully’s fewest switches algorithm to describe the nonadiabatic transitions [53].The decoherent correction proposed by Granucci and Persico was employed and the relevant parameter was set to 0.1 Hartree [54].At hops,the velocity rescaling was performed to satisfy the energy conservation,which was adjusted according to the orientation of the nonadiabatic coupling vector.For frustrated hops,the velocity component along the nonadiabatic coupling vector was reversed.All dynamics calculations were performed with the JADE-NAMD package [55-57].Finally the results were obtained by the average of 189,175,and 165 trajectories for the dynamics from S1,S2,and S3,respectively.

One of the important issues is how to compute the branching ratio of all channels under the different excitation wavelengths.In fact,this is a rather critical issue in the theoretical description of the photochemistry and more detailed discussions were clearly given in previous works [58-60].Here we took a rather practical approach.In each energy window,the probability toward each reaction channel was estimated by the destination of trajectory starting from such window,weighted by their initial transition probability [58].More technical details are given in Supplementary materials.

III.RESULTS

In this work,the surface hopping dynamics was investigated by using the OM2/MRCI method with two different active spaces,AS(12,11) and AS(14,12).Since both give the very similar data,we mainly report the results obtained with the AS(12,11) and put simulation data with AS(14,12) into FIG.S5 and Table S1 in Supplementary materials for comparison.Such similarity gives us the confidence that the current selection of the active space is reasonable.

A.Electronic-structure calculations

Totally 12 isomers were optimized on the ground state,which are mainly differed by the orientation of two-OH groups,and the rotation statuses of the C3-C10bond and C10=C12double bond.Among them,the most stable isomer with the lowest ground state energy was selected to study its photochemistry,whose structure is shown inFIG.2(a) and FIG.S1 (a) in Supplementary materials.The most stable isomer is consistent with previous findings [42].For this isomer,we optimized the S0-min,S1-min (as shown inFIG.2),S2-min,S3-min (FIG.S6 in Supplementary materials),and all involved CIs.The key geometrical parameters of several important geometries are displayed in Table I.

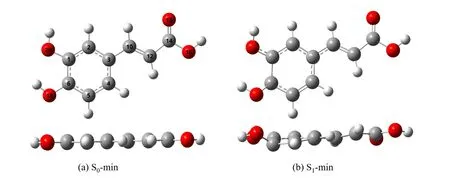
FIG.2 The structures of (a) S0-min and (b) S1-min with differnt views.

The most stable isomer at the ground state is shown inFIG.2(a).The bond lengths of O20-H,O18-H,C3-C10,C10-C12are 0.992 Å,0.996 Å,1.457 Å,1.353 Å,respectively,and the dihedral angles of C2-C3-C10-C12and C3-C10-C12-C14are both 180°.All atoms are located in the same plane.Two H atoms of the-OH groups attach to the ring lie in the same side,and the direction of the meta-O20H group points away from the molecular center.The hydrogen bonding interaction exists between the H atom of thepara-O18H group and the O atom inmeta-O20H group with the distance of 2.168 Å.This result is very similar to the data in previous work [42].

TABLE I Key geometrical parameters (bond lengths in Å and angles in degree) of the S0-min,S1-min and four CIs at the OM2/MRCI level,together with the S0-min results reported in the previous work [42].

At the S 0-min,three lowest singlet excited states (S1,S2and S3) display theππ∗,ππ∗,andnπ∗characters with the excitation energies of 4.28 eV,4.71 eV,5.18 eV,as shown inFIG.3.The choice of active space has no significant effect on the results,see Table S2 in Supplementary materials.The electronic absorption spectrum of caffeic acid in water solution [61] shows absorption bands at 312 nm and 287 nm (3.97 eV and 4.32 eV).In the present work,the vertical excited energy of bright S1and S2state is 4.28 eV and 4.71 eV,respectively.The results are systematically higher than those in the experiments.Similar features were found in previous CASPT2 calculations [42].

FIG.3 Electronic transitions and excitation energies of the low-lying electronic states at S0-min at the OM2/MRCI level.

Different from the planar geometry of the S0-min,the S1-min displays a distorted geometry.At the S1-min,the most significant geometrical feature is the twisting motion of the C3-C10bond,from 180.0° at S0-min to 168.0° at S1-min,as shown inFIG.2(b).In addition,the weak ring deformation also takes place at the S1-min.

Four S1/S0CIs shown inFIG.4are obtained by the CI optimization,which are differed by the stretching motions of the O-H bond (FIG.4(a) and (b)) and the out-of-plane distortion of benzene ring (FIG.4(c) and(d)).The energy levels of these CIs (CI-I to CI-IV) are shown inFIG.5.For all S1/S0CIs,their energies are in the range of 3.54 eV to 3.84 eV,which are less than the vertical excitation energy of the S1state at the S0-min.In principle,all of them may be accessible in photoinduecd reactions.

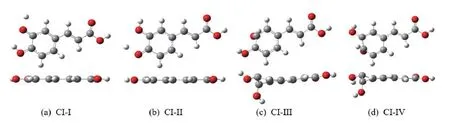
FIG.4 The optimized structures of S1/S0 CIs structures,(a) CI-I,(b) CI-II,(c) CI-III,and (d) CI-IV,at the OM2/MRCI level.

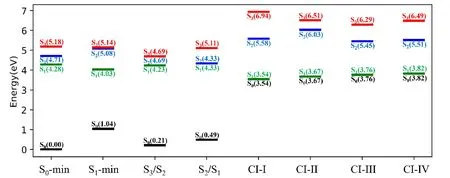
FIG.5 The energy level diagram of electronic states at important geometries including S0-min,S1-min,S3/S2 CI,S2/S1 CI,CI-I,CI-II,CI-III,and CI-IV at the OM2/MRCI level.

The first CI (πσ∗/S0,CI-I inFIG.4(a)) lies at 3.54 eV,which is characterized by the pronouncedmeta-O20H stretching motion upto 1.549 Å.The positions of other atoms show no significant alternation,and the molecule still maintains the planar structure.The second CI (πσ∗/S0,CI-II inFIG.4(b)) at 3.67 eV also shows the OH stretching motion and the whole compound remains the planar structure.Here instead of the O20-H bond,the O18-H elongation was observed,which rises upto 1.538 Å.At the third CI (ππ∗/S0,CIIII inFIG.4(c)) at 3.76 eV,the meta-C1atom shows the large deformation out of the benzene ring plane,accompanied with the strong displacement of themeta-O20H group.At the forth CI (ππ∗/S0,CI-IV inFIG.4(d)) at 3.82 eV,thepara-C6 atom and thepara-O18H group display the strong deformation from the ring plane.

In addition,six additional optimized CIs do not play a major role in the nonadiabatic dynamics of CA,so their structures are presented in FIG.S7 of Supplementary materials.The CIs between different excited states,S3/S2and S2/S1,at the Franck-Condon region were also located,as shown inFIG.5and FIG.S8 in Supplementary materials.

For all important conical intersections,CI-I to CIIV,their geometries at the OM2/MRCI levels are not far from their corresponding structures at the XMSCASPT2 level,see FIG.S9 and Table S3 in Supplementary materials.For CI-I and CI-II,we always obtain the conical intersections that are characterized by the Hdissociation,while the whole ring remains planar.For CI-III and CI-IV,the geometries at the XMS-CASPT2 also show the similar deformation of the corresponding C atom,while some slight difference exists in the positions of some H atoms.Thus,the CIs obtained at the OM2/MRCI level are basically consistent with respect to the CIs obtained at high level of theory.Therefore,the current OM2/MRCI simulations can provide the qualitative understanding for the CA photochemistry.

B.Nonadiabatic dynamics

In the present work,the nonadiabatic dynamics starting from three lowest excited states were considered.In all cases,the ultrafast decays to the ground state are observed.Here about 50 % population reaches the ground state at 373 fs,346 fs,259 fs,when the dynamics start from S1,S2and S3states,respectively.Up to 1 ps,the internal conversion dynamics is essentially over,as shown inFIG.6.It is clear that the population decays to the ground state become faster,when the dynamics start from a higher energy excited state.

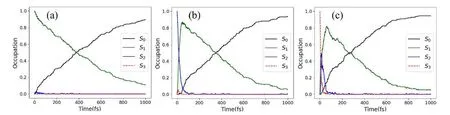
FIG.6 Time-dependent average fractional occupations of adiabatic electronic states in the nonadiabatic dynamics: (a) initiated from S1,(b) initiated from S2,(c) initiated from S3.

TABLE II The branching ratio of each CI channel in the nonadiabatic dynamics of CA.

By comparing the geometry similarities between the hopping structures and the optimized CIs,we may assign the nonadiabatic decay channels approximately in Table II.More additional assignment details are given in Supplementary materials.At the same time,we examined the dependence of the ratio of reaction channels on the excited energy,and four intervals are defined:<4.1 eV,4.1-4.5 eV,4.5-5.0 eV,and >5.0 eV.The branching ratios towards each channel at different excitation wavelengths are displayed in histogram inFIG.7(a).As discussed above,the reaction probability of each channel was estimated by the destination of trajectory starting from each energy window,weighted by their initial transition probability [58].

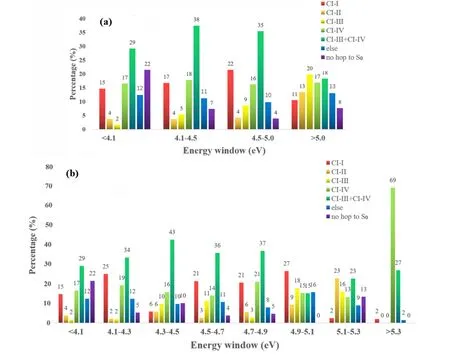
FIG.7 The branching ratio of the photoreaction channels under different excitation energies: (a) four domains including<4.1 eV,4.1-4.5 eV,4.5-5.0 eV,and >5.0 eV,respectively;(b) eight energy domains including <4.1 eV,4.1-4.3 eV,4.3-4.5 eV,4.5-4.7 eV,4.7-4.9 eV,4.9-5.1 eV,5.1-5.3 eV,and >5.3 eV,respectively.

Next,we tried to examine the contribution of each ring deformation channel (CI-III,CI-IV,and CI-III+CIIV).Among them,the mixing channel is always important in all initial conditions.In addition,the contribution of this channel first increases and then decreases with the higher energy,which is,29% (<4.1 eV),38%(4.1-4.5 eV),35% (4.5-5.0 eV),and 18% (>5.0 eV).The secondary ring deformation channel is the pure CI-IV channel,whose ratio remains rather stable (about 17%)in all energy windows.The pure CI-III channel plays the very minor role in the low energy domain while its contribution increases significantly in the high-energy domain.

The hydrogen dissociation channels via CI-I and CIII are also important.Their total contribution reaches 24%,21%,and 27% for the dynamics from S1,S2and S3,respectively.In energy window,their branching ratio are 19% (<4.1 eV),21% (4.1 eV-4.5 eV),26%(4.5 eV-5.0 eV),24% (>5.0 eV),as shown inFIG.7(a).Among them,the CI-I channel is the leading one and the CI-II is the minor one.The contribution of the former channel increases up to 22% as the excitation wavelength becomes shorter,while its component decreases if the energy rises more than 5.0 eV.As a contrast,the ratio towards the minor CI-II channel increases monotonically by increasing the excitation energy.

Several hopping geometries display the similar structures in the ring moiety part,while the side chain shows different configurations.For instance,in the out-of-motion ring deformation channel,some hopping geometries show the twisting motion at the side chain,and the C 3-C 10 bond torsional motion is involved.The underline reason is that the involved CIs have a very flat seam along the corresponding twisting motion,as shown in FIG.S10 in Supplementary materials.This indicates that the C3-C10twisting motion is not the leading motion,although it is involved.

As shown inFIG.7,other channels may appear and some highly distorted molecular geometries may appear.As their contributions are rather minor in all chosen energy domains (about 10%),we do not discuss them here.It is worthwhile to mention that only one or two trajectories show the twisting motion at the side of C=C double bond,and this seems to indicate that such motion is not important at all in the nonadiabatic dynamics of CA.

As a short summary,when the low energy excitation is considered,the primary channel is governed by the ring deformation,while the secondary channel is driven by the hydrogen dissociation.However,with the very high excitation energy,all channels become equally important.

The linearly-interpolated reaction pathways were constructed to explain the branching ratio toward these channels.As shown inFIG.8,the barrier of the system from S1-min to CIs are 0.66 eV,0.94 eV,1.13 eV,and 0.46 eV for the CI-I,CI-II,CI-III,and CI-IV channels,respectively.

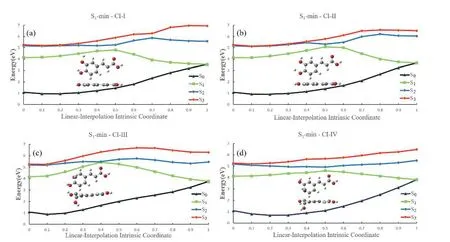
FIG.8 Linear interpolated potential energy surfaces between S1-min and S1/S0 CIs at the OM2/MRCI level.

Clearly the reaction barrier towards the CI-IV is the lowest one,therefore,this channel becomes dominant in almost all excitation situations (2.9-5.3 eV),if we sum all trajectories displaying the purely CI-IV feature and the CI-III+CI-IV feature.Furthermore,the pathway towards CI-III displays the highest barrier,thus this channel plays a very minor role in the low excitation energy domain (<5.0 eV).For the hydrogen dissociation channels,the barrier towards CI-I is lower than that towards CI-II.Therefore,more trajectories pass the former one when the excitation energy is not very high(<5.0 eV),as given inFIG.7.The underline reason to cause the different features for two hydrogen dissociation channels is possibly due to the existence of the intramolecular hydrogen bond between the H atom in thepara-O18H group and the O atom in themeta-O20H group,which prevents the corresponding H-atom dissociation.

When the initial excitation energy is very high(>5.0 eV),the system should have enough energy to overcome barriers of all channels.As the consequence,all channels are open with the similar contributions in the high energy domain (>5.0 eV).

Herein,the reaction probability of the CI-II channel is lower than that of CI-III channel,while the energy barrier of CI-III is higher than that of CI-II.The linearinterpolated pathways that connect S1-min and the relevant CIs only provide a very approximated view on the potential energy profiles towards the relevant CI channels.In addition,such a pathway is also dependent on the chosen coordinates.When different internal coordinates are employed,we may get different profiles.In this sense,we cannot only reply on these data to give very precise discussion on the importance of each channel,particularly for the energy with high barrier.

The CI-II channel provides a H-atom dissociation pathway.In the real dissociation,the motion of the H atom may be very flexible and it is easy to interact with the O atom of neighboring OH group to form the hydrogen bond.This may reduce the H-atom dissociation probability governed by the CI-II channel.

FIG.7(b) provides an additional result with more intervals in energy windows.It is clear that the key dynamic features are consistent with the results inFIG.7(a).For example,the CI-III +CI-IV mixing channel is always dominant in the low-energy situations.For the H dissociation channel,the proportion of CI-I is always more than that of CI-II when the energy is not very high.In the low energy domain,the proportion of CI-II and CI-III is very small.All channels are open in the high energy domain (>4.9 eV).We wish to emphasize that the oscillator strengths are all very small for the initial conditions above 5.0 eV.As we considered the transition probabilities as the weight of each trajectory in the calculations of the final branching ratio,the results are very sensitive here by adding or deleting some trajectories.Therefore,we can only roughly say that all channels are open here.

IV.DISCUSSION

The current simulation was performed by using the semi-empirical OM2/MRCI [47,48] method to perform all dynamics simulation,mainly to save the computational cost.The surface hopping dynamics calculations of the same system with the highly-level correlated theories,such as complete active space self-consistent field(CASSCF) [62,63] and multi-configurational second order perturbation theory (CASPT2) [64] levels,are rather time consuming,unless the very small active space is used.If the nonadiabatic surface hopping dynamics simulation employs the single-reference levels,such as the standard linear-response time-dependent density-functional theory (TD-DFT) [65],we suffer from the improper description of the double-cone topology of the S1/ S0conical intersection [66].Therefore,we decide to take the OM2/MRCI method in the nonadiabatic dynamics,since many previous works demonstrated that this method may provide the reasonable results with the manageable computational costs [43-46].One additional advantage of the OM2/MRCI method is that the dynamics under different active space remains very similar to each other.This indicates that the current results obtained by the OM2/MRCI method is rather robust,see Supplementary materials.

In some sense,our results are still qualitatively reasonable,although the OM2/MRCI method is employed.For instance,this method correctly predicts the structure of the most stable isomer,which is highly consistent with the previous high-level electronic structure calculations [42].At the same time,the previous work[42] clearly demonstrated that the ring deformation may exist in the low-energy excitation,the H atom in the-OH group dissociation may experience some barrier and thus it appears on the high-energy excitation situations.It is also shown that the double-bond twisting may not be involved in the CA photochemistry.In the current work,we find the similar features,although some details are different.

There are two-OH groups,i.e.,themeta-O20H andpara-O18H groups.The previous work [42] found that the hydrogen dissociation may take place in themeta-O20H group and did not discuss the second hydrogen dissociation channel relevant to thepara-O18H group.In our work,we find that the former channel takes place much more easily than the second one.For the ring deformation channel,the previous work [42] found that thepara-O18H group is involved in this pathway.In our work,we also find that thepara-O18H group is essential in the ring deformation channel,while the ring puckering motion associated with themeta-O20H group seems less important.At the same time,our dynamics simulation find that the twisting motion at the side C=C double bond does not seem to be important at all.In this sense,the critical CIs found in the previous work[42] are identified as the important channels,while all other CI channels not reported by the previous work[42] are classified as the minor ones by our work.In this sense,our work provides the qualitatively reasonable results to explain the nonadiabatic dynamics of CA.

In the current surface hopping simulation,we find that the the time of the half trajectories decaying to the ground state of the excited state of the CA compound is nearly 250-400 fs.The close examination of the involved decay channels indicates that two groups of trajectories give different decay time scales,which are<100 fs for the H-atom dissociation channels and∼500fs for the ring deformation channels.In the timeresolved spectroscopic studies of the CA [9],three time constants were given.Here we tried to provide some possible explanations on their findings according to our current simulations.The H-atom dissociation channel always takes place quickly (<100 fs),which may correspond to the shortest decay time constant (τ1<100 fs) in the CH3CN and dioxane solutions.The second decay time constantτ2with several hundred fs up to near 1 ps may be attributed to the nonadiabatic dynamics following the ring deformation CI channel.The last channel with the longest time scaleτ3may be relevant to the solvent reorganization that generally takes place in the long time scale.Here our simulations do not observe the deep involvement of the C=C double bond twisting motion.In addition,from CA to FA,themeta-O20H group is replaced by the-OCH3group.As the H-atom dissociation channel is more relevant to themeta-O20H group,such replacement leads to the vanishing of the corresponding channel.This may explain why the shortest time scaleτ1becomes much longer in FA.Certainly,the above assignment only represents our initial preliminary understanding on the experimental findings.More additional works should be performed to clarify the reliability of this assignment.

However,we fully acknowledge that the OM2/MRCI method is a semi-empirical method and our results are highly approximated.We can easily pick up some possible deficiencies in our simulations.For instance,the current calculations show that the low-lyingS1state is aππ∗state,consistent with the previous work[42].However,for two states that are not far from each other (S2and S3),we obtain different states ordering at the OM2/MRCI level with respect to the previous work[42].In addition,our results show that one of the-OH group dissociation channels and one of the ring deformation channels exist even in the low-energy excitation,giving the short time of the half trajectories decaying to the ground state of the CA.This seems to be contradictory with the conclusions of the high-level electronic structure calculations [42].This indicates that the current method may underestimate the energy barrier on the excited state,giving the higher chance to induce the photoreactions.Certainly,the additional experimental and theoretical works are necessary to give more information on the detailed reaction mechanism.It should be an important research topic in the future.

V.CONCLUSION

In the current work,we tried to study the photoinduced reactions of the sunscreen compound caffeic acid(CA) for the understanding of its photoprotection mechanism.The nonadiabatic dynamics of the most stable isomer of the CA was simulated by the on-the-fly trajectory surface hopping dynamics at the semi-empirical OM2/MRCI level.Several CIs are located,which are responsible for the nonadiabatic dynamics of the CA compound.Particularly,the branching ratio towards different reaction channels under the photoexcitations with different excitation wavelengths was discussed.

In the current simulations,two groups of CIs are found to dominate the excited-state decay of CA molecule.The first group of CIs is governed by the hydrogen dissociation.This process may generate free radicals that can be harmful to the human body and the environment.Although two-OH groups exist here,the hydrogen dissociation takes place more easily in themeta-O20H group,instead of thepara-O18H group.The second type of CIs is governed by the puckering deformation of the six-member ring,which shows the strong out-of-plane motion of the ring moiety.These channels are involved in the nonadiabatic dynamics of the CA in all situations.Although we also find other CIs,they do not play important roles here.

The ratio of all channels are clearly modified by the light excitation wavelengths.At the long wavelength region,the channels with lower barriers dominate the dynamics.In this case,the ring deformation CI seems to be the major one and the hydrogen dissociation is the secondary one.Here the ring deformation at thepara-C6site and the hydrogen dissociation at themeta-O20H group may be the leading channel.The hydrogen dissociation at thepara-O18H group may be the secondary channel.With the increasing of the excitation photon energy,all of these channels start to play roles here.

The present work provides the useful information to explain the photoinduced dynamics mechanism of the CA molecule,which are valuable to understand the photoprotection mechanism of the related sunscreen compounds.In the theoretical studies of sunscreen compounds,it is clearly important to improve the simulation accuracy and describe more realistic working situations.In this sense,the employment of the high-level electronic structure methods in the nonadiabatic dynamics simulations or the inclusion of the solvent effects within the QM/MM frameworks may become the essential research topic in the future.

Supplementary materials:The isomers of caffeic acid(CA) and corresponding energies,active orbitals at the OM2/MRCI level and XMS-CASPT2 level,the results at high calculation level,all relevant geometries and their energies,CI-IV seam along the C2-C3-C10-C12torsional coordinate,additional results when the larger active space is used,vertical excitation energies with different active spaces,the branching ratio in the case that the high-frequency vibration modes are frozen in the initial samplings,the Cartesian coordinates of all important geometries,are all available.

VI.ACKNOWLEDGMENTS

This work was supported by the National Natural Science Foundation of China (No.21873112,No.21933011,and No.21903030).