车用锂离子电池健康状态估计

胡慧敏，庞知非

车用锂离子电池健康状态估计

胡慧敏1,2，庞知非1

（1.中华人民共和国交通运输部 运输车辆运行安全技术交通行业重点实验室，北京 100736； 2.长安大学 汽车学院，陕西 西安 710064）

锂离子电池作为新能源汽车的主要动力来源，其健康状态估计和电池的保养、维护与更换息息相关。文章选择电池容量作为直接健康因子，基于电池充电电压曲线提取3个间接健康因子，采用Pearson和Spearman相关系数计算其与容量之间的相关性。结果发现，等电压上升充电时间与容量的相关性最大，选取高斯过程回归（GPR）算法建立电池健康状态（SOH）估计模型，选用共轭梯度法（CGM）计算模型超参数，能够对锂离子电池SOH进行较好的估计。

车用锂电池；SOH；健康因子；高斯过程回归

据公安部统计，截至2022年底，全国新能源汽车保有量达到1 310万辆，较2021年同比增长61.73%，呈高速增长趋势。新能源汽车的动力电池种类包括镍镉电池、铅酸电池、磷酸铁锂电池和锂电池，其中，锂电池因具备相同储电量下体积更小、质量更轻、寿命更长，以及污染更小等优点，成为各大汽车企业的研究热点。电池健康状态（State Of Health, SOH）是电池当前的性能参数（如剩余电量、容量、内阻）与电池出厂时标称值的比值，其会随着使用时间的延长而减小。车辆运行时需要及时对SOH进行估算，以便于车主掌握电池的使用情况，在必要时可更换电池，减少不必要的经济损失和安全事故。

SOH估计方法种类繁多，主要有直接放电法、电化学模型、等效电路模型、数据驱动法，具体分析如下：

1）直接放电法是在特定情况下，将电池以恒定功率放电直到规定的电压，计算电池容量与电池出场容量比，得到电池SOH，该方法准确率高，但放电时间较长，不适用于在线测试，不便于车主使用车辆。

2）电化学模型将离子运动、反应热、电极材料变化等因素考虑在内，建立电池模型，对电池性能进行评估。该模型涉及多个参数，但电池老化的动态因素不便于模拟，且电化学反应差异较大，该模型的缺点是普适性不强。

3）等效电路模型是将电池等效为一个简单的电路，利用电路中的部分电子元器件对电池性能进行估计，该模型比较容易构建，计算过程也简便很多，但估计效果比不上电化学模型。

4）数据驱动法是将电池的电流、电压、电阻等这些采集到的历史数据输入到神经网络（Neural Network, NN）、支持向量回归（Support Vector Reg- ression, SVR）、高斯过程回归（Gaussian Process Regression, GPR）等模型中，估算出电池的SOH，也是近年来较为热门的研究方法之一。

YOU等[1]选择NN作为计算模型，电流、电压、温度作为计算数据来估算SOH。李刚等[2]选择NN作为计算模型，利用模糊预测优化模型，放电能量和深度作为计算数据来估算SOH。刘皓等[3]将遗传算法（Genetic Algorithm, GA）运用到SVR模型中，通过对模型进行优化实现SOH估计。DONG等[4]将粒子滤波（Particle Filtering, PF）应用到SVR模型中，实现SOH在线监控。孙培坤[5]选择GPR作为计算模型，将健康因子作为计算数据来估算SOH。王耀等[6]选择GPR作为计算模型，将容量作为计算数据来估算SOH，也有研究将等效电路模型和机器学习法相结合进行电池性能估计。潘海鸿等[7]通过将电池实际应用中的电流、电压数据输入到等效电路模型中，得到电池电阻，将内阻输入到极限学习法（Extreme Learning Machine, ELM）中对容量变化进行预估，进而计算SOH的变化。

1 健康因子

1.1 试验数据介绍

本文估算SOH的试验数据来源于NASA PCoE官网，电池的基本信息为电池型号：18650；标称电压：3.6 V；额定容量：2 Ah；放电截止电压：3.2 V；充电截止电压：4.2 V；工作温度：0～60 ℃。

试验将电池分为5组，每组由3到4个电池组成，在不同的温度、放电电流、放电截止电压情况下进行循环的充电、放电试验。选取B05、B06、B07号电池的试验数据进行研究，试验信息为环境温度：24 ℃；充电电流：1.5 A；放电电流：2 A；放电截止电压分别为2.7 V(B05)、2.5 V(B06)、2.2 V(B07)、2.5 V(B08)。

1.2 健康因子分析和提取

电池健康因子（Health Index, HI）可以用来体现电池SOH，直接HI由容量和电阻等组成，通过定义公式直接计算SOH。但由于这些因子基本都是需要在电池不工作时对电池相关参数进行测试，获得数据，不便于在车主用车过程中进行SOH估计。因此，希望选取电池使用过程的参数，即间接HI来进行电池SOH估计，综上所述，间接HI的选取也成为研究热点。间接HI一般从电流、电压和温度变化曲线中提取，并和机器学习算法结合来估计SOH。高栋等[8]在充电电流数据中提取电流下降的平均值作为间接HI，对电池容量进行估计。

本文选取容量作为直接HI，并基于试验数据对不同充电周期下的电压变化曲线进行分析，选取恒压充电时长、等电压上升充电时间、相同时间内电压上升值共计3个间接HI。首先计算间接HI，再定量分析出各间接HI与容量的相关性，确定相关性最强的间接HI，用于估计SOH。间接HI的计算方法如下：

1）恒压充电时长（Time of Constant Voltage Charge, TCVC）是电池充电时先恒流充电，再恒压充电，从电池开始恒压充电时开始计时，直到电池充电结束时终止计时，即

式中，2为充电完成的时间；1为开始恒压充电的时间；为电池充放电的循环周期。

2）等电压上升充电时间（Charge Time Equal Voltage, CTEV）是电池充电时相同电压变化区间所用的充电时长，研究选用电池充电时电压从 3.9 V上升到4.2 V所用的时间，即

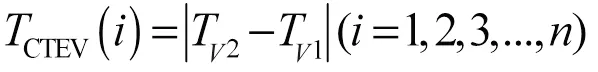
式中，T2为4.2 V电压时对应的充电时间；T1为3.9 V电压对应的充电时间；为电池充放电的循环周期。

3）相同时间内电压上升值（Voltage Rise of Equal Time, VRET）是从电池充电开始计时，500 s后计时结束，这段时间内的电压变化值为

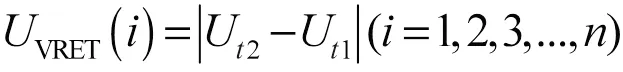
式中，V2为500 s后电池的电压值；V1为刚开始充电时电池的电压值；为电池充放电的循环周期。

利用Pearson和Spearman相关系数计算间接HI 与容量之间的相关性，结果如表1所示。

表1 间接HI与容量的相关性

项目TCVCCTEVVRET Pearson相关性-0.976 60.991 1-0.979 8 Spearman相关性0.991 60.994 10.990 7

由表1数据可知，CTEV与容量的相关性系数都在0.99以上，比另外两个间接HI与容量的相关性更高，因此，选择CTEV作为估计电池SOH的间接HI。

2 健康状态估计

2.1 高斯过程回归

当样本数据较少时，可用GPR建立预测模型，并输出预测值[9]，本研究中的电池样本值较少，因此，选用GPR构建预估模型对SOH进行估值。

在构建GPR模型时，核函数的选取对模型的估计精度影响较大。GPR模型的核函数种类多样，不同的核函数，适用的数据处理情景也不同，本研究的试验数据中SOH衰减较慢，且间距较小，因此，选用均方指数协方差函数（Squared Expone- ntial covariance function, SE），其表达式为

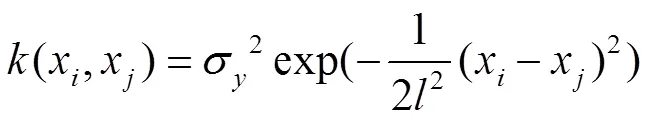
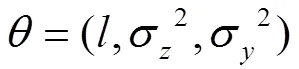
由贝叶斯定理得，的边际似然函数的表达式为

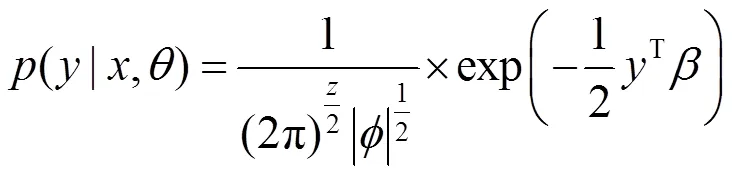
采用共轭梯度法（Conjugate Gradient Method, CGM）求解最优解时，速度快且计算量少，因此，本文选择CGM求取式（6）的最优解，构建GPR模型。

2.2 SOH估计模型及结果分析

SOH估计模型使用电池SOH，其计算公式为

式中，n为当前电池最大容量；rate为额定容量。

选取B05电池的CTEV和SOH作为模型的输入和输出对模型进行训练，利用训练好的模型对B05、B06和B07的SOH进行预测。GPR-SOH估计模型的步骤如下：

1）从B05、B06、B07电池的不同循环周期充电电压曲线中提取CTEV，计算出对应周期的SOH作为总样本；2）选取B05电池的试验数据对CGM-GPR模型进行训练，利用B06和B07电池的试验数据验证模型的预估效果；3）利用CGM对GPR模型进行超参数求解，建立GPR-SOH估计模型，对模型的估计进行量化分析。

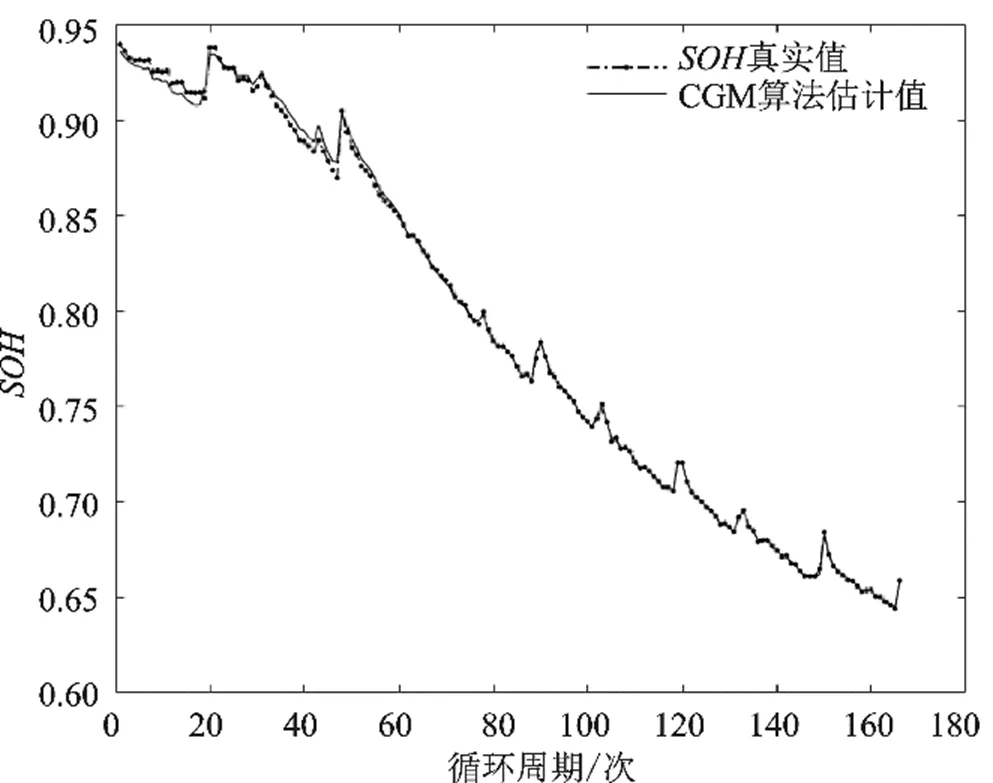
图1 B05电池的SOH真实值和估计值

B05电池的真实值和基于CGM-GPR模型的估计值如图1所示。

在电池充放电循环初期，B05电池SOH的估计值和真实值曲线有部分差异，随着循环周期的增加，SOH的估计值曲线和真实值曲线基本重合，说明CGM-GPR模型能够很好地对B05电池SOH进行估计。

运用最大估计误差（Max Error, ME）和均方根误差（Root Mean Square Error, RMSE）计算模型的拟合精度和预测效果，结果如表2所示。

表2 电池SOH估计误差分析

电池编号MERMSE B050.008 50.002 6 B060.029 80.019 3 B070.016 90.007 9

由表2数据可知，由B05电池试验数据训练的模型，对B05电池的SOH进行估计，最大估计误差为0.008 5，预测效果显著。利用该训练模型对B06和B07电池的SOH进行估计，B06电池SOH最大估计误差为0.029 8，B07电池SOH最大估计误差为0.016 9，说明基于等电压上升充电时间这一间接健康HI构建的CGM-GPR模型对同型号电池SOH的估计效果较好。

3 结论

本文选取锂离子电池试验数据为研究对象，将电池容量作为直接HI，基于电池充电过程中的电压变化曲线提取了3个间接HI，计算其与容量的相关性，得到相关性最强的间接HI。将间接HI作为模型输入，电池SOH作为模型输出，基于GPR建立SOH估计模型，运用CGM算法计算超参数，对电池SOH进行估计，分析拟合和估计效果，结果表明，基于CTEV这一间接HI构建的CGM-GPR模型能够很好地对同类型电池的健康状态进行估计。

[1] YOU G W,PARK S,DUKJIN O.Real-time State-of- health Estimation for Electric Vehicle Batteries:A Data-driven Approach[J].Applied Energy,2016,176: 92-103.

[2] 李刚,谢永成,李光升,等.基于自适应神经网络模糊推理系统的蓄电池SOH预测[J].微型机与应用, 2011, 30(22):82-84,87.

[3] 刘皓,胡明昕,朱一亨,等.基于遗传算法和支持向量回归的锂电池健康状态预测[J].南京理工大学学报,2018,42(3):75-80,97.

[4] DONG H,JIN X,LOU Y,et al.Lithium-ion Battery State of Health Monitoring and Remaining Useful Life Prediction Based on Support Vector Regression-particle Filter[J].Journal of Power Sources, 2014,271:114-123.

[5] 孙培坤.电动汽车动力电池健康状态估计方法研究[D].北京:北京理工大学,2016.

[6] 王耀,王哲,谢先宇,等.基于数据驱动的动力电池组健康状态评估[J].机电一体化,2019,25(3):3-9.

[7] 潘海鸿,吕治强,付兵,等.采用极限学习机实现锂离子电池健康状态在线估算[J].汽车工程,2017,39(12): 1375-1381,1396.

[8] 高栋,黄妙华,周亚鹏.基于充电电流数据的锂电池容量估计[J].电源技术,2018,42(10):1447-1450,1581.

[9] 康军,段宗涛,唐蕾,等.高斯过程回归短时交通流预测方法[J].交通运输系统工程与信息,2015,15(4):51- 56.

State of Health Estimation of Lithium-ion Batteries for Vehicles

HU Huimin1,2, PANG Zhifei1

( 1.Key Laboratory of Operation Safety Technology on Transport Vehicles, Ministry of Transport of the People'sRepublic of China, Beijing 100736, China; 2.School of Automobile, Chang'an University, Xi'an 710064, China )

Lithium-ion batteries are the main source of power for new energy vehicles, and their status of health estimation is closely related to battery maintenance, repair, and replacement. In this paper,battery capacity is selected as a direct health factor, three indirect health factors are extracted based on battery charging voltage curve, and the correlation between them and capacity is calculated using Pearson and Spearman correlation coefficients.The results show that the correlation between charge time equal voltage and capacity is the highest. Gaussian process regression (GPR) algorithm is selected to establish the state of health(SOH) estimation model, and conjugate gradient method (CGM) is selected to calculate the hyper parameter of the model, which can better estimate the SOH of lithium-ion batteries.

Lithium-ion batteries for vehicles;SOH; Health index; Gaussian process regression

10.16638/j.cnki.1671-7988.2023.020.001

U469.72

A

1671-7988(2023)20-01-04

胡慧敏（1994－），女，助理工程师，研究方向为BMS软件，E-mail:hhuimin1113@163.com。

运输车辆运行安全技术交通运输行业重点实验室开放课题（KFKT2018-01）。