Planar peristrophic multiplexing metasurfaces

Jia Chen, Dapeng Wang, Guangyuan Si, Siew Lang Teo,Qian Wang and Jiao Lin

Keywords: peristrophic multiplexing; metasurface; holography

Introduction

In modern communications and optical data storage applications, multiplexing plays an essential role by combining multiple signals together to enable the transmission of non-interfering, different signals in the same channel, significantly increasing the capacity and spectral efficiency of the system. In recent decades, many types of classic multiplexing techniques, i.e., frequencydivision1-3, time-division4,5and code division multiplexing6,7, have been developed to achieve reliable storage and communication of information. On the other hand,with the advent of advanced nanofabrication techniques,metasurface-based holograms have gradually become a promising approach due to the flexibility and miniaturization. Metasurface is a kind of two-dimensional artificial materials with unique electromagnetic properties8-16,which has the capacity to arbitrarily control the wavefront of light. Remarkably, the revolutionary meta-atoms are rationally engineered to outperform traditional display, holographic, and multiplexing technologies in the aspects of good compatibility, chip-scale footprint and high integration.

Note that the degree of freedom (DoF) is the cornerstone of multiplexing methods. Nowadays, a great number of impressive efforts have been devoted to dividing various physical properties as the discriminating DoFs,including wavelength17, polarization18, and spatial modes19. Moreover, a nontrivial phase mode, named orbital angular momentum (OAM), has been recently exploited for planar multiplexing20-23. However, the prerequisite for OAM multiplexing is the pixelation of target information, resulting in discretized recording and playback. Besides the above-mentioned DoF individually, recent progresses extensively focusing on multifreedom multiplexing have been made, such as wavelength-polarization synergism24,25, polarization-location synergism26, polarization-angle synergism27, spatial and angle synergism28, surface and free-space mode synergism29, and wavelength-polarization-OAM synergism30.Although these strategies enhance the data encoding and channel addressing capacity, the joint mechanism requires a very intricate system and meanwhile brings about the interdependency among the DoFs. Thus, contemporary technologies are still facing a critical challenge in exhausted DoF.

By revisiting traditional volume holography, there is a peristrophic (Greek for rotation) multiplexing in which the encoding information can be retrieved through the rotation of the sample axis31,32. This classic method provides abundantly independent recording and retrieving channels. It nonetheless has limitations including bulky size, sluggish response time, and the presence of specific crosstalk33,34, which dramatically reduces multiplexing efficiency. More importantly, the fundamental principle of traditional peristrophic multiplexing is ascribed to the Bragg condition that only occurs on a very thick holographic material35. As an alternative, Wei et al. presented a rotational multiplexing method based on cascaded metasurfaces36. Yet it inevitably leads to the intractable issues of fabrication and alignment processes.Thus, the demand of additional DoF motivates us to seek a more convenient method of implementing multiplexed holography and further refining the dimensionality of thin holographic methods.

In this work, we propose a planar peristrophic multiplexing metasurface that combines the concept of spatial frequency orthogonality with an innovative detour phase principle. We explore an unprecedented sub-wavelength detour phase configuration, which effectively eliminates the twin-image issue. The undesirable diffraction orders can be suppressed via the spatial frequency selection rule,resulting in the enhancement of diffraction efficiency.We experimentally investigate a proof-of-concept metasurface to verify the viability and flexibility of peristrophic multiplexing. Given that the proposed metasurface has the distinctive merits of wavelength and polarization independence, our finding can be regarded as an additional DoF for multiplexed holograms. In the meanwhile, the method is also compatible with conventional DoFs.

Methods design and principle analysis

The conceptual scheme of planar peristrophic (or rotation) multiplexing metasurface is shown in Fig. 1(a). A polarization-independent probe beam impinges on a thin holographic metasurface of which the period of unit cells and structural sizes are subwavelength. When the hologram is physically rotated, the rotation axis is generally perpendicular to the surface of the metasurface. In this case, the multiplexed holograms can be accordingly achieved. Compared with traditional volume holography in which peristrophic mechanism is fundamentally obtained via the Bragg selection of layer-by-layer interference31,37-40, the breakthrough of our proposed thin metasurface is made by a combination of sub-wavelength detour phase principle and the spatial frequency of incident light. During the rotation process, thek-vector of the probe beam satisfies a special spatial frequency range and then the holographic playback carrying information can be diffracted into the targeted diffraction order. Due to the subwavelength property, the twin image diffraction order will be suppressed, which greatly alleviates the energy loss. Furthermore, the multiplexing realization of peristrophic holograms is attainable through the spatial locations of building blocks. The newly explored attribute can be therefore adopted for an additional DoF regardless of wavelength and polarization, dramatically enhancing the number and capability of multiplexing channels.

Fig. 1 | (a) The principle of the planar peristrophic (or rotation) multiplexed hologram. The holographic metasurface consists of a series of dislocated nanostructures and according to the relative position of adjacent building blocks, arbitrary phase modulation is attainable. When a monochromatic polarization-independent plane wave impinges on the peristrophic metasurface, the multiplexed holograms can be achieved through the spatial orthogonal directions for retrieving the images of “H” and “V” and the twin image diffraction order is blocked. (b) The schematic diagram of the multiplexing condition during the peristrophic process. At a specific rotation angle, there is an optimized spatial frequency range that satisfies the multiplexing condition.

To primarily engineer the metasurface in a universal way, isotropic building blocks, i.e, nanohole structure,are chosen for independent holograms. Though the similar nanoholes were widely used in nanosieve holograms with the capacities of high efficiency, ultra-broadband and large angle-of-view41-43, we capitalize on the counterparts and put forward a novel subwavelength detour phase principle which excels at high fidelity holography due to the pure phase modulation. The phase distributions of multiplexed information are recorded individually according to the spatial orthogonality of the detour phase principle. The metasurface achieves arbitrary 0-2π phase modulation by dislocating the distances between adjacent nanoholes, which has the desirable characteristics of versatility and flexibility. The conceptual schematic with respect to the peristrophic metasurface is shown in Fig. 1(a) and the principle of the detour phase is represented in Fig. S1. The relative displacement of nanohole structures in different directions is realized successively by the traditional detour phase method44,45. Note that the retrieving mechanism of the peristrophic metasurface and the sensitivity of the meta-hologram to the spatial frequency of incident light allow us to achieve multiplexed holograms. There is a spatial frequency boundary of the incident light, which means that a certain spatial frequency input can excite a hologram whilst the other hologram in the orthogonal direction is inhibited. As a result, the spatial frequency range plays a key role in the multiplexing of the meta-hologram, which has the powerful ability to simultaneously achieve both the multiplexing capacity and the suppression of twin image order without enlarging the device footprint.

Figure 1(b) shows the multiplexing rule of the spatial frequency orthogonality of peristrophic metasurface.When the hologram is rotated to a given angle, the spatial frequency region (e.g.,kx,ky) of the probe beam should belong to the external crucial frequency region where multiplexed holograms can be performed. Hence,there is a boundary limitation for the selection of incident light. Furthermore, it is found that two orthogonal points can be regarded as the key points for judging the multiplexing condition. Assuming that the spatial frequency of an obliquely incident light remains constant,e.g., a fixed coordinate points in blue, yellow, or green area, the multiplexing is attainable by means of the oblique irradiation onto a peristrophic metasurface, and the rotation can be used to selectively reconstruct different target images.

In the following, we focus on the mathematical discussion specific to the multiplexing principle of spatial frequency orthogonality condition. The visual analysis results are shown in Fig. 2. As shown in Fig. 2(a), the distinguishing playback of holograms is attainable through the relative rotation around the rotation axis 1 and 2 normal to the multiplexed metasurface. As shown in Fig. 2(b),considering a monochromatic incident light with a special spatial frequency and the wave vector ofkwave(kwave∈[kx,ky]), the direction cosine matrix is expressed askwave_x=(2π/λ)cosαandkwave_y=(2π/λ)cosβ, whereαandβare the azimuth angle. Thek-vector of the input probe beam meets the following condition for multiplexing inkxdirection

Fig. 2 | The multiplexing rule of spatial frequency orthogonality. When an addressed incident monochromatic chromatic plane wave with vector kwave satisfies the different threshold hologram conditions, the metasurface is viable to realize the multiplexing through the rotation along the z-axis, which means that a target hologram is encoded with one special spatial frequency of input beam and the other one is encoded with the orthogonal spatial frequency. (a) Schematic diagram of a peristrophic multiplexed metasurface combined the spatial frequency orthogonality with the subwavelength detour phase principle. (b) Spatial frequency multiplexing condition for the hologram in the kx direction (blue area). (c)Spatial frequency multiplexing condition for the hologram in the ky direction (green area). (d) Orthogonal spatial frequency multiplexing relationship.

whereks=2π/ais the spatial frequency of the periodic structure,ais the unshifted period of unit cells. The excited hologram, in this case, is only inkxdirection, while the other orthogonal direction cannot generate a hologram because of the diffraction suppression. And the wave vectorkwavefalls within the blue region in Fig. 2(b).Similarly, when the metasurface is rotated to 90° along thez-axis, the direction cosine of the wave vectorkwaveas shown in Fig. 2(c) meets the following condition for multiplexing inkydirection

Only theky-direction hologram can be generated. And the wave vectorkwavefalls within the green region in Fig.2(c). It should be noted that when the wave vectorkwavefalls in the white region, no hologram can be generated in eitherkxorkydirection. Therefore, the orthogonality of the wave vectorkwavein two directions can be used to achieve a multiplexing strategy. The arbitrary wave vectorski1···kimin the blue region and the arbitrary wave vectorskj1···kjnin the green region as shown in Fig. 2(d)are selected to form a pair of wave vectors for multiplexing. For example, a pair of wave vectors,kimandkjn, is specifically selected to implement the dislocation of the building blocks, and eventually, the peristrophic metasurface morphology can be confirmed according to the detour phase method. Considering the elimination of multiplexing crosstalk during the reconstruction process,we choose a pair of wave vectors such aski1andkj1that are orthogonal to each other in the practical design.

Results and discussion

In order to verify the feasibility of our designed metahologram, the experimental setup is schematically shown in Fig. 3(a). A semiconductor laser with a wavelength of 532 nm is utilized as the laser source. A linear polarizer and aλ/2 plate were combined to produce linearly polarized light with a tunable polarization direction. Subsequently, the linearly polarized light is focused by a lens to concentrate the power and irradiate across the metasurface area. The meta-hologram is mounted on a rotation stage. Due to the high reflection of metal materials,we adopted an off-axis holography strategy. Then, the reflected diffraction order carrying the target information(n= +1) was received by a lens. The field of view (FOV)of the experimental system is around 22°. The retrieving image therefore suffers from an obvious divergence and even approach to the aperture limitation of the collecting lens before the CCD camera. Finally, its intensity distribution was captured by the CCD camera and appeared a little bit of holographic image distortion.

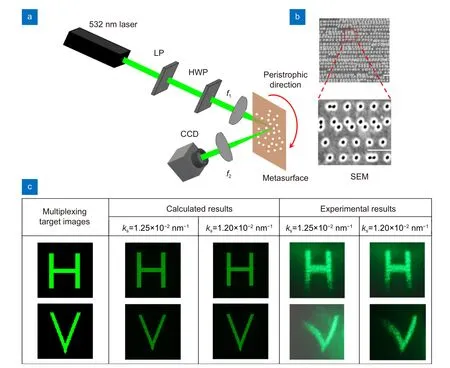
Fig. 3 | Experimental setup and results of peristrophic multiplexed holograms. (a) The far-field holographic system including a laser, a linear polarizer, a half-wave plate, two lenses (f1 =50 mm and f2 =50 mm) and a sample on a rotation stage. The holograms are captured by a CCD camera. (b) Top-view scanning electron micrograph photos of the fabricated metasurface (scale bar: 1 μm). (c) Calculated (based on Fourier transform) and the experimental results of the encoded “H” and “V” images. The holographic intensities are detected when the metasurface is rotated along the z-axis in different design ks.

Figure 3(b) shows a scanning electron microscope(SEM) image of the fabricated multiplexing metasurface(more details can be found in Supplementary information Section 3). Additionally, the effect of the thickness of the gold film and the diameter of nanoholes on the reflectance and transmittance of the wide spectrum is illustrated in Fig. S2 and Fig. S3 respectively, which is conducive to the design of the structural parameters. As shown in Fig. 3(c), we have numerically designed the multiplexed meta-hologram. Taking the 200★200 pixels images of “H” and “V” as an example, the required phase profile for a holographic image has been calculated based on Gerchberg-Saxton algorithm46,47. The convergence results and analysis of Relative Mean Square Error(RMSE) with different phase discrete orders are shown in Fig. S4. After mutually considering the multiplexing crosstalk and the fabrication difficulty, the phase profile is discretized into the three-level computer-generated holograms. The numerical results for the reconstruction atks=1.25×10-2nm-1andks=1.2×10-2nm-1obviously validate the multiplexing function. In addition, the finite-difference time-domain (FDTD) simulation results of transmission and reflection of metasurface at differentkwaveand oblique incident angles are shown in Fig.S5. The multiplexing playback holograms of “H” and “V”optionally appear when the designed meta-hologram is rotated along thez-axis. The image of the intensity distribution generated by the metasurface is shown in Fig.3(c). Similar to the numerical calculation, the multiplexed holographic images of “H” and “V” have been experimentally produced when the metasurface is illuminated by a laser beam. The calculated and experimental results are in accordance with the theoretically predicted profile. We also exhibit the experimental and simulation results of another multiplexing counterpart for double validating the viability of our design schemes (Fig. S6). In addition, the results of multiple-channel (such as four channels) multiplexing using a synthetic peristrophic meta-hologram are demonstrated in Fig. S7.

As an additional degree of freedom, the peristrophic multiplexing method is independent on the wavelength and polarization, which is different from the spatial and angle multiplexing reported in the reference28. Due to the isotropic nanohole and subwavelength essences, the proposed method is competitive in terms of polarization insensitivity, wide bandwidth and high tolerance of incident angle. To evaluate the performance of the polarization-independent feature, the reflection efficiency of the targeted diffraction order is separately measured by changing the polarization direction during the rotation process. The schematic diagram of diffraction efficiency(DE) measurement is shown in the following Fig. S8 and the experimental results are shown in the following Fig.4(a). The DE is evaluated by the ratio of the intensity of captured holographic image (+1st diffraction order) to the total reflected power (+1st diffraction order and zeroth diffraction order). It can be confirmed that the power evolution almost keeps unchanged regardless of the input polarized angles and the power error rate is less than 3%. The results of retrieving images at different polarized angles are shown in Fig. 4(b). It is demonstrated that the peristrophic multiplexing strategy is unaffected by altering the polarization directions and more importantly, the flexible DoF is compatible with the existing methods. Nevertheless, the absolute diffraction efficiency is relatively low in this stage. The obstacle of low DE is ascribed to the building blocks design. In the experiment, the holographic information on the +1st diffraction order was detectable whilst the majority of the reflected energy is still concentrated at the zeroth diffraction order (～70%). To further improve the efficiency, a few schemes with respect to engineer the building block architecture will be available. For instance, the utilization of nanodisks replacing nanoholes would be advantageous to the reflection-type holograms48or the metalinsulator-metal method can also reach an ultrahigh efficiency49. In regard to the transmitted configuration, our previous work has demonstrated over 90% conversion efficiency by means of dielectric building blocks50.

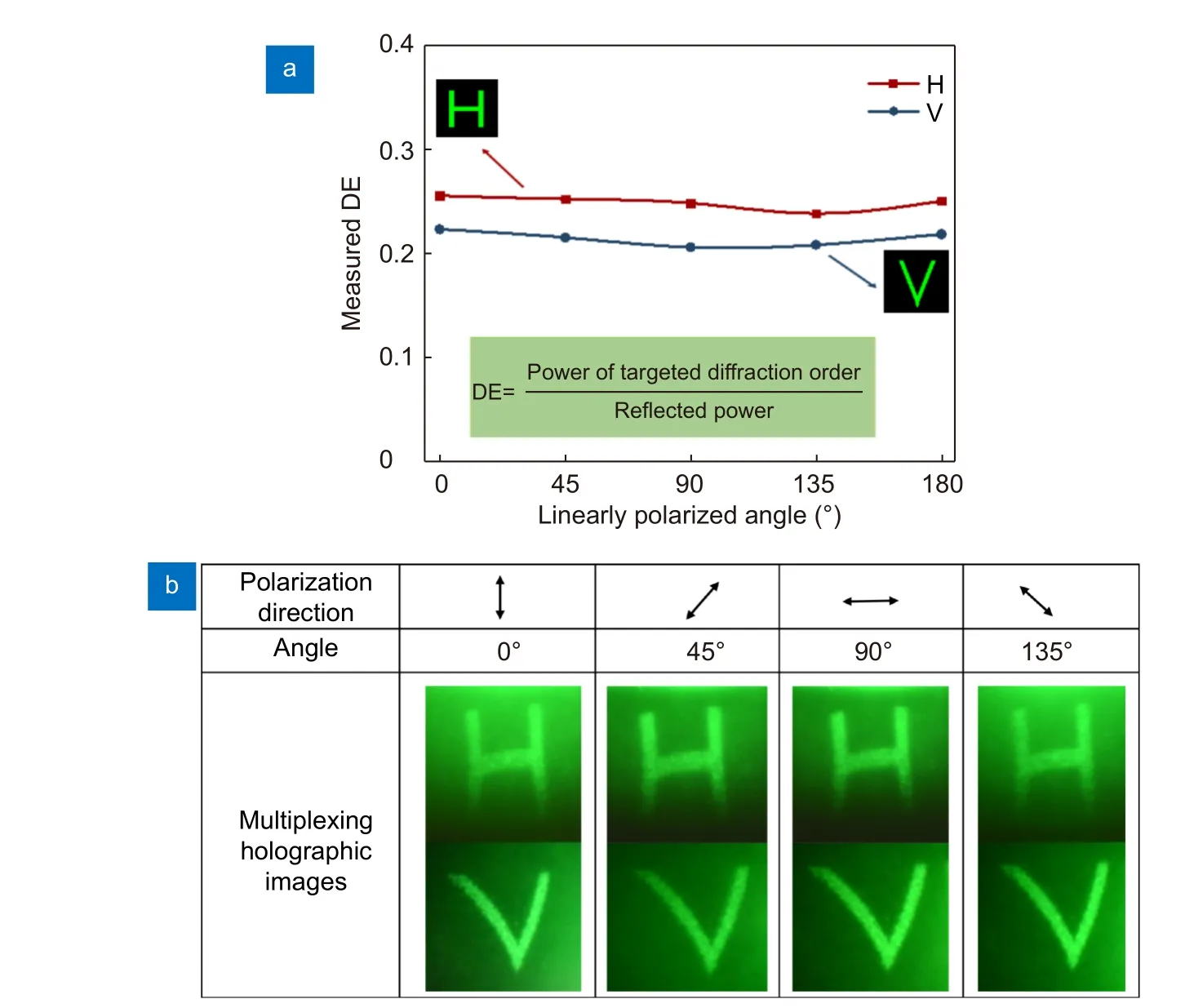
Fig. 4 | (a) The efficiency of the targeted diffraction order as a function of different linearly polarized angles (0°, 45°, 90°, 135°, 180°). Since the power of the reconstructed images maintains consistently under different linearly polarized angles, the multiplexing method does not depend on the input polarization. (b) The experimental results of holographic images at various polarization directions.

In addition to the broadband property of peristrophic metasurface, we experimentally measure the response to different wavelengths. Without the consideration of the effect of substrate material, film thickness and structural morphology of building blocks, the comprehensive analyses of holographic diffraction in theory can be interpreted from Fig. 5(a). In the case of the period ofa=500 nm, the wavelength as a function of incident angle is visually shown. It can be seen that there are several distinguishing regions bringing about different diffracted fields. For the region I (λ＜a), it is similar to the conventional detour phase diffraction. Though the multiplexing behavior is still likely to take place, the undesirable twin image order is also indispensably generated. As a consequence, the multiplexing efficiency will accordingly reduce. The regions II and II★(λ≥a) possess an exotic functionality, i.e, the suppression of twin image diffraction order. The sub-wavelength detour phase design can effectively optimize the distribution of diffraction order51. It is the relation of spectral and spatial frequencies that lead to the peristrophic multiplexing. There is a boundary of positive and negative diffracted angles, which means that they are separated from the normal line of sample. As for the region III (kwave＞ks),the reconstruction of hologram will disappear due to the deep subwavelength scale.

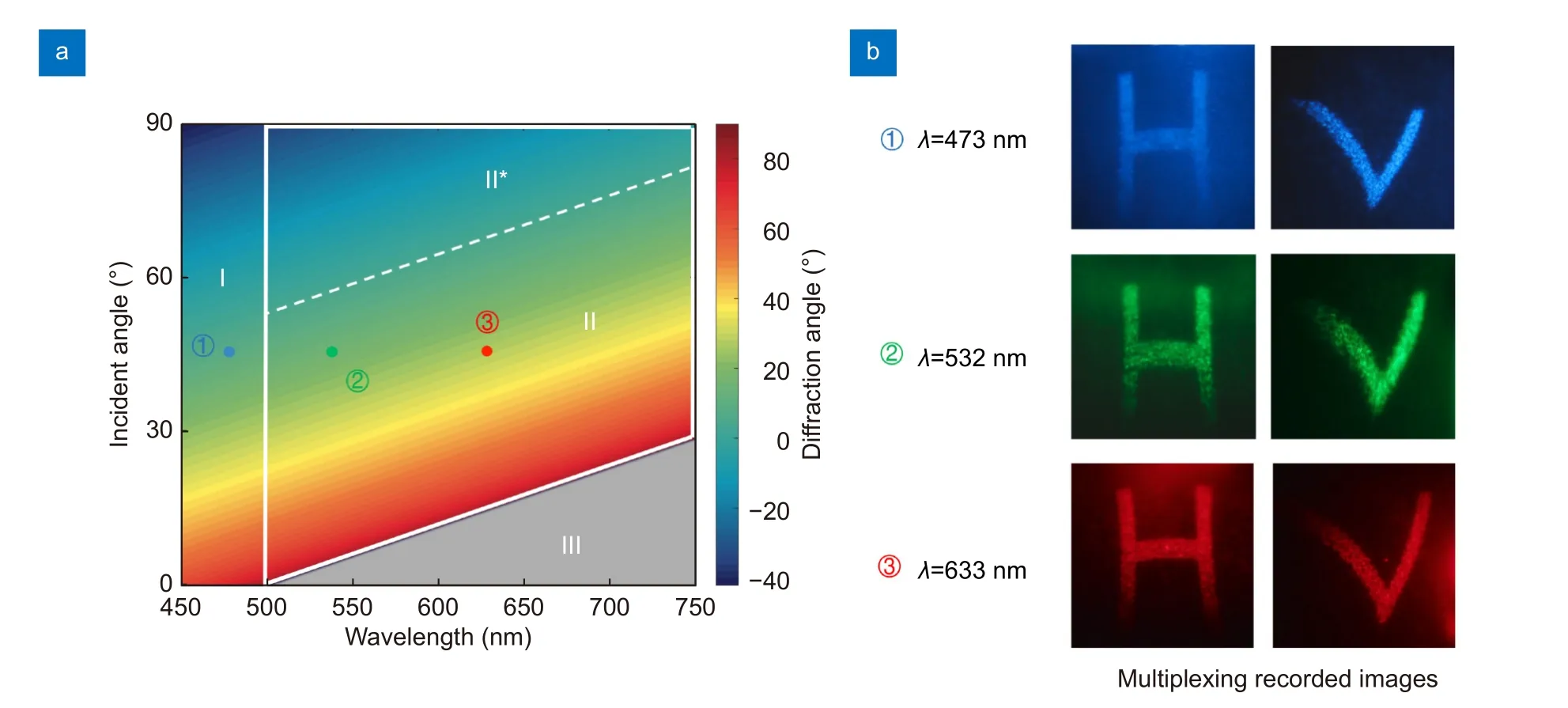
Fig. 5 | (a) The theoretical analyses of diffracted fields as a function of the spatial frequency and spectrum. (b) The experimental results of multiplexing images at different wavelengths of light (λ=473 nm, 532 nm and 633 nm).

It is worth mentioning that the white dotted line in Fig. 5(a) is the dividing line corresponding to the 0° diffraction angle. This is an optimized diffracted direction whereby the coaxial detection is attainable to the peristrophic strategy. Likewise, the boundary line between regions II and III is of importance to determine the minimum incident angle and a limit to the choice of incident light for the practical application. These findings enable to guide the device design and system integration in advance. Additionally, Fig. 5(b) shows the experimental results of rotational multiplexing at three wavelengths,which further verifies that our design holds great promise for broadband applications.

Conclusions

In summary, we have proposed and demonstrated a new type of holography multiplexing functionality based on peristrophic metasurfaces. By incorporating the concept of spatial frequency orthogonality with an innovative detour phase principle, the multichannel hologram through the peristrophic strategy is viable to selectively retrieve the encoding images on request. Without enlarging the device footprint, our method successfully increases the multiplexing capacity for storing information. More importantly, the method can be regarded as an additional DoF since it is independent on the wavelength and polarization. Compared with traditional detour phase and volume holography, the unprecedented sub-wavelength merit is conducive to eliminate the twin-image issue and significantly reduce the volumetric thickness. The proposed metasurface device taking the advantages of miniaturization, versatility, and broadband operation can be compatible with other DoFs multiplexing and therefore holds promise for large-capacity chip-scale applications.

Acknowledgements

This work is supported by the Science and Technology Projects of Innovation Laboratory for Sciences and Technologies of Energy Materials of Fujian Province (IKKEM) No. HRTP202231 and partially supported by the Agency for Science, Technology, and Research (A★STAR) under AME IRG Grant Nos. A20E5c0095, and CDF Grant No. C210112044. This work was performed in part at the Melbourne Centre for Nanofabrication (MCN) in the Victorian Node of the Australian National Fabrication Facility (ANFF).

Author contributions

D. P. Wang and J. Lin conceived the idea and supervised the research. J.Chen and D. P. Wang performed theoretical descriptions and device designs. G. Y. Si and S. L. Teo prepared the samples and implemented the nanofabrication. J. Chen, D. P. Wang and Q. Wang completed the optical measurements and analyzed the results and data. All authors discussed and wrote the manuscript.

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary information for this paper is available at https://doi.org/10.29026/oea.2023.220141