基于标签相关性的预测调整算法

张海涛，王丹东，钱 坤，闵 帆

（西南石油大学 计算机科学学院，成都 610500）

0 引言

多标签学习（Multi-label learning[1］，MLL）由于应用的广泛性而在机器学习中获得学者的高度关注。在文本分类中[2-3］，MLL 能够对文本数据中的多个主题进行分类建模，例如论文、作者和出版场所等，并提供有价值的服务，例如推荐和信息检索等。在图像分类中[4-5］，多标签学习与传统的多类分类相比，它具有利用多个标签来捕获图像中丰富信息的优势，并利用潜在信息标签之间的联系对捕获信息进行优化，以提高预测准确性。在视频注释中[6］，多标签学习通过利用标签相关性来推断与其他概念相关的复杂概念，从而提高视频浏览、搜索和导航的可靠性。

已经有许多技术被用来解决多标签分类的问题。为了解决标签稀疏问题[7-8］，X-Transformer 模型[3］用于确保正负标签的平衡。为了解决缺失标签问题，DM2L（Discriminant multi-label learning with missing labels ）算法[9］通过在预测中加入高秩结构来解决问题，以获得更好的可区分性。LEML（Large-scale multilabel learning with missing labels）算法[10］在一般的经验风险最小化（Empirical Risk Minization，ERM）框架下研究了多标签问题。GLMA（Global and local attention-based multi-label learning with missing labels ）算法[11］使用注意力机制来共同利用标签和实例信息，以提高恢复标签的质量。对于噪声标签，CS2PML（Semi-supervised partial multi-label classification via consistency learning ）[12］采用一致性学习技术处理部分标签，无须恢复地面实况标签。关于利用标签相关性[13-16］，ACkEL（Active k-labelsets ensemble for multi-label classification ）算法[17］将多标签问题转换为一组多分类问题。BP-MLL（Multilabel neural networks with applications to functional genomics and text categorization ）算法[18］和MASP（Multilabel active learning through serial-parallel neural networks ）算法[19］使用神经网络来捕获标签相关性。

在目前的多标签学习领域，大多数方法倾向于采用线性模型，然而，这种简单的线性模型并不能充分挖掘特征中潜在的标签相关性，从而限制了多标签分类任务的性能。多标签分类的复杂性在于一个样本可能与多个标签相关联，而这些标签之间可能存在非线性的关系。同时，现有的多标签学习算法在考虑标签相关性时主要采用经验模型，这种方法是基于以往经验的启发式规则或简单的标签关联度来进行建模。这种经验模型往往会忽略潜在的、未知的标签之间的相关性。在实际应用中，许多标签之间可能存在更加复杂的联系，而这些联系仅通过经验模型无法获取。

为了标签的共现分配更高权重，以获得更好的预测结果，本文重点研究通过标签相关性来调整预测结果的新算法PALC（Prediction adjusting with label correlation）①本文算法源代码已公开，可在GitHub上获取，网址为github.com/1808459537/PALC。，以及研究如何将标签相关性融入串并联神经网络中。

1 相关工作

本章首先介绍PALC 所使用的数据模型。随后，简要回顾了解决多标签学习问题的各种技术，包括串并联神经网络和标签相关性的利用。

1.1 数据模型

为了简便起见，通过表1列出了本文中使用的一些重要符号表示。由表1可见，数据矩阵用X来表示，该矩阵有n行m列，其中n表示样本数量，m表示特征数量。每条样本数据：xi对应于一个特定的实体，比如一首音乐或一张图片。标签矩阵用Y=[yik]n×l表示，其中l表示标签数量。当yik= 1时，表示xi具有第k号标签，而yik= 0时，则表示xi不具备该标签。

表1 符号含义表

1.2 多标签学习中的标签相关性方法

在多标签学习中，标签相关性扮演着关键的角色，主要包括两类方法。第一类方法专注于独立地分析标签矩阵。例如，GLOCAL（Multi-label learning with global and local label correlation）算法[20］1081将标签矩阵分解成低秩子空间，并构建线性预测模型。Haripriya 等[21］利用k-means 算法将关联规则挖掘算法（Apriori）[22］的预处理空间划分为簇，并为每个簇生成关联规则。LSFCI（Multi-label learning with label specific features using correlation information）算法[23］利用概率邻近图模型和余弦相似性来捕捉实例和标签空间的相关性。LFCMLL（Joint label-specific features and correlation information for multi-label learning ）算法[24］通过线性回归为每个标签学习稀疏权重参数向量，直接约束输出中的标签相关性。此外，2SML（Weight matrix sharing for multi-label learning ）算法[25］利用特征流形和标签流形的相关信息来促进共享权重的学习。第二类方法主要考虑在每个学习子问题中处理标签的子集。LP（Learning multi-label scene classification）算法[26］通过逐个考虑一个标签子集来处理多标签问题，将其转化为一组多类别学习问题。EMLC（Ensemble methods for multi-label classification）算法[27］选择了最少的k个标签子集，以覆盖所有标签并满足其他约束。RakEL（Random k-labelsets for multilabel classification ）算法[28］将初始标签集分解为固定长度的随机子集。

1.3 多标签学习的神经网络模型

利用神经网络可以更有效地捕捉数据的内在特征。Kurata等[29］提出了一种新颖的神经网络初始化方法，将最终隐藏层中的某些神经元视为专用神经元。Huang 等[30］提出了一种多任务深度神经网络架构（MT-DNN）来处理多标签学习问题，其中每个标签学习被定义为一个二分类任务。ADD-GCN（Attentiondriven dynamic graph convolutional network for multi-label image recognition）算法[31］采用了动态图卷积网络来建立内容感知类别表示的关系，这些表示由语义注意模块生成。

2 主要算法

本章将给出主要算法，其中包括网络设计、标签相关性探索和简单的优化方案。下面将详细描述每个组件，并解释它们如何共同为我们的方法的整体效果做出贡献。

2.1 网络模型的设计

本研究采用了一种串并联的神经网络作为多标签分类器。此外，为了解决并行网络中缺乏全局信息的问题，算法在并行网络之前加入了原始数据信息，图1为串并网络示意图。

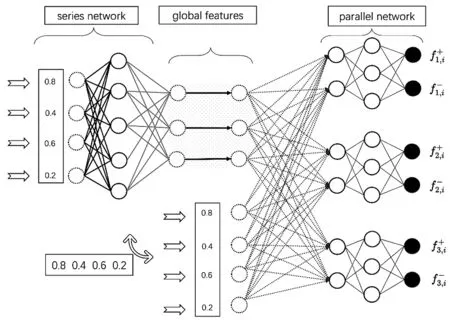
图1 串并网络示意图

为了处理网络的输出，训练标签矩阵Y被扩展为一个成对标签矩阵，表示为Y*。这个扩展是通过将1和0表示为[1，0］和[0，1］来完成的。举例来说，如果原始标签向量yi=[1，1，0］，那么扩展后的成对标签向量将是yi*=[1，0，1，0，0，1］。为了优化网络，实验使用均方误差（Mean-Square Error，MSE）来计算fΘ和Y*之间的误差。优化问题可以表示为

其中fΘ是神经网络对整个训练集的输出。

2.2 标签相关性和流形正则化

本节的目标是探索和识别标签相关性。为了使用标签相关性，我们根据Y的特性构建了一个标签相关性矩阵C=[] ，其中cij的定义为

在这里，λ1、λ2、λ3是权衡参数，且满足λ1＞λ2＞0＞λ3＞-λ1。当标签i和j一起出现时，它们对相关性的贡献相比于它们同时缺失时更大。相反，如果只有一个标签出现，其贡献被认为是负面的。

此外，C是一个实对称矩阵，cij被视为标签i与标签j的相关性。当标签i和标签j之间的相关性很强时，对应的相关系数cij会很大，否则会很小[32］。在这里，标签相关性矩阵C可以用来调整参数和正则化模型。假设第i个标签与第j个标签具有很强的相关性（即cij或cji很大），它们在同一时间会高概率出现。令fi，：表示分类器第i行输出向量，即因此，当cij很大的时候，我们认为预测结果fi，：和fj，：应该保持一致的相关性和相似性。简言之，相应的分类器输出是接近的，反之亦然。用以下公式

表示这一特性，希望将公式（6）的值最小化。在算法PALC中，标签相关性矩阵将以流形正则化的方式优化串并联神经网络。对于成对输出，流形正则化侧重于调整负类输出，这样不仅可以调整模型的相关性，还减少了过拟合的可能性。结合串并神经网络，得到以下优化问题：

其中α是权衡参数。

同时，每个标签的二值化可以被视为完全负相关。因此，希望每一对端口的最终结果尽可能地负相关。设，则优化问题表示为

其中：β是一个权衡参数；ζ=[ 1，1，…1 ]∈Rn。然后，用图拉普拉斯矩阵L来优化公式（8），其中L=D-C，D是从标签相关性矩阵C计算得到的对角矩阵。优化问题被简化为

2.3 优化

在第2.2节中，问题的优化被归因于公式（9），接下来将简要解释其优化过程。为了更清楚地说明该过程，公式（9）需要被重新表示为

下面采用Adam优化算法来更新神经网络模型的参数，旨在实现更快的收敛和改进泛化能力。为了计算梯度，可以使用如下公式

经过多次迭代后，网络模型可以用于对新样本进行预测。如果预测结果中则可以推断第j个实例的第i个标签存在；否则，该标签不存在。

3 结果与分析

3.1 数据集和评价指标

本节评估PALC 的性能。表2 列出了来自不同领域的一组数据集，包括音乐、医学、图像、生物学等。这些数据集都可以从可靠的来源（如Mulan2、KDIS3和PALM4）免费下载。在这些数据集中，有8个属于非文本领域，而其余2 个属于文本领域。通常情况下，多标签学习常常面临标签稀疏性，类似于单标签学习中的类别不平衡问题。因此，像Micro-AUC、PeakF1和NDCG这样的排名型评估指标适用于这个任务。

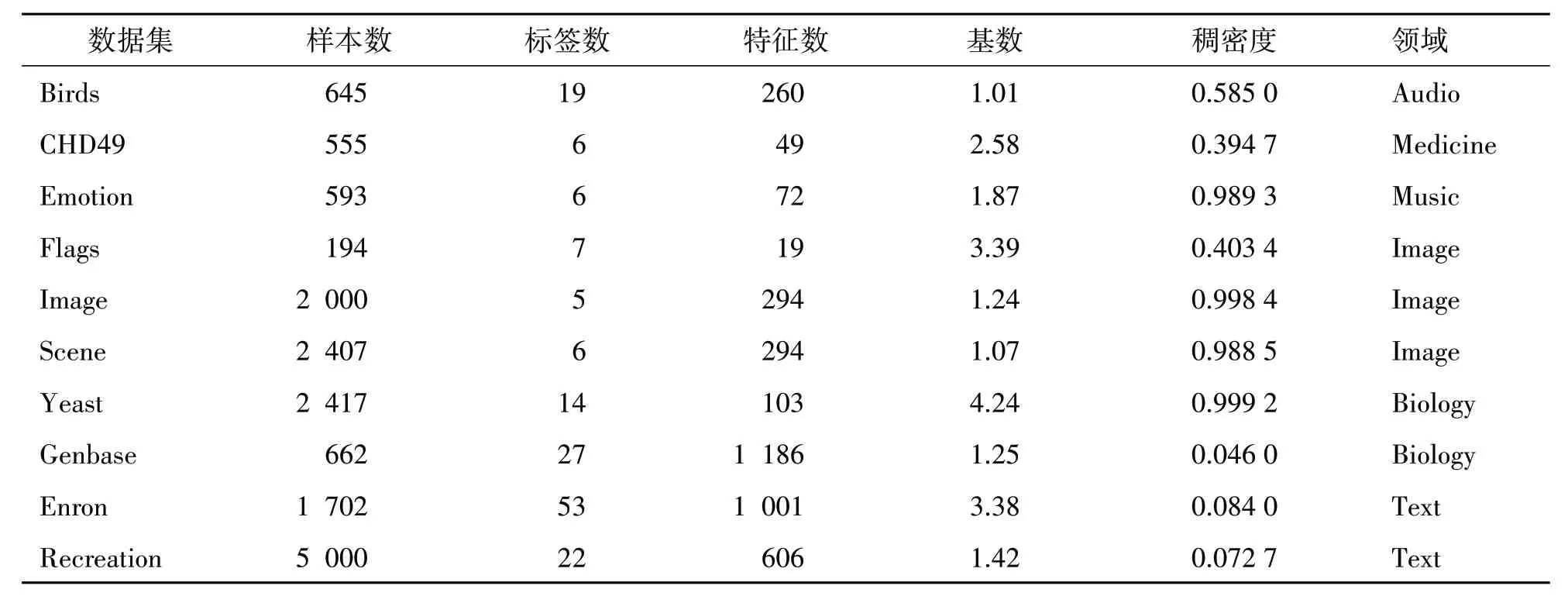
表2 实验数据集

Micro-AUC（曲线下面积，MAUC）是多标签学习中的代表性评估指标，通过计算ROC 曲线下的面积来得出。ROC 曲线是从混淆矩阵得到的真正率（TPR）值和假正率（FPR）值衍生而来。假设m和n分别是正标签和负标签的数量，表示正标签集合，则计算方式可表示为

其中：rl表示标签l在预测结果排序后所在的位置。

PeakF1分数是在多标签学习中广泛使用的无阈值评估指标。它是从F1分数衍生而来，F1分数评估了精确率和召回率之间的平衡。为了计算PeakF1分数，根据标签的预测概率进行排序，通过将前k个标签视为正例，其余的标签视为负例，计算F1分数，即

其中：P代表精确率；R代表召回率。

归一化折损累积增益（Normalized Discounted cumulative gain，记作NDCG）在衡量模型预测结果的排序质量方面发挥重要作用。用DCG（Discounted Cumulative Gain，缩写为DCG）表示一种强调整体排序对预测结果影响的度量，则NDCG是DCG的改进版本。它是基于标签按照预测概率从高到低进行排序后的序列，其中每个标签对应一个增益gi。DCG可以通过将每个增益gi与其所在的位置序数的对数（以2为底）之间建立关系，然后进行累加求和得到：

在公式（20）中，i表示标签在排序后的序列中的位置。IDCG（其数值记作DICG）可以被视为处于最佳排序状态的DCG。为了计算DICG，将标签按照原始标签矩阵Y进行排序。假设在Y矩阵中有k个正标签，那么排序后的数组包含所有位于区间[1，k］中的正标签和所有位于区间[k+1，nq］中的负标签。可以通过公式（20）和这个排序后的数组来计算DICG。最终通过将DCG除以DICG，就得到NDCG，它是DCG的归一化版本，用于将结果映射到0到1之间的范围。NDCG的计算公式为

3.2 实验效果比较

在比较评估中，本研究将算法与几个著名的算法进行了比较。这些基准算法涵盖各个类别，包括第一个多标签神经网络算法（BP-MLL[18］），多标签惰性学习方法（MLKNN[33］和IMLLA[34］），基于标签相关性算法（GLOCAL[20］1088和LSML[35］），噪声感知方法（PML-NI[36］）和多标签主动学习技术（MASP[19］）。表3～5展示了实验的对比结果，表中加下划线的数值表示最佳表现结果。

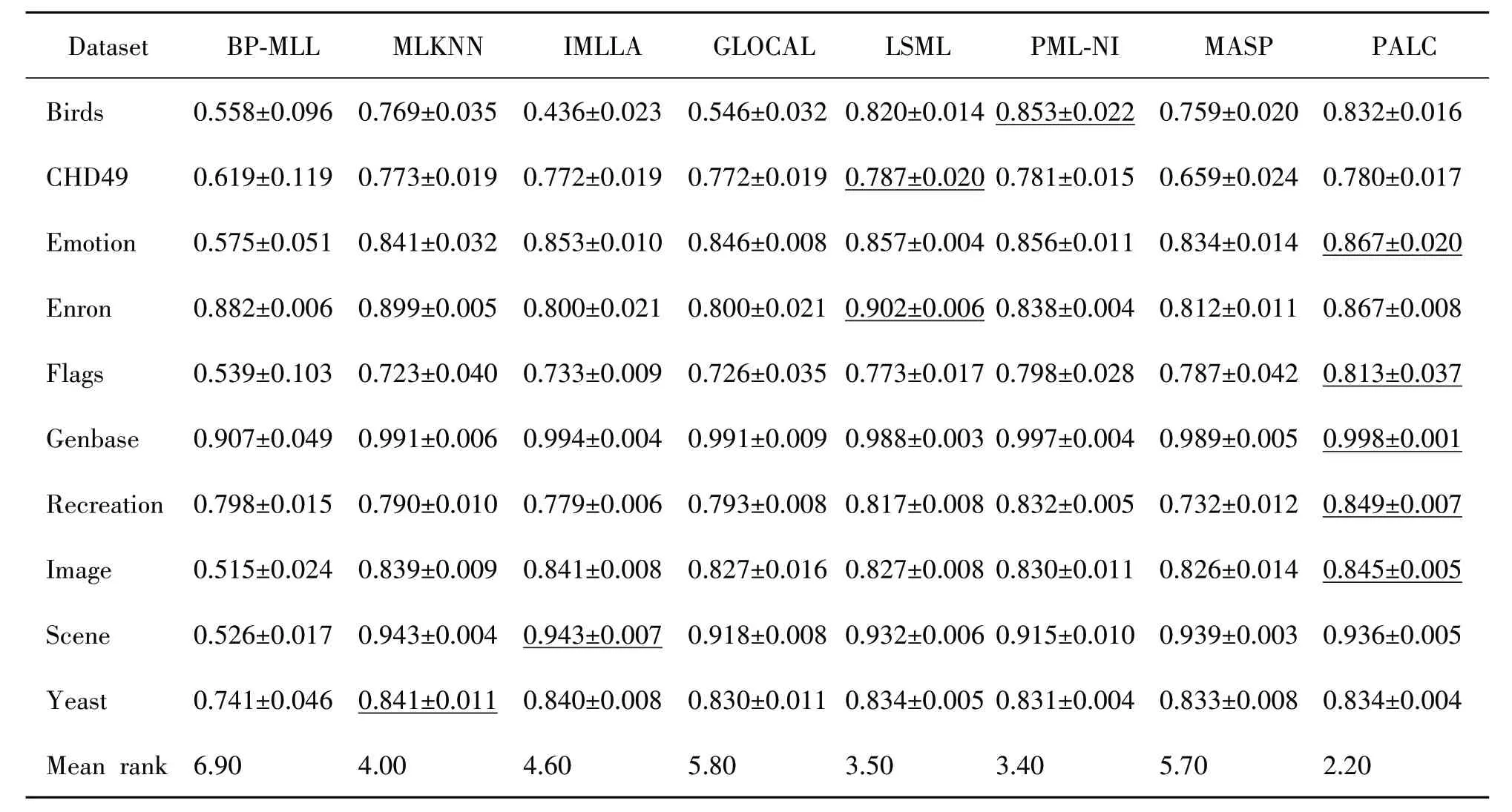
表3 对比实验在Micro-AUC指标下的结果

表4 对比实验在Peak F1指标下的结果

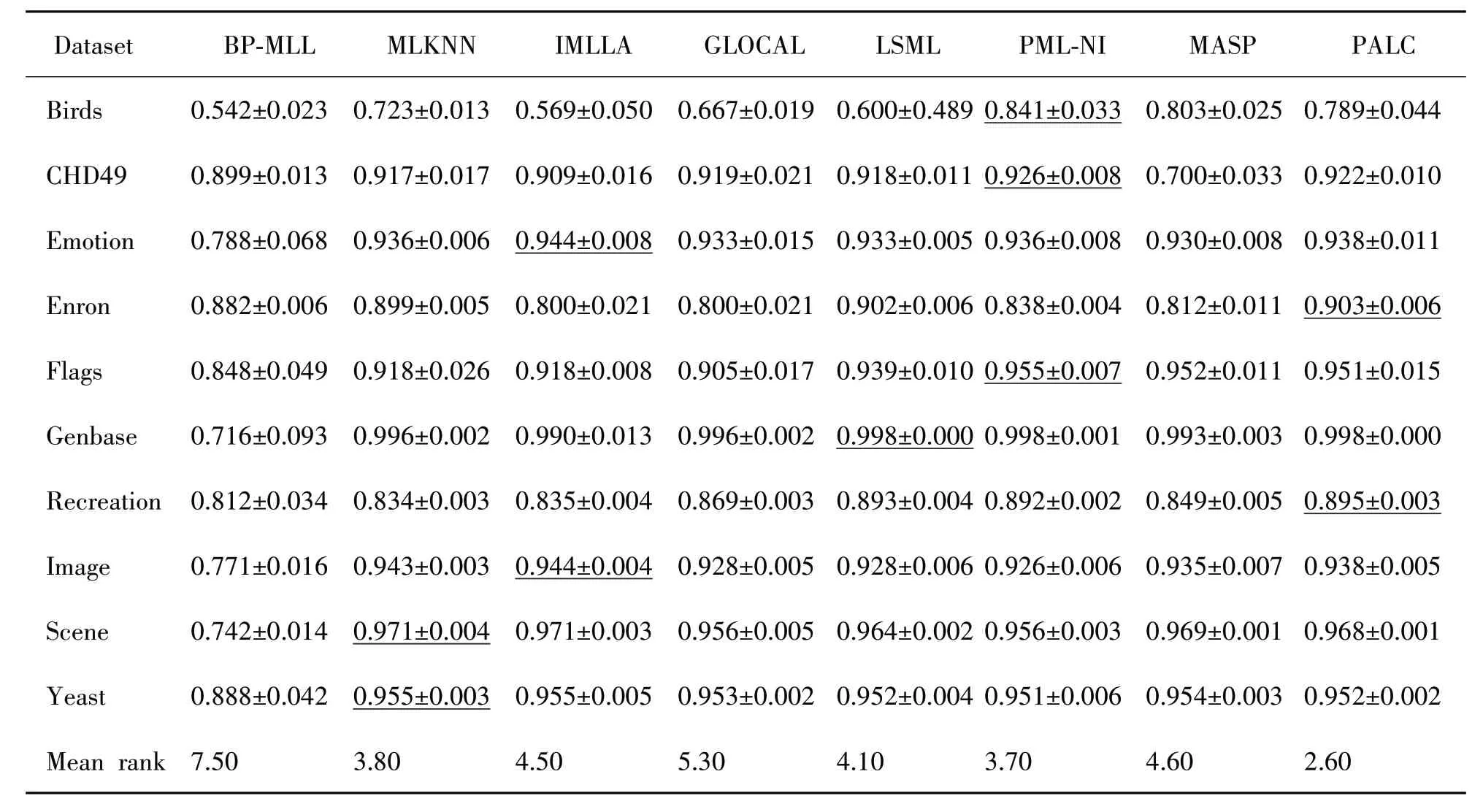
表5 对比实验在NDCG指标下的结果

根据表3～5的结果，可以明显看出PALC 在性能方面一直优于其余对比方法。具体来说，PALC 在Micro-AUC 和PeakF1得分方面表现出更好的平均性能。然而，对于NDCG 的性能差异没有统计学显著性。此外，所有评估的数据集在3 个评估指标上都表现稳定，没有明显波动。表明PALC 的性能在不同数据集上都是一致且可靠的。此外，研究结果表明，PALC在处理数据集密度时表现良好，显示了其在处理稀疏和稠密数据上的有效性。未来可以采用基于熵的多尺度决策表最优尺度选择策略[37］对特征预处理，以便消除噪声的影响。使用带属性偏好的模糊序决策信息系统的分配约简算法[38］可以有效提取特征，也能一定程度上减少噪声的影响，提高算法性能。

3.3 消融实验

为了验证PALC 的有效性，我们进行了消融研究。这些研究使我们能够系统地分析不同组成部分的影响或为了证明PALC 的优越性。图2 展示了PALC 与不考虑标签相关性的分类模型的比较结果，以及在相同正则下的网络模型和线性模型的消融研究结果。实验结果证明了融入标签相关性和利用串并神经网络对提高多标签分类的性能是有效的。

图2 不同组件下的消融实验结果

4 讨论

本研究提出的PALC 算法利用标签相关性和串并联网络来改进多标签学习预测。为了评估这些算法的性能，实验采用了Micro-AUC、PeakF1和NDCG 三个严格的评估指标。与现有最先进的方法相比，PALC算法在跨越不同领域的各种数据集上表现出优越的性能。此外，消融研究结果表明各个技术部件均能提高算法效果。然而，我们也认识到仍有一些方面需要进一步的研究和探索，例如本研究没有考虑特征中存在噪声以及缺失标签的情况。在未来的研究中，可进一步考虑采用更复杂的网络结构来提取特征问题，以及采用自适应标签相关性矩阵来正则化模型。

5 结论

设计了一种适合多标签的新型串行并行神经网络架构，在训练过程中可以有效捕获特征信息。并行网络对串行部分提取的共享特征进行补充，并增强了原始特征信息，从而在多标签分类任务中提高了性能。与常用的余弦相似度相比，本文提出的方法计算标签相关性更有效地考虑实际场景。最后将相关性矩阵通过流形正则化的方式融入神经网络，实现了与线性模型相比的性能改进并且双端口策略通过比较标签值实现了稳定的预测，增强了模型的可靠性和准确性。在实验中，PALC算法在10个数据集上进行了评估，结果显示其所有组件都是有效的。此外，PALC算法在5个来自不同领域的数据集上优于7个最先进的算法。