基于加权CML的城市综合客运枢纽脆弱性演化研究*

段晓红,许 葭,唐 静

(1.北方工业大学 经济管理学院,北京 100144;2.上海工程技术大学 城市轨道交通学院,上海 201620)

0 引言

城市综合客运枢纽在快速发展的同时,内在的脆弱性问题也逐渐凸显,对城市交通系统的安全稳定运行构成威胁。研究交通枢纽的脆弱性及其演化机理,对于科学精准地实施城市公共交通安全管理至关重要。

交通网络脆弱性研究最早见于道路交通,Berdica[1]将道路交通网络脆弱性定义为路网服务水平对于突发状况的敏感系数。对于轨道交通网络脆弱性,通常利用网络效率变化率加以衡量[2]。部分学者基于复杂网络理论对交通网络脆弱性研究进行拓展。许葭等[3]从脆弱性视角分析地铁网络事故扩散机理,并构建事故蔓延引力模型。李彦瑾等[4]以路网总阻抗的变化为指标衡量路网脆弱性。马超群等[5]利用客流有效路径子图和OD损失率指标分析城市轨道交通网络脆弱性。Szymula等[6]从客流和列车运行的角度构建混合整数规划模型,识别关键链路并评估铁路网络脆弱性。宋英华等[7]针对公共汽车和地铁双层网络,选取最大联通子图比例、网络连通效率和网络效率3个指标计算双层交通网络脆弱性。Hong等[8]以车站间的地理邻接程度表征城市公共汽车和地铁系统间的邻接关系,利用提供关键服务的最小行程时间和最小换乘时间度量公共交通系统脆弱性。部分学者将级联故障纳入研究范畴,Sun等[9]基于受影响乘客的出行行为分析,运用考虑级联故障演化的评价指标分析城市轨道交通脆弱性。Ma等[10]以客流量为权重构建公共汽车-地铁复合双层网络,并运用耦合映像格子模型模拟双层网络的级联失效场景。Lu等[11]将故障传播模式、车站抗风险能力和扰动指数相结合,构建改进的耦合映像格子模型,借此分析轨道交通网络级联故障过程。

但目前以城市综合客运枢纽为对象,从多线路互补的微观视角分析脆弱性演化机理的研究尚有不足。因此,本文拟以城市综合客运枢纽处的公共交通线路为分析节点,在探究线路脆弱性传递和演化机理的基础上,构建基于出行时间和成本的乘客替代线路选择模型,量化交通枢纽处线路脆弱性之间的影响系数,剖析脆弱性在交通枢纽处的传播和扩散路径,明确脆弱性协同治理和精准管控的关键线路和实施步骤,进而提高交通枢纽的本质安全水平。

1 城市综合客运枢纽系统脆弱性网络构建

运用有向复杂网络模型分析交通枢纽处脆弱性的传递效应,其关键在于明晰不同线路间的相互影响关系并量化影响程度。以往在多交通方式复合网络研究中,通常利用枢纽处交通站点间的距离或步行时间描述不同交通方式的邻接关系[7-8]。但事实上,在既定线路出现故障时,乘客对替代出行方式的选择更多地取决于其可能的出行目的地站点、使用替代方式到达目的地站点的时间、成本(票价)等因素。为此,本文将综合上述因素,利用节点影响力模型计算线路间的影响系数,建立城市综合客运枢纽脆弱性影响关系网络。

1.1 脆弱性影响关系网络模型

1.2 节点线路脆弱性影响力分析与度量

通过分析枢纽H处的线路i对其他线路j(j=1,2,…I,j≠i)的影响情况,确定影响系数wi,j。当线路i因扰动冲击而出现功能衰退时,原本由i承载的客流将向其他线路j转移,客流转移的条件是通过线路j能够到达线路i的双向下游站点ic(c=1,2,…,C)所覆盖的区域。故将ic纳入考察范围,比较乘客选择其他线路j前往ic的几率,线路j被选择的几率越大,则i对j的影响系数就越大。

根据节点影响力模型,网络中节点vj对vi的影响程度取决于两者间的最短路径长度和最短路径条数[12]。该模型由效率矩阵、待测节点矩阵和影响节点矩阵3部分构成。其中,效率矩阵从最短路径长度这一因素出发,分析vj对vi的影响;待测节点矩阵和影响节点矩阵则与最短路径条数相关。

实际上,线路i发生事故时乘客选择替代线路j前往站点ic的几率也与最短路径长度和最短路径条数相关:当通过线路j到达ic的路径长度越短时,越多的乘客将选择线路j;若途经线路j到达ic的路径数目越多,则乘客越容易到达ic,此时选择该线路的可能性越大。为此,将线路j视为影响节点,站点ic视为待测节点,引入多重影响力模型计算乘客选择j前往ic的几率。模型构建过程如下所示:

(1)

2)构建待测节点矩阵M[i]。待测节点矩阵从最短路径条数这一因素出发,计算从j到达ic的最短路径条数在所有线路g(g=1,2,…,i-1,i+1,…,I)到达ic的路径条数之和中所占的比例,该比例越高,则线路j被选择的几率越大。矩阵M[i]的元素如式(2)所示:

(2)

影响节点矩阵的元素计算从j到达ic的最短路径条数在j到达所有站点ih(h=1,2,…,C)的最短路径条数之和中所占的比例。此处无需比较从j前往不同ic几率的差异,故本文不考虑影响节点矩阵。

3)构建多重矩阵Z[i]。多重矩阵Z[i]由F[i]和M[i]加权求和获得,如式(3)所示:

Z[i]=α1×F[i]+α2×M[i],i=1,2,…,I

(3)

式中:α1=0.9,α2=0.1,均为利用层次分析法求得的权重[12]。

(4)

式中:β1=0.6,β2=0.4,均为利用德尔菲法获得的权重。

(5)

2 基于加权CML的交通枢纽系统脆弱性演化模型构建

2.1 加权耦合映像格子模型

加权耦合映像格子(CML)模型主要应用于研究复杂网络的动力学特征,能够反映交通网络中节点间的耦合作用机制和级联失效过程[14-15],本文运用CML模型描述交通枢纽系统脆弱性在级联失效过程中的扩散效应。目前,研究网络级联动力学的典型CML模型如式(6)所示:

(6)

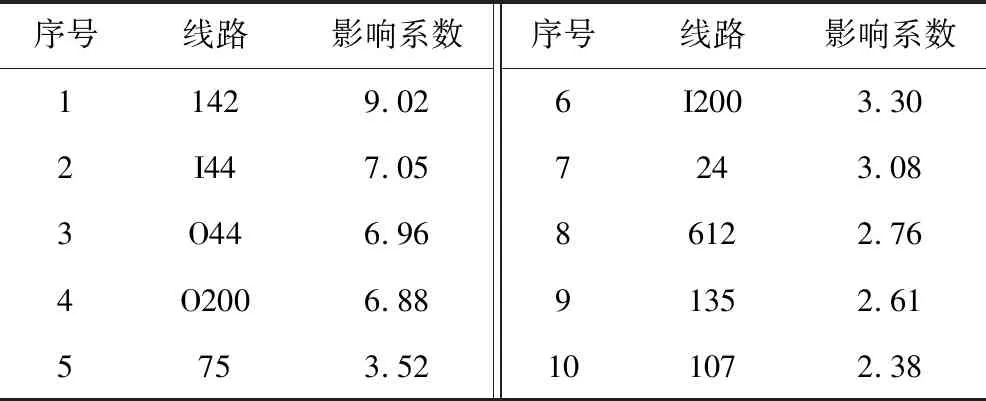
式中:Xi(t)为节点i在t时刻的状态,当0

在模拟网络中节点间的故障传播机制时,典型CML模型运用耦合系数ε反映故障节点对其他节点的影响程度,未区分因节点间连接强度不同而造成的影响程度差异。但事实上,若节点i对j的连接强度越高,i的脆弱状态越容易向j传播,i对j的影响越大。为更加合理地模拟本文加权网络的级联特征,借鉴Huang等[15]的研究方法引入边ei,j的权重wi,j对模型(6)进行改进,改进后的模型如式(7)所示:

(7)

2.2 交通枢纽系统脆弱性演化分析方法

在t时刻对交通枢纽H处的线路i施加扰动R,导致t+1时刻i的脆弱状态发生变化。在下一时刻t+2,与i存在互补关系的其他线路j将受到i在t+1时刻脆弱状态Xi(t+1)的影响。运用式(7)计算线路j在t+2时刻的脆弱状态值,若其值大于1,则j因容量超载而引发脆弱性凸显即出现故障,其所承载的客流又将在下一时刻转移至互补线路n并对n产生影响,以此类推,节点的脆弱状态可能随时间的推移发生扩散,这就形成脆弱性在枢纽处多条互补线路之间的传递和演化。

运用加权CML模型分析交通枢纽系统脆弱性演化过程的基本步骤如下:

步骤1:设置网络全部节点的初始脆弱状态值Xi(0)为(0,1)之间的随机值,选取1个网络节点施加外部扰动R≥1。

步骤2:统计上一时间步t全部节点的状态值,当节点状态值Xi(t)=0或Xi(t)≥1时,判定为失效节点,此时将该节点移除,并从t+1时刻起令其状态值Xi≡0。基于式(7)更新剩余网络节点的状态。

步骤3:重复步骤2,直至网络中失效节点个数不再变化,此时网络处于新的稳态。

步骤4:输出各个时间步的统计结果。

3 DZM交通枢纽脆弱性演化分析实证

本文以DZM交通枢纽为例,验证脆弱性演化模型的有效性。该枢纽集成地铁、城市轻轨、市区公共汽电车、市郊长途汽车、机场大巴等多维立体交通网络。

3.1 DZM交通枢纽脆弱性网络构建

DZM交通枢纽是多种运输方式的交汇点,选取存在互补关系的地铁、城市轻轨、公共汽电车作为研究对象。其中,地铁包含S21条线路;城市轻轨包含S13和SA2条线路;距离DZM地铁站500 m范围内存在5个公共汽车站,包含公共汽车线路36条。将上述各条线路抽象为节点vi,则交通枢纽脆弱性网络共有39个节点,节点线路名称如表1所示。

表1 线路名称Table 1 Names of lines

计算节点vi对vj(i,j=1,2,…,39)的影响系数,进而构建权重矩阵W=(wi,j)39×39。以线路S2为例,描述影响系数的计算过程。

表2 S2对其他线路的影响系数排名前10Table 2 Top 10 lines ranked by influence coefficient of S2 on other lines

同理,计算39条线路两两间的影响系数,得到网络的权重矩阵,进而构建DZM交通枢纽脆弱性网络模型如图1所示。图中节点大小取决于点出度值,线条粗细与边的权重值相关。运用Gephi软件的社区探测算法将39个节点划分为3个子群,图1中颜色相同的节点属于同一子群。网络全局特征指标如表3所示。

图1 DZM交通枢纽脆弱性网络Fig.1 Vulnerability network of DZM transport hub

表3 交通枢纽脆弱性网络全局特征指标Table 3 Global characteristic indicators for vulnerability network of transport hub

由表3可知,网络密度为0.379 0,网络直径为4.000 0,表明网络中节点间存在较多直接联系,且任意点对之间最多间隔3个节点;网络平均路径长度为1.701 0,平均聚类系数为0.600 0,说明网络具有较短的平均路径长度和较高的聚类系数,该网络呈现出“小世界”特性。

3.2 DZM交通枢纽脆弱性演化过程分析

根据加权CML模型,当耦合系数ε、节点出强度Q和外部扰动R不同时,交通枢纽脆弱性的演化过程表现不同。其中,ε决定脆弱性的扩散速度,Q决定节点脆弱性在网络中单步传播的难易程度,R则直接影响系统脆弱性传播的广度和深度。为此,选取出强度排名前4的节点线路(包括线路980、404、132和418)进行蓄意攻击,并根据模型测试结果将耦合系数划分为0.1、0.4、0.7 3个等级,外部扰动划分为2、5、8 3个等级,观察不同参数组合下失效节点线路数目随时间的变化过程。图2所示为线路980和404遭受攻击后,DZM交通枢纽脆弱性的演化过程。

图2 线路脆弱性的演化过程Fig.2 Evolution process of line vulnerability

由图2可知,同一节点遭受攻击时,随耦合系数和外部扰动强度的增大,DZM交通枢纽线路脆弱性的级联效应明显增强,受影响节点数目显著增多。当耦合系数为0.7、外部扰动为5时,4条测试线路被攻击后的6个时间步内DZM枢纽处的39条线路均受到影响。节点出强度与脆弱性级联效应的相关性不明显,原因是节点强度仅关注脆弱性在单步内的传递程度,而级联效应与多步内的影响效果相关。

设置ε=0.4,R=5,对39条线路分别进行蓄意攻击,统计稳态时受影响节点线路数目和时间步数,结果如表4所示。

表4 不同线路被攻击时的脆弱性扩散后果Table 4 Diffusion consequences of vulnerability of different lines under attack

由表4可知,S13、S2、142、980、O200、135、418、F852线路被攻击后,全部39条线路将遭受影响和威胁,达到新的稳态所需时间步数为6～8步。

为剖析交通枢纽脆弱性的扩散路径,统计线路被攻击后的各个时间步内网络中受影响线路的分布情况,以线路404为例,其脆弱性扩散路径如表5所示。

表5 线路404脆弱性的扩散路径Table 5 Diffusion path of vulnerability of line 404

由图1可知,线路404与132、401、413、416等14条线路属于同1个子群,由表5可知,其中12条线路在404被攻击后的2个时间步内受到影响。因此,线路404脆弱性的演化路径与交通枢纽脆弱性网络的子群分布存在一致性。

4 结论

1)乘客替代线路选择和多重影响力模型的计算结果符合公交线路之间的实际互补耦合情况。如线路S2对线路142、I44、O44、O200等的影响最明显,当DZM枢纽处的线路S2呈现脆弱状态时,需加强对这些互补线路的监测和控制。

2)根据DZM交通枢纽脆弱性网络全局特征分析,该网络呈现“小世界”特性,枢纽处39条线路之间的联系紧密且连通性强,网络结构决定脆弱性易于在节点线路之间传递和扩散。

3)基于脆弱性影响系数的加权耦合映像格子模型适用于分析线路脆弱状态对整个交通枢纽的影响范围、过程及后果。线路S13、S2、142、980、O200等是DZM交通枢纽的关键节点线路;线路404的脆弱状态将通过7个阶段和层级的传播,最终扩散至38条线路。交通枢纽运营管理部门应优先监控关键节点线路的脆弱性,同时,根据脆弱性的扩散过程对其他线路实施分阶段协同管控。