基于智能图像识别的轨道交通钢轨焊接接头识别*
吴泽宇 王文斌 魏志恒 朱 彬 李明航
(1.中国铁道科学研究院, 100081, 北京; 2.中国铁道科学研究院集团有限公司城市轨道交通中心, 100081, 北京∥第一作者, 硕士研究生)
基于神经网络的图像识别技术能够提取不同图像的特征信息,从而实现对图像的区分及识别。文献[1]提出了AlexNet网络结构模型,并以其优异的图像识别能力赢得了当年的ILSVRC(ImageNet大规模视觉识别挑战赛)冠军,自此CNN(卷积神经网络)成为了图像识别的核心算法模型。该算法将时频分析技术与图像识别技术相结合,实现对信号的有效分类。文献[2]采用Gramian角场和Markov转移场将时间序列信号编码为图像,通过平铺CNN模型对时间序列图像进行分类;文献[3-4]通过使用递归图将时间序列转换为二维纹理图像,并分别采用支持向量机和深度神经卷积网络对其进行分类。文献[5]通过采集运营列车的轴箱以及车体其他部件的加速度实现对钢轨的动态检测;文献[6-7]从能量角度分析了车辆轴箱振动加速度信号,通过对加速度信号有效值的量纲一化处理获得轨道冲击指数,以对轨道短波不平顺进行描述。本文以北京地铁19号线实测数据为基础,采用小波变换提取钢轨焊接接头的时频信息,并应用AlexNet CNN技术对时频信息进行区分,以实现对钢轨焊接接头的识别;通过计算轨道冲击指数与钢轨表面不平顺的滑动峰峰平均值,评价钢轨焊接接头对车辆动力学的影响。
1 轨道交通钢轨焊接接头识别方法原理
1.1 AlexNet CNN模型
CNN的工作原理受哺乳动物视觉过程的启发而来,是一种前馈形神经网络,在图像识别、视频分析、声音识别、自然语言处理等领域取得了巨大的突破。CNN通常由5层构成,分别是输入层、卷积层、激活层、池化层及全连接层。其中:输入层负责数据的预处理操作;卷积层通过卷积提取图像特征,并降低噪声;激活层对卷积层的输出结果进行非线性映射,避免每层的输出仅是输入的线性组合;池化层又称下采样层,即在保留有效信息的前提下,减少数据量和计算量,并加强图像特征的不变性;全连接层通常位于数个卷积层/采样层的组合之后,在整个CNN架构的末端位置,也称稠密层,其作用相当于一个普通的分类器。
AlexNet作为一种经典的早期CNN模型,由Alex Krizhevsky设计[1],包括:输入层1个,卷积层5个,全连接层3个。其中,对全连接层进行了最大池化。AlexNet CNN结构模型[1]如图1所示。
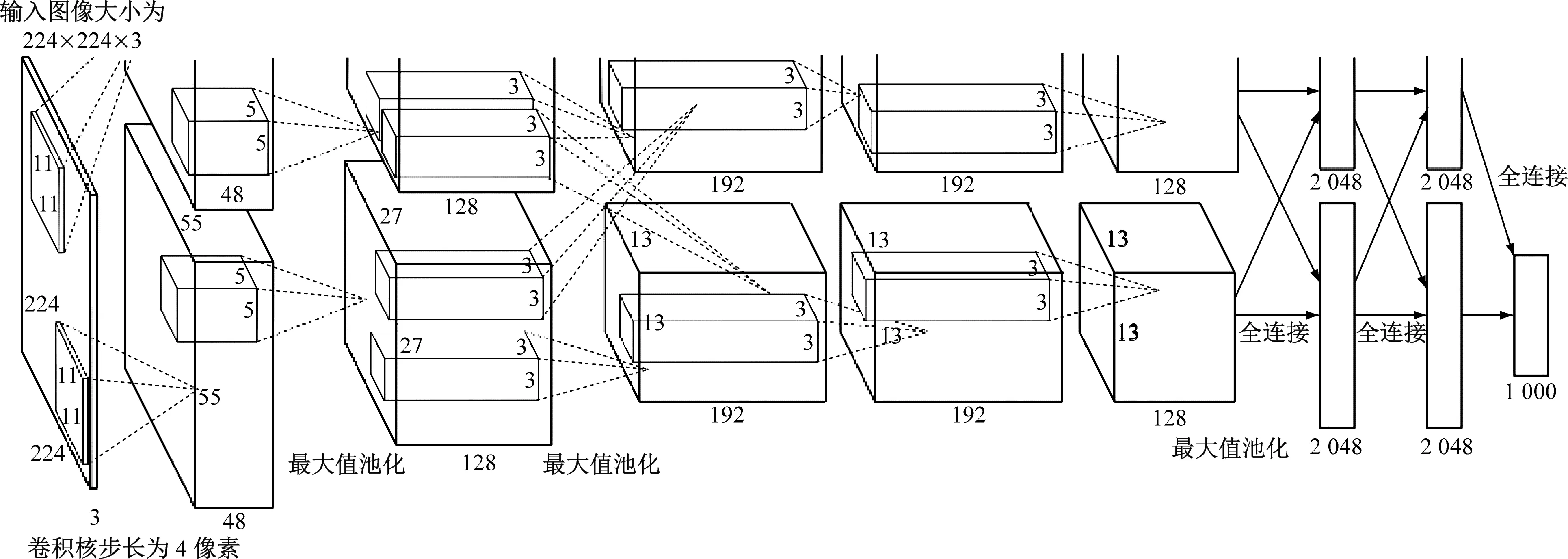
注:图中长方体侧边的数字为各卷积层与池化层中的卷积核与池化核尺寸及通道数。如:224×224×3中,224×224表示图像的宽度和高度,单位为像素;3表示图像的通道数。
1.2 小波变换
为获得一组信号的频率成分,通常采用傅里叶变换将信号从时间域转换到频率域,但傅里叶变换只能获取一段信号总体上频率成分的组成,以及缺失的各频率成分出现的时间信息;此外傅里叶变换只适用于确定性的平稳信号[8],即仅对信号中突变易解释成一系列低成分的高频信号叠加。为避免此种问题的出现,通常对给定的时间序列信号x(t),采用时频分析方法提取信号的频率信息。常用的时频分析方法包括短时傅里叶变换、小波变换、Wigner-Ville分布等。其中小波变换已成为目前处理非平稳信号最重要的手段之一。
定义1个平方可积的小波母函数ψ(t),对其作平移和伸缩变换,得到小波基函数ψa,b(t):
(1)
式中:
t——时间;
a——伸缩因子;
膀胱爆炸损伤程度可由黏膜损伤至膀胱破裂,黏膜损伤者留置尿管即可。膀胱破裂者,如镜下见裂口通向腹腔或裂口较大伴活动性出血,应立即手术修补,并检查邻近肠道有无损伤。如为腹膜外损伤,破口较小且无活动性出血,可行保守治疗,保证尿液引流通畅。爆炸所致膀胱裂口常不规则且多发,修补时应仔细。
b——平移因子。
式(1)中,若a、b不断变换,可得到一族小波基函数ψa,b(t)。对于给定的二次可积信号x(t),有连续小波变换:
(2)
实际信号处理过程中,往往需要将尺度和位移离散,采用离散小波变换进行时频分析,通常采用二进离散小波变换。对于给定的信号x(n),令:a=2j,b=2jk,j∈Z,k∈Z,则离散小波变换wx(2j,2jk)为:
(3)
1.3 轨道冲击指数计算方法
提取运营列车的振动加速度信号,并采用惯性基准法对轨道状态进行检测的方法早已被广泛接受并验证[5,9]。车辆轴箱振动加速度是轮轨耦合作用的结果,基于轴箱振动加速度的轨道不平顺检测往往受多种因素的影响。文献[10]证明了车轮不圆顺对基于惯性基准法测得的轨道不平顺数据在频域方面影响较大,此外,车轮踏面、钢轨材料、车辆悬挂参数及钢轨廓形等因素均可能对不平顺检测结果造成影响。文献[6]从能量的角度描述轮轨冲击引起的轴箱振动加速度的高频特性,提出采用轨道冲击指数描述轨道短波不平顺状态。
对于给定的滤波后加速度信号集合{xi|i=1,2,…,N}(N为加速度信号波形点数),计算其有效值,得到集合{Sr|r=1,2,…,N-K+1}。其中,K为计算窗长,Sr为:
(4)
(5)
2 轨道交通钢轨焊接接头识别分析
2.1 钢轨焊接接头样本挑选及时频图构建
提取北京地铁19号线某运营列车的轴箱振动加速度信号,如图2所示。

a) 整体图
显然,钢轨焊接接头对应的轴箱垂向振动加速度信号在时域上有两个较为明显的特征:①两个冲击信号相隔25 m,为单根钢轨长度;②钢轨焊接接头会造成一大一小两个冲击,冲击相隔2.2 m,为转向架轴距,其中,大冲击为钢轨焊接接头对传感器所在轮对的冲击,小冲击为后一轮对在经过钢轨焊接接头时对前一轮对传感器所造成的冲击。对不同运营里程处的钢轨焊接接头加速度信号进行小波变换,得到如图3 a)所示的加速度信号时频图。与图3 b)所示的非钢轨焊接接头时频图相比,图3 a)所示的加速度信号时频图中钢轨焊接接头信号在时频域上为明显的两点式特征,两点呈现出一明一暗;查看不同程度的钢轨焊接接头信号,发现其频率分布范围基本一致。由此为AlexNet CNN模型识别钢轨焊接接头提供了条件。

a) 钢轨焊接接头
2.2 钢轨焊接接头识别
挑选200组钢轨焊接接头及非焊接接头时频图作为训练样本,通过人工打标签。采用已经预训练的AlexNet模型,修改输出参数设置。上述200组样本中,70%用于训练,30%用于校正。对AlexNet模型重新训练,得到一个能够识别轨道短波病害作用下的轴箱振动信号新模型。AlexNet模型训练的准确率与损失随迭代次数变化曲线如图4所示。由图4可见,最终模型的验证准确度达到了92.98%。

a) 准确率
针对已训练好的模型,另选取100组钢轨焊接接头和非钢轨焊接接头数据,获取其时频图并对其进行识别,共重复3次,其识别准确率与验证准确度相一致。
3 钢轨焊接接头不平顺幅值变化对其表面不平顺的影响
使用波磨小车对北京地铁19号线某上行普通轨道区段钢轨表面不平顺进行检测,共得到两段钢轨表面不平顺实测波形,如图5所示。

a) 第1段
为去除图5实测结果中钢轨焊接接头不平顺幅值中较大的脉冲,对钢轨表面不平顺波形进行多次不同带宽的带通滤波。对比滤波结果可发现,30~100 mm的带通滤波结果(见图6)会出现分布较为均匀的钢轨表面不平顺滑动峰峰平均值峰值,且每个峰值的间距约为25 m。钢轨焊接接头长度通常不超过11 mm,且每两个焊接接头之间的距离通常固定为25 m,其里程特征与带通滤波后的钢轨表面不平顺的滑动峰峰平均值峰值分布特征相似。此外,由于焊接技术的不稳定、焊接材料存在缺陷等众多因素的影响,钢轨焊接接头所在里程处存在较大的不平顺,这也与图6中分布较为均匀的滑动峰峰平均值峰值远大于相邻区域内其他里程处滑动峰峰平均值的特征相符。因此,可认为图6中较为均匀分布的钢轨表面不平顺滑动峰峰平均值峰值为钢轨焊接接头所对应的滑动峰峰平均值。
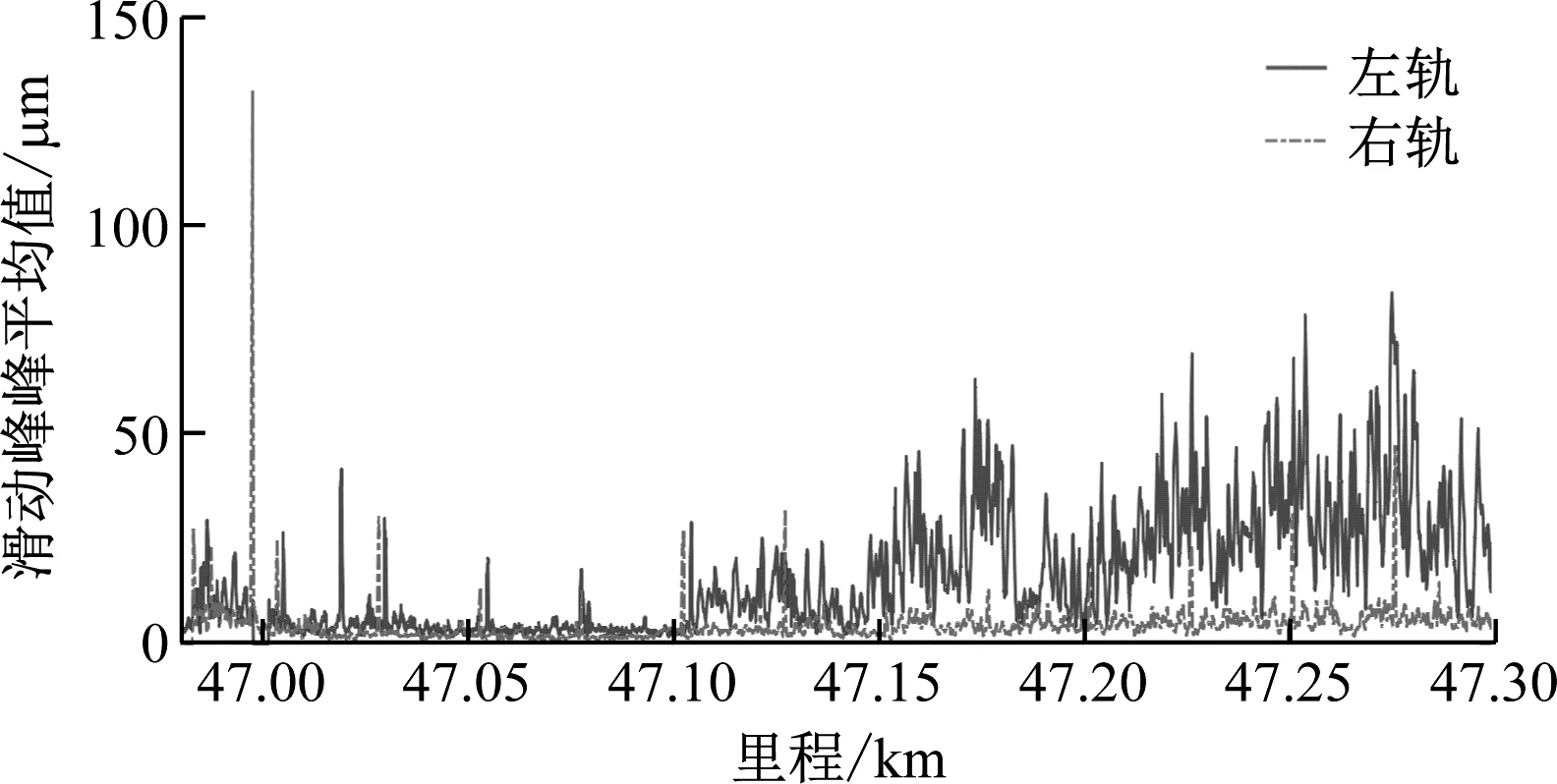
a) 第1段
提取运营列车轴箱垂向振动加速度,根据式(4)及式(5)计算轨道冲击指数,得到如图7所示的计算结果。由图7可以看出,轨道冲击指数与经30~100 mm滤波的实测钢轨表面不平顺滑动峰峰平均值的波形存在一定程度的相似性。此外,轨道冲击指数具有与钢轨表面不平顺滑动峰峰平均值相似分布特征的峰值,在运营里程上与钢轨焊接接头相对应,说明列车在通过钢轨焊接接头时轴箱产生了较大的垂向振动加速度,进而导致轨道冲击指数的计算值出现了明显的尖峰。

a) 第1段
统计每处钢轨焊接接头对应的钢轨表面不平顺滑动峰峰平均值与轨道冲击指数,以钢轨表面不平顺滑动峰峰平均值为自变量,轨道冲击指数为因变量,剔除部分异常散点并拟合曲线,结果如图8所示,其中黑色散点表示不同滑动峰峰平均值下的轨道冲击指数。由图8可见:轨道冲击指数随钢轨表面不平顺滑动峰峰平均值增长呈先减小后增大的趋势;当钢轨表面不平顺滑动峰峰平均值大于20μm时,轨道冲击指数随其增大而缓慢增长,这说明钢轨焊接接头一定程度上会对基于轨道冲击指数的不平顺检测方法产生影响,但二者之间并不呈正相关关系。

图8 轨道冲击指数-钢轨表面不平顺滑动峰峰平均值拟合曲线
4 结语
1) 钢轨焊接接头在列车轴箱振动加速度信号中存在较为明显的空间域分布特征与时频特征。其中:空间域分布特征表现在每两个钢轨焊接接头信号之间的间距为25 m,且每个信号由间距为2.2 m的两个尖峰所构成;时频特征表现为钢轨焊接接头所在里程附近有一明一暗两个亮点。上述特征清晰明了,使AlexNet CNN能很好地从大量的轴箱振动加速度信号中拾取钢轨焊接接头所在里程,本文AlexNet模型的识别准确率约为92.98%。
2) 钢轨焊接接头不平顺滑动峰峰平均值对基于轨道冲击指数的短波不平顺检测结果有一定的影响,钢轨焊接接头处的轨道冲击指数通常随钢轨表面不平顺滑动峰峰平均值的增大而呈现一种先减小而后缓慢增大的趋势,并不具有正相关性。

