射流清管器环状喷嘴流场模拟及优化设计
李亚茜 田 园 阴丽诗 陈界学 谢 晶
1. 中国石油化工股份有限公司西南油气分公司采气四厂, 重庆 402160;2. 重庆科技学院石油与天然气工程学院, 重庆 401331;3. 中国石油西南油气田公司重庆气矿, 重庆 400700
0 前言
天然气管输过程中,由于气源、过滤系统、运行年限等原因,管道内壁易附着以粉尘为主的大量污物,致使管道有效流通面积缩减,降低了管输效率[1-3]。射流清管器可有效清除管道内污垢,提升管输效率,保障天然气输送安全[4]。射流清管器喷嘴结构对流场特性有显著影响,是实现射流功能的关键部位,其射流效果的优劣直接决定了清管工作效率[5],因此选择和设计合理的喷嘴结构非常重要。
射流清管器多用于清管速度控制及防止段塞流捕集器过载,对于射流控制及射流清管器喷嘴结构的研究主要集中在旁通率自动调节方面。目前广泛使用的射流清管器主要有3种喷嘴结构:直通型、前端带折流板型、内设阀门型[6-7]。对于天然气管道内壁附着的粉尘和固体杂质,目前常用的各种喷嘴结构均不能达到最佳吹扫效果。调研发现环状射流对管道内壁粉尘携带效果最佳,吹扫范围最大且吹扫效果均匀[8-10],目前环状喷嘴多用于取芯钻进及反循环钻探中。取芯钻进中环状喷嘴由环状分布的多个单喷嘴组成,通过喷嘴流场模拟射流对冰层的作用过程来优化设计环状喷嘴的喷射角度、单喷嘴的排列方式;反循环钻探中环状喷嘴为直通环形结构,通过模拟环状喷嘴内流场反循环的形成过程来优化设计环状喷嘴间隙、高度、喷射角度。因此,为充分发挥环状喷嘴的射流吹扫作用,实现高效、安全、可控的清管过程,需对其几何结构参数进行优化。
基于射流流动理论和计算流体力学(Computational Fluid Dynamics,CFD)仿真分析法,选用实际气体模型开展射流清管器环状喷嘴射流过程的数值模拟。通过改变环状喷嘴内锥角和外锥角的大小,根据不同结构参数下流速和湍流动能在下游管道中的变化情况,探索最大化喷嘴吹扫效果的最优结构参数,为环状喷嘴结构优化设计提供理论依据。
1 模型建立与网格剖分
1.1 模型建立
射流清管器环状喷嘴的轴心部分留有可调节射孔,以便调节旁通率,主要由水平段和扩散段组成,其中直接影响射流效果的是扩散段参数[11],因此重点关注扩散段参数的优化,环状喷嘴结构见图1。以Φ273×10 mm的天然气管道为例,由于环状喷嘴几何结构只对清管器前端的下游流场产生影响[12],即清管器后端流场特性不影响喷嘴结构参数的优化,因此建立模型时可将其略去[13-14],计算区域只包括射流流场,见图2。图2中区域Ⅰ、Ⅱ分别表示环状喷嘴、射流流场,将区域Ⅱ左端面与管轴的交点设为坐标原点O,管轴设为X轴,区域Ⅱ左端面为Y轴。为得到区域Ⅱ中流速和湍流动能的变化规律,应选择环状喷嘴后10倍管径为计算区域,但考虑到射流的充分发展区域范围远小于10倍管径,基于环状射流二维轴对称简化模型计算结果,将模拟计算区域长度设置为650 mm。
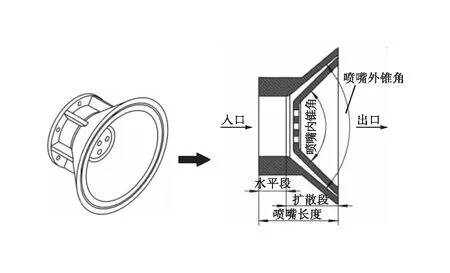
图1 环状喷嘴结构示意图
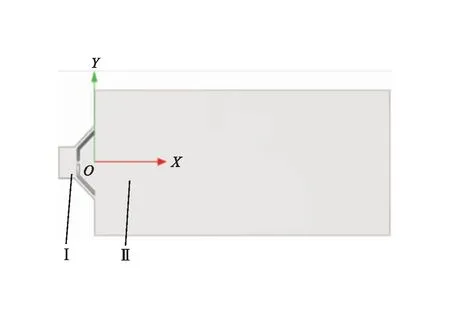
图2 环状喷嘴射流计算区域模型图
1.2 网格剖分
应用Ansys ICEM软件进行结构化网格划分,见图3。由于环状射流区域的流速、湍流动能等流动参数变化剧烈,因此针对该区域进行局部网格加密,为了使网格的疏密能更好地适应流场的变化,在初算后依据计算结果进行了网格自适应处理。经网格无关性验证,摒除了网格密度对计算结果的影响,最终确定射流流场网格节点数为 312 787,单元数为303 352,六面体网格最小雅克比矩阵与最大雅克比矩阵比值均大于0.6,满足计算精度要求。
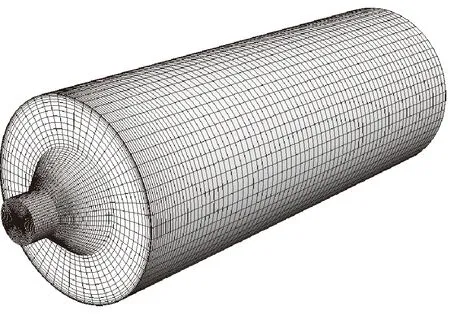
a)网格划分整体情况
1.3 求解过程
由于射流速度远低于音速,不属于强可压缩流动范畴,故采用Fluent软件自带的基于压力的耦合求解器进行求解[15]。由于天然气经过射流喷嘴高速喷射时会导致温度变化,考虑到温度对黏度的影响,因此气体黏度采用反应气体黏温关系的Sutherland模型模拟;流动介质选用甲烷,密度计算选用P-R状态方程;考虑到环状射流与轴心射流相互扰动造成流线弯曲,选用RNGk-ε湍流模型,壁面采用增强壁面函数,计算得到y+均在1.2~5.3之间。设置收敛临界值为1×10-5,计算得到出口与入口质量流量相对误差为0.65%,计算收敛。
2 环状喷嘴扩散段参数优化
采用喷嘴长度、喷嘴内锥角、喷嘴外锥角来表征环状喷嘴扩散段几何结构。由于清管器最大转弯半径及环状喷嘴重量对清管器骨架重心偏移的影响[16-18],限定了Φ273×10 mm的天然气管道射流清管器最大环状喷嘴长度为78.5 mm,同时环状喷嘴在清管器骨架上所需的最小安装空间限制了环状喷嘴水平段最小长度为41 mm,故环状喷嘴扩散段长度设计采用37.5 mm。为得到具有最佳管道内壁吹扫能力的环状喷嘴内锥角和外锥角的大小,需依据环状喷嘴在不同结构参数下的射流吹扫效果[19],从径向和轴向维度选取多个剖面对射流流场区域速度和湍流动能的覆盖范围及变化规律进行分析,径向剖面和轴向参考线选取见图4。轴向截取距离环状喷嘴出口为50 mm、100 mm、150 mm、200 mm、250 mm 的5个圆形剖面,见图4-a);径向以管轴为原点、沿管道半径分别取0 mm、60 mm和110 mm代表管道轴线、中间层、近壁层3个位置,见图4-b)。
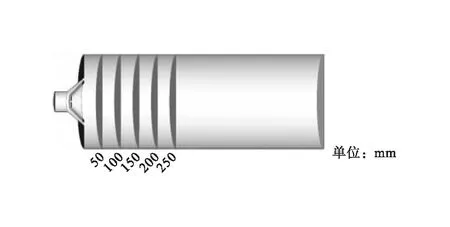
a)沿管道轴线的5个圆形剖面
2.1 内锥角优化
为确定最优内锥角,固定环状喷嘴入口直径55 mm,水平段长度41 mm,扩散段长度37.5 mm,同时设置外锥角大小与内锥角大小相同,避免外锥角对射流流场的影响,达到分析单一变量的目的。共设置了70°、80°、90°、100°这4种不同内锥角的优化方案,并将4个模型分别编号为A1、A2、A3、A4。
2.1.1 内锥角对射流流场区域流速的影响
射流吹扫速度越大,气体携带颗粒的能力越强,因此可用于评价对粉尘、固体杂质等污垢的吹扫效果。不同内锥角下环状喷嘴不同剖面流速云图见图5。由图5-a)可知:射流束的外表面存在扩散现象,并沿管道径向发散。区域Ⅱ中的高速流核区呈现锥形,形成的轴心射流束可冲散管道轴线附近堆积的污垢,同时轴心锥形射流与环状射流相互扰动形成涡旋,将管壁附着的粉尘、固体杂质卷入射流流场,使之变为悬浮状态并被射流气体携带向前运动。由图5-b)可知:各模型圆心附近流速达到最大,沿管道半径存在明显的梯度变化,而径向剖面的流速分布差别很小,但随着距离增加,内锥角大的模型衰减速度更慢,这是因为随着内锥角增大,环状射流效应增强,射流吹扫管壁产生的涡旋对轴心射流的抑制作用减弱。模型A4与模型A3的流速分布云图和衰减速度近乎一致,说明继续增大内锥角对管内流速分布的影响效果已不明显。
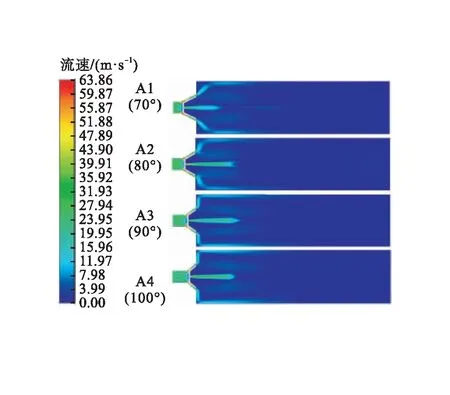
a)轴向剖面
不同内锥角下环状喷嘴不同位置的流速变化曲线见图6。由图6可知,各模型均在400 mm处衰减至管道的平稳输送速度,说明环状射流吹扫范围与内锥角大小无关。管道轴线上管道长度0~138 mm内,速度随内锥角增大而增大,其中模型A3和模型A4流速相差不大,略高于模型A2流速,显著高于模型A1流速;管道长度138 mm之后模型A3流速始终高于模型A4流速。中间层上各模型流速变化情况基本一致,管道长度0~46 mm内流速均迅速衰减,其中模型A3流速最大;管道长度 46 mm 之后模型A4流速最大。近壁层上管道长度0~200 mm内,当内锥角从70°增大到90°时,速度有一定程度的增加;但当内锥角增大到100°时,其流速曲线与90°时流速曲线几乎重合,流速不再增大;管道长度200 mm之后模型A3的流速反而高于模型A4流速,说明90°的内锥角是流速变化的临界值。综上,模型A3在管道轴线和近壁层上的流速最大,仅在中间层上略小于模型A4流速,因此内锥角为90°的模型A3在流场中具有最优的吹扫速度分布。
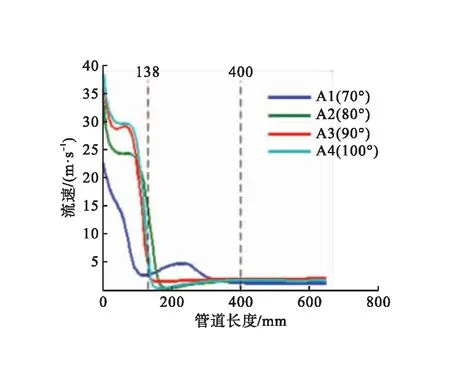
a)管道轴线
2.1.2 内锥角对射流流场区域湍流动能的影响
湍流动能反映了湍流脉动速度的大小,湍流动能越大,射流对管内污垢的扰动能力越强,可作为评价射流效果的重要指标[20]。不同内锥角下环状喷嘴不同剖面湍流动能云图见图7。由图7-a)可知:湍流动能较大区域基本与高速流核区相吻合,各模型的湍流动能在管道轴线上最大,在中间层上最小。由图7-b)可知:模型A3和模型A4在整个径向剖面内湍流动能覆盖区域较大,且沿管道轴线衰减速度较慢,在距离环状喷嘴出口250 mm处的近壁层仍有较大值,能保持对管内污垢较强的扰动,有利于将其卷入射流核心区。
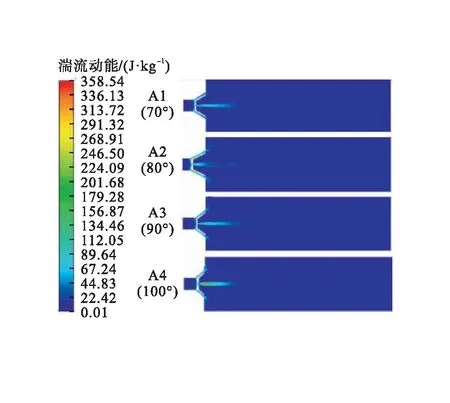
a)轴向剖面
不同内锥角下环状喷嘴不同位置的湍流动能变化曲线见图8。由图8可知:各模型的湍流动能均在管道长度400 mm处趋于稳定的低值状态。内锥角大小对管道轴线上的湍流动能影响明显,管道长度0~98 mm内模型A3的湍流动能呈急剧减小的趋势,其湍流动能始终高于其他模型湍流动能。中间层上各模型的湍流动能均在喷嘴出口处达到峰值,随后各模型的变化情况基本一致,但总体上模型A3的湍流动能略大于其他模型湍流动能。近壁层上模型A1由于内锥角小,射流流线与管内壁接触点靠后,流体微团从喷嘴出口运动到壁面的距离大,黏性耗散多,因此湍流动能始终低于其他模型湍流动能;在管道长度0~217 mm的较大范围内,模型A3的湍流动能显著高于其他模型湍流动能。综上,内锥角为90°的模型A3在管道轴线、中间层、近壁层3个位置的湍流动能分布情况最好。

a)管道轴线
综合考虑流场中流速、湍流动能的变化情况,确定射流清管器环状喷嘴的最优内锥角为90°。
2.2 外锥角优化
设置内锥角为90°,其他参数不变,在固定旁通面积的基础上设置75°、80°、85°这3种不同外锥角的优化方案,并将3个模型分别编号为B1、B2、B3。
2.2.1 外锥角对射流流场区域流速的影响
不同外锥角下环状喷嘴不同剖面流速云图见图9。由图9可知:各模型在区域Ⅱ中高速流核区的变化规律与覆盖范围相似,差别较小,难以看出射流流速在数值上的差别,因此需从管道不同位置的流速变化曲线来进一步分析外锥角对射流流速的影响规律。
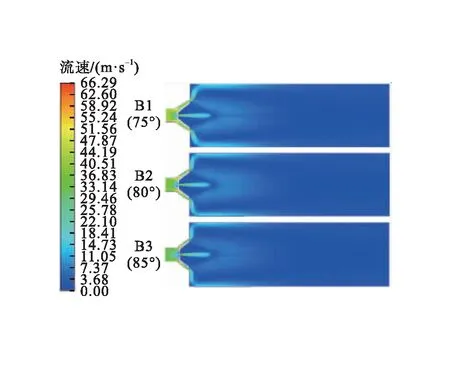
a)轴向剖面
不同外锥角下环状喷嘴不同位置的流速变化曲线见图10。由图10可知:各模型流速均在管道长度 600 mm 处达到稳定值。管道轴线上各模型的流速变化曲线几乎重合,管道长度0~79 mm内各模型流速均呈逐渐减小趋势,管道长度79 mm之后由于环状射流对轴心射流的扰动,轴线上流速均先增大后减小,在管道长度130 mm左右达到峰值,其中模型B2的流速略大于其他模型流速。各模型在管道中间层上的流速曲线几乎重合,差别很小。管道近壁层上的流速呈先增大后减小的趋势,在管道长度0~26 mm内,各模型流速几乎一致,随后模型B3在管道长度53 mm处流速达到峰值12.4 m/s,模型B1在管道长度61 mm处流速达到峰值14.1 m/s,模型B2在管道长度72 mm处流速达到峰值14.5 m/s,且模型B2流速始终高于其他模型流速。综上,3种模型在管道轴线和中间层上的差别很小,在近壁层上的流速变化规律基本一致,其中模型B2在近壁层上优势明显,因此外锥角为80°的模型B2具有最优的吹扫速度分布。
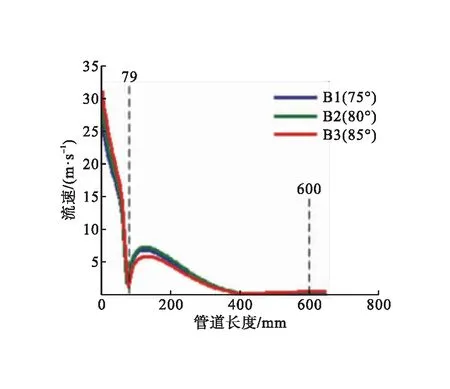
a)管道轴线
2.2.2 外锥角对射流流场区域湍流动能的影响
不同外锥角下环状喷嘴不同剖面湍流动能云图见图11。由图11可知:各模型在区域Ⅱ中湍流动能分布情况相似,均能在较大范围内保持较高的湍流动能,并沿管道轴线缓慢衰减,其中模型B2的湍流动能在距离喷嘴出口200 mm处的近壁层仍有较大值。

a)轴向剖面
不同外锥角下环状喷嘴不同位置的湍流动能变化曲线见图12。由图12可知:各模型的湍流动能均在管道长度600 mm处趋于稳定的低值状态。各模型在管道轴线和中间层上的湍流动能变化曲线基本重合,在管道中间层管道长度98 mm之后,模型B3湍流动能略低于其他模型湍流动能。近壁层上模型B1和模型B2在管道长度0~59 mm区间内湍流动能曲线几乎重合,且湍流动能均大于模型B3湍流动能;管道长度59~600 mm内,模型B2湍流动能大于其他模型湍流动能。综上,各模型在管道轴线和中间层上差别不大,近壁层上模型B2优势明显,因此外锥角为80°的模型B2在流场中具有最佳的湍流动能分布。
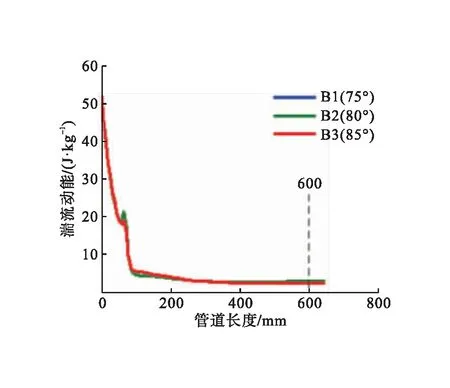
a)管道轴线
由于近壁层是管壁附着污垢清洗作业的有效区域,故在初始条件相同的前提下,近壁层的流速和湍流动能越大,清管效果越好,因此确定射流清管器环状喷嘴的最优外锥角为80°。
3 结论
1)射流清管器环状喷嘴环状射流与轴心射流交互,对整个管壁进行均匀吹扫,并将管壁附着的粉尘、固体杂质等污垢卷入射流流场,从而减小清管器运行阻力,可有效预防清管器前端污垢柱的形成,显著降低清管频率与卡堵风险。
2)由于环状射流与轴心射流的相互扰动,环状喷嘴内锥角和外锥角的变化只影响管内射流吹扫速度、湍流动能大小及管道径向吹扫效果,不影响管道的轴向吹扫范围。
3)通过对不同锥角的射流流场进行数值模拟,以射流流速和湍流动能作为吹扫效果评价指标,则环状喷嘴内锥角为90°、外锥角为80°时能达到最佳的管道内壁吹扫效果。

