高压直流电场作用下的甲烷-氧气层流扩散火焰稳定性

吴心祎， 吴婧瑄， 龚 岩， 于广锁,2

（1.华东理工大学洁净煤技术研究所, 上海 200237；2.宁夏大学省部共建煤炭高效利用与绿色化工国家重点实验室, 银川 750031）

煤炭是我国的基础能源和战略原料，煤炭的清洁高效利用是社会经济发展和生态文明建设的客观要求，也是保障国家能源安全的现实需要[1-2]。气流床煤气化是煤炭清洁高效利用的核心技术，是煤基大宗化学品合成、煤制液体燃料、煤制天然气和制氢等过程工业的龙头技术和关键技术[3]。在大型水煤浆气化技术发展过程中，仍存在一些亟待解决的瓶颈问题，如耐火砖在其服役过程中受到高温火焰等的剧烈冲刷和侵蚀，造成了炉内耐火衬里的失效，这直接导致气化炉运行周期缩短、生产成本增加，极大地影响了超大型气化装置长周期、高效、稳定运行。高温火焰侵蚀是导致耐火砖损毁的重要原因，耐火衬里使用寿命的提高主要依靠高性能耐火材料的开发和炉膛结构的优化，现阶段新型耐火材料的研制还未实现大规模突破，而通过优化耐火衬里结构以延长其寿命的效果有限，耐火衬里失效仍是气化技术面临的共性难题[4]。不同炉型的蚀损和失效的区域亦有所区别，不同气化技术的蚀损问题解决方法不具备普适性[5]。因此，亟待开发一种灵活且通用的火焰动态调控方式，从而有效降低高温火焰对耐火衬里的侵蚀，保障气化炉长周期、高效、稳定运行。

火焰作为弱电离等离子体，其电特性会受到电场的影响。自上世纪起，国内外诸多学者开展了电场对火焰的影响研究。Calcote 等[6]通过实验发现电场会影响火焰的稳定性。火焰内带电离子受到电场作用后，快速移动的离子会对载气产生阻力而导致气体流动，即产生离子风效应。Weinberg 等[7]从离子风效应和带电离子运输效应的定量关系出发，指出离子风效应产生的实际效果取决于当前的电流密度。文献[8]发现，电子温度对电场也有较强的敏感度，当施加电场时，电场不仅会加快电子搅动速度，也会抑制电子附着，进而改变电子温度，反应速率随着电子温度的升高而加快。

火焰中的离子和电子是由于化学电离产生的，在燃烧过程中会产生CHO+、H3O+等正离子，其数量大约每毫升在109～1012个，层流扩散火焰的阻值也非常大，通常在108Ω 量级[9-10]。从微观角度而言，电场会诱导火焰中正离子和中性粒子向负极运动，当火焰中正离子和中性粒子发生碰撞时，正离子会优先加速向负极运动，它的部分动量转移到中性粒子上，从而产生体积力和离子风，使得火焰外观变化[11-12]。离子风效应被认为是直流电场影响火焰燃烧过程的主要机理，其实质就是电场所引起的离子定向移动。文献[13]认为离子风效应还与外加电场强度以及火焰在电场中驻留的时间相关。

Lewis 等[14]通过实验发现消除正离子会导致火焰的熄灭，证明了正离子在维持火焰稳定性中起到了关键作用。文献[15-16]验证了电场对预混火焰及非预混射流火焰稳定性的影响。文献[17]基于离子风效应，研究了直流电场对层流非预混乙烯火焰的作用，发现在正电压下可以观察到不稳定的波动火焰，此现象也是由于正离子受到了洛仑兹力的作用。Belhi 等[18]对电场作用下火焰的稳定性进行了数值模拟研究，发现离子风可以促进火焰的稳定性。

不同的电极形状由于其表面曲率不同也会对火焰外观产生不同的效果[19]。Boom 等[20]通过实验发现电场引起的燃烧速度变化会随外加电压呈非线性增长，且受电极间距的影响。同样地，电场也会改变火焰的传播速度[14,21]。唐安东等[22]在定容燃烧器中研究了非均匀电场对火焰传播速度的影响，发现火焰的传播速度随着施加电场强度的增加而增加；且正负电场都会增强火焰的稳定性，而负电场的效应更显著[23]。在点电极下施加负电场也会使火焰的传播速度加快，且随着电压增加而增加[24]。段浩等[25]进一步比较了不同电极形状对火焰传播速度的影响，发现网状电极对火焰传播的促进作用最为显著，柱状电极次之，点电极最弱，与各形状电极产生的电场强度一致。Sayed-Kassem 等[26]所建立的模型在电场条件下能定性地再现火焰实际的燃烧情况，数值模拟结果表明电场可以改变火焰形状、促进燃烧、提高离子的产生。

由于炉膛内火焰过于复杂，且电场对火焰稳定性的定量研究并不完善，故本研究以甲烷-氧气扩散火焰为切入点，通过对甲烷-氧气火焰施加不同强度的直流高压电场，即通过改变所施加直流电压的大小及电极间距，观察火焰脉动受电场的影响，探讨直流电场火焰稳定性的可能性。与传统方法不同，本研究并非通过调整气化炉喷嘴参数以达到稳定燃烧的目的，而是通过直流高压电场这种通用灵活、可实时操控的技术调控非预混扩散火焰，从而提高火焰稳定性，降低由于火焰脉动而产生的燃烧不稳定性。本文为降低气化炉内火焰对耐火砖壁面的侵蚀提供了理论依据和实践参考。

1 实验系统及方法

本实验系统采用双通道非预混喷嘴，喷嘴配备一路燃料管道以及一路氧气管道（图1）。实验采用甲烷作为燃料，甲烷自气罐通过质量流量计控制流量后，由燃料管道输送至喷嘴中心通道，氧气自氧气气罐通过质量流量计进入喷嘴外通道。喷嘴外部包裹气体分布器，氩气通过气体分布器被均匀分散以隔绝喷嘴火焰与空气气氛。可调直流高压电源在喷嘴和环形石墨电极之间施加单向电场，直流电源负极通过高压电缆与铂-铑合金连接于环形石墨电极，并置于火焰上方的线圈内，电源正极通过高压电缆直接连接于喷嘴下方。喷嘴与支架和管路之间、石墨电极与环形支架之间均采用耐高压绝缘连接。可调电源与工作站相连，通过数控软件在线调控电源电压。采用高速摄像仪（Pco.dimax S4）拍摄火焰图像，其最大分辨率为2016×2016 pixel，最高帧率（f）为1 279 fps，数据经工作站储存和分析。其中，可调直流高压电源的电压调节范围为800～10 000 V，设置高速摄像仪的帧率f= 250 fps，拍摄时长t= 2 s。本实验中的层流扩散火焰参数如表1 所示。对于同轴射流火焰而言，雷诺数是判断其燃烧形态的重要依据。通常，层流扩散火焰向湍流扩散火焰过度的临界雷诺数（Rec）为2 000～10 000[27]，经计算，本研究中的火焰雷诺数均小于1 000，属于层流扩散火焰。

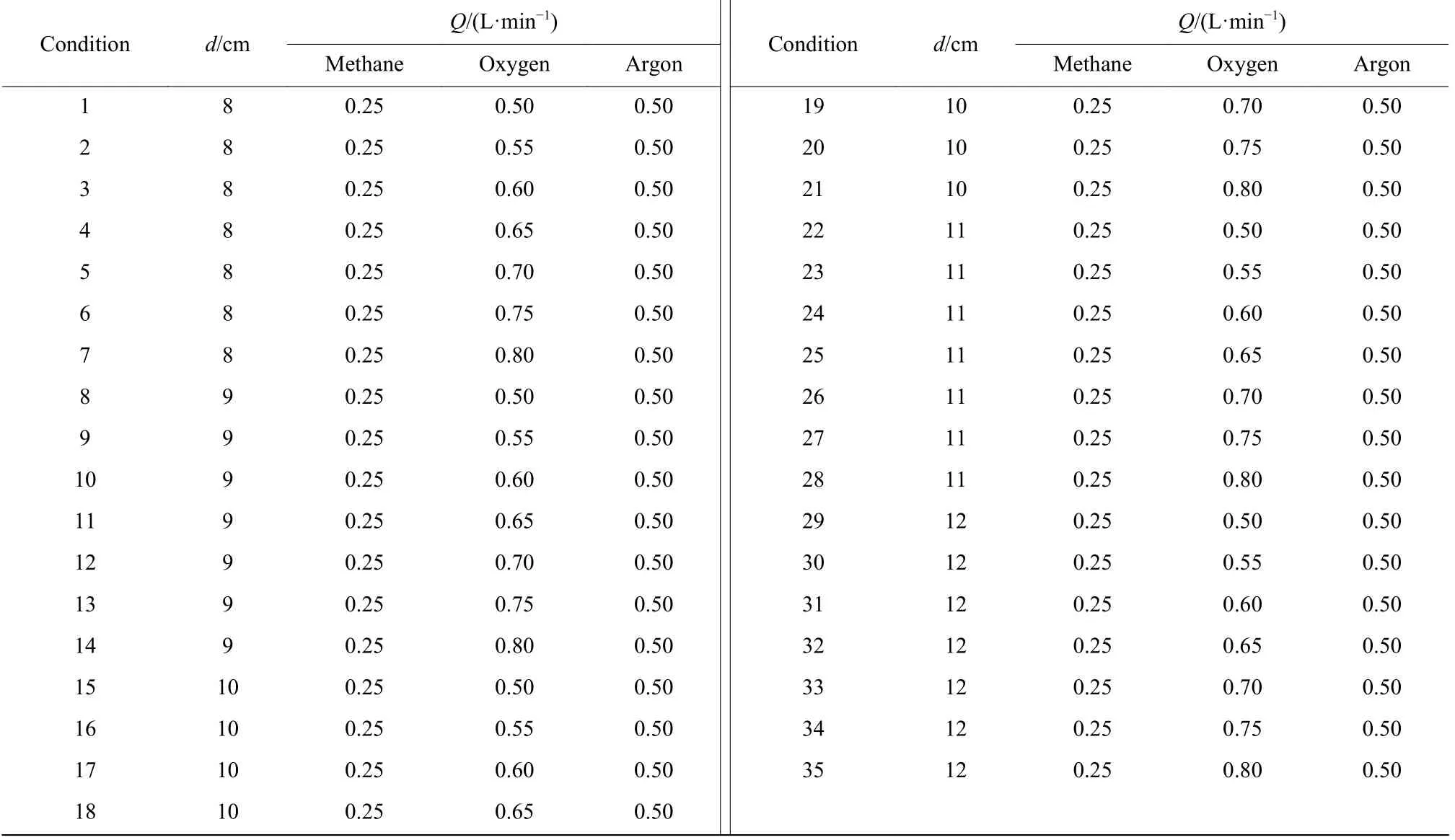
表1 电场对扩散火焰的实验条件Table 1 Experimental conditions of electric field on diffusion flame

图1 在电场作用下的层流火焰实验平台Fig.1 Laminar flame experimental platform under electric field

2 电场对火焰稳定性的影响

对于层流扩散火焰而言，其火焰长度与初始速度及管径均无关，只和初始体积流量（Q）有关[28]。实验研究了固定电极间距（d）下直流电场对甲烷-氧气层流射流火焰振荡情况的影响。对于甲烷流量（QCH4）、氧气流量（QO2）分别为0.25、0.50 L/min 的非预混甲烷-氧气火焰，当量比（λ）即为1.0。当量比的具体定义为：氧气和甲烷实际的物质的量之比与氧气和甲烷完全燃烧时物质的量之比的比值。若λ＜1.0，则为不完全燃烧。在未施加直流电压时，火焰会出现显著的振荡情况。为进一步用数值直观表征火焰振荡情况，对高速摄像仪所拍摄的火焰图像进行归一化处理，首先将所拍摄的火焰图片进行裁剪。为更好地展现火焰全貌，通过Image J 图像处理软件将火焰图像裁剪为分辨率270×90 pixel 的图像。随后将拍摄所得图像简化，通过图像处理软件将图像中的各个像素点的亮度进行归一化处理。为更好体现火焰变化，选取212的灰阶度，将火焰图像转化为其灰阶度的矩阵，随后对矩阵中的各行进行均值处理。如图2 所示，对于λ=1.0 的非预混甲烷-氧气火焰，当其未施加电场时会出现显著的振荡现象。

图2 未施加电场时火焰的高度变化Fig.2 Flame height change without electric field

在高速相机所拍摄的500 张火焰形态图经数值化处理后，其同一高度下归一化均值的变化情况如图3 所示。非预混甲烷-氧气火焰在未施加电场时呈现较为规律的振荡，且火焰振荡的幅度随λ的增加先上升，直至当λ=1.3 时，再逐渐减小，并趋于稳定，如图4 所示。

图4 火焰振荡幅度随λ 的变化趋势Fig.4 Variation trend of flame pulsation amplitude with λ

电场强度是电场的特征参数。对于匀强电场而言，固定两点的电场强度与两端的电压及两点的间距有关；对于环形电极而言，其轴向电场强度与电压及轴向距离有关；这两种情况（匀强电场和环形电极）的电场强度均随间距的增加而减小。本实验中由于高压电场的电场强度无法直接测量，火焰内部场强较为复杂，无法直接通过计算获得，故本文从电压及电极间距两个变量出发，探讨电场对于火焰稳定性的影响。

2.1 电压对火焰稳定性影响

当d=8 cm、施加不同电压时，QCH4= 0.25 L/min、QO2= 0.50 L/min、λ=1.0 条件下非预混甲烷-氧气火焰的振荡情况如图5 所示。火焰的振荡情况随着电压的增加逐渐趋于平缓，当电压达到3.1 kV 时，火焰的振荡几乎停滞（图5（d））。继续提高所施加的电压至4.0 kV时，火焰依旧维持稳定状态（图5（f））。

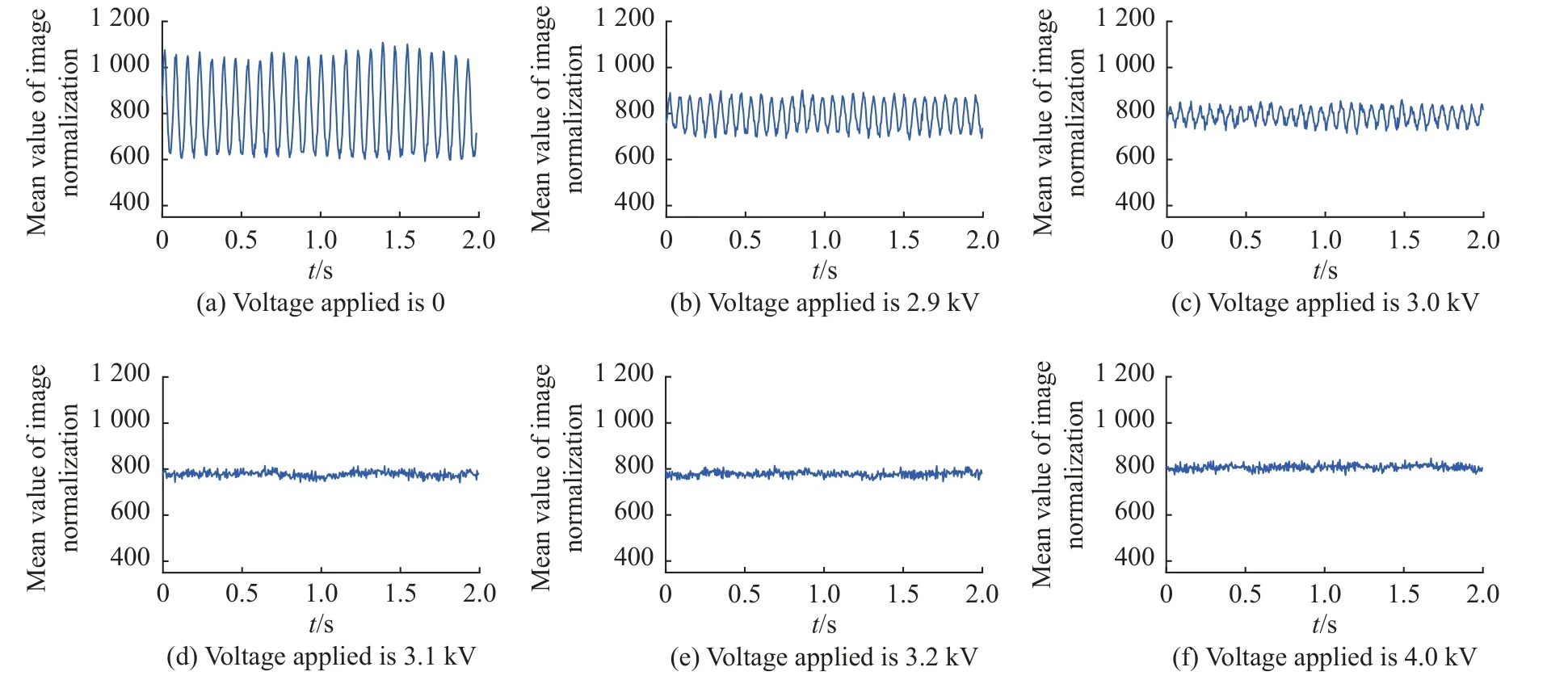
图5 火焰振荡情况与直流电压的关系Fig.5 Relationship between flame pulsation and direct current voltage

火焰振荡能谱图与直流电压的关系更清晰地反映出火焰由振荡归于平稳的变化情况，如图6 所示。经过傅里叶变换后，能谱图中的峰值代表火焰的振荡程度，峰值越大，表明火焰振荡越剧烈；峰值所对应的频率值代表了火焰振荡的频率。当火焰尚不稳定、存在振荡时，如图6(a)、6(b)和6(c)所示，在频率为10～20 Hz 的范围内，存在一个特征峰。当电压达到3.1 kV 时，火焰趋于稳定，其对应的能谱图中亦无特征峰，各工况的峰值出现在频率趋于零的位置，如图6(e)、6(f)和6(g)所示。故对于d= 8 cm、QCH4=0.25 L/min、QO2= 0.50 L/min的非预混层流甲烷-氧气火焰而言，当直流电压达到3.1 kV 时，其燃烧趋于稳定，后文将此电压值简称为稳定电压。

图6 火焰振荡能谱图与直流电压的关系Fig.6 Relationship between flame pulsation energy spectrum and direct current voltage ( QCH4 = 0.25 L/min, QO2 = 0.50 L/min、λ=1.0)

2.2 电极间距对火焰稳定性的影响

对于不同气体混合比的甲烷-氧气火焰，其稳定电压也各不相同，且对于施加在火焰上、下端的直流电场而言，电极间距也是较为重要的影响因素之一，因为电极间距会改变施加于火焰上的电场强度。当电极间距分别为8、9、10、11、12 cm 时，对不同气体混合比下甲烷-氧气火焰的稳定电压进行测量。固定甲烷流量为0.25 L/min，通过改变氧气流量来控制火焰燃烧的当量比。测量结果如图7 所示。

图7 不同电极间距下火焰稳定电压随λ 的变化Fig.7 Variation of flame stable voltage with λ at different electrode spacing

由图7 可以看出，火焰的稳定电压会受到电极间距的影响。当电极间距差别较小时，其对火焰稳定电压的影响并不显著；但将电极间距8 cm 和12 cm下不同当量比火焰所对应的稳定电压进行比较，可以发现，对于相同当量比的火焰，电极间距越大，所需的稳定电压就越高。同时，无论电极间距的大小如何变化，对于固定电极间距下的非预混甲烷-氧气火焰，其稳定电压随当量比的变化趋势是一致的，即稳定电压先随当量比的增加而增加，直至当量比达到1.2～1.3 时，稳定电压达到峰值；随后，稳定电压会随着当量比的增加呈下降趋势。其整体趋势与图4所示的未施加电压时，火焰振荡幅度随当量比的变化规律基本一致。

上述结果表明，当对非预混火焰施加正向直流电场（即电流方向与燃料射流方向一致）时，可以增强火焰的稳定性，推断其原因是由于正向电场使得火焰内正离子定向运动，产生离子风效应，填补了由于燃料及氧气密度不同所产生的漩涡结构，故火焰的振荡现象逐渐减弱直至消失。当电极间距不同，当量比为1.0～1.3 时，甲烷-氧气非预混层流火焰的稳定电压随初始振幅的增长单调递增，如图8 所示。将图8 结果进行线性拟合，拟合直线的残差平方和（SSE）均小于0.040 00；只有当电极间距为8 cm 时，其稳定电压随初始振幅变化的拟合直线的相关系数R2＞0.990 00，而其余电极间距下，稳定电压随初始振幅的增长均无法满足线性关系。

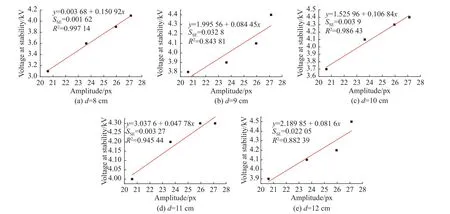
图8 不同电极间距下初始振幅与稳定电压的关系（λ=1.0～1.3）Fig.8 Relationship between initial amplitude and stable voltage at different electrode spacing (λ=1.0～1.3)

3 结 论

（1）高压直流电场可以增强脉动层流火焰的稳定性，在对火焰施加与射流方向一致的高压直流电场，且电极间距不变的情况下，电压越高，电场强度越高，其增强火焰稳定性的效果越强。对于当量比为1.0～1.3 的甲烷-氧气非预混层流火焰，稳定电压与火焰初始脉动振幅（当量比）呈单调递增的关系，初始振幅（当量比）越大，火焰所需的稳定电压就越高。稳定电压通常在火焰当量比为1.3 时达到峰值，随后火焰的初始振幅随当量比的增加而减小，稳定电压也随着初始振幅单调递减。

（2）电极间距对电场稳定火焰的能力产生一定影响，但其影响较小，只有当电极间距相差较大时才有明显差异。对于电极间距为8 cm 及12 cm 的甲烷-氧气非预混层流火焰，电极间距越大，为保证火焰受到同样的电场强度，稳定相同振荡幅度的火焰（即同一当量比下的火焰）所需的直流电压值就越高。

（3）电场强度越大，直流电场对火焰的稳定效果越好；电场强度越低，直流电场对火焰稳定性的影响越小。