Towards robust neural networks via a global and monotonically decreasing robustness training strategy∗

Zhen LIANG ,Taoran WU ,Wanwei LIU‡ ,Bai XUE ,Wenjing YANG,Ji WANG,Zhengbin PANG

1Institute for Quantum Information & State Key Laboratory of High Performance Computing,National University of Defense Technology,Changsha 410073,China

2State Key Laboratory of Computer Science Institute of Software,Chinese Academy of Sciences,Beijing 100190,China

3School of Computer Science and Technology,University of Chinese Academy of Sciences,Beijing 100190,China

4College of Computer Science and Technology,National University of Defense Technology,Changsha 410073,China

5Key Laboratory of Software Engineering for Complex Systems,National University of Defense Technology,Changsha 410073,China

Abstract: Robustness of deep neural networks (DNNs) has caused great concerns in the academic and industrial communities,especially in safety-critical domains.Instead of verifying whether the robustness property holds or not in certain neural networks,this paper focuses on training robust neural networks with respect to given perturbations.State-of-the-art training methods,interval bound propagation (IBP) and CROWN-IBP,perform well with respect to small perturbations,but their performance declines significantly in large perturbation cases,which is termed “drawdown risk” in this paper.Specifically,drawdown risk refers to the phenomenon that IBPfamily training methods cannot provide expected robust neural networks in larger perturbation cases,as in smaller perturbation cases.To alleviate the unexpected drawdown risk,we propose a global and monotonically decreasing robustness training strategy that takes multiple perturbations into account during each training epoch (global robustness training),and the corresponding robustness losses are combined with monotonically decreasing weights(monotonically decreasing robustness training).With experimental demonstrations,our presented strategy maintains performance on small perturbations and the drawdown risk on large perturbations is alleviated to a great extent.It is also noteworthy that our training method achieves higher model accuracy than the original training methods,which means that our presented training strategy gives more balanced consideration to robustness and accuracy.

Key words: Robust neural networks;Training method;Drawdown risk;Global robustness training;Monotonically decreasing robustness

1 Introduction

In recent years,artificial intelligence (AI) and deep learning (DL) have witnessed enormous success in various domains,such as image recognition(Chen and He,2021;Tian et al.,2021),natural language processing(Devlin et al.,2018),and automatic driving (Bojarski et al.,2016).Behind these great achievements,deep neural networks (DNNs) have become dominant computing models and have made significant contributions to the prosperity of AI and DL.Nevertheless,DNN behaviors are far from infallible;e.g.,imposing human-imperceptible perturbations on the input samples causes drastic changes in the outputs (Goodfellow et al.,2015).The unexpected outputs would result in loss of life and property (Ma et al.,2018),especially in safety-critical applications.

Consequently,there is a pressing need to guarantee that the behaviors of DNNs obey some given properties before their deployments in practice,like safety (Wang et al.,2018a),robustness (Katz et al.,2017),reachability (Tran et al.,2019),and fairness(Sun et al.,2021).Among them,robustness,which refers to DNNs working stably under minor input disturbances,is one of the most important properties in academic and industrial communities.On one hand,researchers focus on proposing dozens of robustness verification approaches on different kinds of DNNs(Weng et al.,2018b;Zhang H et al.,2018;Balunović et al.,2019;Ko et al.,2019;Liu WW et al.,2020;Du et al.,2021;Guo et al.,2021;Liu JX et al.,2022;Zhang YD et al.,2022;Zhao et al.,2022),with the techniques used ranging from abstract interpretation(Ryou et al.,2021)and mixed integer linear programming (Tjeng et al.,2019) to symbolic execution (Li et al.,2019).On the other hand,besides verifying the robustness of certain trained DNNs,researchers pay attention to training robust neural networks (NNs)against certain perturbations.Compared with providing post facto conclusions indicating whether the robustness holds or not,providing guaranteed robust NNs with proper training methods seems to be more important,in the sense of NN applications and deployments.

There have been extensive studies concentrating on training robust NNs so far.One natural robust training method is data augmentation (Goodfellow et al.,2015),which generates training data by sampling randomly in the perturbation-specified input region.The original augmentation idea is inefficient and is developed by attack algorithms,like the fast gradient sign method (FGSM) (Goodfellow et al.,2015) and projected gradient descent (PGD)method (Madry et al.,2018),to improve the effectiveness and efficiency of sampling.Furthermore,in some recent literature,researchers attempted to train DNNs with verifiable guarantees on robustness performance,such as linear relaxation (Dvijotham et al.,2018;Mirman et al.,2018;Wang et al.,2018b;Zhang H et al.,2020),interval bound propagation(IBP) (Gowal et al.,2018;Mirman et al.,2018),ReLU stability regularization based method (Xiao et al.,2019),and global robustness based method(Leino et al.,2021).Among these methods,IBP(Gowal et al.,2018)is a simple and efficient method for training verifiable robust DNNs.To refine the loose bound estimation of IBP,CROWN-IBP(Zhang H et al.,2020) combines IBP with tighter linear relaxation work (Zhang H et al.,2018) and reaches state-of-the-art performance,easing the instability of the training procedures and sensitivity to hyperparameters simultaneously.Additionally,we refer interested readers to Liang et al.(2023) for a comprehensive review.

In this work,instead of seeking a completely novel robust NN training method,we turn our attention to alleviating the great challenge that existing IBP-family training methods encounter;i.e.,IBP and CROWN-IBP methods are likely to fail under large input perturbations.This phenomenon is called “drawdown risk” in this paper.Therefore,IBP-family training methods cannot provide the expected robust NNs in large perturbation cases.After analyzing the training paradigm of IBP and CROWN-IBP,we give a possible explanation for the drawdown risk.It is likely to stem from training robust DNNs toward a single perturbation value each time(training epoch),and thus locality leads to failure,with large perturbations in particular.Therefore,our global robustness strategy takes multiple certain perturbations (sub-perturbations) into account in the training phases,in place of a single perturbation.In addition to training DNNs with those sub-perturbations globally,our remedy for existing IBP-based training methods investigates the monotonically decreasing combination weights of the robustness optimization corresponding to different perturbations,termed the monotonically decreasing robustness training strategy.The so-called monotonically decreasing robustness training strategy requires that the smaller a sub-perturbation is,the more weight it should be assigned during the DNN training phases.Moreover,our proposed global and monotonically decreasing robustness training strategy works for any existing training method and is simple to implement.

The contributions of this paper are as follows:

1.We observe and formalize the drawdown risk problem existing in the IBP and CROWN-IBP training methods,and explore a possible reason that IBPfamily methods fail under large perturbation cases,that is,the drawdown risk resulting from local robustness training (LRT).To overcome this hazard,we propose the idea of global robustness training(GRT),considering some certain perturbations together,instead of only a single perturbation value,during the training processes.

2.Taking multiple perturbation values into account,we seek a monotonically decreasing weight strategy for combining them during the training phases and form the new loss function.Under the guidance of the monotonically decreasing weight strategy,the remedy training method is compatible with existing IBP-based training methods and can be treated as a generalization of them.

3.We implement our training strategy on the state-of-the-art work,CROWN-IBP.The experimental results illustrate that our strategy keeps (or improves a little) the performance in existing small perturbation cases and enhances the performance significantly in large perturbation cases,alleviating the drawdown risk during training.

2 Background and related works

AnL-layer (classification) DNNNcan be defined recursively as follows:

whereh(0)(x)=x(i.e.,the input),andnlis the number of neurons located in thelthlayer,also called the layer dimension.n0refers to the input dimension of neural networkNandnLrepresents the number of prediction classes,i.e.,the output dimension.Wlandblare the weight matrix and the bias in the adjacent (l-1)thandlthlayers,respectively.σis the nonlinear element-wise activation function,and we usezto represent pre-activation neuron values andhfor post-activation neuron values.

2.1 Robustness of DNNs

Robustness is one of the most important properties of DNNs,and there are some definitions of NN robustness with minor differences (Casadio et al.,2022),like classification robustness,standard robustness,and Lipchitz robustness.In this work,we focus on the widely used classification based definition,which implies that all samples within a given range have the same prediction class:

Definition 1(Classification robustness) A DNNNis∊-robust with respect to input examplexwith ground truth labely,if

where the arg max(·) function obtains the classification label corresponding to input ˜xfrom the network outputy=N(·) and∊is called the perturbation radius (or perturbation for short).

In contrast,for a given range of inputs,standard robustness implies that the resulting outputs should vary within a tolerable range,and Lipchitz robustness requires that the range of output variations be proportional to the range of input variations.To formally reason about classification robustness,an important quantity,the robustness margin,is derived through robustness specification in the sense of Definition 1.

Definition 2(Robustness specification matrix and robustness margin) An∊-robustness with respect to examplexwith ground truth labelyis essentially associated with a specification matrixC ∈RnL×nL,which gives a linear combination for NN output:

More importantly,each element in the vectorm:=CN(x)actually computes the robustness margin between the ground truth labelyand other labels,i.e.,the difference value between the prediction probability of the truth label and the prediction probability of other labels,denoted bym(x,∊).Moreover,the robustness margin plays an important role in NN verification related work.

Combining Definitions 1 and 2,we propose the following theorem to indicate the satisfiability of the robustness of NNs.The proof is obvious according to Definitions 1 and 2.

Theorem 1The robustness with respect to a neural networkN,an input examplex,and a perturbation radius∊holds if and only ifm(x,∊)=CN(x)＞0 (here＞is an element-wise operator).

To be more specific,let us assume that an example neural networkNis designed to predict a label among five classes(i.e.,five output neurons),and that the ground truth label of the inputxis the third class.Then,according to Eq.(4),the specification matrixCis constructed as follows:

Further,suppose that the outputs of two different examplesandare

respectively (the outputs are processed by the softmax activation function,causing the sum to be 1),where,∈{|||-x||∞ ≤∊}.Next,the computation results with respect to the specification matrix and outputs indicate whether the robustness holds or not.That is to say,because

Nis robust in exampleand it is not robust with respect to exampledue to

Consequently,the robustness ofNwith respect to (w.r.t.) the samplexand∊is falsified according to Theorem 1,because we find an input sample that does not satisfym(x,∊)＞0.Such examples are called“adversarial examples” in the literature.

2.2 Robustness verification of DNNs

Resorting to the nice feature of robustness margin,various methods have been developed estimatingm(x,∊)to verify the∊-robustness with respect to examplex.If the estimated lower bound(x,∊)＞0,then networkNis verifiably robust for anyℓ-norm perturbation less than∊on examplex,as(x,∊)≤m(x,∊).Moreover,it has been found that computing the exact output ranges or margins of DNNs is nonconvex and NP-complete (Katz et al.,2017;Weng et al.,2018b).In what follows,we useandto represent the estimated upper bound and lower bound of∗,respectively.In this paper,our main focus is on the training methods of the IBP family,and we primarily introduce the estimation techniques form(x,∊)using IBP and CROWN-IBP.

IBP: IBP adopts a simple and efficient bound propagation rule for margin estimation,which can be formulated in Eq.(10),where|W(l)|takes the element-wise absolute value and=x+∊,=x-∊according to the interval arithmetic and perturbation definition.Thus,the robustness margin can be computed with the specification matrixCdefined in Eq.(4).Specifically,the upper and lower bounds of the output neurons are obtained from Eq.(10) via layer-by-layer propagation,and then the bounds ofm(x,∊) are computed with the specification matrixC,particularly the lower bound(x,∊).Note that the activation functions are required to be monotonically increasing to ensure the computation correctness of Eq.(10),while it is not a strict condition and common activation functions meet this requirement,such as Tanh and Sigmoid.

To sum up,IBP is computationally efficient,which is the dominant reason why it is popular in estimating the robustness margin.However,IBP provides very loose estimation bounds,and thus in most cases DNN robustness is unverifiable.

CROWN: To obtain tighter estimation bounds,CROWN uses linear relaxations on the non-linear activation function ReLU to estimate the range bounds of DNNs.On the top ofcomputed by Eq.(10),CROWN first selects the stable neurons,including always activeand always inactiveneurons.Then for the other unstable neurons,CROWN shows a linear relaxation for ReLU activation:

where 0≤αk ≤1.To minimize the relaxation error further,CROWN proposes to selectαk=1 whenand 0 otherwise.Combining the stable and unstable neuron cases,the ReLU function can be effectively replaced with a linear layer,estimating the upper and lower bounds of the output with

whereare the diagonal weight matrices corresponding to the lower and upper cases of the relaxed ReLU respectively.Furthermore,considering the affine part (i.e.,Wx+b) and ReLU function,the output of theithneuron is bounded by linear hyperplanes:

The estimation is also carried out layer by layer,as in IBP.Similar work based on linear relaxations was conducted in DeepZ (Singh et al.,2018),Deep-Poly (Singh et al.,2019),and Fast-Lin(Weng et al.,2018b),and we refer readers to Salman et al.(2019)for a comprehensive review.

CROWN-IBP: Just as its name implies,CROWN-IBP combines IBP and CROWN;i.e.,it takes a linear combination of the estimated lower bounds from IBP and CROWN as the final estimation results.

These notations are used and retain the same meanings throughout this paper.

3 Methodology

During DNN training procedures,loss functions are used to quantify the difference between DNN predictions and the ground truth label and optimize the network parameters further (Duda et al.,2001;Murphy,2012).In nominal training processes,without considering robustness,cross-entropy losses are generally adopted,evaluating the difference between output probability distributionN(x)and real distributiony(such as a one-hot vector):

wherePdenotes the number of prediction classes andθrepresents the network parameter set.The smaller the cross-entropy,the more accurate the output,and we label the loss function with acc.

3.1 Issue: locality leads to drawdown risk

In the literature on training robust DNNs,generally the evaluation of robustness has been considered together with the performance of NNs.According to Theorem 1,(x,∊) can indicate the satisfiability of NN robustness(m(x,∊)(x,∊)＞0),and thus the new loss function is formed consequently:

where Lossrobis the loss term evaluating DNN robustness,andκ(0＜κ ＜1) is the hyperparameter that balances DNN accuracy and robustness.

Gowal et al.(2018) used IBP to estimatem(x,∊),forming the following loss function:

With the estimation bound,IBP achieves outstanding performance,even though the bounds are relatively loose.

CROWN-IBP (Zhang H et al.,2020) combines IBP and CROWN to bound the robustness margins with forward (IBP-style) and backward (CROWNstyle)estimations.With the lower bounds of robustness margins,we have

whereβ(0＜β ＜1) is a hyperparameter that balances the IBP estimation bound and CROWN estimation bound.CROWN-IBP obtains state-ofthe-art performance by tightening the estimation bounds.

However,applying these methods to large perturbation cases tends to fail and cannot provide faithful and robust DNNs.In Fig.1,we show the evaluated verified errors trained with representative robust DNN training methods IBP and CROWNIBP against different perturbations.The verified error is the percentage of test samples where at least one element inm(x,∊) is less than 0.It is a guaranteed upper bound of the test error under anyℓ∞perturbation (Zhang H et al.,2020).The verified errors are the indications of network robustness,and the larger the errors,the worse the robustness.The verified error varies significantly depending on the verification techniques used.To ensure fair comparisons,we calculate the verified error using a complete verification algorithm(Tjeng et al.,2019)and an exact solver Gurobi,as in Gowal et al.(2018).In Tjeng et al.(2019),the verification problem was formulated as a mixed integer programming (MIP) problem to be solved by Gurobi within a given time limit.If the solver times out,the verification problem is reformulated as a linear programming (LP) problem(Ehlers,2017) and solved by Gurobi again.If neither approach can provide a solution within the given time limit,we consider the example to be attachable.The calculation method is also used in Section 4.

It can be observed that the verified errors w.r.t.0.01 evaluated on the models trained by IBP and CROWN-IBP are both below 5% in the perturbation 0.2 and 0.4 cases.The verified errors w.r.t.the final perturbations(i.e.,0.2 and 0.4)are still acceptable,whereas for perturbation 0.5,the verified errors on 0.01 are much larger and they increase obviously,for both IBP and CROWN-IBP training methods.In summary,the verified error remains relatively low in the small perturbation cases,while it drastically increases in the large perturbation ones,which is termed the drawdown risk of performance.This means that the existing IBP-family training methods perform poorly on large perturbations,which is the key issue concerned and addressed in this paper.

Focusing on Eqs.(15)-(17),in each training epoch,the optimization renders the parameter updating robust with respect to a single perturbation value (i.e.,the given∊).We name this training style “local robustness training” (LRT for short) afterward.Even though “warm-up” (training without Lossrob)and“ramp-up” (increasing the perturbation value to the specified one gradually)processes are introduced in the practical implementation,LRT still exists in each training epoch.It continues to train NNs on the basis of the previous training,while the previous training effect becomes weaker and weaker as the training progresses,because only one perturbation value is considered each time.Consequently,locality can be regarded as a reasonable explanation for the drawdown risk.

3.2 Global robustness training strategy

To alleviate the drawdown risk of LRT,as shown in Fig.2a,in this paper,we propose a novel training strategy,GRT.Ideally,the GRT strategy refers to training with the sub-perturbation range 0＜∊train≤∊simultaneously,instead of a single perturbation∊.Then the robustness loss is formulated as

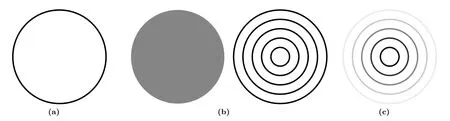
Fig.2 Demonstration of the global and monotonically decreasing robustness training strategy versus local robust training (LRT): (a) LRT;(b) global robustness training (GRT) strategy (left is the ideal case and right is the practical case);(c) monotonically decreasing robustness training strategy

Essentially,Eq.(18) is an ideal presentation,and in practice it can be relaxed and approximated as follows: whereNis the number of different sub-perturbations and is termed the robustness size.It can be seen that the GRT strategy degenerates into LRT whenNtakes 1.

With the GRT strategy,we would like to consider multiple perturbation values (subperturbations)during the training phase to avoid the aforementioned locality training.Moreover,when the robustness size is determined,we adopt a uniform sampling strategy to select sub-perturbations during the training phase,as shown in Eq.(19).The comparison of LRT and GRT styles is shown in Fig.2,along with the ideal and practical cases in Fig.2b,where circles in different radii represent different sub-perturbations.

3.3 Monotonically decreasing robustness training strategy

In addition to the GRT strategy,which takes multiple sub-perturbations into account in each training epoch,we propose a monotonically decreasing robustness training strategy that combines different robustness loss values corresponding to each sub-perturbation.In Eqs.(18) and (19),the GRT strategy takes the average value of all the losses by default and this undifferentiated combination of the losses is not sufficient,as illustrated in Section 4.

To organize the different loss values,a monotonically decreasing robustness training strategy makes sense.It means that the smaller a sub-perturbation is,the more weight its loss value deserves.Therefore,the robustness loss function becomes

whereciis the robustness weight.The reasons for adopting the monotonically decreasing robustness training strategy are mainly threefold:

1.From the view of robustness itself,the robustness with respect to smaller perturbations is more important than that of larger ones.That is to say,the smallest perturbation that a DNN can defend is a significant metric for evaluating its robustness.Additionally,in the domain of robustness verification,methods attempt to seek out the minimum perturbation as the robustness radius for the guidance of related applications.

2.From the view of training feasibility,it is more difficult for methods to train robust DNNs against larger perturbations compared to smaller ones.Therefore,during the robust training,more attention should be paid to the relatively feasible objectives and less to the hard ones.However,even with smaller weights,we do not give up optimizing the robustness against larger perturbations.

3.From the view of the relationship among the robustness strategies on different sub-perturbations,a DNN is more likely to be robust on larger perturbations if it is more robust with respect to smaller ones.This means that the efforts to improve the robustness against smaller perturbations during the training procedure also contribute to robustness in larger perturbation cases.

The monotonically decreasing robustness training strategy on the GRT style is demonstrated in Fig.2c,where the darker the color,the more importance is assigned to the sub-perturbation.Moreover,considering the limit case of the perturbation approaching zero,our proposed monotonically decreasing robustness training strategy causes the robust training to degenerate into nominal training,and it is absolutely correct to improve the accuracy metric in the case without perturbation.

4 Experiments

In this section,we describe how we implement our proposed training strategy on top of the representative and state-of-the-art work,CROWNIBP,which we term GM-CROWN-IBP (global and monotonically decreasing CROWN-IBP).We use the PyTorch implementation version of CROWNIBP (https://github.com/huanzhang12/CROWNIBP).We evaluate GM-CROWN-IBP on the MNIST and CIFAR datasets with three network models used in CROWN-IBP(Zhang H et al.,2020),whose architectures are displayed in Table 1,and we refer readers to Gowal et al.(2018) for details.Herein,we follow their previously used notations,i.e.,DM-small,DMmedium,and DM-large.All the experiments are carried out in the same platform,which includes 32 Intel Xeon Gold 6254 cores with 3.10 GHz frequency.The operating system is Ubuntu 18.04.3,and we list the detailed hyperparameters in the Appendix for reproducing the experimental results.

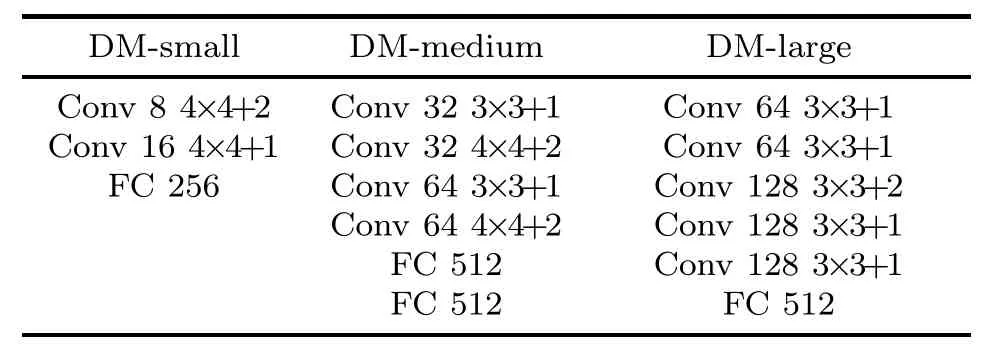
Table 1 Neural network architectures

We compare GM-CROWN-IBP with IBP and CROWN-IBP in terms of the standard error and verified error,together with the best errors reported in the literature.The standard (clean) error refers to the proportion of classification errors,and recall that the verified error represents the percentage of test examples that violate robustness;they are used to evaluate the accuracy and robustness of models separately.Moreover,the verified error is a guaranteed upper bound of the test error under perturbations with any attack algorithms (Zhang H et al.,2020),such as FGSM (Goodfellow et al.,2015) and PGD (Madry et al.,2018).Similarly,the method of computing verified errors is the same as that used in Gowal et al.(2018),as declared in Section 3.

In this section,we focus on answering the following questions,corresponding to the next three subsections:

RQ1:Can GM-CROWN-IBP maintain state-of the-art performance in existing small perturbation tests?

RQ2: How does GM-CROWN-IBP perform in large perturbation test cases?

RQ3: How does GM-CROWN-IBP perform with different robustness weights and robustness sizes?

4.1 Performance on small perturbations

In this subsection,we compare the standard errors and verified errors of the GM-CROWN-IBP training method against state-of-the-art methods in the existing test cases,which were first proposed in IBP and then used in CROWN-IBP.

In the test cases,the training perturbations(i.e.,∊train) are relatively small.For MNIST∊train∈{0.2,0.4}and for CIFAR∊train∈{2.2/255,8.8/255}.We evaluate the models trained with Nominal(without perturbations),IBP,CROWN-IBP,and GMCROWN-IBP against different evaluation perturbations (i.e.,∊eval).In addition,we list the best error results reported in the literature for detailed comparison.The reasons for having different∊’s during the training and evaluation phases of the same network are twofold.On one hand,during the evaluation phase,we are concerned about the robustness within the perturbation radius (∊eval≤∊train),instead of only the boundary (∊eval=∊train).On the other hand,the previous methods in Gowal et al.(2018) and Zhang H et al.(2020) use the same setting,and we thus follow their settings here for fair comparisons.

Table 2 shows the evaluation results and the reported best errors in different combinations of datasets,∊trainand∊evalon models DM-large (with the MNIST dataset)and DM-small(with the CIFAR dataset).

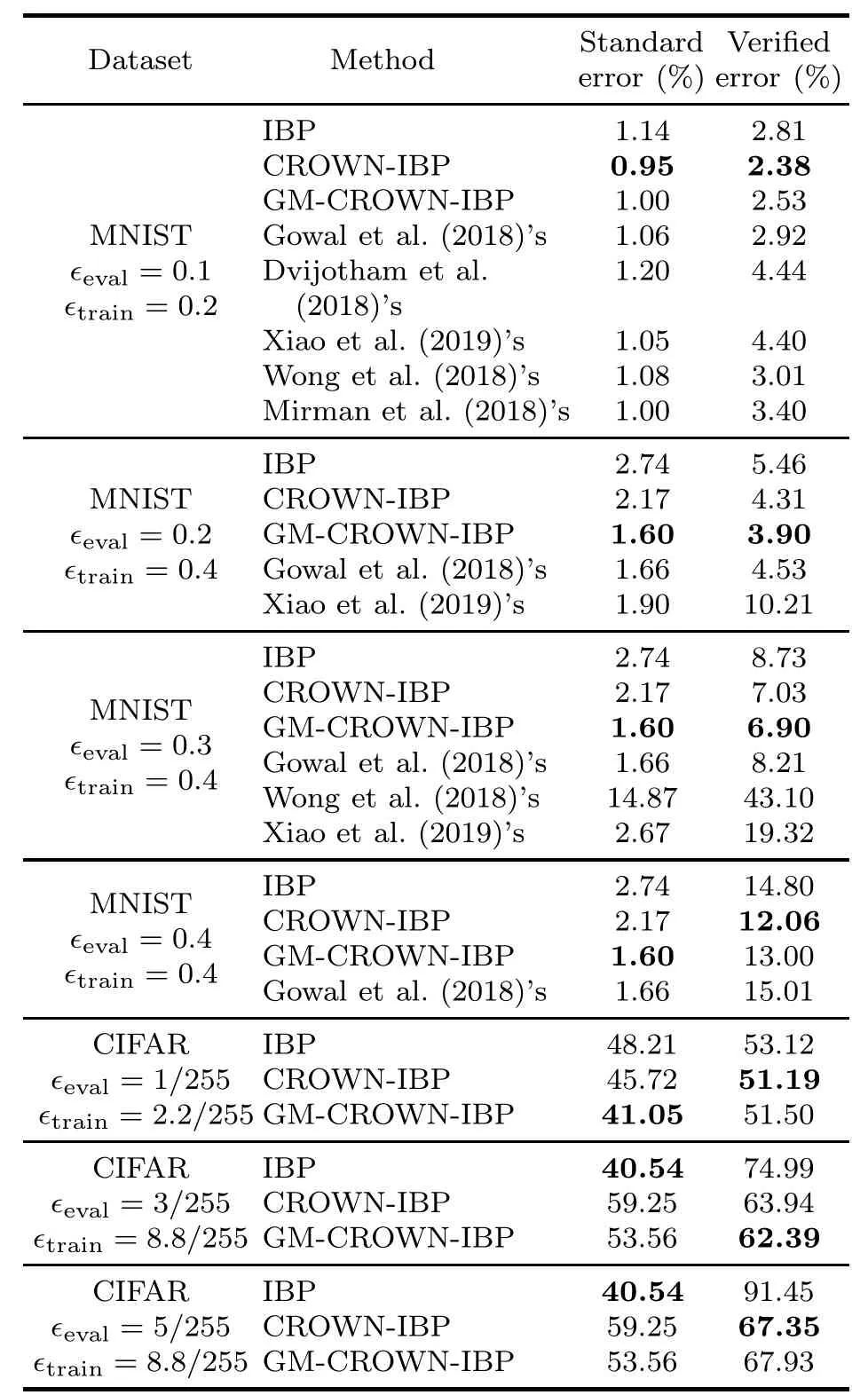
Table 2 Comparison with state-of-the-art methods in the existing small perturbation cases

It can be observed that the performance of our proposed global and monotonically decreasing robustness training strategy is close to that of CROWN-IBP and much better than that of IBP and other reported results in terms of robustness (the verified error column).It is also noteworthy that the accuracy metric (the standard error column) of the NN models trained by GM-CROWN-IBP surpasses that by CROWN-IBP obviously in most test cases,and that GM-CROWN-IBP slightly underperforms CROWN-IBP in only one case.This indicates that using the global and monotonically decreasing robustness training strategy is more likely to give balanced consideration to accuracy and robustness.

Answer to RQ1: The model robustness performance of GM-CROWN-IBP is close to that of CROWN-IBP while the accuracy is improved significantly.

4.2 Performance on large perturbations

In this subsection,we compare the standard errors and verified errors of GM-CROWN-IBP training method on large training perturbations∊train,most of which have not been tested before.For MNIST∊train∈{0.5,0.6}and for CIFAR∊train∈{17.6/255,22/255}.Similarly,we evaluate the models trained with Nominal (without perturbations),IBP,CROWN-IBP,and GM-CROWN-IBP against different evaluation perturbations∊eval.The MNIST-based network model is DM-small and the CIFAR-based one is DM-medium.

Table 3 lists the evaluation errors against different combinations of datasets,∊trainand∊eval,on the models.It can be seen that GM-CROWN-IBP outperforms IBP and CROWN-IBP in terms of both standard error and verified error metrics in almost all test cases.

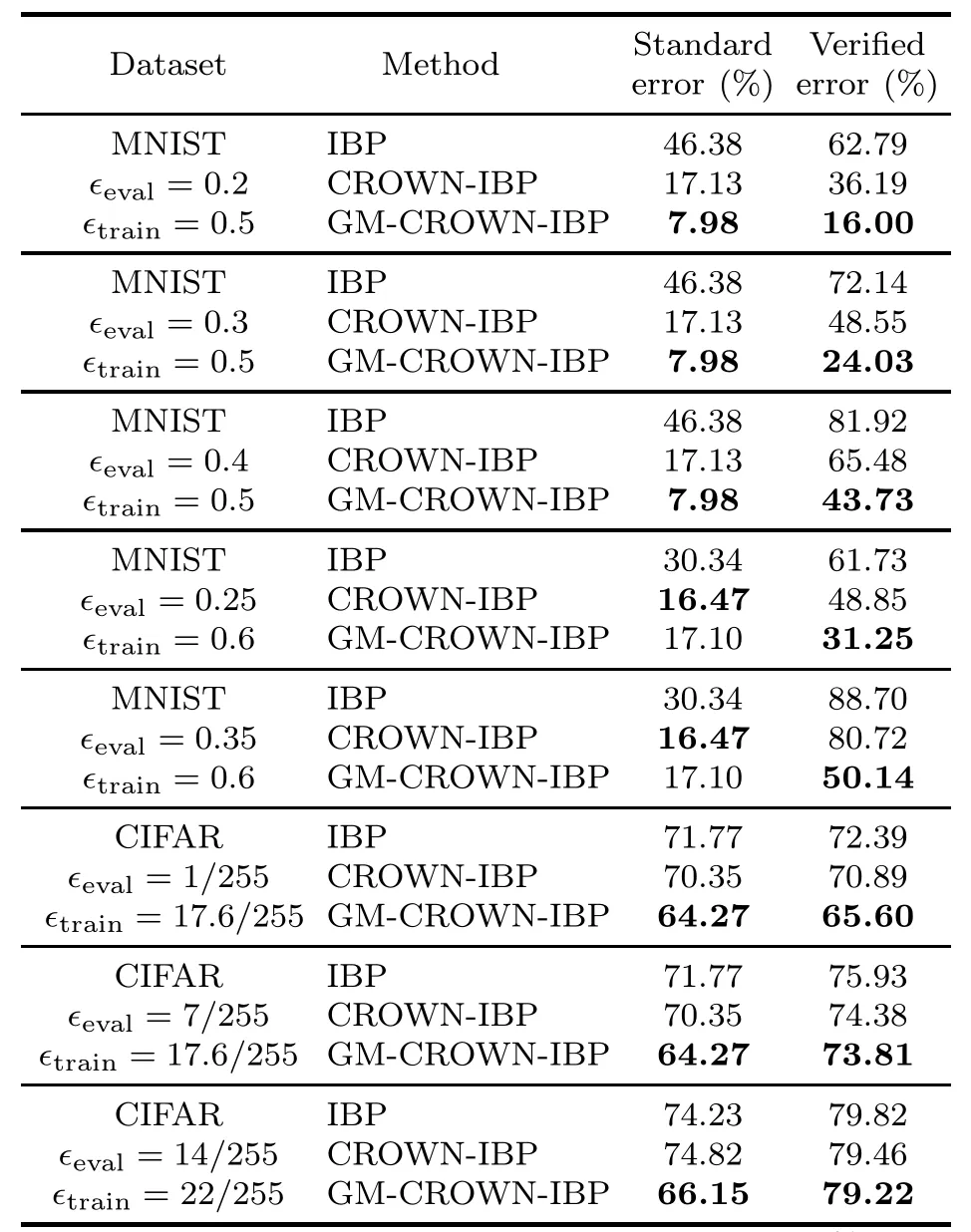
Table 3 Comparison with state-of-the-art methods against large perturbations

We also display the evaluated verified errors and total errors (summing standard and verified errors)in Fig.3.For the MNIST-based∊train=0.5 case,the verified error is shown in Fig.3a with evaluation step size 0.01 and the total error is displayed with step size 0.1 in Fig.3b.For the CIFAR-based∊train=22/255 case,the verified error is evaluated with step size 1/255 in Fig.3c and the total error is shown with step size 4/255 in Fig.3d.The label GM-C-IBP is short for GM-CROWN-IBP due to the space limit.

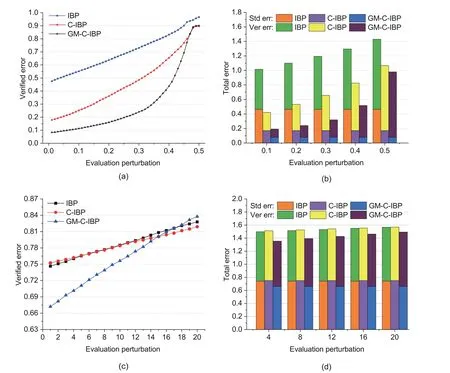
Fig.3 Alleviating the drawdown risk: (a) verified errors on MNIST with evaluation step size 0.01;(b) total errors on MNIST with step size 0.1;(c) verified errors on CIFAR with step size 1/255;(d) total errors on CIFAR with step size 4/255

As shown in Fig.3,the aforementioned drawdown risk is alleviated to a great extent and the total error remains relatively small,on both MNIST and CIFAR datasets.Strictly speaking,the verified errors of GM-CROWN-IBP are much smaller than those of IBP and CROWN-IBP on most evaluation values,which are more acceptable and tolerable in NN applications and deployment.In addition,as shown in Fig.3c,in some evaluation cases,the verified errors of GM-CROWN-IBP are a little larger.This may stem from the limitation of the IBP-family methods or the hyperparameter settings,and the verified errors might be further improved by sacrificing some model accuracy.

Answer to RQ2: The model robustness and accuracy of GM-CROWN-IBP generally outperform those of IBP and CROWN-IBP on large perturbations,and the drawdown risk is alleviated to a great extent.

4.3 Comparison on robustness weights and sizes

In this subsection,we present our tests on GMCROWN-IBP with different robustness weights and robustness sizes in the MNIST-based∊train=0.5 case,to show the compatibility of our proposed training strategy.

First of all,we carry out some experiments to illustrate the necessity of monotonic decrease in the robustness weight.Fig.4a shows the tested verified errors in four cases,i.e.,a monotonically decreasing weight (GM-C-IBP-Dec in Fig.4a),a random weight (GM-C-IBP-Ran),a monotonically increasing weight(GM-C-IBP-Inc),and the CROWNIBP baseline (C-IBP) based on the global robustness training strategy.Among these,the weights for GM-C-IBP-Dec and GM-C-IBP-Inc are 1/iand 1/(N -i)respectively,wherei ∈{1,2,···,N},andNis the robustness size,set as 10.It can be seen that the monotonically increasing weight performs in a manner similar to the random robustness weight,and that the monotonically decreasing weight outperforms the two other weight types in terms of reducing the drawdown risk (especially the evaluated verified errors in large perturbation cases).

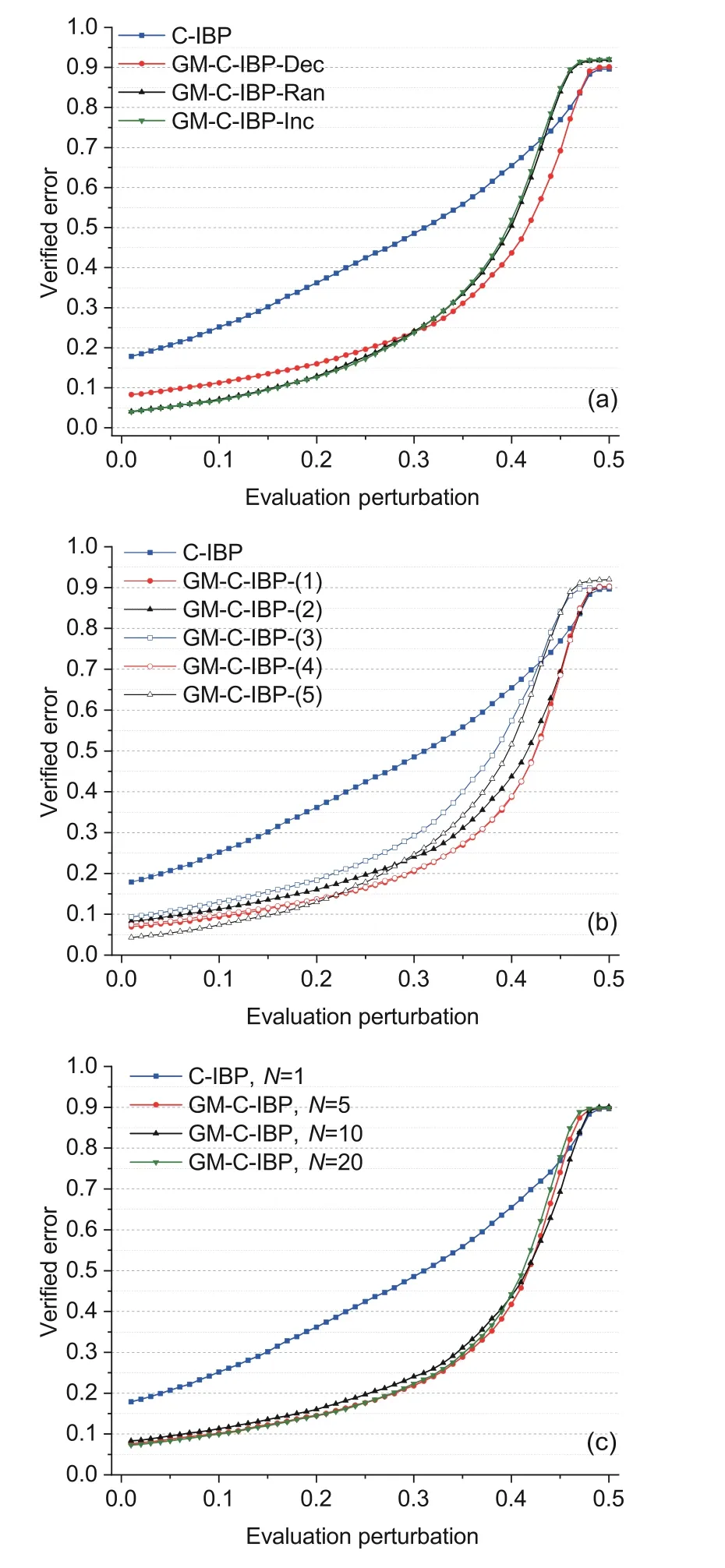
Fig.4 Performance comparisons of GM-CROWNIBP on different robustness weight types (a),monotonically decreasing robustness weights (b),and robustness sizes (c)

Furthermore,we take five types of monotonically decreasing robustness weights into account.These weightsciare (1) 1/√i,(2) 1/i,(3) 1/i2,(4)1/ln(i+1)(to avoid the division-by-zero error,1 is added to indexiin the ln function of the denominator),and (5) 1/N(constant).The first four weights are strictly monotonically decreasing,whereas the last one is not.

The verified errors of different robustness weights are displayed in Fig.4b.Compared with the CROWN-IBP baseline,all the robustness weights relax the drawdown risk,and the 1/√i-style and 1/ln(i+1)-style robustness weights work best in terms of reducing the verified error.Moreover,it is actually an ablation experiment with the robustness weight type (5) (trained only with the GRT strategy),and compared with the CROWN-IBP baseline,it can be seen that the GRT strategy has made great contributions to the alleviation of the drawdown risk,while its performance can be further improved by our monotonically decreasing robustness weight.

We also show the verified errors of GMCROWN-IBP with respect to different robustness sizesN ∈ {5,10,20}in Fig.4c.It can be observed that a large performance discrepancy does not exist among different robustness sizes.It means that a large robustness size is not necessary during the global and monotonically decreasing robustness training;thus,the concern on computation memory and duration can be eased greatly.

Answer to RQ3: The performance of GMCROWN-IBP can be further improved by the selected monotonically decreasing robustness weight,and it does not vary greatly on different robustness sizes.

Additionally,in all the training phases,GMCROWN-IBP adopts the same hyperparameter settings as CROWN-IBP to show the strengths of our training strategy.It also means that our training strategy works more stably in terms of hyperparameter selections.

5 Discussions

In this section,we discuss and explain some wellknown and related concepts or techniques that are easily confused with those in our proposed global training strategy.

5.1 Global robustness training strategy vs.global robustness

The global robustness of NNs was first defined in Leino et al.(2021),as an extension of local robustness for NNs.The global robustness captures the operational properties of local robustness for robust training,based on the utilization of global Lipschitz bounds.We refer interested readers to Hein and Andriushchenko(2017),Weng et al.(2018a,2018b),and Huster et al.(2019) for a more comprehensive view.Different from local robustness,global robustness requires that NN classifiers maintain a minimum separation margin between any pair of regions that are assigned different prediction labels.

Compared with our proposed global training strategy,the differences are mainly twofold.First,the global training strategy is a training method,instead of a newly defined robustness type,whereas global robustness is a robustness description on NNs and there have been some existing training methods on top of it (Leino et al.,2021).Second,in this paper,rather than global robustness,our global training strategy is applied to the more widely used local robustness of NNs.

5.2 Global robustness training strategy vs.randomized smoothing

In recent years,researchers also proposed some robust training methods that provide stochastic guarantees on the robustness property of NNs;that is,NNs tend to be robust with a high probability.Randomized smoothing(Cohen et al.,2019;Lecuyer et al.,2019)is one of the most representative methods.By contrast,our global training method provides deterministic robustness guarantees,like the well-known IBP and CROWN-IBP,which are more acceptable in safety-critical domains.However,randomized smoothing is generally estimated with a false positive rate around 0.1%(Cohen et al.,2019),meaning that there exist thousands of incorrectly certified instances,and this result is less reliable and tolerable.Moreover,randomized smoothing requires a large number of evaluated sample instances(as many as 10 000 samples (Cohen et al.,2019)),which may greatly deteriorate the computation efficiency.

6 Conclusions

In this paper,we focus on alleviating the unexpected drawdown risk encountered in IBP-family robust DNN training methods.First,we introduce multiple sub-perturbations into the training epochs to consider robustness with respect to some certain perturbations globally.Subsequently,we organize different robustness loss values in a monotonically decreasing style to further improve the training performance.Experimental evaluations show that the training strategy significantly reduces the drawdown risk and maintains the original performance on small perturbations.Furthermore,our proposed global and monotonically decreasing robustness training strategy obtains surprising performance on model accuracy.

In future work,we will consider further optimization of the training duration and burdens,such as the utilization of a parallel computation mechanism and a more memory-saved estimation on the robustness margin.

Contributors

Zhen LIANG designed the research.Taoran WU,Wanwei LIU,Bai XUE,Wenjing YANG,Ji WANG,and Zhengbin PANG improved the research design.Zhen LIANG and Taoran WU implemented the experiments.Zhen LIANG drafted the paper.Wanwei LIU,Ji WANG,and Taoran WU helped organize the paper.Zhen LIANG revised and finalized the paper.

Compliance with ethics guidelines

Ji WANG is an editorial board member ofFrontiers of Information Technology&Electronic Engineering,and he was not involved with the peer review process of this paper.Zhen LIANG,Taoran WU,Wanwei LIU,Bai XUE,Wenjing YANG,Ji WANG,and Zhengbin PANG declare that they have no conflict of interest.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Appendix: Hyperparameter settings with respect to IBP and CROWN-IBP on the MNIST and CIFAR datasets

Here we supplement the detailed hypermeter values for reproducing the experimental results reported in the paper.The hyperparameters are associated with the codes provided in https://github.com/huanzhang12/CROWN-IBP.Tables A1 and A2 list the hyperparameter settings with respect to training methods IBP and CROWNIBP on the MNIST and CIFAR datasets,respectively.The models used in the Methodology and Experiments sections are the same NN models trained with these hyperparameters.

It is worth noting that the GM-CROWN-IBP hyperparameter values are omitted here,because GM-CROWN-IBP adopts the same hyperparameter values as CROWN-IBP.