吴起地区延10段致密砂岩储层孔隙结构及分形特征
刘阳, 庞雄奇*, 丁超, 陈迪, 李敏
(1.中国石油大学(北京)油气资源与探测国家重点实验室, 北京 102249; 2.中国石油大学(北京)地球科学学院, 北京 102249;3.西安石油大学地球科学与工程学院, 西安 710065)
随着常规油气资源的不断勘探开发和能源需求的日益增加,勘探目标已经从常规油气资源领域转向非常规油气资源领域,非常规油气资源潜力巨大,致密油气作为其中重要的类型之一,勘探开发前景广阔,成为近年来的关注重点[1-3]。致密砂岩储层是致密油气赋存的重要场所,具有孔隙结构复杂、非均质性强的特点,复杂的孔隙结构和较强的非均质性使得储层的储集能力和渗流能力显著降低,不利于油气流动和充注,增加了致密油气勘探开发的难度[4-6],因此厘清致密储层的孔隙结构和非均质性对指导致密油气勘探开发具有重要意义。孔隙结构的复杂性和不规则性使得采用欧几里得几何等传统方法难以进行定量表征[7],分形维数成为定量表征储层孔隙结构和非均质性的重要手段。分形理论最早由Mandelbrot[8]提出,用于表征不规则几何体的自相似性,最早仅应用于数学领域,后来逐渐被引入到地质学领域中,用于表征储层孔隙结构的非均质性。贺承祖等[9]基于分形几何理论,推导出了储层毛细管压力曲线的分形几何公式,并将推导结果应用于四川盆地三叠系储层中,研究结果表明各样品具有良好的分形特征,分形维数计算公式得到了很好的应用,目前分形理论已被广泛应用于砂岩、碳酸盐岩和页岩储层非均质性研究中。
除高压压汞实验外,核磁共振、低温N2吸附、岩石电子计算机断层扫描(computed tomography,CT)和扫描电镜等实验结果也可用于计算分形维数[10-13],刘航宇等[14]根据高压压汞实验结果研究伊拉克油田Mishrif组碳酸盐岩储层的分形特征和地质意义,并结合分形特征和高压压汞曲线对储层类型进行划分,结果发现分形曲线存在“单段型”和“多段型”两种类型,“多段型”的分形曲线分别代表了不同孔喉大小的分形特征,定量描述了储层的孔隙结构特征。吴国铭等[15]根据磁共振实验获得的T2谱曲线计算了安岳气田龙王庙组和灯影组碳酸盐岩储层不同弛豫时间段的分形维数,不同弛豫时间段内各个分形维数的差值很小,采用不弛豫时间段分形维数的算术平均值作为该样品的分形维数。徐祖新等[16]根据扫描电镜图像数字化处理获得的参数计算了中扬子地区下寒武统水井沱组页岩储层的分形维数,并讨论了分形维数与总有机碳(total organic carbon,TOC)含量和储层物性的关系,结果发现孔隙类型和孔隙形态都会影响页岩储层的分形特征,孔隙类型相同而孔隙形态不同和孔隙形态相同而孔隙类型不同的页岩储层均具有不同的分形维数。三叠系延长组和侏罗系延安组为吴起地区重要的含油层系,前人已对延长组做了大量研究并进行了长期的勘探开发,而对于延安组的研究还相对较少、勘探进程较为缓慢。现主要借助高压压汞实验、X射线衍射和常规物性测试等技术手段,根据高压压汞曲线的形态和储层物性对吴起地区延10段致密砂岩储层进行分类,分析孔隙结构特征,利用分形理论计算分形维数,定量表征储层非均质性,并讨论矿物组分、储层物性和孔隙结构参数与分形维数的关系,分析分形维数的地质意义,最后进行渗透率预测。以期厘清吴起地区延10段致密砂岩储层孔隙结构和非均质性,对于明确延10段致密油气分布特征提供重要指导意义。
1 区域地质概况
研究区位于鄂尔多斯盆地伊陕斜坡中西部,总面积约7.65×103km2,勘探面积约1×103km2,如图1所示。

1为苏里格气田;2为乌审旗气田;3为榆林气田;4为神木气田;5为靖边气田;6为米脂气田;7为子州气田;8为宜川气田;9为黄龙气田;10为庆阳气田;11为红井子油田;12为胡尖山油田;13为绥靖油田;14为姬塬油田;15为靖安油田;16为安塞油田;17为吴旗油田;18为樊家川油田;19为元城油田;20为华庆油田;21为环江油田;22为华池油田;23为马岭油田;24为庆城油田;25为城壕油田;26为直罗油田;27为演武油田;28为镇北油田;29为西峰油田;30为合水油田;31为黄陵油田;32为庙湾油田
该地区地质构造条件简单,呈一个平缓的单斜构造,由东向西微倾,内部鼻状隆起发育[17-18]。延安组沉积时期,发育河流-湖泊-三角洲沉积体系,为一套重要的含油层系,分布广、埋藏浅、油藏多[19-21]。延10段位于延安组最底部,主要为辫状河沉积,砂体在纵向上叠置发育,厚度较大,物源供给主要为西北方向[21-23]。
2 样品及实验方法
研究采集鄂尔多斯盆地吴起地区延10储层12个致密砂岩样品,深度范围为1 719~1 728 m,并从采集的样品上切下部分制备成各种测试所需要的大小,进行常规岩石物性测试、高压压汞实验、X射线衍射、铸体薄片鉴定和扫描电镜分析。
常规岩石物性测试采用岩石孔隙度真空加压饱和装置和岩石渗透率测定仪进行物性测量。高压压汞实验使用Auto Pore 9250 Ⅱ压汞仪进行,测定前将样品用乙醇清洗后放置于110 ℃的烘箱中,在高温条件下抽真空干燥至恒重,除去样品中的自由水和束缚水。然后分阶段施加压力,将汞注入样品中,直至最高压力汞不能进入样品中,再开始降低压力,汞逐渐被排出,测定不同压力下的进汞量和退汞量。实验中,表面张力为0.48 N/m,接触角为140°。
X衍射全岩分析可以得到岩石的矿物组分和黏土矿物的相对含量,使用D8 FOCUS型-X射线衍射仪,在温度20 ℃,相对湿度70%的环境下进行。将样品磨制成200目的颗粒,用乙二醇在60 ℃下饱和8 h,并在500 ℃加热2.5 h,进行矿物成分分析。
岩石铸体薄片鉴定使用UB200i型偏光显微镜进行岩石薄片观察,放大倍数为40~1 000倍,实验在温度为25 ℃,相对湿度为60%环境下进行。进行铸体薄片鉴定时,将样品使用全自动磨片机磨制成2 cm×2 cm×0.5 cm的薄片,浸渍茜素红染色剂,并在分析前将薄片厚度研磨至0.04 mm。
扫描电镜的放大倍数比较大,能够清楚地识别出较小的孔隙和矿物成分,扫描电镜实验使用的是Quanta 400 FEG场发射扫描电子显微镜,加速电压为0.2~30 kV,放大倍数为7~2×106倍,图像分辨率小于或等于1.5 nm,在温度为20 ℃、相对湿度为70%、气压为0.098 1 MPa的环境下进行。
3 实验结果
3.1 孔隙类型
铸体薄片和扫描电镜观察发现,吴起地区延10段储层孔隙类型主要为原生粒间孔和次生溶蚀孔[图2(a)],少量晶间孔和粒内微裂缝,面孔率为3%~12%,平均为6.7%。粒间孔分布于矿物颗粒间,部分孔隙被铁方解石、铁白云石和高岭石、伊利石、绿泥石等黏土矿物充填[图2(b)、图2(c)],导致孔隙结构变复杂、连通性变差。溶蚀孔是由大气淡水的选择性溶蚀所形成,主要为长石溶孔和岩屑溶孔[图2(d)、图2(e)],大小不均匀,形状不规则。晶间孔主要分布在黏土矿物间,研究区晶间孔主要分布在高岭石之间[图2(f)],孔径较小,通常小于 2 μm。还可以观察到颗粒内少量碎屑溶蚀产生的粒内微裂缝[图2(g)]。喉道主要为片状和弯片状喉道[图2(h)],偶见缩颈形喉道[图2(i)]。

图2 吴起地区延10储层孔隙类型Fig.2 Pore types of Yan 10 reservoir in Wuqi area
3.2 孔隙结构特征
根据延10段12块样品的压汞曲线形态和储层物性,结合致密砂岩储层分类标准[25],将储层孔隙结构划分为3种类型,如表1和图3所示,分析孔隙结构特征和分形特征。

表1 岩石样品物性及高压压汞参数
Ⅰ类储层的物性最好,平均孔隙度和渗透率分别为13.2%和0.469 mD,排驱压力最小,小于1 MPa,最大进汞饱和度平均为81.25%。进汞初期,压力较小,汞进入较大的孔喉中,进汞曲线表现为平台段,平台段位置最低,表明该类储层孔喉分选较好,粗歪度。在汞饱和度达到50%左右时,进汞曲线开始变得陡峭,汞在较大压力下开始进入较小孔喉中。对比三类储层的累积进汞量曲线,可以看出,在相同压力范围内,该类储层汞饱和度在后期增长最为缓慢[图4(a)],表明小孔喉比例较小。汞主要位于半径为0.2~0.8 μm的孔喉中,孔喉中进汞量与渗透率贡献曲线有较大的重合,表明大喉道不仅提供了流体的渗流路径,而且有助于形成一定的储集空间。
Ⅱ类储层的物性比Ⅰ类差,平均孔隙度和渗透率分别为10.9%和0.168 mD,排驱压力较大,为 1~2 MPa,最大进汞饱和度平均为80.93%。进汞曲线平台段相比Ⅰ类储层长,但位置较高,表明该类储层孔喉分选好,细歪度。在汞饱和度为60%左右时,进汞曲线开始变得陡峭。在汞进入后期,压力相同范围内,汞饱和度比I类储层增加得更快[图4(b)],表明小孔喉占比增加。汞主要位于储层中半径为0.1~0.8 μm的孔喉中,孔喉中进汞量与渗透率贡献曲线的重合部分和峰值明显减小,表明大喉道不但提供的储集空间减小,而且对流体渗滤通道的贡献也在减小。
Ⅲ类储层物性较差,平均孔隙度和渗透率分别为8.6%和0.136 mD,排驱压力最高,大于2 MPa,最大进汞饱和度平均为60.09%。进汞曲线位置更高,呈缓慢上升的趋势,没有明显的平台段,表明该类储层孔喉分选差,粗歪度。进汞后期,汞饱和度增长最快[图4(c)],表明该类储层中小孔喉占比最大。汞主要位于半径为0.08~0.3 μm的孔喉中,孔喉中进汞量与渗透率贡献曲线的重合度很小,表明大喉道对流体的渗滤通道和储集空间的贡献非常小。
3.3 分形特征
3.3.1 分形理论
致密砂岩储层具有较强的非均质性,通常采用分形维数定量表征,其大小与孔隙表面的粗糙程度有关[26-28]。若孔喉具有分形特征,分形维数介于2.0~3.0,越接近3.0,孔隙结构越复杂,非均质性越强;相反,孔隙结构越简单,非均质程度越低[29-32]。贺承祖等[9]基于高压压汞实验结果推导出分形维数的计算表达式为

(1)
式(1)中:S为润湿相饱和度,%;Pc为毛管压力,MPa;Pmin为最大孔隙对应的毛管压力,MPa;D为分形维数。
对式(1)两边同时取对数可得
lgS=(3-D)lgPmin+(D-3)lgPc
(2)
由式(2)可知,具有分形特征的储层lgS与lgPc呈线性关系,分形维数通过该直线的斜率K求得
D=K+3
(3)
式(3)中:K为lgS与lgPc直线的斜率。
3.3.2 分形结果
根据上述分形理论,结合岩石样品的高压压汞实验结果,计算分形维数。典型样品的分形曲线如图5所示,可知,lgS与lgPc的拟合效果较好,表明这些样品具有分形特征,可以采用分形理论来表征其非均质性。分形曲线被一个明显的拐点分成两段,即存在两个分形区域,对应地就可以得到两个分形维数D1和D2,分别代表较大孔喉和较小孔喉的复杂程度。
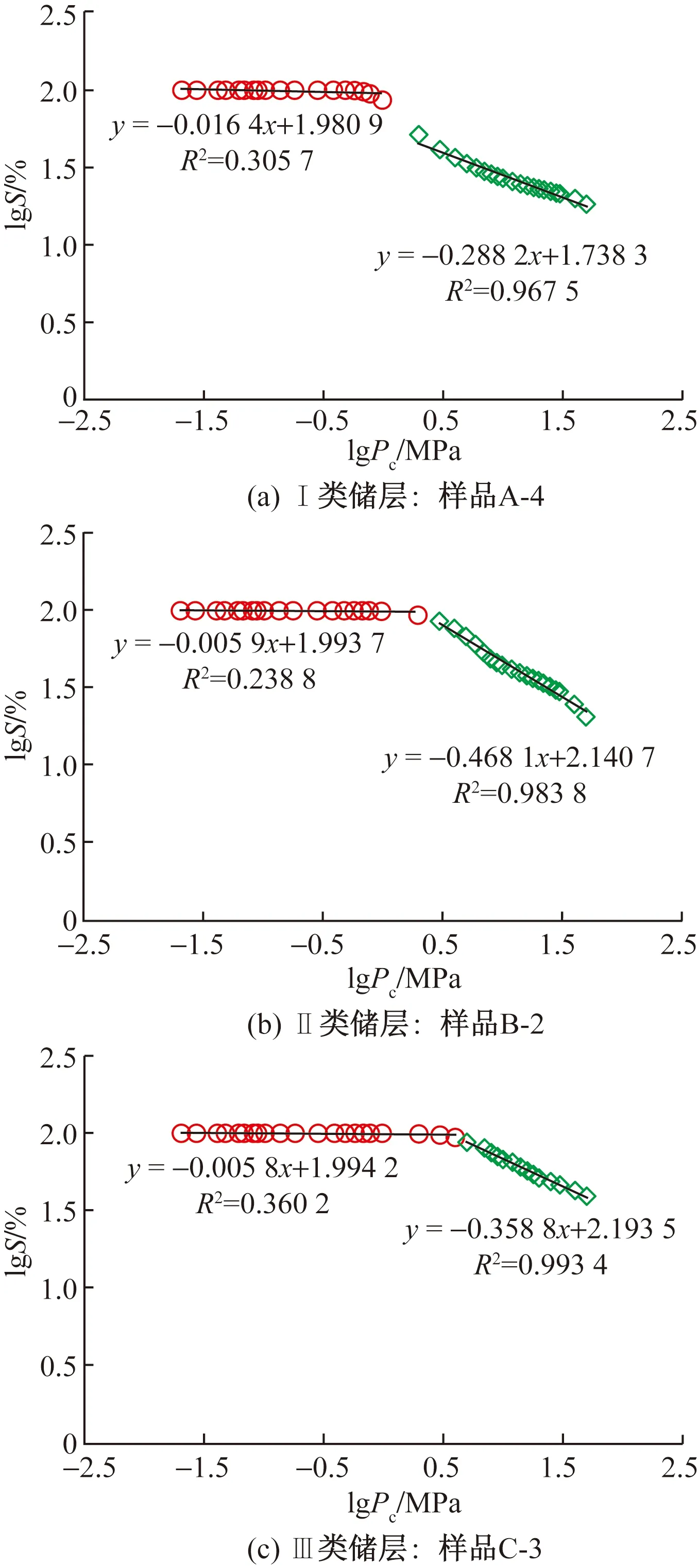
图5 不同类型储层典型样品分形特征Fig.5 Fractal characteristics of typical samples of different type reservoirs
分形维数计算结果见表2,Ⅰ类储层分形曲线转折点处的毛细管压力为1.26 MPa,D1较大,非均质性极强,孔喉结构极其复杂,为2.982 8~2.996 4,平均为2.990 4,D2较小,非均质性中等,孔喉结构复杂,为2.537 2~2.743 7,平均为2.662 4。Ⅱ类储层分形曲线转折点处的毛细管压力 2.51 MPa,D1非常大,为2.994 1~2.999 4,平均为2.996 8,D2较小,为2.454 7~2.563 1,平均为2.516 6。
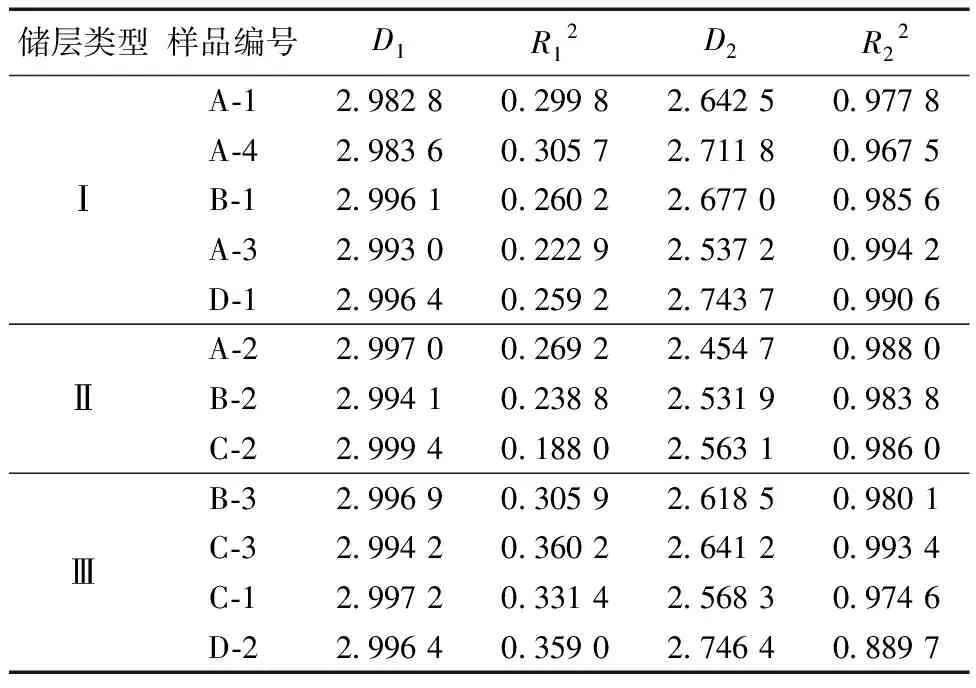
表2 岩石样品分形维数计算结果
Ⅲ类储层分形曲线转折点处的毛细管压力为5.01 MPa,D1为2.994 2~2.997 2,平均为2.996 2,D2为2.568 3~2.746 4,平均为2.643 6。
整体而言,延10段储层的分形维数较大,均大于2.4,大孔喉的分形维数D1大于小孔喉的分形维数D2。三类储层的D1为2.982 8~2.999 4,平均为2.993 9,D2为2.454 7~2.746 4,平均为2.619 7,D1的分布范围大于D2的分布范围。表明延10储层的非均质性较强,孔喉分布复杂,大孔喉的非均质程度比小孔喉的非均质程度更强,大孔喉的分布频率高于小孔喉的分布频率,储层主要受大孔喉的控制。从Ⅰ类储层到Ⅲ类储层,分形曲线转折点处的毛细管压力增大,孔喉半径减小,孔喉结构变复杂。
4 讨论
4.1 分形维数与矿物组分的关系
储层中不同矿物组分的含量差异会导致孔隙结构的复杂程度和非均质程度不同,表现为分形维数大小不同。分别拟合分形维数与石英、长石、方解石以及黏土矿物含量的关系,明确矿物组分对储层非均质性的影响。
分形维数D1与各矿物组分含量之间的相关性较好,而分形维数D2与各矿物组分含量之间没有明显的相关性(图6、图7)。D1与石英、长石含量呈负相关,相关系数R2分别为0.588 0和0.681 3。石英和长石表面比较光滑,并且石英颗粒表面比较稳定,能够抵抗风化破坏,长石容易被溶蚀形成溶蚀孔,使孔隙之间连通性增强。因此,石英和长石含量越高,孔喉表面越光滑,孔隙结构越简单,分形维数越小,非均质性越弱。分形维数与方解石和黏土矿物含量呈正相关,相关系数R2分别为0.456 9和0.499 4。碎屑岩中,方解石通常作为胶结物出现,其含量的增加会堵塞孔喉,使孔喉变小,孔隙形态也会发生改变,连通性降低,孔隙结构变差,分形维数增大。黏土矿物遇水后容易发生膨胀,造成孔隙变小,连通性变差,因此黏土矿物含量越高,孔隙结构越复杂,分形维数增大。扫描电镜分析结果表明,研究区普遍存在自生高岭石和丝状伊利石充填在孔隙中,会使孔喉变小及连通性变差。

图6 分形维数D1与矿物组分的关系Fig.6 Relationship between D1 and mineral composition

图7 分形维数D2与矿物组分的关系Fig.7 Relationship between D2 and mineral composition
4.2 储层物性与分形维数的关系
储层物性的好坏不仅受岩石自身性质影响,还与储层孔喉结构的复杂程度密切相关。分别拟合分形维数与孔隙度、渗透率的关系,结果发现,孔隙度和渗透率与D1呈负相关关系,而与D2无明显相关性(图8),表明延10储层储集能力和渗流能力主要受大孔喉复杂程度的控制。随着分形维数的增加,孔喉结构变复杂,储层中小孔喉占储集空间的比例增加,孔喉偏细歪度,非均质性增强,孔隙表面粗糙程度增加,连通性变差,储层储集能力和渗滤能力降低,孔隙度和渗透率变小。D1与渗透率的相关性(R2=0.677 3)好于孔隙度(R2=0.617 3),表明延10段储层中大孔喉的复杂程度对流体的渗流能力影响大于对储集能力的影响。

图8 储层物性与分形维数的关系Fig.8 Relationship between reservoir physical properties and fractal dimension
4.3 孔喉结构参数与分形维数的关系
为了进一步研究孔喉结构对分形维数大小的影响,拟合分形维数与最大进汞饱和度和平均孔喉半径的关系,两者均与D1呈负相关关系,与D2无明显相关性(图9)。高压压汞实验为非润湿相汞克服孔喉内毛细管阻力驱替润湿相的过程,汞饱和度既能反映岩石在一定压力下的储集能力,也能表征渗透能力[33-34]。分形维数大的储层具有更强的非均质性,在相同压力下,汞越难进入孔喉中,汞饱和度就会减小。平均孔喉半径与D1之间的相关系数为0.545 3。大孔喉的分形维数越大,汞进入孔喉中所需的压力就越大,由Laplace公式可知,平均孔喉半径就越小。

图9 孔喉结构参数与分形维数的关系Fig.9 Relationship between pore throat structure parameters and fractal dimension
4.4 渗透率预测
由渗流理论可知,流体渗流性质主要受特征长度的控制,决定了储层中流体的流动性和导电性[35]。渗透率估算模型[36]基于渗流理论,认为渗透率与孔隙度和特征长度之间的关系可以表达为
lgK=a+blgr+clgφ
(4)
式(4)中:K为渗透率,mD;φ为孔隙度,%;r为特征长度,某种孔喉半径参数可以为rd、rapex、rave、r20、r30、r35、r50等,rd为分形曲线上拐点处对应的孔喉半径,μm;rapex为汞饱和度与汞饱和度/毛管压力曲线交会图上顶点处所对应的孔喉半径,μm;rave为平均孔喉半径,μm;r20、r30、r35、r50为汞饱和度为20%、30%、35%、50%对应的孔喉半径,μm。
分别将渗透率、孔隙度与不同的特征长度进行多元回归,对应可以得到不同的渗透率预测表达式,并将计算得到的渗透率值与实测渗透率值进行比较。结果发现,以平均孔喉半径rapex为特征长度时,预测渗透率值与实测渗透率值的相关性最好,相关系数为0.664 9(图10),渗透率预测表达式为

图10 预测渗透率与实测渗透率之间的关系Fig.10 Relationship between predicted and measured permeability
lgK=-3.54+1.01lgrave+3.39lgφ
(5)
式(5)中:K为渗透率,mD;rave为平均孔喉半径,μm;φ为孔隙度,%。
5 结论
(1) 根据高压压汞曲线的形态和储层物性,将储层划分为3种类型,从Ⅰ类到Ⅲ类,排驱压力逐渐增大,物性逐渐变差,孔隙体积逐渐减小,孔喉进汞量和渗透率贡献峰值向左移动,孔隙结构逐渐变差。
(2) 吴起地区延10段致密砂岩储层孔喉具有分形特征,分形曲线存在明显的拐点,对应得到两个分形维数,D1大于D2。D1平均为2.993 9,D2平均为2.619 7,大孔喉的非均质性比小孔喉的非均质性更强。
(3)矿物组分、物性和孔喉结构主要影响大孔喉的非均质性,而对小孔喉无明显影响。随着石英、长石含量的增加,大孔喉的非均质性减弱,随着方解石和黏土矿物含量的增加,大孔喉的非均质程度增强。大孔喉的非均质性越强,物性越差。最大进汞饱和度和平均孔喉半径与D1呈负相关。
——以西加拿大盆地A区块Upper Montney段为例

