球冠形屋盖平均体型系数估算研究

陈伟伟，刘毅杰，黄苗周

温州设计集团有限公司,浙江温州325000

0 引 言

随着社会经济的发展，球冠形屋盖因能够满足特定的建筑功能及建筑造型要求，越来越多地被应用于工程中［1-4］。球冠形屋盖的体型系数，明显不同于常规建筑［5-6］。《建筑结构荷载规范（GB 50009—2012）》［7］（以下简称《荷载规范》）表8.3.1给出了部分建筑物的体型系数。国内常规结构的整体建模基本采用PKPM 和盈建科软件［8］。整体模型中，对风荷载体型系数的处理基本按照《荷载规范》表8.3.1中第30项和第31项，即迎风面的体型系数基本为0.8，背风面的体型系数一般为0.5～0.6，迎风面和背风面的体型系数和基本为1.3～1.4。同时《荷载规范》表8.3.1中第36项给出了旋转壳顶的体型系数，但该系数是以平面角和仰角为变量的参数方程形式给出，在整体模型中使用并不方便。本文结合《荷载规范》，通过适当简化，近似推导出球冠形屋盖的推力合力、吸力合力及投影面积的体型系数。

1 球冠形屋盖风荷载积分推导

1.1 风荷载等效集中荷载

在《荷载规范》中，风荷载按式（1）计算

风荷载对结构的作用可分为平均风部分和脉动风部分，风荷载计算公式中的βz则主要考虑脉动风对结构的作用；公式中的μs、μz、w0则主要考虑平均风对结构的作用，其中μs主要与建筑物的形体有关。《荷载规范》表8.3.1给出了39项不同结构类型的风荷载体型系数的取值，对于常规结构体系，结构整体计算时，体型系数常按表中第30 项和第31 项取值。但对于球冠形屋盖，其风荷载体型系数较为复杂，见《荷载规范》表8.3.1中第36项（图1）。其中，f/l ＞1/4，μs=0.5 sin2φ sin ψ -cos2φ；f/l ≤1/4，μs=-cos2φ，ψ为平面角，φ为仰角［7］。

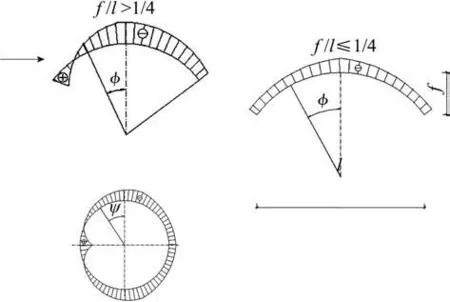
图1 风荷载体型系数[8]

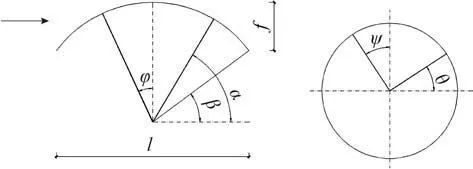
图2 球冠形屋盖平面角与仰角位置

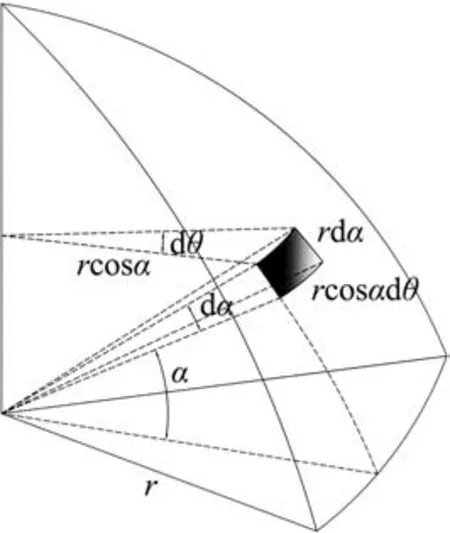
图3 微元面积示意

对于球冠形屋盖的某一测点，其风荷载计算公式为

则该点微元面积dA上的风荷载集中力的大小为

1.2 沿投影面积的平均体型系数μs

上文中已经得到了风荷载等效集中荷载的计算公式，但在工程常用的结构分析软件中，需要给出一个μs，结构分析软件才能对风荷载进行计算分析。此外，常用软件在对该类结构体型的风荷载计算中，涉及的风荷载作用面的取值往往采用投影面积。为此，可以根据μs=∫μsidA/Ae，进一步得出沿投影面积的平均体型系数μs。

图4为球冠形屋盖各方向投影面积图，可以推导出起始角度β与f/l 之间的关系。

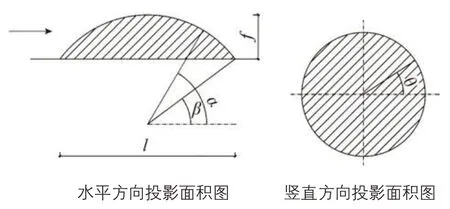
图4 球冠形屋盖各方向投影面积

从图5可以发现，f/l 随着起始角度β的增加而降低。

图5 起始角度β与f/l 关系

1.3 球冠形屋盖风荷载快速计算表

图6 为球冠形屋盖起始角度β 与F'x、F'y、F'z之间的关系图，可以发现，随着起始角度的增大，球壳表面积逐渐减小，故F'x与F'z均逐渐减小。

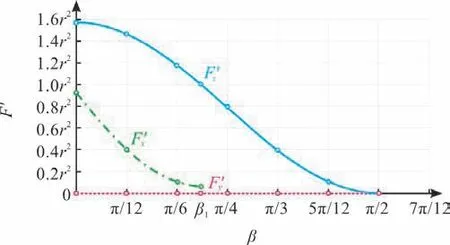
图6 球冠形屋盖起始角度β与F x、F y和F z之间的关系

将图6数值除以对应方向的投影面积，即可得出球冠形屋盖起始角度β与平均体型系数μsx、μsy和μsz之间的关系图（图7），可以发现：1）在0～β1区间，μsx值由0.589降至0.143；在β1～90°区间段始终为0。2）μsy值始终为0。由图1可知，在风荷载作用下，横风向方向的风吸力为对称分布，故合力为0。3）随着起始角度β的增加，μsz的绝对值由0.5增大至1。

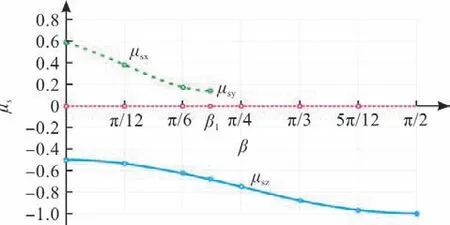
图7 球冠形屋盖起始角度β与μsx、μsy和μsz之间的关系

为了方便计算，表1中列出几种典型球冠形屋盖起始角度的结构风荷载计算系数。

表1 球冠形屋盖风荷载快速计算

1.4 有限元算例

通过sap2000对标准半球形进行建模，半球半径为16 500 mm，将该结构在水平角与仰角方向进行网格划分，其中水平角角度间隔30°，仰角间隔9°。针对每一板单元，其μs取值为板单元形心处的μs，并将其均匀施加于板单元上，且其方向垂直于板单元。具体μs分布见表2 和图8，分析计算结果对比见表3。

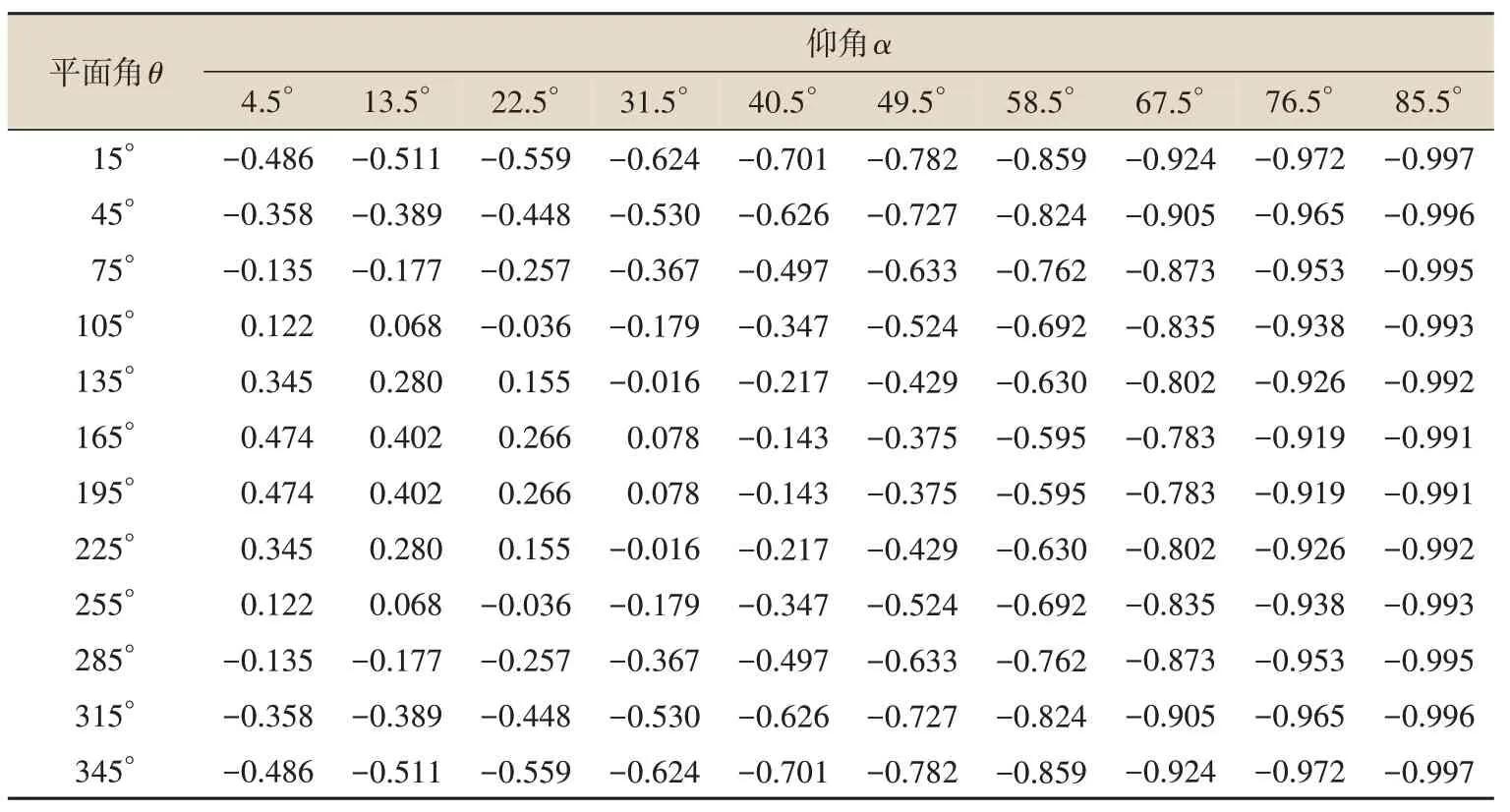
表2 各板单元形心处的μs值

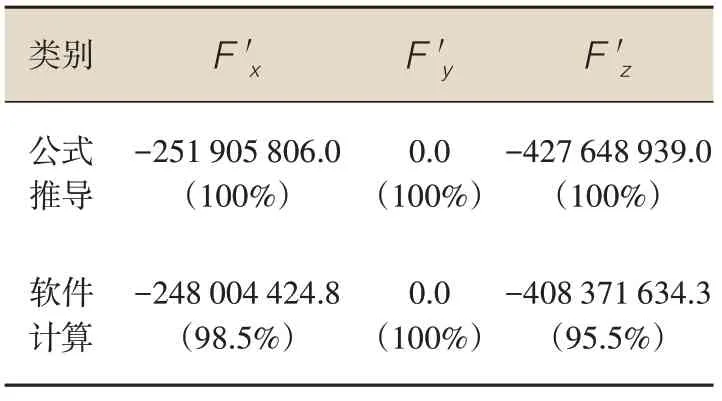
表3 标准半球屋盖风荷载合力对比

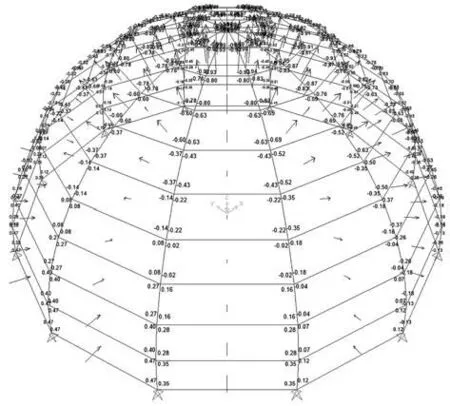
图8 标准半球屋盖风荷载体型系数分布

通过表2的数据对比可以看出，有限元结果与本文公式基本吻合。

2 结 论

本文基于《荷载规范》旋转壳顶的风荷载体型系数公式，通过假定βz和μz取高度范围内的平均值从而简化公式，对球冠形屋盖进行计算，得到了风荷载等效集中荷载的计算公式及沿投影面积的平均体型系数μs。结果表明：

1）风荷载作用下，沿顺风向投影面积的平均体型系数介于0～0.59 之间，远小于常规建筑的1.3～1.4。

2）风荷载作用下，沿竖直投影面积的风吸力平均体型系数介于-1.0～-0.5之间。

对于球冠跨度较大、高度系数和风振系数不宜统一取值时，亦可按本文方法将壳面划分为高度系数和风振系数取相同值的若干块，然后分块积分求和。

本文结论可供相关工程设计参考。