高压下KNN压电性能的第一性原理计算

张 涛,陆荣浩,杨龙海,李 敏,周丽君,席 悦

(1.西安科技大学 材料科学与工程学院,陕西 西安 710054;2.西安科技大学 理学院,陕西 西安 710054;3.西安科技大学 电气与控制工程学院,陕西 西安 710054)

0 引 言

煤矿井下生产环境恶劣,其中气体环境、温度环境、光照环境、噪声环境与粉尘环境与安全生产息息相关。声表面波传感器因其灵敏度高、体积小、集成化和无线化优势明显,可以实现对煤矿井下环境全面感知应用并为煤矿井下安全生产保驾护航。压电材料能实现的力-电换能,在其表面直接制备叉指电极,便可有效地接收和发送声表面波,通过适当地选取叉指电极的间隔、数目、长度及叉指电极形状即可改变声表面波的特性,这也是声表面波器件中声学传感技术关键所在。面向声学煤矿传感技术的压电材料已有相关报道,EUN等设计了一种新型的基于声表面波的应变传感器,该传感器的应变灵敏度为2.5 kHz/%,约比同类型声表面波应变传感器的灵敏度高出5倍[1];贾雅娜等结合有限元和耦合模理论对沉积铁钴薄膜栅阵的声表面波电流传感器中的磁致伸缩效应进行分析,并对其传感响应进行仿真,确定了优化后的传感结构参数[2];张涛等以压电材料作为基底的声表面波器件,在涂覆敏感薄膜后并应用在传感器中,可识别煤矿井下有害气体如甲烷气体浓度的变化[3]。

压电材料还被广泛应用于人工智能、生物医疗、智慧家居和MEMS等领域[4-5]。2019年1月,生态环境部联合发改委、工信部等9部委联合发布《废铅蓄电池污染防治行动方案》,要求将废铅蓄电池污染防治作为治污攻坚战的重要内容,鉴于此,铌酸钾钠KNN((K0.5Na0.5)NbO3)[6]、钛酸铋钠BNT((Bi0.5Na0.5)TiO3)[7]、钛酸钡BST(BaTiO3)[8]等环境友好型压电材料受到越来越多的关注。目前对无铅压电材料性能的优化研究主要集中在掺杂改性[9]、织构化技术[10]和构建复合材料体系[11]。

KNN基压电材料是一种高性能环境友好型无铅压电功能材料,具有高压电性能d33=310 pC/N和高居里温度Tc=420 ℃等优点[12-13],利用第一性原理和相场模拟等方法预测与解释材料性能方面机理已有广泛的研究。GAO等制备了多元掺杂陶瓷,通过双球差校正电镜分析技术表征结合第一性原理和相场模拟研究KNN掺杂—结构—性能之间的关系,提出掺杂诱导的四方相和具有小角度极化矢量区的高密度纳米异质结构是导致高介电和压电性能的机制[14];LI等通过第一性原理研究发现Ca2+的引入使KNN体系带隙、费米曲面向价带移动,其相结构从O相(菱方相)转换为T相(四方相)[15];FU等研究了Sr2+掺杂KNN中缺陷偶极子与铁电畴的协同作用,使其呈现出与PZT不同的电致应变行为以及大应变[16];LIU等发现氧空位会引起KNN晶格畸变与应力失配,在保持本征压电贡献的同时抑制畴壁移动,从而有效平衡压电材料的机械品质因子与压电系数[17]。

YE等通过高压拉曼等试验方法,测试出CaSnO3掺杂NaNbO3在6.55 GPa和10.05 GPa下发生相转变[18]。KAKIMOTO等使用基于金刚石对顶砧的高压拉曼技术研究了Na0.5K0.5NbO3相结构转变,发现该体系在2.04～3.41 GPa发生了正交相-四方相相变[19]。METTA等使用第一性原理计算内的广义梯度近似对电子和局部结构的Li掺杂KNN在静水压力下进行了研究,结果表明由于A位阳离子之间的离子尺寸差异,KNLN陶瓷在0 GPa下为四方相。当材料经受外部压力5.85 GPa时转变成正交相,而在约7.20 GPa下转变成三方相[20]。

采用基于密度泛函理论(Density Functional Theory,DFT)的第一性原理计算方法,从KNN晶体结构、电子结构包含的能带和原子轨道分波态密度等方面,对不同压力下KNN的晶体结构、电子结构、介电性能和压电性能进行了研究,该研究的开展为对通过外加压力调控KNN材料的电学性能研究提供了理论参考,有利于促进声学煤矿感知技术的发展。

1 模型建立与计算方法

1.1 模型参数

(K0.5Na0.5)NbO3在绝对零度时处于三方相R相(空间点群为R3mR),在约-123 ℃时从三方相R相转变至正交相O相(空间点群为Amm2),约200 ℃从正交相O相转变至四方相T相(空间点群为P4mm)。首先分别建立R相、O相和T相铌酸钾KNbO3(KNO)初基原胞,晶胞参数见表1。

表1 不同相结构KNO晶胞参数

采用超晶胞法对KNO进行1×1×2扩胞,将1个Na原子替换1个K原子,获得R、O、T相KNN晶体理论模型[21],1×1×2的KNN晶胞中原子总数为10个,Na原子和K原子各1个,Nb原子2个,氧原子6个。K原子和Na原子以1∶1比例混合后占据不同原子位置,即KNN原胞由NaNbO3与KNbO3沿[001]方向堆叠而成。电子结构、光学特性和压电性能也都是基于O相KNN计算得到,而建立R相和T相KNN原胞并计算相应的吉布斯自由能的目的是为确定15 GPa附近相转变状态。

1.2 计算参数

基于密度泛函理论的第一性原理计算,采用维也纳从头计算模拟程序包(Vienna Abinitio Simulation Package,VASP)软件包,为平衡计算量与试验结果精度,赝势采用广义梯度近似下的PBE形式,截断能采用400 eV收敛精度为5×10-6/atom,参与计算的价态电子分别为Na-2p63s1,K-3p64s1,Nb-4p64d45s1,O-2s22p4。

2 结果和讨论

2.1 KNN晶体结构

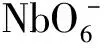
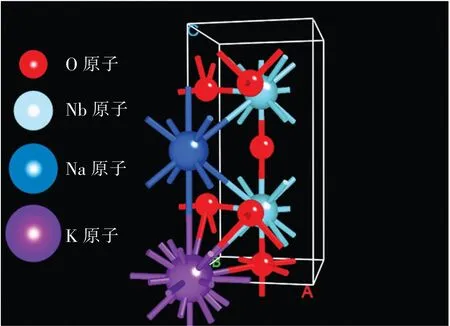
图1 O相KNN原胞模型Fig.1 Crystal structure of O phase KNN

对不同压力下O相KNN晶体结构优化自洽后的晶格常数见表2,在未加压力时,O相KNN晶格常数分别为a=3.954 75 Å,b=3.996 46 Å,c=3.995 04 Å,计算结果符合O相KNN常规晶格常数特征晶,其中a=3.994 Å与b=3.994 Å[22]。随着外加压力从0 GPa增大至21 GPa,KNN晶格常数a,晶格常数b与晶格常数c整体都趋于减小,说明KNN晶体内原子间距离减小,原子相互间库仑力增大,相互间静电作用增强。

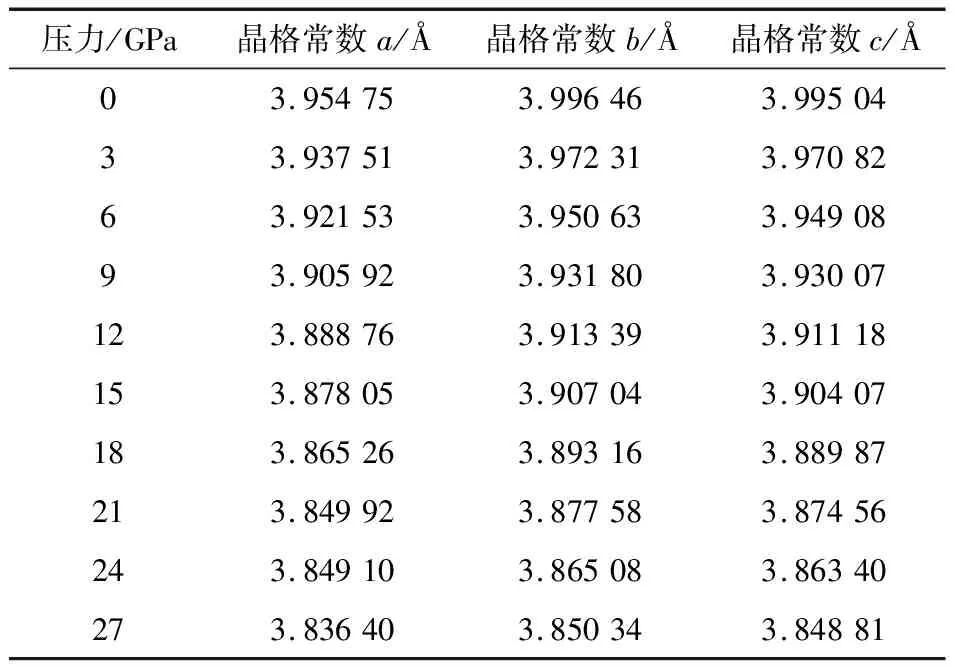
表2 不同压力下O相KNN晶格常数

图2为不同压力下O相KNN晶格常数变化关系,随着外加压力逐渐增大时,KNN的晶格常数整体趋于减小,说明KNN晶体在外加压力的作用下被压缩。

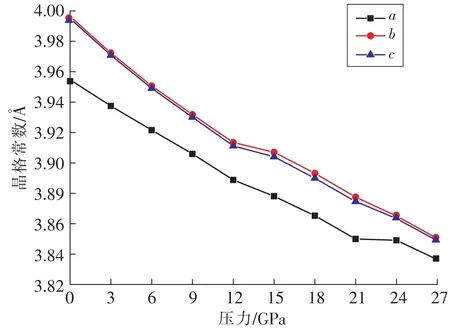
图2 不同压力下O相KNN晶格常数变化关系Fig.2 Relationship between lattice constants of O phase KNN under different pressures

2.2 KNN相组成

图3为不同压力下KNN相结构相对吉布斯自由能变化。在绝对零度下,KNN处于R相结构,以R相吉布斯能量作为0能量基准参考点,O-R曲线是KNN的O相与R相吉布斯自由能相对差值,自由能越小,体系结构越稳定[23]。从图3可以看出,未加压力时R相结构的KNN自由能最低,O相KNN次之,T相KNN最高。在0～15 GPa外加压力范围内,R相KNN自由能最低,说明KNN在该压力范围晶体结构更偏向于R相。随着压力增大,O相自由能整体呈现先增大后减小的趋势,说明KNN相结构对O相的偏向程度也是先增大后减小,当外加压力增加为18 GPa时,红色曲线代表的O-R相自由能相对差值曲线低于黑色曲线R相自由能基准线,说明该压力下O相能量达到最低即KNN在18 GPa下为O相,可以判断在外加压力为15～18 GPa范围时KNN发生了由R相到O相的转变。而在外加压力范围为18～21 GPa时,红色曲线代表的O-R相自由能相对差值曲线仍然低于黑色曲线R相自由能基准线,所以在18～21 GPa的KNN保持为O相。

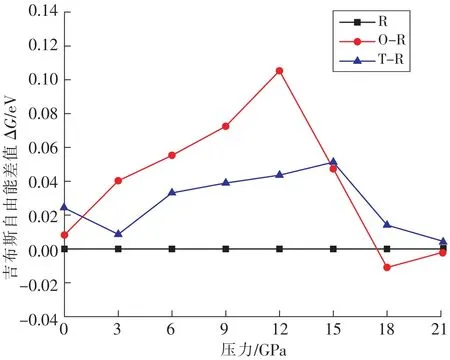
图3 不同压力下KNN相结构相对吉布斯自由能变化Fig.3 Relative ibbs free energy change of KNN phase structures under different pressures

2.3 电子结构

图4(a)为外加压力0 GPa下O相KNN在-5～5 eV能量范围内的能带图,以费米能级为界,上方能带为导带,下方能带为价带,导带底与价带顶之间的能量差即为KNN能带带隙宽度1.95 eV。KNN导带底和价带顶分别位于布里渊区高对称点G和E处,属于间接带隙半导体。

图4 O相KNN能带和带隙值变化Fig.4 Band structure of O phase KNN and changes of band gap

图4(b)为KNN能带带隙值随外加压力大小的变化图,根据Wilison相变原理,在外加压力下晶体晶格常数减小,原子间的距离减小,其导带与价带会相应展宽并且重叠程度会进一步增大,最终导致能带带隙值减小,所以当外加压力从0 GPa增大至15 GPa时,结合图2中KNN晶格常数减小原子间距离减小,带隙值从1.938 7 eV单调减小至1.873 7 eV。在外加压力为15～21 GPa时KNN的带隙增大,这是由于随着外加压力增大,晶格常数常数在不断减小,原子间的距离也在不断减小,而原子之间的相互静电作用也在增强使此压力范围内原子间成键由离子键向共价键转变,从而导致了带隙增大[24]。

图5为不同压力下KNN的原子轨道分波态密度(Density of State,DOS)。-17～-15.5 eV范围内态密度主要由O原子的2p轨道电子贡献;-12～-11 eV范围内态密度主要由K的3p轨道电子贡献,此时峰形尖锐电子局域性较强,说明K原子在KNN体系中主要以离子键形式存在;-5～0 eV范围内价带和0～5 eV范围内导带的态密度主要由O原子的2p轨道电子和B位Nb原子的4 d轨道电子贡献,Nb原子和O原子有较强的共振峰,说明O的2p轨道电子和B位Nb的4 d轨道电子产生强烈的p-d轨道电子杂化作用,Nb与O轨道电子杂化作用和Nb-O原子构成的八面体对KNN体系性能有较大影响;5～10 eV范围内态密度由Na的p轨道电子贡献,态密度峰型尖锐,主要以离子键形式存在于体系中。

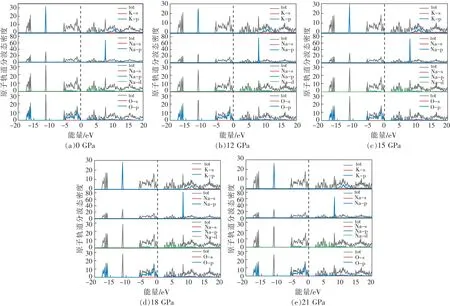
图5 不同压力下KNN原子轨道分波态密度Fig.5 Partial density of states of KNN atomic orbitals under different pressures

2.4 介电性能

在交变电场下,电介质的介电常数为复数,复介电函数见式(1)

ε=ε1(ω)+iε2(ω)

(1)

式中 实部ε1(ω)反映介电常数随频率的变化情况,虚部ε1(ω)反映材料内部的驰豫极化损耗。

图6是不同压力下KNN复介电常数,图6(a)中光子能量为0 eV时,纵坐标介电常数实部代表直流下KNN的静态介电常数,可以看出未加压时,KNN的静态介电常数为5.594 2,随着光子能量增大至3.348 7 eV时,介电常数达到最大8.112 4,光子能量增大至5.014 5 eV时,损耗达到最大6.543 8。

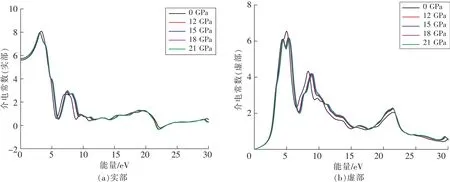
图6 不同压力下O相KNN复介电常数Fig.6 Complex permittivity constants of KNN under different pressures

随着外加压力的增加,结合图5不同压力下KNN的态密度变化可以看出,外加压力下KNN整体的介电实部与虚部发生蓝移是由于压力增大引起晶格间距减小与原子之间静电增强引起的。加压后,KNN静态介电常数由5.594 2增加到5.729 8以上,在可见光1.64～3.19 eV范围,介电常数均增大,介电虚部几乎无变化,所以KNN复介电常数增加,这有利于KNN在可见光波段的应用。结合图2不同压力下O相KNN晶格常数变化关系图与图5不同压力下KNN原子轨道分波态密度得到,介电性能的增强是由于加压后处于钙钛矿KNN结构B位的Nb原子与O原子距离更近,原子中心位置更易发生相对位移从而产生更多位移极化,B位原子与O原子p-d轨道杂化作用增强导致。

2.5 压电性能

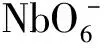
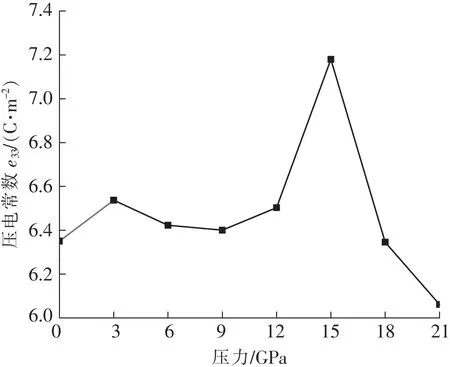
图7 不同压力下O相KNN压电性能Fig.7 Piezoelectric properties of O phase KNN under different pressures

3 结 论

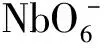
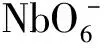
3)随着外加压力的增大,钙钛矿KNN结构B位的Nb原子与O原子中心位置更易发生相对位移从而产生更多位移极化,B位原子与O原子p-d轨道杂化作用增强,KNN的介电常数发生蓝移,复介电常数更高。在外加压力为15 GPa下的KNN具有最大的压电性能e33=7.2 C/m2。