循环荷载下黄土孔隙水压力与能量耗散演化

张 健,谢渭平,常彦博,田 丰,黄 超,祝仰明,曾彬峻

(1.中国水利水电第八工程局有限公司,湖南 长沙 410004;2.中电建铁路建设投资集团有限公司,北京 100060)

0 引 言

黄土强度的劣化通常包括2个机制:首先为结构损伤与重塑,其次为孔隙水与土的相互作用。特别是在动力环境下,孔隙水压呈现出强烈的动力效应,原因是压实黄土的导水率较差,进而其有效应力出现明显变化,表现为宏观强度降低,产生系列变形破坏[1-5]。黄土孔隙水压力的动力反应模式研究是当前岩土工程领域的难点和焦点。

饱和土孔隙水压力的动力反应研究已经取得了长足发展,所取成果诸多[6-9]。早年的研究大多关注孔隙水压力与应力或应变的关系,如SEED等基于动应力变化特征建立了反正弦三角函数模型,考虑到应力模型大多以土体发生液化时的循环荷载次数,使得经验参数的选取直接影响了模型的精确性[10]。学者们开始关注孔隙水压力与体应变的演化模式,其中最具代表性的是Martin-Finn模型[11]和汪闻韶模型[12]。应力模型受所选取参数的影响较大,应变模型对孔隙水压力动力反应机制的表征仍有局限性。NEMAT-NASSER等较早关注到地基在地震作用下孔隙水压力的增加的本质是地震波能量的耗散或转移至土骨架颗粒,导致土骨架颗粒的重新排列,并且定量研究了土体在动力作用下孔隙水压力与单位体积土体耗散能量密度之间的相关性[13]。许多学者从能量角度研究各类土体孔隙水压力动力反应,在可液化饱和砂土的相关研究中取得了良好效果[14-17]。而关于黄土这类细粒含量高的低液限黏土,其孔隙水压力的动力反应机制研究主要集中在土体的振动液化方面,如孙海妹等对兰州黄土进行空心扭剪试验,提出土体动应力动应变发展模式,界定了初始液化的临界应变值,还得到了峰值动孔隙水压力能达到初始有效固结围压的结论[18];张晓超等关注强震作用下,饱和黄土易发生液化和流滑的现象,研究不同初始物理条件下黄土孔隙水压力的动力反应规律和液化特征,发现黏粒含量越低,黄土振动孔隙水压力响应越快,液化应力比越低,但未探讨孔隙水压力的预测模型[19];杨秀娟等针对黄河三角洲粉质黏土开展不排水动三轴试验,探讨了其孔隙水压力随加载振次的演化规律和归一化模型[20]。尽管针对黄土孔隙水压力动力反应机制的研究已经取得长足发展,但研究成果多着眼于孔隙水压力与应力和应变方面展开,能够反映孔隙水压力增长机制的能量模型未见提及,有必要研究土体在循环荷载下孔隙水压力与能量耗散的潜在发展关系,并进一步建立归一化分析模型。

基于此,在现有土孔隙水压力动力响应研究的基础上,开展压实黄土不排水动三轴试验,分析不同动应力条件下,孔隙水压力与能量耗散的发展关系和演化模式,探讨基于能量发展模式的黄土孔隙水压力增长模型,揭示压实黄土的动力特性的演化与机制,为压实黄土灾害防治提供理论依据。

1 试验材料与试验方案

1.1 试验材料及试样制备

试样取自西安东郊某城市道路路基的扰动黄土,其色泽呈黄褐色,较湿,基本物理力学参数见表1。取适量土样用木碾碾碎,采用恒温烘箱干燥10 h后过2 mm筛,以最佳含水率(18%)配置湿土,按照路基土95%压实度确定干密度(1.8 g/cm3),称取适量湿土压制尺寸为φ38 mm×76 mm的圆柱形试样。

表1 黄土基本物理性质指标

1.2 试验方案

不排水动三轴试验采用Wille-Geotechnik LO7010/5DYN型动三轴测试系统完成(图1),首先对试样进行真空饱和,饱和完成后拆样并用橡皮膜封闭,然后安装至动三轴试验仪压力室基座,检测孔压系数达到0.95后进行等向和轴-径向非均等固结,待固结排水速率低于0.1 mL/h,结束固结,关闭排水阀,进行不排水动三轴剪切试验。借鉴王兰民、王铁行等针对西北黄土的动三轴试验研究结论,将试验停机条件设为试样应变幅值达到6%[21-22]。

图1 动三轴试验装置Fig.1 Dynamic triaxial test device

压实黄土动强度测试通过应变控制实现伺服加载,荷载波形为典型的简谐正弦波,结合现场取土深度确定固结围压测定值,试验固结围压为恒定200 kPa。试验采用3组压实黄土含水率,分别为5%、15%、20%,黄土试样的3组压实度分别设置为85%、90%、95%。基于车辆荷载频率属于低频荷载,室内试验设置0.5,1,1.5 Hz不同频率的荷载。

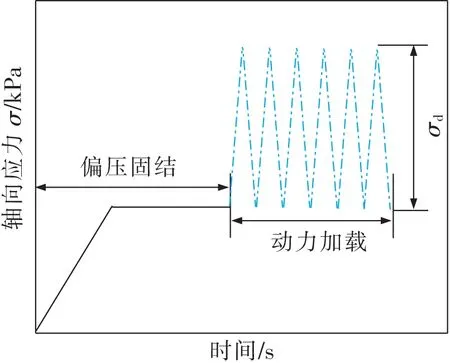
图2 加载方案示意Fig.2 Schematic diagram of loading

鉴于目前研究将交通荷载频率设置为1 Hz时,能够较好地分析路基土的动力行为。因此,采用频率为1 Hz,分析循环应力比CSR和固结应力比Kc的影响效应,试验方案设置见表2。

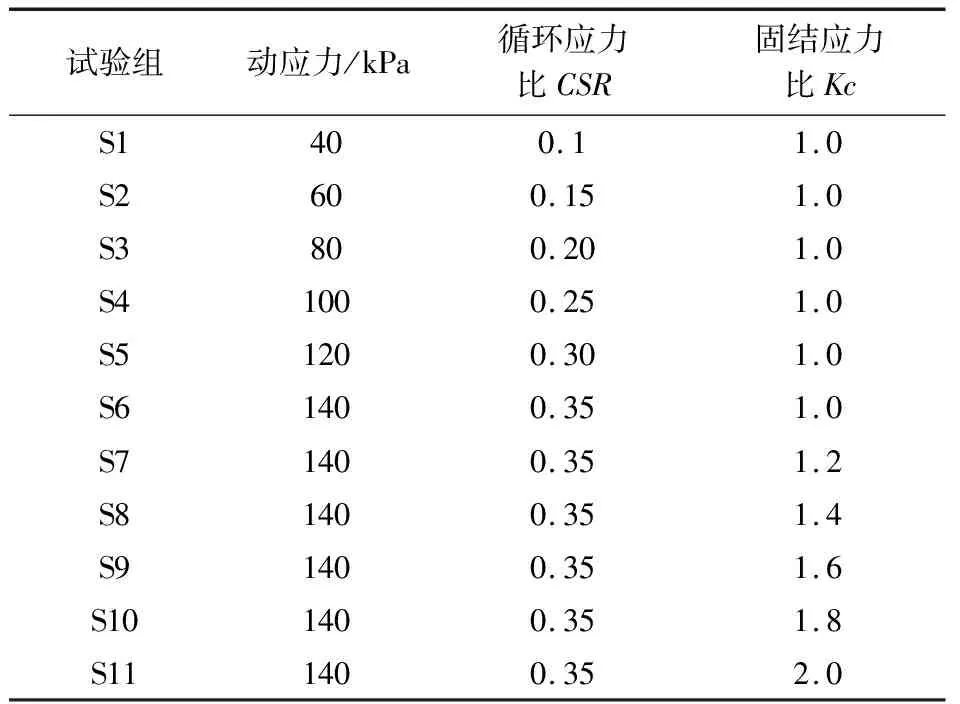
表2 动三轴试验方案

压实土体孔隙水压力的动力反应本质上是受到振源振动能量激发的一种客观表现。鉴于车辆动载下土体孔隙水压力具有循环累积效应,取每个循环加载周期内的一个平衡孔隙水压力upi作为孔隙水压力平衡状态点,第i周的平衡孔隙水压力upi可由该次循环加载期间孔隙水压力的最大值ui,max和最小值ui,min加权平均求得,计算式为

upi=(ui,max+ui,min)/2

(1)

同理,第i个加载周期内,土体塑性累积应变εpi也可写为

εpi=(εi,max+εi,min)/2

(2)

式中εi,max和εi,min分别为第i个循环加载期间土体累积塑性应变的最大值和最小值。

动应力为σd的循环荷载下,单位土体在第i个循环加载周期内产生的塑性应变累积能量耗散Wpi的计算式为

Wpi=σdεpi

(3)

土体在循环加载期间产生的黏滞累积能量耗散计算的传统方法是对滞回圈所围成图形进行面积计算,计算时多采用椭圆曲线对滞回圈拟合求解,但测试得到的滞回圈是不规则形状,计算繁琐且误差大[24]。鉴于此,遵循陈伟等描述的方法,选取应力-应变平面获取的相应数据点形成的多边形面积作为骨干曲线滞回圈的面积[25]。试验期间,每个循环周期内采集20组应力应变数据,根据空间解析几何规则,第i个循环加载期间应力应变滞回圈的面积可表示为

(4)

式中 第j个周期动应力为σjd,相应的应变为εjd。

第i个加载周期内土体因黏滞效应所产生的累积能量耗散Wri为

(5)

2 试验结果与分析

2.1 不同频率下黄土动水压力

测试压实黄土试样含水率处于最优含水率18%,干密度为1.8 g/cm3时,不同荷载频率条件试样的动强度变化规律,图3为频率作为单因素变量时压实黄土的动强度变化曲线,并绘制累积塑性应变和动强度参数变化曲线如图4和图5所示。

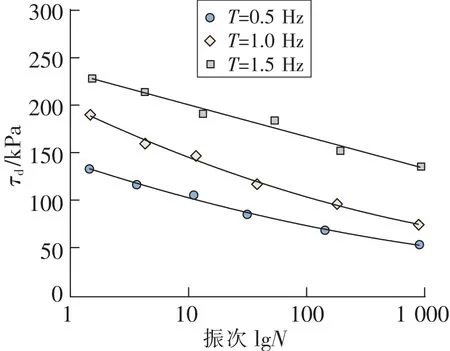
图3 不同频率下压实黄土的动强度变化规律Fig.3 Variation law of dynamic strength of compacted loess under different frequencies

图4 不同频率下压实黄土的累积塑性应变变化规律Fig.4 Variation law of cumulative plastic strain of compacted loess under different frequencies

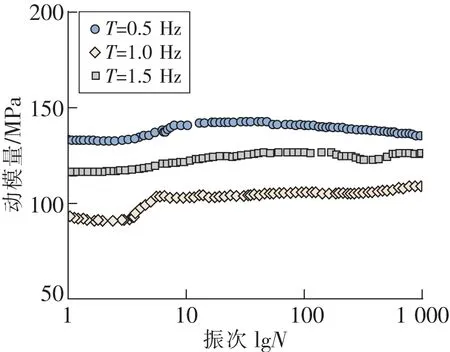
图5 不同频率下压实黄土的动模量变化规律Fig.5 Variation law of dynamic modulus of compacted loess under different frequencies

图3显示随着加载频率T的增大,抗剪强度呈现明显的减小趋势,相对于低频加载,高频荷载作用时土体孔隙水难以及时消散,此时黄土的总应力σ更大,且土体在高频荷载条件下应力作用时间短,相对于最初土体的稳定状态,内部结构并未被完全破坏,残余的颗粒咬合强度更高,因此,加载频率T=1.5 Hz时土体的动强度更高。图4和图5显示黄土累积塑性应变、动强度参数的变化规律,可以看出,加载频率T=1.5 Hz的黄土试样的累积塑性应变高于T=1.0 Hz,认为加载频率较高时,受荷载的循环作用影响,压实黄土可恢复变形受到限制,每一级施加的荷载均存在未恢复的变形。

压实黄土处于最大干密度及最优含水率状态下,高频荷载作用下黄土试样存在未恢复的累积变形,呈现出累积塑性变形更大的现象,而低频荷载作用时更容易因动剪切强度不足而出现局部破坏。考虑到加载频率与行车速度的相关性,认为车辆行驶速度在60～80 km/h时黄土路基稳定性及耐久性更佳。

2.2 不同压实度和含水率下压实黄土累积塑性变形

分析含水率和压实度对压实黄土的动力性能的影响,绘制压实黄土试样动强度、累积塑性应变以及动强度参数变化曲线如图6～8所示。

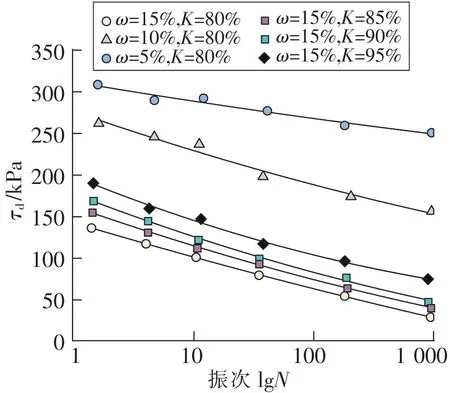
图6 不同压实度和含水率条件下压实黄土的动强度变化规律Fig.6 Variation law of dynamic strength of compacted loess under different conditions of compaction and water content

从图6可以看出,相同循环振次条件下,土体的含水率ω越高、压实度K越低,相应的动强度越低。黄土作为高水敏性的材料,含水率ω对土体内部结构影响显著,ω越高黄土内部颗粒的胶接力弱化。而压实度K决定了土体结构的密实程度,增大黄土的压实度K可以提高颗粒连接力,孔隙数量也更少,黄土试样的压实度K越高,其宏观动强度性能得到显著提升。图7为压实黄土动强度的累积塑性应变变化曲线,显而易见,动应变与动强度的变化趋势一致,土体含水率ω的增大引起了累积塑性应变提高,此外含水率ω与压实度K对黄土累积塑性应变的影响程度存在差异性,相同条件下,含水率ω引起黄土试样的累积塑性应变的最大增幅达到4.5%,而压实度K引起黄土试样的累积塑性应变的波动幅度小于1%。通过分析图8所示动强度参数变化规律,不同含水率的黄土试样动模量最大变幅为84 MPa,而不同压实度的黄土试样动模量变化幅度低于25 MPa,表明含水率对动强度参数的影响程度更显著。

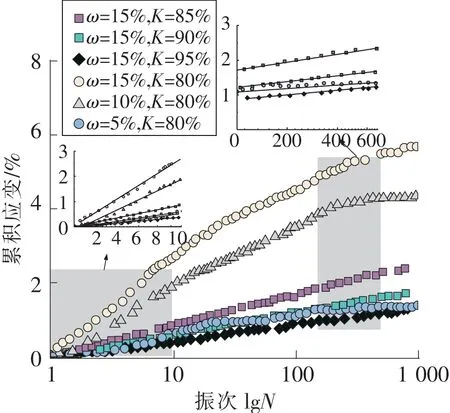
图7 不同压实度和含水率条件下压实黄土的累积塑性应变变化规律Fig.7 Variation law of cumulative plastic strain of compacted loess under different compaction and water content conditions

图8 不同压实度和含水率条件下压实黄土的动模量变化规律Fig.8 Variation law of dynamic modulus of compacted loess under different conditions of compaction and water content

综合判断,黄土对水的敏感性高,因此,含水率过高将引起黄土动强度严重的劣化,且高含水率状态土体的累积塑性变形也更高,黄土路基对水分侵入引起的动力学性能劣化显著,需要将黄土的含水率控制在合理范围内。提高压实度能够减小土体内孔隙的数量,内部结构更加稳定,挤密作用能够提高黄土的动力学性能。

2.3 孔隙水压力与能量耗散的关系

2.3.1 循环应力比的影响

图9显示均等固结Kc=1.0时的循环应力比影响下黄土的塑性应变累积能量耗散曲线,随着CSR的增加,孔隙水压力在初始骤增阶段的增加量和增加速率均降低,最终稳定孔隙水压力数值也越小,表现为曲线形态存在差异化,当CSR<0.35时,各曲线的整体趋势接近“S”型;但当CSR=0.35时,曲线的整体趋势转变为“J”型趋势,土体孔隙水压力的增长与塑性应变累积能量耗散更符合线性增加趋势。

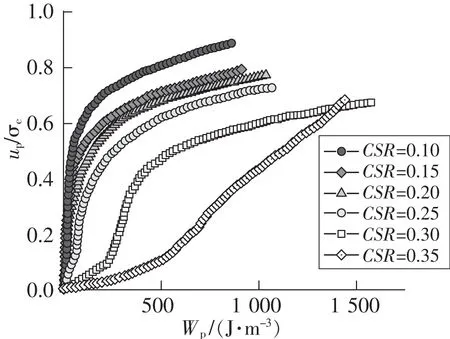
图9 循环应力比影响下黄土的塑性应变累积能量耗散曲线Fig.9 Curves of Plastic strain cumulative energy dissipation in loess under the influence of cyclic stress ratios

图10显示了均等固结Kc=1.0,不同循环应力比CSR下土体孔隙水压力比与黏滞累积能量耗散的关系曲线。由图可见,在各级循环应力比下,土体孔隙水压力随着黏滞累积能量耗散的增加显著增大,而且随着循环应力比的增加,试验初始阶段土体孔隙水压力的增加量和增速更大,但最终孔隙水压力数值稍有降低,黏滞累积能量耗散量也降低。分阶段考虑,当CSR≥0.20时,整个循环加载期间,土体累积孔隙水压力稍有降低,而黏滞累积能量明显衰减。可见,均等固结下,CSR≤0.15,试验结束时随着累积孔隙水压值的减小,土体的累积能量耗散也更小;而当循环应力比超过0.20后,认为循环应力比的波动基本不会影响土体孔隙水压和累积能量耗散二者的演化关系。

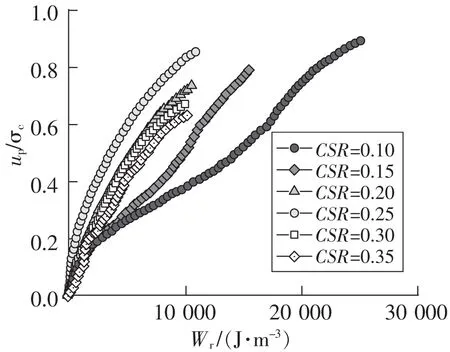
图10 循环应力比影响下黄土的黏滞累积能量耗散曲线Fig.10 Curves of cohesive cumulative energy dissipation in loess under the influence of cyclic stress ratios

归一化曲线如图11所示,定义黄土试样的累积孔隙水压达到峰值时试样破坏,通过采集土体破坏对应的黏滞能量耗散值Wrf、塑性应变能量耗散值Wpf,将统计的数据值绘制成曲线,即得到归一化关系曲线。从图11可以看出,循环应力比处于低值时,曲线斜率更大,土体的黏滞能量耗散的增长速度更快;而随着循环应力比CSR的增大,呈现出土体的塑性应变增速加快的趋势;当CSR=0.35时,出现土体塑性应变能量耗散速度更高的现象。试验数据表明,循环应力比CSR越大,压实黄土更容易出现破坏。

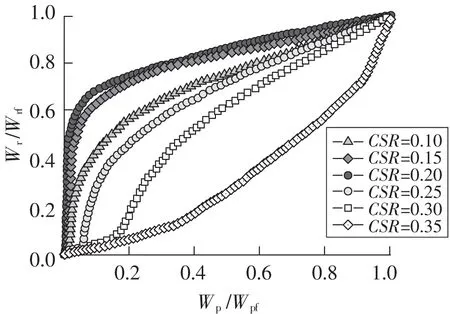
图11 循环应力比影响下归一化分析曲线Fig.11 Curves of normalised analysis under the influence of cyclic stress ratios

2.3.2 固结应力比的影响

图12描述了固结应力比的差异性对黄土的塑性应变累积能量耗散的影响规律。从图12可以看出,随着塑性应变能量耗散的增大,黄土的孔隙水压呈上升趋势。固结应力比的影响在于改变了曲线的变化形式,在固结应力比Kc≤1.4时,曲线具有明显的拐点,且发展模式有显著的阶段性变化特征。在未达到拐点前,发现土体的塑性应变能量耗散值位于(0,1 000)区间范围内,较低的能量耗散值对应较高的孔隙水压值;曲线达到拐点后,土体的塑性应变能量出现了快速增大。而当固结应力比Kc≥1.6时,曲线更为平滑,土体的塑性应变能量耗散变化更加稳定,孔隙水压也均匀增长,固结应力比越大,二者的协同关系越好。

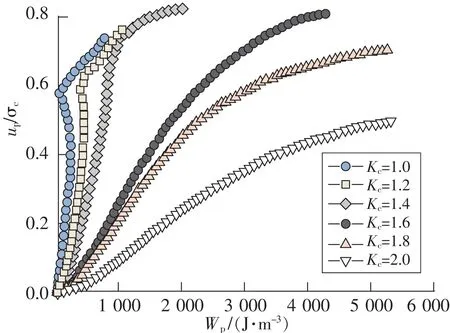
图12 固结应力比影响下黄土的塑性应变累积能量耗散曲线Fig.12 Curves of plastic strain cumulative energy dissipation in loess under the influence of consolidation stress ratio

压实黄土黏滞累积能量耗散相关曲线如图13所示。从图13可以看出,各级固结应力比下,土体孔隙水压力与黏滞累积能量耗散的关系曲线呈协同上升趋势,且无明显拐点。固结应力比Kc≤1.4时,土体发生较低的黏滞累积能量耗散就能实现较高的孔隙水压力提升,而当Kc=1.6与Kc=1.8时,曲线在加载前半程基本重合,但在加载后期,固结应力比Kc=1.6时,土体黏滞累积能量耗散越多,孔隙水压力的提升越显著。当Kc≥1.8时,土体的孔隙水压终值随着固结应力比Kc的增大而降低,而黏滞累积能量耗散值更大。原因为固结应力比越大,压实黄土的土颗粒排列更加紧密,相对位移减少,对应的能量消耗更少,且随着固结应力比的增大,压实黄土的塑性变形发展速度明显增加,因此,对应的累积塑性应变累积能量耗散的线性特性更显著。

图13 固结应力比影响下黄土的黏滞累积能量耗散曲线Fig.13 Curves of cohesive cumulative energy dissipation in loess under the influence of consolidation stress ratio

固结应力比影响下归一化关系如图14所示。可以发现,曲线的形态存在明显的差异性。当Kc≤1.2时,土体塑性应变累积能量耗散和黏滞累积能量耗散的归一化关系曲线存在明显拐点,致使曲线呈“S”型;当Kc≥1.4时,土体塑性应变累积能量耗散和黏滞累积能量耗散的归一化关系曲线拐点逐渐消失,且随着Kc的增加逐渐由轻微“S”型的曲线向直线逼近。

2.4 孔隙水压力与能量耗散的关系

循环应力比与固结应力比对土体孔隙水压-累积能量耗散二者的关系存在影响。此外,试验条件不同时,2个因素对土体孔隙水压的影响程度差异性显著。对于循环应力比影响下,S1、S2、S3、S4试验组土体孔隙水压力的增长受到黏滞累积能量的控制;而对于固结应力比影响下,S5、S8、S9、S10以及S11试验组的孔隙水压取决于塑性能量耗散和黏滞能量耗散的累积值,对于S6和S7试验组,其孔隙水压力与塑性应变累积能量耗散之间的发展关系表明二者均属于崩塌式破坏,实测结果与基于能量法的孔隙水压力增长规律差异较大。

基于含水率对黄土影响程度更大,图15为不同含水率状态的能量耗散变化情况,含水率越高入射能量越大,认为黄土试样内部裂隙的发育、颗粒的破碎等损伤均导致能量耗散,高含水率状态的黄土试样表现出更大的能量耗散率,也说明了动载作用下高含水率试样的内部损伤效应更显著。通过能量耗散原理表明,有必要控制工程中超静孔隙水压力过大导致的黄土路基劣化。

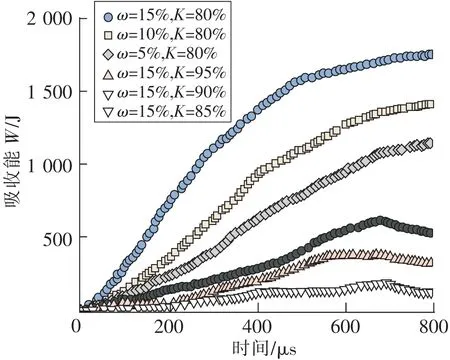
图15 不同压实度和含水率条件下压实黄土的吸收能变化规律Fig.15 Variation law of absorption energy of compacted loess under different compaction and water content conditions

对孔隙水压力与能量耗散的归一化分析,能尽可能地避免其他因素对量纲本身的影响。试样破坏时的孔隙水压力均低于围压,因此不涉及液化现象,其次对孔压和能量进行无量纲处理时以孔压最大点为破坏点,以实现对孔压和能量的无量纲处理保持对应。一般而言,循环动载作用下,压实黄土孔隙水压力的曲线发展形态可以归纳为以下3类[26-28]。

(6)

式中uf为土样破坏时的孔隙水压力,kPa;Wf为土体累积能量耗散,kJ;a为无量纲参数。

S1和S2试验组的孔隙水压力与能量耗散归一化曲线为B型,其余试验组均为A型。据此运用A型和B型孔隙水压力发展曲线进行非线性回归分析,回归参数见表3,拟合分析如图16所示。

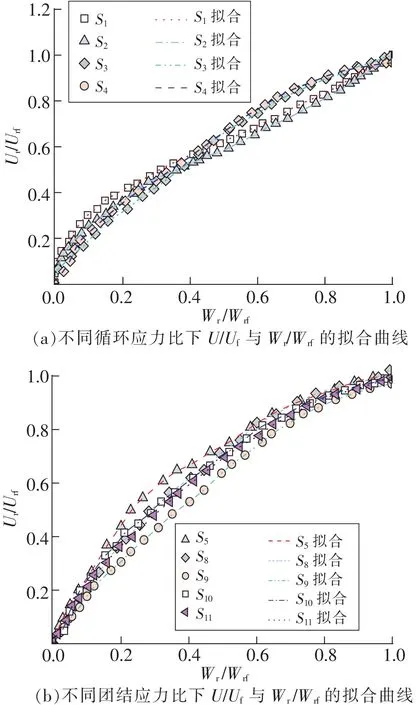
图16 黄土孔隙水压的拟合分析Fig.16 Fitting analysis of pore water pressure in loess

表3 拟合模型结果统计

目前常用的孔压模型,函数形式主要有幂函数和多项式,分析表3和图16可得,模型参数a与固结应力比Kc无明显相关性,但与循环应力比CSR具有明显相关性[29-30]。对于A型,相关关系式为:a=2.04+12.51CSR;对于B型,相关关系式为:a=-0.68+8.94CSR。

通过研究土体孔隙水压力与塑性应变累积能量耗散和黏滞累积能量耗散之间的关系,探讨了循环应力比和固结应力比两种因素对压实黄土的孔隙水压力与能量耗散关系影响规律,并基于试验数据进行回归分析,提出了黄土孔隙水压力的数学拟合计算模型,从本质上解释了压实黄土在循环动载下孔隙水压力提升的潜在机制。

3 结 论

1)路基压实黄土存在临界频率,处于临界频率附近时土体的动力学性能更好。高含水率状态土体的动强度严重劣化,提高压实度可显著提升动强度。不排水条件下,饱和压实黄土孔隙水压力动力反应与累积塑性能量耗散关系密切。均等固结下,循环应力比CSR在0.10～0.35范围内存在导致土体孔隙水压力增长模式改变的临界值。CSR≤0.15,孔隙水压力更受控于黏滞累积能量耗散;而CSR≥0.20,总累积能量耗散的影响更显著。

2)相同循环应力比下,固结应力比Kc在1.0～2.0范围内存在导致土体孔隙水压力增长模式改变的临界值。Kc=1.6时,孔隙水压力的提升与土体黏滞累积能量耗散具有正相关关系;而Kc≥1.8时,随着固结应力比的增大,压实黄土孔隙水压的最终值减小,且其黏滞累积能量耗散更大。

3)不同固结应力比引起压实黄土的塑性应变累积能量耗散和黏滞累积能量归一化的曲线形态均表现出差异化的特征。Kc≤1.2时,土体塑性应变累积能量耗散和黏滞累积能量耗散的归一化关系曲线存在明显拐点,且呈轻微“S”型;当Kc≥1.4时,土体塑性应变累积能量耗散和黏滞累积能量耗散的归一化曲线拐点逐渐消失,由轻微“S”型的曲线向直线逼近。

4)高含水率状态的黄土试样表现出更大的能量耗散率,通过能量耗散原理表明,有必要控制工程中超静孔隙水压力过大导致的黄土路基劣化。基于建立的压实黄土孔隙水压拟合模型,通过影响因素的数学相关性分析表明,拟合参数指标与固结应力比无明显相关性,但与循环应力比均存在线性关系。

5)通过研究循环动载条件下压实黄土的动力特性,掌握压实黄土路基动力变形、孔隙水压变化等规律,可为黄土路基工程的不均匀沉降变形、局部失稳等病害防治提供有益的试验支撑。