新型框架-调频减震墙抗震性能研究

张无为， 陈 鑫

（苏州科技大学 土木工程学院，江苏 苏州 215011）

结构振动控制有利于降低结构在地震、海浪、风、车辆动力等作用下所造成的损伤，能够有效地增强结构抗震防灾能力，振动控制有助于提高建筑物、桥梁的使用寿命。 近年来结构响应控制装置越来越多地应用于建筑结构中，其中消能减震装置、隔震装置、调频质量阻尼器等均有广泛应用。

一方面，调频质量阻尼器（Tuned Mass Damper，TMD）是结构振动控制的优选方案之一。 其通常设置在结构中，与主结构同步运动来调频，减轻主结构的动力反应。TMD 在大跨、高耸结构中得到了广泛应用，以减轻风和地震等自然灾害的影响（见图1），例如加拿大多伦多CN 塔、美国纽约花旗公司、中国台北101 大厦和英国伦敦千禧桥等[1]。

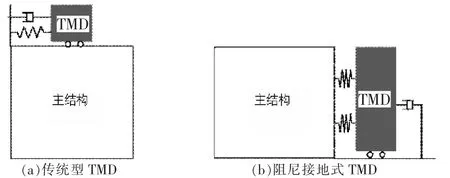
图1 调频质量阻尼器

图1（a）是传统型TMD 的力学模型，图1（b）是阻尼接地式调频质量阻尼器（Damping Grounded Tuned Mass Damper，DGTMD）的力学模型。 Ren[2]研究了阻尼接地式TMD，与普通TMD 的区别是阻尼元件不是连接到要控制的结构，而是连接到大地。 在给定相同质量比时，阻尼接地式TMD 可以比传统型TMD 更好地抑制主结构的振动。 Liu[3-4]也对传统的TMD 进行了优化，提出了挂顶式和接地式两种优化方式并对接地式TMD进行数值验算，得到最优调频参数的解析解。Cheung 和Wong[5-6]提出了一种优化方法，证明了接地型TMD 比传统TMD 和单独的阻尼器有更好的共振振幅抑制。Xiang[7-9]等提出了主结构有阻尼DGTMD 的优化方法，研究了阻尼接地型TMD 在建筑抗震方面的应用并做了小型振动台试验来验证减震效果。

另一方面，由于地震力的复杂性和强大破坏性，不同种类的减震墙被广泛用于建筑抗震中。 减震墙在地震响应下能够减轻主结构动力响应、耗散地震能量，使用减震墙可以避免墙体与框架相互作用对主要结构构件的负面影响，整个结构的抗震性能可以得到相应的提高。

减震墙包括各种耗能墙和摇摆墙。 周颖等[10]探讨了如何在高层结构中设计使用黏滞阻尼墙来达到耗能减震的目的，郭永伟和张利军[11]也模拟出在框架结构中设置黏滞阻尼墙有显著的减震效果。Yang 等[12]结合波纹钢板和软钢阻尼器，提出了阻尼耗能波纹钢板墙。Preti 等[13]通过设置砌体填充墙砌块之间的水平滑动填充层、墙与框架之间的柔性连接来减轻墙和框架之间的相互作用，进而确保结构延性和地震下的能量耗散。 董金芝等[14]提出了一种框架-预应力摇摆墙结构形式，墙体通过预应力筋与基础连接，墙与框架通过耗能元件连接，墙脚装上橡胶块。 承载能力和耗能能力显著增加，且损伤构件易于更换。

因此，课题组用TMD 和减震墙这两个元素，设计了一种新型调频减震墙。 本文重点研究框架-调频减震墙体系的抗震性能，进行了系统的精细化数值分析，评估了多遇、罕遇地震作用下新型减震墙的减震效果。

1 DGTMD 动力性能简介

1.1 动力方程

阻尼接地型调频质量阻尼器的单自由度体系动力学模型如图2 所示， 设两种模型主结构的质量均为m1，刚度均为k1，位移均为x1；子结构的质量均为m2，刚度均为k2，阻尼均为c，位移均为x2；以各自模型的静平衡位置为初始点。 根据图2，由达朗贝尔原理[3]可得到系统的动力方程

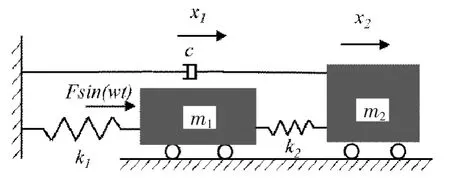
图2 SDOF-DGTMD 动力学模型

1.2 最优参数

对于主结构无阻尼的DGTMD 体系，可以基于固定点理论对简谐激励下的结构响应进行优化。 Ren 根据式（2）绘制了DGTMD 主结构频响函数曲线[2]，然后使两固定点处纵坐标等值，解出使两个固定点坐标相等时的频率比为最优频率比；根据固定点理论可知，无论阻尼比怎么取，曲线都会经过这两个定点，令两个固定点的纵坐标相等且为幅频响应曲线的最大值时，代入此时固定点的横坐标，得到ζa2和ζb2的解析式，取ζa2、ζb2的平均值ζopt2，解出最优阻尼比ζopt。 通过上述方法得出DGTMD 体系的最优频率比、阻尼比公式为

对于主结构有阻尼的DGTMD 体系， 用基于固定点理论的等效替代法进行优化。 下式为主结构有阻尼时DGTMD 最优频率比、阻尼比[15]

2 框架-调频减震墙体系建模方法

2.1 框架-调频减震墙

基于接地式调频质量阻尼器的理念，提出了框架结构-新型调频减震墙体系。 如图3 所示，其中主结构为普通框架结构，框架与钢板墙通过弹簧和分布滑动支撑连接。 钢板墙提供足够的刚度，其重量通过分布滑动支撑、上连接节点和底部连接节点共同承担，并且上连接节点和底部连接节点限制了钢板墙倾覆，使其只能水平滑动。 弹簧作为刚度单元，底部连接节点的阻尼器作为阻尼单元，与钢板墙共同组成了一个阻尼接地式TMD。 当建筑结构受到风、地震等作用，由于调频共振的原理，钢板墙发生反向振动，部分振动能量被传递到调频减震墙中的阻尼器，消耗了能量，减小了结构的振动响应。

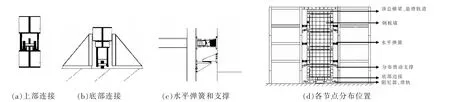
图3 阻尼接地型装配式调频减震墙

该体系包含框架结构体系和调频质量阻尼器体系，调频质量阻尼器体系包括充当主体的钢板组合墙和刚度体系、阻尼体系。 其中上连接节点、水平弹簧、分布滑动支撑、底部连接节点见图3（d）。

如图3（a）所示，顶部悬吊滑轮可以沿着悬吊轨道滚动。如图3（b）所示，钢板墙的底部与地面通过轮轴与阻尼器系统连接，在地面滚动。 阻尼器两端则分别与接轮钢板和固定于地面的节点铰接。 如图3（c）所示，水平弹簧和分布滑动支撑组成了调频减震墙的侧向连接系统。 减震墙与弹簧、阻尼器等单元共同组成了调频减震墙的质量、刚度、阻尼单元，并且通过限制使整体水平滑动达成调谐减震，当主体框架受到地震作用，钢板墙发生与主体框架运动方向相反的往复振动，部分振动能量被传递到调频减震墙中的阻尼器，消耗了传递过来的振动能量，从而减小结构振动响应。

2.2 工程算例

如图4（a）所示，江都区实验小学建乐校区教学楼，位于扬州市江都区仙女镇乐和路1 号，建于2006 年，钢筋混凝土框架结构，主体三层，局部四层突出屋面，建筑总高度13.75 m。 该建筑原为丙类建筑，结构的安全等级和耐火等级均为二级， 设计地震分组为第一组， 抗震设防烈度7度，设计基本加速度0.15g。 框架抗震等级三级，建筑场地类别为Ⅲ类，场地特征周期为0.55 s，结构的阻尼比为0.05，多遇水平地震影响系数最大值0.12。结构平面布置如图4（b）所示，结构平面设有抗震缝，分析时可将结构分割为4 个单体进行分析，本文选取其中单体B 区中D 轴的典型结构进行建模。 该区域结构首层层高为4.2 m，第二、三层层高均为3.6 m。结构横向两跨，跨度分别为3.0 m 和7.5 m，为典型的教室、阳台两跨RC框架校舍结构。

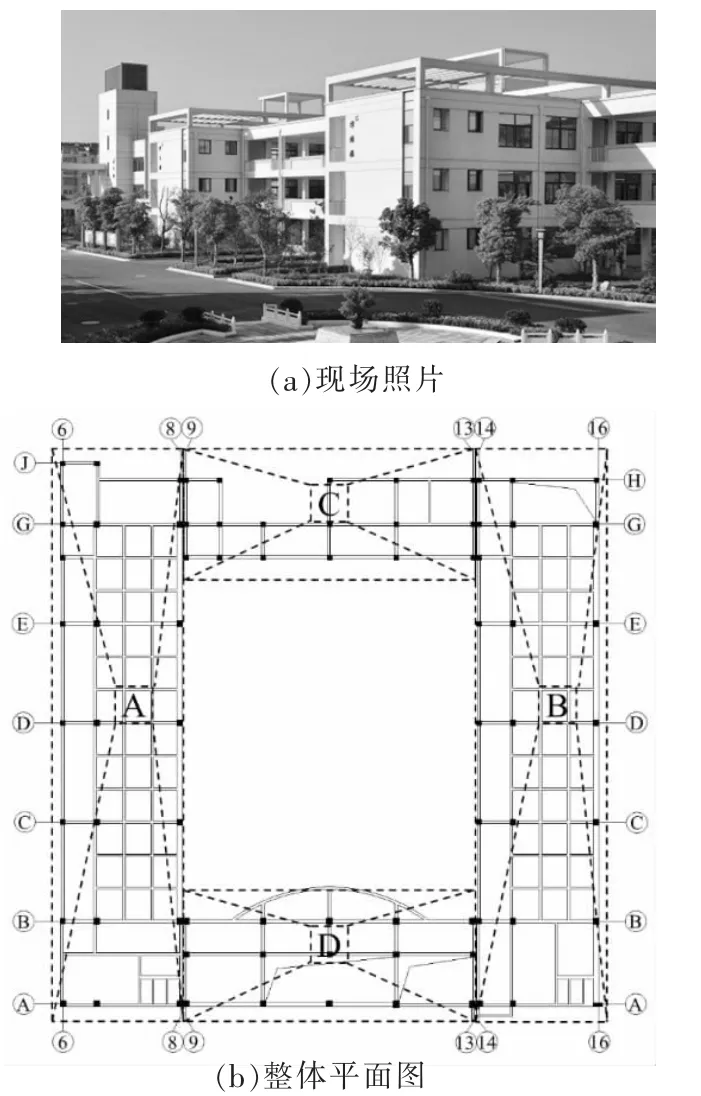
图4 某小学教学主楼抗震分区

主体校舍的梁、 柱结构混凝土均使用C30 规格， 梁板采用HRB335钢筋，柱采用HRB400 钢筋。 平面梁柱布置如图5 所示，截面尺寸如表1所示。 结构质量为1 824 t，本节通过设置调频减震墙的方式对结构进行加固，以探究调频减震墙的减震效果。

表1 梁柱截面尺寸 mm

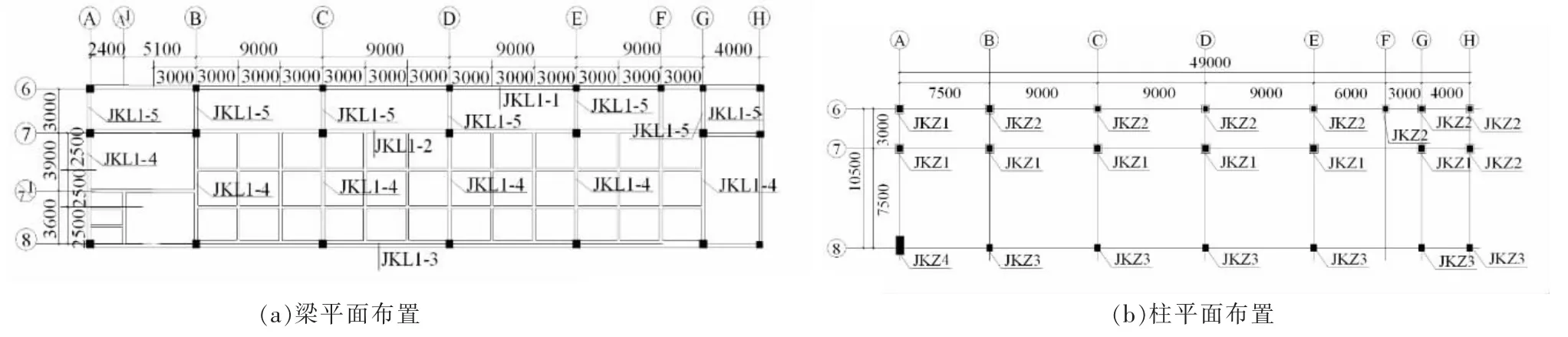
图5 框架结构平面图

2.3 有限元模型建立

框架部分采用Opensees 直接建模， 需要考虑混凝土本构和钢筋本构的选取。 混凝土单元选用Concrete02 和Concrete04 本构模型， 其中Concrete02 单元考虑了混凝土受拉受压性能还有开裂后的刚度退化，Concrete04 单元是在考虑混凝土约束效应的基础上进行卸载和加载的本构模型。因此，非约束区混凝土采用Concrete02 本构模型，约束区混凝土采用Concrete04 本构模型[17]。 钢筋采用Steel 01 本构，如图6（c）所示，fy为钢筋屈服强度，E0为钢筋弹性模量，b 为硬化系数。 多遇地震作用下，梁和柱均采用Elastic BeamColumn 单元，罕遇地震作用下采用基于刚度的Disp BeamColumn 单元。后者是基于刚度的纤维单元，纤维模型将梁、柱构件划分为一系列平行于轴线的纤维单元，根据实截面特性选取合适的材料进行有限元分析，可以真实反映各种材料的特性，计算结果能够真实反应结构的受力特性[18]。

图6 不同的本构模型

在对梁柱的非线性分析中，通常采用这种纤维单元。 在Opensees 中，调频减震墙的建模包括钢板、连接节点、 弹簧、 阻尼器。 钢板墙顶部、 底部连接约束自由度使其平动， 钢板采用ShellMITC4 单元进行模拟。ShellMITC4 单元采用结合了修正剪力场插值的双线性等参列式来提高薄板的弯曲性能，采用弹性材料则属于弹性壳体单元。 框架与调频减震墙连接的弹簧使用Truss 单元进行模拟，底部阻尼器使用ViscousDamper本构进行模拟，用Two node link 单元将阻尼器与框架连接。 梁、柱截面的纤维分布如图7 所示。

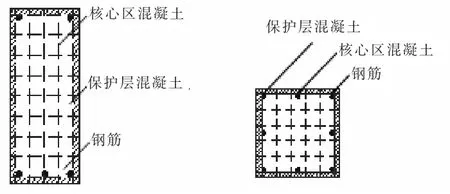
图7 截面纤维（左：梁截面；右：柱截面）

为了具体比较框架结构在地震作用下的抗震性能和附加调频减震墙后的性能， 分别用PKPM、Etabs、Opensees 等软件对结构进行模态分析，得到框架结构的基本周期为0.661 s，其他软件模态如表2 所示。 对应的振型如图8 所示，结构1 阶振型为横向平动，2 阶振型为纵向平动，3 阶振型为扭转，呈现典型的多层框架自振特性。 采用不同软件所建立模型得到的结构前3 阶自振周期较为接近，1 阶周期相差较小，动力特性相近，模型具有较高的可靠性，可用于进一步的结构性能分析。

表2 结构自振周期

图8 前三阶振型图（a：一阶模态；b：二阶模态；c：三阶模态）

2.4 调频减震墙参数设定

实际工程中一方面钢梁、钢柱、连接件等构件也提供部分质量，并通过设置牛腿等方式提供抗侧刚度和质量属性，另一方面使用防屈曲钢板墙、钢板组合墙时还包括填充物或覆盖层质量，因此在建立分析模型时根据实际做法加以简化，有限元模型中以集中质量的形式模拟钢板的质量，尺寸大小在模拟时仅影响侧向刚度，本文选取的尺寸初始刚度较大，对结果影响较小。

既有框架结构的一阶周期为0.661 s，频率为1.51 Hz。调频减震墙的质量比取0.05，框架质量为1 824 t，调频墙地震质量为91 t，为防止结构偏心，在结构两端分别设置墙体，每个墙体质量相等，为墙体总质量的一半。 频率比和阻尼比按照1.2 节式（4）分别取为0.993、0.097，弹簧总刚度为8 121 N/mm，每个弹簧刚度为6 77 N/mm，总阻尼为168 N·s/mm，每个阻尼器阻尼为42 N·s/mm。 设计钢板墙尺寸时需考虑满足调频所需的质量和抗侧刚度。 最终设计尺寸为厚度60 mm，宽度4 600 mm。

如图9 所示，使用Opensees 软件，在原框架模型短跨平面处附加调频减震墙。在平面框架上附加刚性梁节点，在分析中视作长度较短，刚度较大的刚臂。 此连接梁两端分别连接框架和弹簧，取较大的刚度才能协同框架与调频墙。

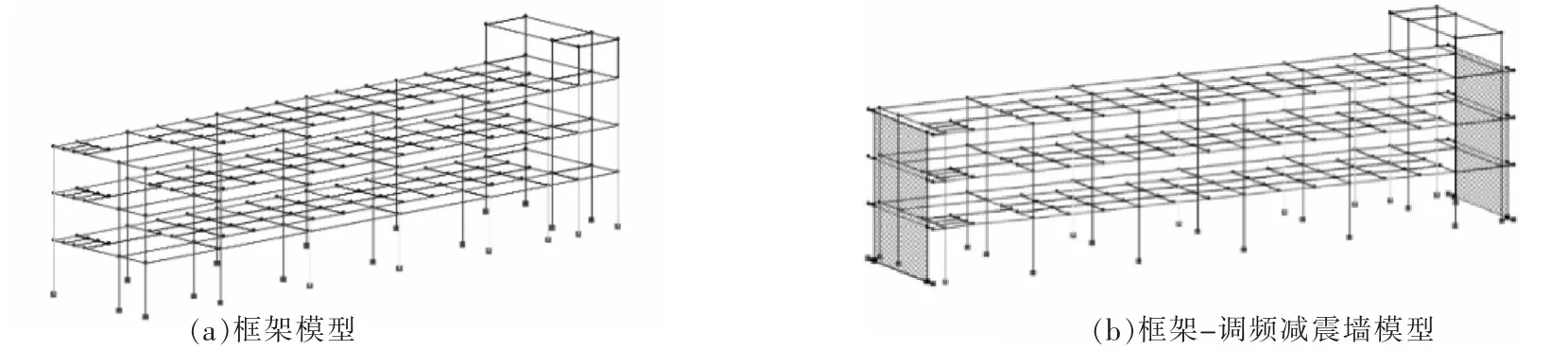
图9 加调频墙前后结构模型

3 结构动力响应分析

3.1 地震动记录选取

为模拟该工程算例在地震作用下的结构响应， 比较结构在地震作用下的位移响应并验算方案，从已有的地震动记录数据中，采取基于设计反应谱的选取方法选取三条记录进行地震响应计算（见图10），所选地震动记录的调幅后反应谱在短周期段与设计反应谱应尽可能接近。 通过图10 与规范反应谱的对比可以看出，所选取的地震波与标准反应谱曲线的频域能量在统计意义上相符。 地震动记录参数见表3 所示。

表3 地震动选取

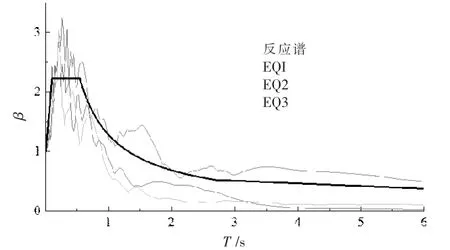
图10 地震动反应谱

3.2 多遇地震下的结构响应

结构为规则的方形框架， 短跨方向抗震性能较弱。 沿短跨平面方向输入地震动记录， 将地震动记录的PGA 调至55 gal，对结构进行多遇地震作用下的时程分析。 图11 给出了多遇地震作用下的结构层间位移角对比，从中可见：（1）加调频减震墙前、后结构层间位移角最大值均出现于2 层，2 层为结构薄弱层；（2）加调频减震墙后结构最大层间位移角降低，2 层平均层间位移角降低值为29.3%。

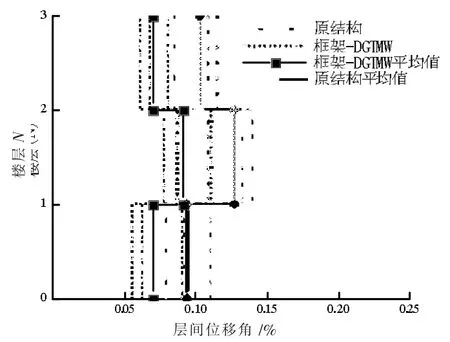
图11 多遇地震层间位移角

图12 给出了EQ1 作用下底层剪力-位移关系曲线、顶点时间-位移曲线，可见：（1）在EQ1 作用下，加调频减震墙后结构峰值位移衰减，最大峰值位移降低38.6%；（2）由于输入的地震峰值加速度较小，此时结构仍处于弹性状态，加调频减震墙后基底剪力降低，但未改变框架结构刚度；（3）从时域分析可知，加调频减震墙后结构在时程曲线多处峰值的位移值均有所降低，调频减震效果良好。

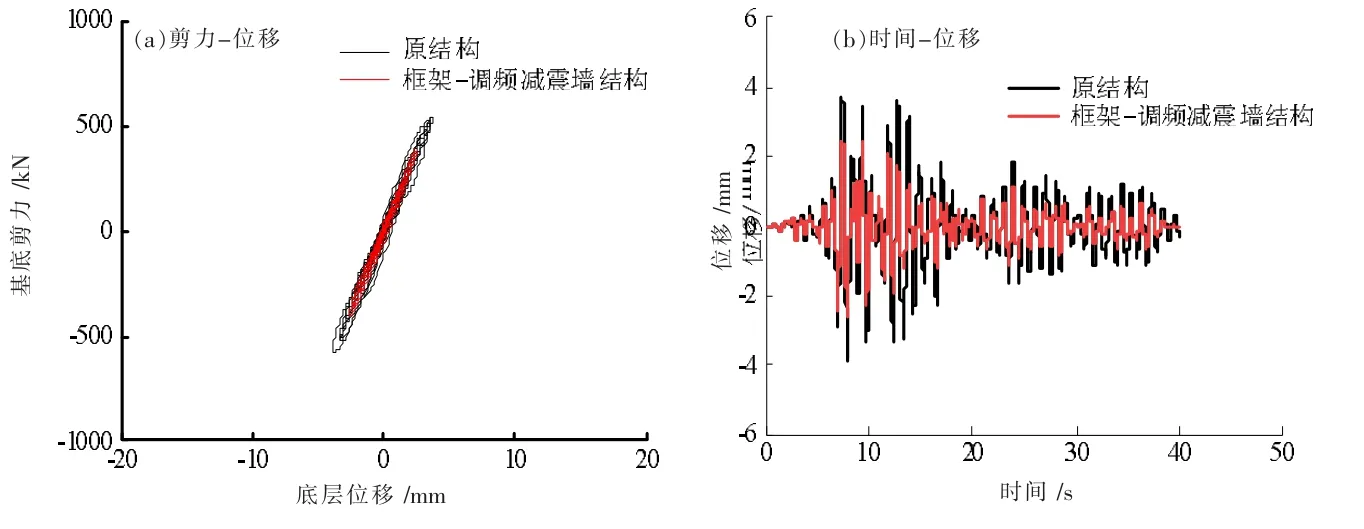
图12 多遇地震结构响应

3.3 罕遇地震下的结构响应

将地震动记录的PGA 调至310 gal，对结构进行罕遇地震作用下的弹塑性时程分析。 图13 为罕遇地震作用下的结构层间位移角对比，可见：（1）加调频减震墙前、后薄弱层与多遇地震下相同；（2）加调频减震墙后结构层间位移角降低，2 层平均层间位移角降低了22.9%；（3） 罕遇地震下调频墙减震效果弱于多遇地震下的效果；相较于多遇地震，平均减震效果降低了6.4%。

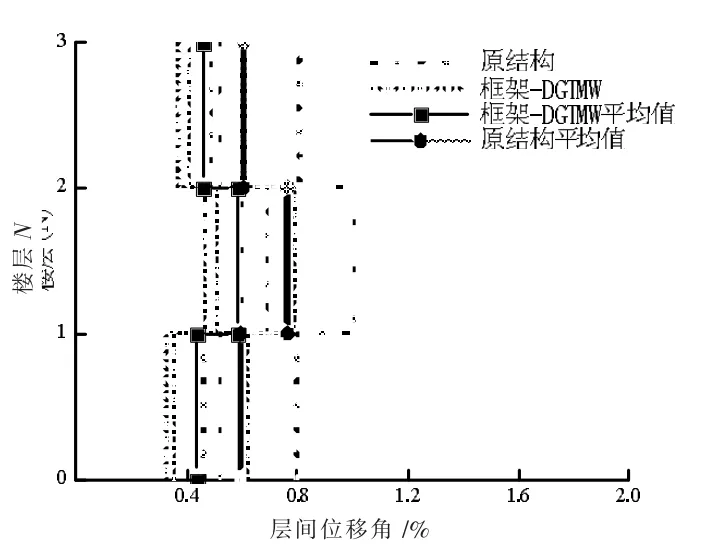
图13 罕遇地震层间位移角

图14 给出了EQ1 调幅至罕遇等级作用下底层剪力-位移关系曲线、顶点时间-位移曲线，由图可知：（1）与多遇地震作用下规律相同，加调频减震墙后结构峰值位移衰减，最大峰值位移降低20.5%；（2）大震下，结构进入弹塑性状态，加调频减震墙后的基底剪力降低，结构的损伤减小；（3）从时域分析可以看出加调频减震墙后大震下曲线多处峰值位移均有所降低，调频减震效果良好；但与多遇地震影响对比，调频减震幅度有所降低。 罕遇地震作用下，部分构件破坏，刚度降低，周期发生变化，调频减震效果受到影响。

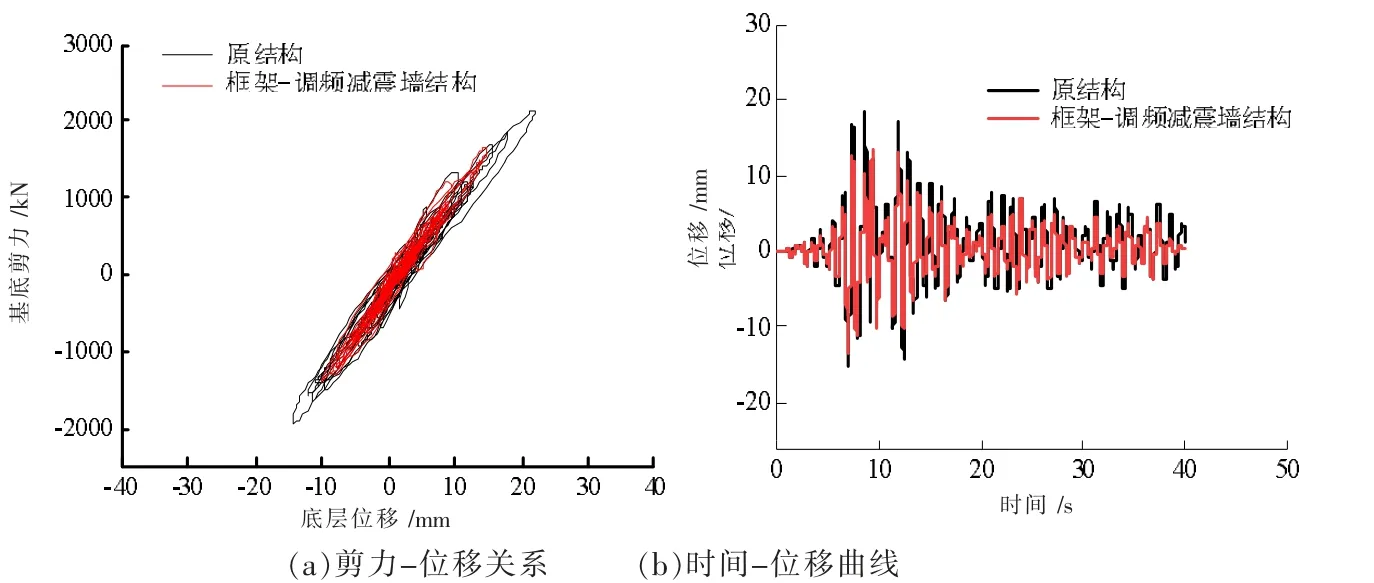
图14 罕遇地震结构响应

4 考虑弹塑性阶段的参数优化

4.1 结构退化频率

采用Morlet 小波对多自由度框架-调频减震墙结构的位移时程响应进行连续小波变换得到位移响应小波时频谱，并用不同亮度代表不同频率的幅值，首先提取EQ1 大震作用下原结构位移响应曲线，对其进行时频分析，得到小波时频图如图15 所示，图中响应最大的点位于1.099 Hz。 说明大震下结构受到损伤，主频降低。 不同色块对应不同幅值，谱幅值与小波系数相关，小波系数就是小波基函数与原信号相似的系数，色块越亮说明该时频处幅值越大，地震能量越高。

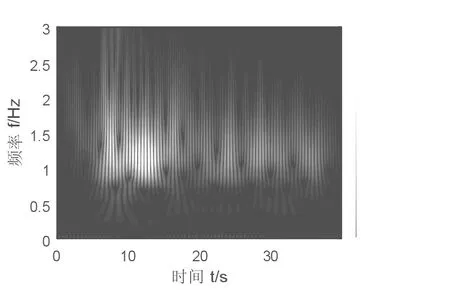
图15 罕遇地震结构时频分析

4.2 参数优化

地震作用下结构从弹性阶段过渡到弹塑性阶段，结构动力特性发生变化，针对一阶周期的调频可能在弹塑性阶段效果降低。 因此为了兼顾两阶段的减震效果，需要对设计频率进行迭代优化，具体流程如下：

（1）根据框架结构弹性特性设计调频减震墙最优频率比和阻尼比。

（2）对结构进行弹塑性动力响应分析，提取位移响应结果进行时频分析，识别由于结构损伤导致的退化后频率。

（3）取弹性阶段的最优频率f0和弹塑性阶段的退化频率f1之间的频带为最优减震频率区间，在区间内进行迭代优化计算：取退化频率f1为初始频率，确定最优参数。分别代入弹性、弹塑性阶段的结构计算框架-调频减震墙弹性减震率σ1E和弹塑性减震率σ1N。 如果取退化频率计算下σ1E也达到减震目标，则计算停止；如果σ1E未达标，取优化频率f2=（f0+f1）/2，重复上述计算步骤，得到弹性减震率σ2E和弹塑性减震率σ2N；如果σ2E与σ2N均达到理想减震率，则计算停止；若σ2E未达标，则取优化频率f3=（f0+f2）/2，若σ2N未达标，则取优化频率f3=（f1+f2）/2，重复计算步骤。 接下来迭代计算直至σnE和σnN均达标或取至满意值。

（4）根据上述数值分析结果设置优化调整减震墙设计方案。

（5）对地震作用下的框架-调频减震墙结构进行弹性、弹塑性时程分析，验算不同地震下优化后的减震效果。 若减震效果达标，则流程结束，若不达标，则重复第三步的优化设计。

考虑弹塑性阶段结构损伤来进行调频减震墙参数设计。 方案一以结构一阶频率1.512 Hz 来计算最优参数；方案二是以退化频率1.099 Hz 至结构一阶频率1.512 Hz 之间为频率优化区间，按照二分法调整最优频率进行迭代设计不断调整频率。经过迭代优化后取最优频率为1.235 Hz，通过式（4）分别计算小震下、大震下的整体结构响应，如图16 所示。 在图16 中，通过方案一，方案二和原结构的对比可以看出，无论是小震还是大震下两个方案在时域上均比原结构响应小，频域上幅值也低于原结构。 对比方案一，方案二可以得出，小震下方案一在时域、频域上的峰值均低于方案二；大震下方案二在时域、频域上的峰值均低于方案一。

图16 时域、频域结构响应对比

经过计算，方案一的最大层间角降低率为38.6%，优化后方案二降低率与之相比小了12%；大震下方案一的最大层间角降低率为20.5%，优化后方案二降低率与之相比大了5%；即用小震下减震效果的降低换来大震下减震效果的提高，并且大震下结构的残余变形方案二相比方案一降低了25%。

5 结论

（1）建立了简谐荷载作用下SDOF-DGTMD 体系动力方程，获得了DGTMD 最优设计公式。

（2）提出了新型调频减震墙装置，阐述了其构造及功能，建立了框架-调频减震墙体系有限元建模方法，并提出了分析模型。

（3）开展了框架-调频减震墙体系动力响应参数分析。 针对某数值案例，设计了调频减震墙减震方案，开展了多遇、罕遇地震作用下的结构响应分析。 结果表明，加调频减震墙后结构层间位移角均有所降低，多遇地震下薄弱层平均层间位移角降低值为29.3%；罕遇地震下薄弱层平均层间位移角降低值为22.9%。 罕遇地震作用下，部分构件破坏，刚度降低，周期发生变化，考虑弹塑性阶段结构损伤来设计调频减震墙可改善罕遇地震下减震效果。