SV 波入射下圆弧形凸起地形地震响应
孙 青, 丁海平, 张如艳
(苏州科技大学 江苏省结构工程重点实验室,江苏 苏州 215011)
凸起地形是常见的复杂地形之一,对地震波的传播有很大影响。 国内[1-3]和国外[4-7]的震后调查均发现不同山区建筑的震害存在明显差异。 强震仪也经常记录到山脊地形顶部出现的异常高峰值加速度,如1971 年圣费尔南多6.4 级地震[8],在靠近Pacoima 大坝的尖锐三角形山脊顶部的PGA 为1.25g;1994 年北岭地震[9]在Tarzana 山地的PGA 达到1.78g。 由于山区地形和构造的复杂,从强震记录中很难得到定量和规律性结果。
研究地形对地震动影响的主要方法有解析方法和数值方法,如文献[11-17]采用这些方法研究了不同入射波形式、不同波长和不同入射角等诸多因素对凸起地形放大效应的影响。 在这些研究中,凸起山脊模型多为均匀半空间[18-20],而对层状半空间凸起地形的地震响应的研究相对较少[21-23]。
本文将利用有限元软件Ansys 计算均匀半空间和层状半空间圆弧形凸起地形对入射SV 波的地震响应。 为避免采用不同的地震波入射下呈现的地表地震动峰值分布的差异[25-27],本文对频域结果进行了分析,通过对不同入射波频率、入射角度和凸起高宽比情形下凸起地形地表谱放大系数的比较,讨论均匀半空间和层状半空间圆弧形凸起地形对地震波传播影响差异。
1 计算原理
如图1 所示由人工边界和地表包围的区域结构-地基系统,运动方程为
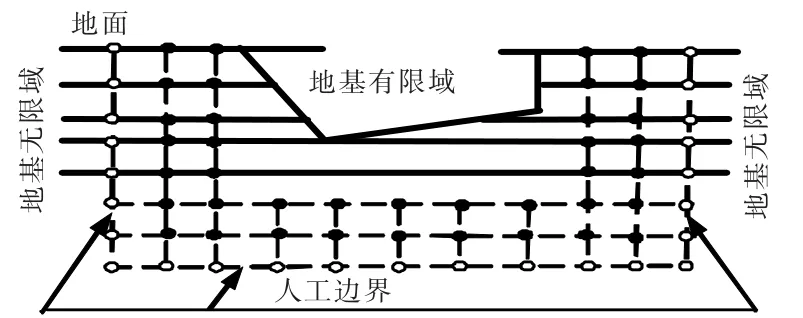
图1 结构-地基系统动力反应分析示意图
式中,M 为质量矩阵,C为阻尼矩阵,K 为刚度矩阵,P 为外力矢量。
在地震波作用下,需要解决好地基无限域界问题,本文采用的人工边界是多次透射公式(Multi-Transmitting Formula,简记为MTF)[21,24]。 基于透射人工边界原理,可得到其动力响应的计算公式
式中,N 为透射阶数(文中取2 阶);0 表示人工边界点;j 为与节点0 相邻的计算点;u0p+1为边界节点p+1 时刻的位移;ujp+1-j为p+1 时刻j 计算点的位移。
由于MTF 模拟的是外行波,即散射波us,其表达式为
式中,us散射波位移,u 为全波场位移,ur为参考波场的位移(对底边界,参考波场可直接取输入场,对侧边界,则通常取为自由场)。 令多次透射公式(2)中u0=us,0,将式(4)代入式(2)中,则
假定输入地震波为位移,则输入面为人工边界节点所在位置,人工边界点的全波场位移为
式(6)的u0p+1实际就是结构-地基系统在地震荷载作用下的边界点的位移反应,同时实现了地震波的输入。
2 输入波形与计算模型
假定模型底部入射SV 波,脉冲波采用下式的δ 函数的有限差分近似[28]
其中,G(t)=(τ)3H(τ),τ=t/T,T 为脉冲持时;H(τ)是Heaviside 函数。 波形如图2(a)所示,对应的傅里叶谱见图2(b)。
本文的计算模型分别为均匀半空间凸起圆弧山脊模型(见图3(a))和层状半空间凸起圆弧山脊模型(见图3(b))。 均匀半空间凸起圆弧形山脊(模型A)长度为400 m,高度为200 m,介质密度ρ=1 500 kg/m3,剪切波速cs=500 m/s,泊松比μ=1/3,图中a 是圆弧形凸起山脊的半宽,取a=50 m。
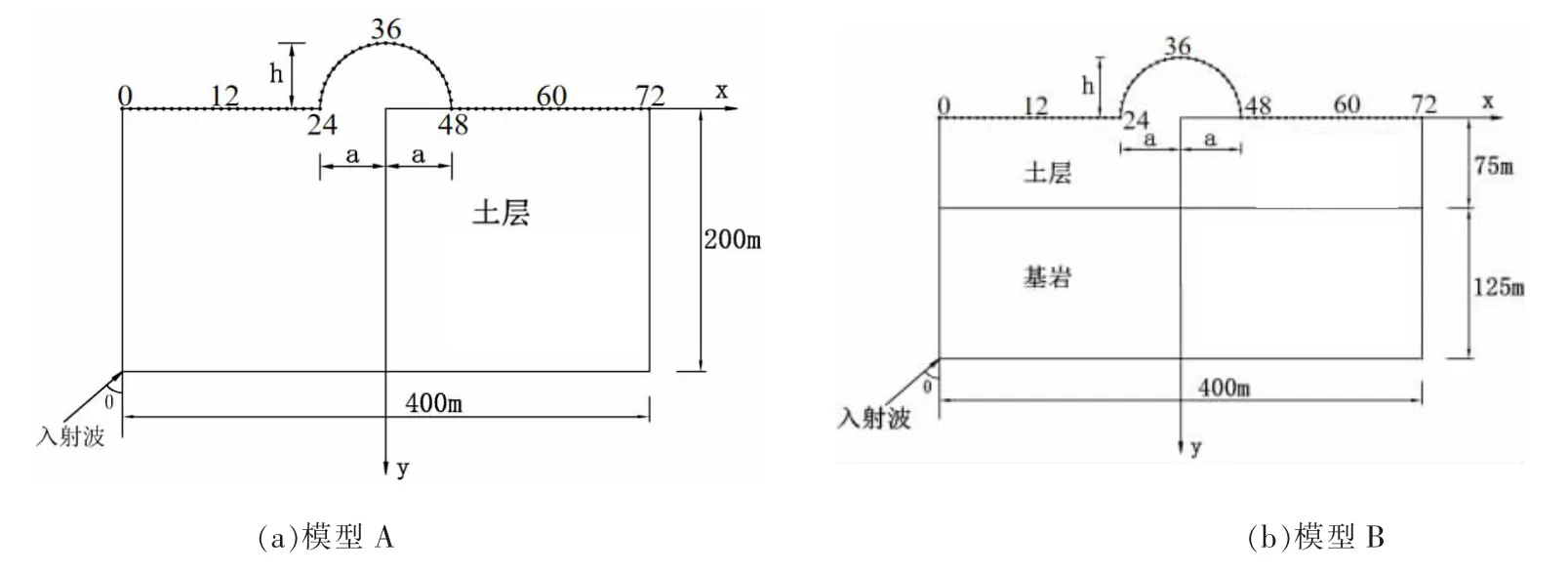
图3 计算模型示意图
层状半空间凸起圆弧山脊(模型B)长度同样为400 m,高度为200 m,其中土层高度为75 m,基岩高度为125 m。 模型中土层剪切波速cs=500 m/s、密度ρ=1 500 kg/m3,泊松比μ=1/3;基岩的剪切波速cs=800 m/s、密度ρ=2 100 kg/m3, 泊松比μ=1/3; 半圆形凸起山脊半宽a=50 m。 模型的圆弧凸起高度h 分别取a、0.75a、0.5a 和0.25a,即50 m、37.5 m、25 m 和12.5 m。
进行有限元数值模拟时,网格尺寸一般需要满足在一个有意义的波长内包含有6~10 个单元网格,取
在上述式中,λ 表示为入射波的波长,cs为土层介质中的剪切波速,fcut表示为入射波的截止频率。在网格尺寸的大小被确定后,可以按照稳定条件来确定时间步距,具体如下
式中,Cmax为入射波的最大波速。根据计算模型和介质参数,网格大小取Δx=1.25 m,时间步长Δt=0.001 25 s。
解析方法给出的场地地震响应一般是基于无量纲频率的谱比(或称谱放大系数),无量纲频率定义为
其中,a 为凸起地形半宽,λs为土层介质中剪切波波长,cs为土层剪切波速,ω 为圆频率。 无量纲频率η 由凸起地形宽度与土层介质中剪切波波长之比决定,η 值越大,其入射波波长越小,对应的频率f 越高。
由于在图2 脉冲波作用下得到的是实际频率的地震动放大效应,需要转换为无量纲频率下的结果。根据计算模型中凸起半宽与土介质特性,由式(10)可得无量纲频率与实际频率对应关系,见表1。

表1 无量纲频率对应的实际频率
为了验证本文计算方法的正确性,采用与文献[13]相同的均匀半空间凸起半圆模型作为算例(图3 模型A,h=a),计算垂直入射脉冲波(θ=0°)时的地表响应。选取上述模型地表的73 个观测点(编号为0-72)水平方向和竖直方向的位移时程,并进行傅里叶变换,再计算与入射波位移的傅里叶幅值谱的比值,得到地表各点的谱放大系数。 图4 为本文计算结果与文献[13](入射角θ=0°,无量纲频率η=1 的解析解)的比较,二者结果吻合,因此本文的计算方法是可行的。
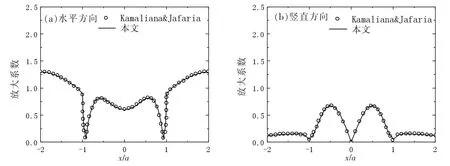
图4 本文计算结果与文献[13]结果的比较
3 圆弧形凸起地形地震响应结果与分析
3.1 频域结果分析
采用本文提出的有限元模拟方法,首先得到了SV 波分别以0°和30°入射均匀半空间圆弧形山脊(图3模型A)和层状半空间圆弧形山脊(图3 模型B)地表各个点的位移时程,并进行傅里叶变换,计算其与入射波位移的傅里叶幅值谱的比值,即谱放大系数β,图5 至图8 给出了无量纲频率分别为η=0.5、1 和2, h/a 分别为1.0、0.75、0.5 和0.25 的谱放大系数β 结果。
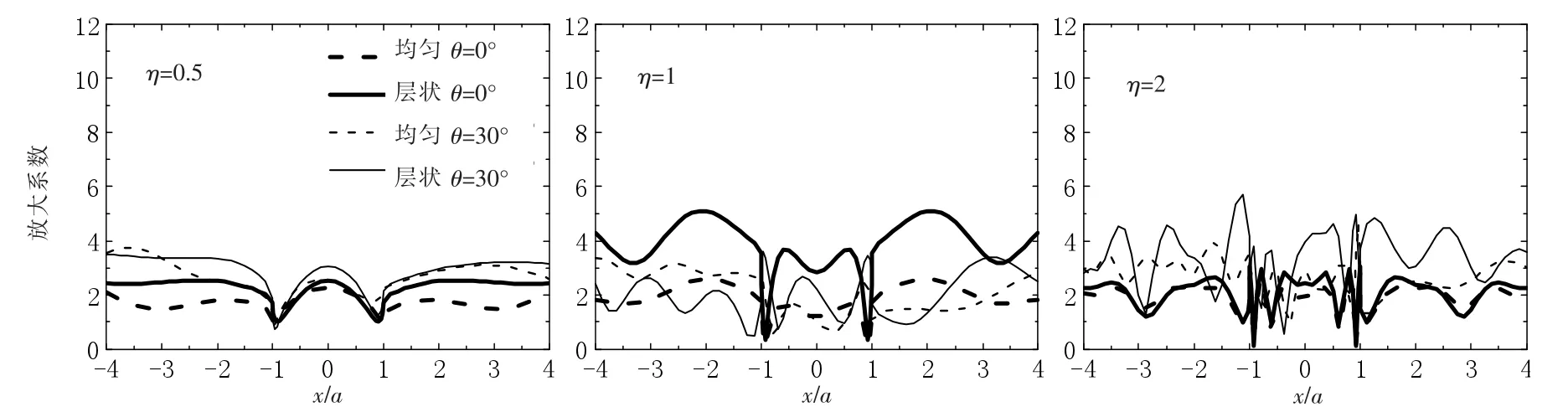
图5 不同入射角度的半圆形凸起地表位移谱放大曲线(h=50 m,h/a=1.0)
从图5 至图8 可以看出,不同无量纲频率、入射角度和凸起高宽比对圆弧形凸起地形地表位移谱放大系数β 的影响不同。 当SV 波垂直入射(θ=0°)时,由于地形的对称性,均匀半空间和层状半空间的凸起地形两侧地表的位移谱放大系数β 呈对称分布,随着无量纲频率η 和入射角度θ 的增大,地表观测点位移谱放大曲线变化更加复杂强烈,谱放大系数β 的最大值向右侧偏移,但偏移的幅度不大;在=1 时,凸起地形山脚处的谱放大系数β 比附近其它值都小,基本小于0.5;当1<<4 时,谱放大系数β 在2.0 上下波动。 图6 至图8 为模型A(h=37.5、25、12.5 m)在SV 波以不同入射角度下地表观测点的谱放大系数。 在高宽比较小(h/a=0.25),η≤1.0 的情况下, 凸起山脊对附近地震响应的放大作用较小; 而h/a=0.5,η=2,x/a=0.26时,谱放大系数β=7.53。 因此凸起地形地震危险性评价既要认真考虑高宽比,又要考虑入射波的频谱特征。
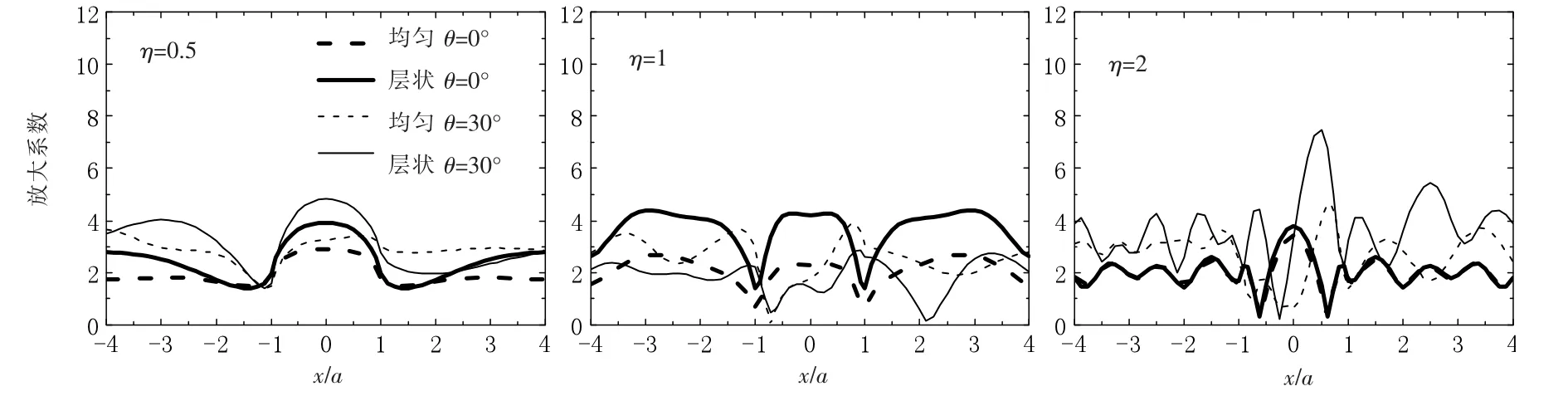
图7 不同入射角度的圆弧形凸起地表位移谱放大曲线(h=25 m,h/a=0.5)
图8 不同入射角度的圆弧形凸起地表位移谱放大曲线(h=12.5 m,h/a=0.25)
SV 波入射下层状半空间与均匀半空间圆弧形凸起地形的地表位移谱放大系数β 相比, 存在明显差异:在≤1.0 范围内, 层状半空间的地表位移谱放大系数明显大于均匀半空间的谱放大系数, 如图5 所示,当η=1,θ=0°,x/a=-2 时,均匀半空间凸起地形的β=2.59,对应层状半空间凸起地形的β=5.10,谱放大系数值增大了0.97 倍。 随着无量纲频率和入射角度的增大,两种情况的差异逐渐减小。 但在>1.0 范围内,有层状半空间的地表位移谱放大系数小于均匀半空间的谱放大系数的情形出现,如图7 所示,η=0.5,θ=30°,x/a=2 时,层状半空间的β=1.94,而对应均匀半空间的β=2.81,谱放大系数值减小了0.31 倍。
3.2 时域结果分析
采用本文提出的有限元模拟方法,首先得到了SV 波分别以0°和30°入射均匀半空间圆弧形山脊(图3模型A)和层状半空间圆弧形山脊(图3 模型B)地表各个点的时程。 图9 至图12 给出了几个特殊点即圆弧凸起的左脚点(点24)、顶点(点36)和右脚点(点48)的时程,进行比较。
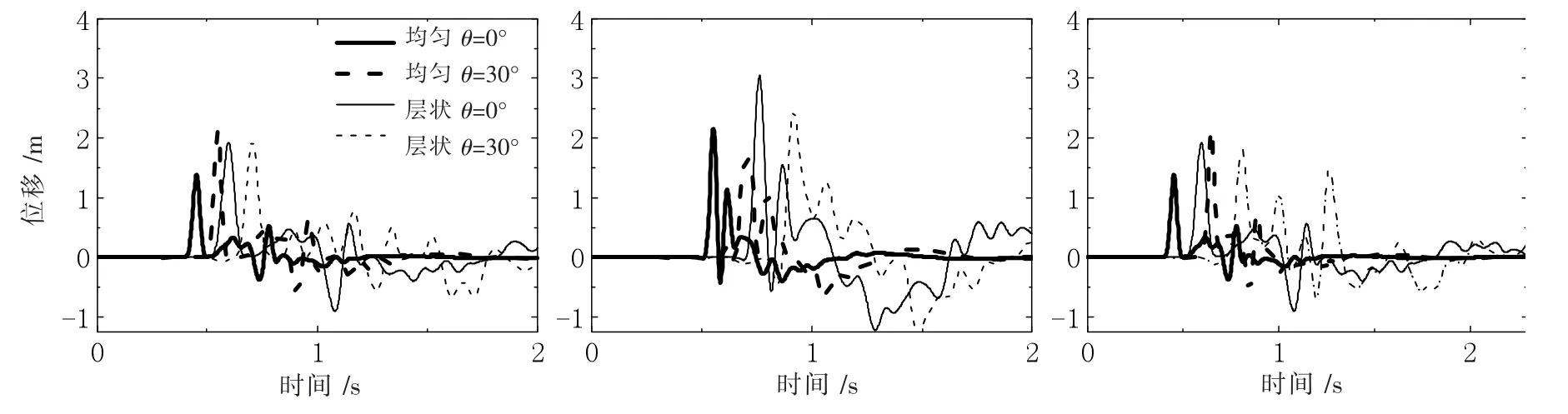
图9 圆弧高度h=50 m 的地表观测点24(左)、36(中)、48(右)时程比较

图10 圆弧高度h=37.5 m 的地表观测点24(左)、36(中)、48(右)时程比较
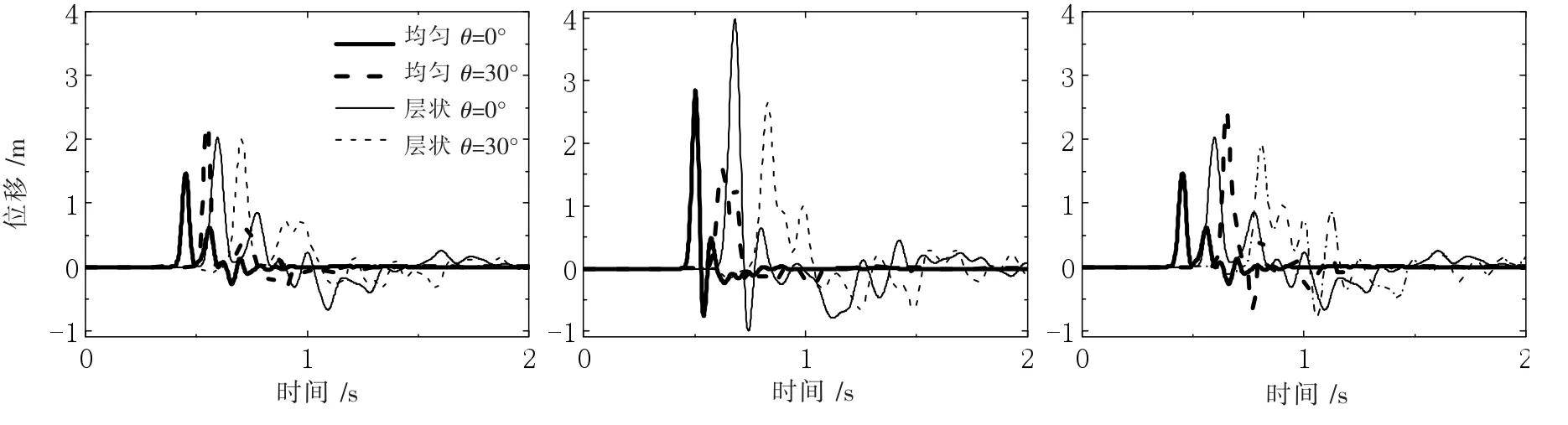
图11 圆弧高度h=25 m 的地表观测点24(左)、36(中)、48(右)时程比较
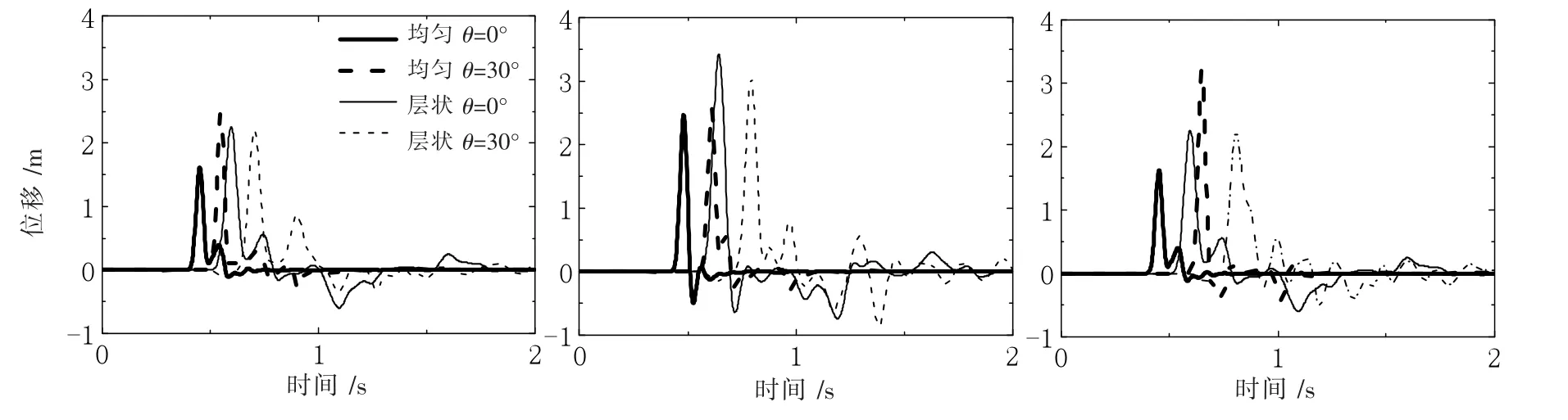
图12 圆弧高度h=12.5 m 的地表观测点24(左)、36(中)、48(右)时程比较
从图中对地表观测点24、36、48 位移时程的比较看出,同一圆弧高度的凸起地形层状半空间的地表位移峰值大于均匀半空间的地表位移的峰值,并且层状半空间内出现峰值的时间要晚于均匀半空间;地震响应持时明显延长,表明层状半空间凸起地形能增强对地震动的散射和反射效应并延长地震动持时,层状半空间凸起地形的放大效应比均匀半空间更加显著,如图9 所示,当h=50 m,x=0.55 s 时,观测点36 均匀半空间的位移峰值为2.16 m,对应层状半空间的出现位移峰值时间延迟到0.76 s,位移峰值为3.04 m,增大了40.7%左右。 因此,在进行凸起场地对地震波传播影响研究时,需要综合考虑地表地形和地下波速结构的因素。
对比这三个观测点,顶点36 的位移峰值始终大于两个脚点24、48,圆弧高度对地面运动的影响显著,在θ=0°时,两脚点24、48 的时程结果呈对称分布;当h=25 m 时,顶点在层状半空间的最大位移值为3.97 m,比圆弧高度为50 m、37.5 m、12.5 m 的凸起地形的位移峰值分别增加了23.4%、9.8%、13.6%; 当h=50 m 时,两脚点在均匀半空间的最小位移值为1.37 m,随着圆弧高度的增加,对地面运动的削弱作用更加明显,比圆弧高度为37.5 m、25 m、12.5 m 的凸起地形的位移峰值分别降低了2.8%、6.4%、15.4%, 但随着入射角度的增大,山脊右脚点48 比点24 晚出现地震响应且峰值更大,位移时程变化更复杂。
4 结论
本文采用有限元数值方法计算了均匀半空间和层状半空间圆弧形凸起山脊地形对入射SV 波的放大效应。 讨论分析了不同入射波频率、入射角度和不同的凸起高宽比等因素对均匀半空间和层状半空间圆弧形凸起山脊地形的不同影响,得到如下结论:
(1)不同的无量纲频率η、入射角度θ 和高宽比h/a 对圆弧形凸起的位移谱放大系数的影响显著,随着η、θ 和h/a 的增大,地表观测点位移谱放大系数变得复杂,因此对复杂场地进行地震危险性分析时既要认真考虑高宽比,又要考虑入射波的频谱特征。
(2)圆弧形凸起地形对于地震动的影响非常显著,圆弧形凸起地形顶点的位移放大效应显著大于两脚点的,在山顶处对地震动具有非常显著的放大作用,随着圆弧高度h 的增加,山脚处对地表地震动的削弱作用更加明显,并且随着入射角度θ 的增大,山脊右侧脚点出现地震响应的时间晚于左侧脚点且峰值更大,位移时程曲线变化更复杂。
(3)SV 波入射下层状半空间与均匀半空间圆弧凸起地形的地震响应存在明显差异,层状半空间的放大效应比均匀半空间的放大效应更加显著,在|(x/a)|≤1.0 范围内,层状半空间的地表位移谱放大系数明显大于均匀半空间的谱放大系数;在|(x/a)|>1.0 范围内,有层状半空间的地表位移谱放大系数小于均匀半空间的放大系数的情形出现。 因此,在进行复杂场地对地震波传播影响研究时,需要综合考虑地表地形和地下波速结构的因素。

