Adiabatic evolution of optical beams of arbitrary shapes in nonlocal nonlinear media
Jiarui Che(车佳瑞), Yuxin Zheng(郑喻心), Guo Liang(梁果),†, and Qi Guo(郭旗)
1School of Information and Optoelectronic Science and Engineering,South China Normal University,Guangzhou 510631,China
2School of Electrical and Electronic Engineering,Shangqiu Normal University,Shangqiu 476000,China
Keywords: nonlocal nonlinearity,variational approach,Hermite-Gaussian beam
1.Introduction
The optical Kerr effect is one of the most important effects in the field of nonlinear optics.[1]Due to the optical Kerr effect, light intensity can cause nonlinear change in the refractive index of optical materials,namely nonlinear refractive index (NRI).For the optical material such as nematic liquid crystal,[2]thermal nonlinear liquid,[3]lead glass,[4]and nonlinear ion gas,[5]the NRI at a certain point is not determined solely by the light intensity at that point, but also depends on the light intensity in its vicinity.These optical materials with such nonlocal nonlinearity are called the nonlocal nonlinear media.Nonlocal nonlinearity has received extensive attention in the fields of optical spatial solitons[6]and optical spatial shock waves.[7]The nonlocality plays a key role in both solitons profiles and their interactions.[8]Various solitons, including spiralling elliptic solitons,[9]chaoticons,[10]vortex solitons,[11]multipole solitons,[12]and so on, can be supported in nonlocal nonlinear media.In addition, the nonlocality can overcome the repulsion between in-phase dark[13]or out-of-phase bright solitons,[14]thus making it possible to form bound complex states.Especially, in the nonlocal nonlinear media the structured beams can exhibit novel dynamical behavior.Under the effect of nonlocality, a single Airy soliton can propagate along a parabolic trajectory.[15]With the aid of nonlocality,an Airy Gaussian vortex beam with larger amplitude can be obtained,[16]which always collapses in local nonlinear media.
According to the ratio of the characteristic length of the response function to the beam width, the degree of nonlocality of a nonlocal nonlinear system can be roughly classified into the following four cases: local, weakly nonlocal, generally nonlocal, and strongly nonlocal.[17]In the strongly nonlocal case, the equation governing the nonlinear evolution of optical beams can be linearized to the well-known Snyder-Mitchell model, which owns an exact soliton soluions called the accessible soliton.[18]As for generally nonlocal case, the approximate solution can be obtained by the variational approach to discuss the evolution of optical beams,[19]and the approximate results are in agreement with the numerical simulations.Recently,the relevance between the nonlocality and the focusing and defocusing states in a nonlocally nonlinear system with a sine-oscillation response function is found.[20]The transition between the focusing nonlinearity and the defocusing nonlinearity can happen when the degree of nonlocality of the system changes.Furthermore, it is found that the fundamental Gaussian beam can adiabatically propagate if the characteristic length of the media varies slowly enough.[21]However, we do not know whether this kind of “adiabatic evolution” is universal.Can the adiabatic evolution can still happen for all beams of arbitrary shapes? It is well known that the Hermite-Gaussian functions constitute an orthogonal and complete set,[22]and all beams can be synthesized by Hermite-Gaussian beams of different orders.We find that the adiabatic evolution is valid for the Hermite-Gaussian beams of any order.Therefore, the “adiabatic evolution” is indeed universal in the nonlocally nonlinear system.
2.Theoretical model
The evolutions of 1+1-dimensional optical beams in nonlocal nonlinear media can be described by the nonlocal nonlinear Schr¨odinger equation(NNLSE)[18]
whereφ(x,z)is a paraxial beam,zdenotes the evolution coordinate,xis the transverse coordinate, and Δn(x,z)is the nonlinear refractive index change induced by light fields, which can be expressed as[17]
whereR(x) is the response function of the medium to optical beams.The response functions discussed widely are positive definite and localized, such as the logarithmic response function[23]in the lead glass, the exponential-decay response function in the nematic liquid crystal for the (1+1)-D case[24]and the zeroth-order modified Bessel function for the (1+2)-D cylindrically symmetrical case.[25]Recently, the sine-oscillation function has gradually drawn the attentions of researchers.[20,26-28]In this paper,we take Gaussian response function
and consider that the characteristic lengthwm(z)can vary with the propagation distancez.The characteristic length represents the spatial occupation scale of the response function in nonlocal nonlinear media.In other words, the characteristic length implies the ability to affect the neighboring optical field by a given optical field at the given point.The larger the characteristic length is,the larger region one optical field can influence.For the choice of the response function(3),there are two points to be illustrated.First,although the Gaussian response is phenomenological,the analytical solutions can be obtained in this case.In addition,the physical properties do not depend closely on the specific shapes of the response functions for the nonlocal nonlinear media.[29]Second, it is possible to design az-dependent response in actual nonlinear media along the propagation directions of beams.For example,in the nematic liquid crystals the characteristic length of the response functionwmis found to depend closely on the bias electric field.[25]If the nematic liquid crystal cell has the trapezoidal cross profile(upper and lower surfaces along propagation coordinateszare not parallel), the thickness will be linearly varied.When the bias voltage is applied between upper and lower surfaces of the cell,the linearly varying electric field,then the linearly varyingwm,can be achieved.
3.Variational results and discussions
We can discuss evolutions of optical beams in nonlocal nonlinear media when the characteristic length of the response function varies with propagation distances with the aid of variational approach.It is known that[19]the choice of the trial function for the variational approach is crucial,which should be close to the exact solution of the nonlinear Schr¨odinger equation.In the case of the Gaussian response, it has been demonstrated that the soliton solutions of the NNLSE exhibit the profiles similar to Gaussian ones when the degree of nonlocality goes from the strongly nonlocal limit down to the local limit.[2]Therefore, we take the Gaussian trial solution when the characteristic length of the response function is slowly varying.[21]It is also applicable to choose the Hermite-Gaussian function,the higher-order mode of the Gaussian modes, as the trial function.We take the following Hermite-Gaussian trial beams:
the process is the same as that for any higher-order Hermite-Gaussian modes.[19,30]
The Lagrangian density function of the system described by the NNLSE is[30]
Substituting the trial solution (5) into Eq.(6) and integrating yield the Lagrangian function of the system as
where the primes denote the derivatives with respect toz.Following the standard procedures of the variational approach,[19]we can obtain the variations ofLwithψ,c,c',wandA,respectively.Among them,

from variations toAandwwe can obtain
Substituting Eqs.(8)and(9)into the first derivative of Eq.(8),we then have the differential equation about the beam width as follows:
Under the strongly nonlocal case,i.e.,wm ≫w,
which is the same as the case of trial Gaussian beams discussed in Ref.[21].It means that the evolution of the beam width does not matter with the order of the Hermite-Gaussian beams even if the characteristic length varies with propagation distances.The first and last two terms on the right-hand side of Eq.(10)correspond to linear diffraction effect and nonlinear effect,respectively.When the two terms are equal, linear diffraction effect and nonlinear effect reach an accurate balance.Letting Eq.(10)equal zero,we obtain the critical power
For a fixedwm, Hermite-Gaussian beams will be solitons when the initial input powerPequalsPs.[31]
We first consider the simplest case,that is,
the variation ofwmis linear with respect tozas shown in Fig.1(a).We setP=PsandP=1.5Ps,respectively,to make the beam in soliton state and breather state at the beginning.

Fig.1.(a) Variation of wm on propagation distance z; (b) evolution of beam intensity for P=Ps; (c) evolution of beam intensity for P=1.5Ps; (d) evolution of beam width for P=Ps; (e) evolution of beam width for P=1.5Ps.The plots are for the first-order Hermite-Gaussian soliton and breather,respectively.The optical intensity is I(x,z)=|φ(x,z)|2,which is the same hereafter.
After propagation distancez= 20,wmis gradually increased, the self-focusing effect becomes weaker.Both the minima and the maxima of the beam intensity decrease with the propagation distancez, as shown in Figs.1(b) and 1(c).Aswmdecreases from its maximum atz= 50, the inverse evolution appears.Whenwmrecovers to its initial value, the soliton state or breather state comes back.It illustrates that the first-order Hermite-Gaussian breather can evolve adiabatically.We also checked evolutions of Hermite-Gaussian beams of other orders,and found that the adiabatic evolution all can occur as long as the characteristic length varies slowly with propagation distances.Here the term“adiabatic evolution”is only a borrowed concept,which is related to the adiabatic theorem of Hamiltonian in quantum systems.[32]The quantum adiabatic theorem gives the evolution of the eigenstates when the Hamiltonian changes very slowly.Yet, in this paper we discuss the evolution of optical beams in nonlocal nonlinear media when the characteristic length of the response function changes slowly from one value to another.The two problems are similar although they belong to different fields.
In fact,the adiabatic evolution does not depend on the the concrete variation forms of the characteristic length.In order to show this point, we adopt the sinusoidally varying characteristic length
as shown in Fig.2(a),and numerically simulate the evolutions of Hermite-Gaussian beams of the second,fourth,and seventh orders.The results are summarized in Figs.2(b)-2(e).

Fig.2.(a)Variation of wm;the induced evolution of intensity for the second-(b),fourth-(c),and seventh-order(d)HG breathers when P=1.5Ps;(e)evolution of beam width for the fourth-order HG breather at varied wm given in(a)when P0=1.5Ps.The insets in(e)show the comparison between numerical simulations (red solid curves) and variational results (blue dashed curves).The numerical simulation in this study takes the split-step Fourier method.[22]
Whenwmcomes back to its initial value after one period,the beams all can adiabatically restore to their own original states.The variational results agree well with the numerical simulations.Then we investigate the adiabatic evolution of another structured beam
which cannot be regarded as solitons of the NNLSE (1), and therefore can be regarded as an “arbitrary” beam.Following the same procedures of the variational approach as given above,we can obtain the differential equation about the beam width
From the evolution process shown in Fig.3, it can be found that this special beam indeed can propagate adiabatically.
We also tested the beam ofφ(x,0) =Aexp(-|x|), and simulated its propagation in nonlocal nonlinear media whenwmslowly varies.The simulation results are shown in Fig.4,indicating that the adiabatic evolution can still exist.
In the end, we discuss the evolution of optical beams when the characteristic length changes dramatically, for example,
as shown in Fig.5(a).With the characteristic length increasing from one value to another one in relatively quickly manner,the Hermite-Gaussian solitons of different orders will evolve into breathers of larger widths.When the characteristic length increases,the nonlinearity experienced by optical beams drops,then the beams will expand, which can be confirmed by the increase of beam width shown in Fig.5(b).At the new value of the characteristic length,the original solitons can not maintain their soliton states anymore due to the rapid change of the characteristic length.However,if the characteristic length changes slowly enough, the solitons can smoothly transit to the different ones of different widths, which is just the case discussed in Ref.[33].

Fig.3.(a)Variation of wm on propagation distance z;evolutions of optical intensity(b)and beam width(c)of the beam(13)when P=1.5Ps.
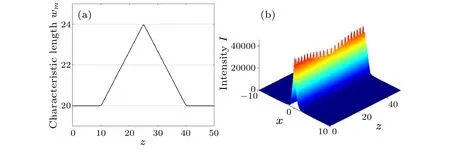
Fig.4.(a)Variation of wm on propagation distance z;(b)evolutions of optical intensity of beam 125exp(-|x|).

Fig.5.(a)Variation of wm on propagation distance z given by Eq.(15);(b)evolutions of beam width for Hermite-Gaussian solitons of different orders.The optical power is set as P=Ps.
4.Conclusion
The evolution of Hermite-Gaussian beams of different orders is discussed in nonlocal nonlinear media when the characteristic length varies on propagation distance.It is found that all the Hermite-Gaussian beams can adiabatically propagate if the characteristic length varies slowly enough by the variational approach.The variational results agree well with the numerical simulations.When the characteristic length gradually comes back to its initial value after one period, all the Hermite-Gaussian beams can adiabatically restore to their own original states.It is proved that optical beams of arbitrary shapes can realize their adiabatical evolution in nonlocal nonlinear media of gradual characteristic length.The results supply a tool to engineer the beam propagation states in actual nonlocal nonlinear media.
Acknowledgments
Project supported by the Key Research Fund of Higher Education of Henan Province,China(Grant No.23A140021),the Open Subject of the Key Laboratory of Weak Light Nonlinear Photonics of Nankai University (Grant No.OS21-3), and the International Scientific and Technological Cooperation Projects of Henan Province, China (Grant No.232102520001).
- Chinese Physics B的其它文章
- Corrigendum to“Reactive oxygen species in plasma against E.coli cells survival rate”
- Dynamic decision and its complex dynamics analysis of low-carbon supply chain considering risk-aversion under carbon tax policy
- Fully relativistic many-body perturbation energies,transition properties,and lifetimes of lithium-like iron Fe XXIV
- Measurement of the relative neutron sensitivity curve of a LaBr3(Ce)scintillator based on the CSNS Back-n white neutron source
- Kinesin-microtubule interaction reveals the mechanism of kinesin-1 for discriminating the binding site on microtubule
- Multilevel optoelectronic hybrid memory based on N-doped Ge2Sb2Te5 film with low resistance drift and ultrafast speed

