State transfer and entanglement between two-and four-level atoms in a cavity

Si-Wu Li(李思吾), Tianfeng Feng(冯田峰), Xiao-Long Hu(胡骁龙), and Xiaoqi Zhou(周晓祺)

School of Physics,Sun Yat-Sen University,Guangzhou 510275,China

Keywords: quantum state transfer,quantum entanglement,cavity quantum eletrodynamics

1.Introduction

At present,most theories and experiments about quantum information are based on two-level systems, so-called qubits.However, in the microscopic world, atoms,[1-3]photons,[4-6]and solid-state systems[7-9]actually possess more than two eigenstates,which allows us to store and handled-dimensional quantum information in a single qubit named qudits.Compared to qubits,such systems have exponentially increased information capacity and show enormous potential in constructing high-dimensional quantum gates to boost the performance of quantum computation.[10-12]Qudits can also locally implement complex Hamiltonian in quantum simulations, such as the discovery of new gauge fields for new physics,[13,14]and quantum chemical dynamics involving molecular or atomic vibrations.[15]Furthermore, one can use qudit systems to realize entanglement in more complex structures[16-18]and stronger Bell non-locality,[19]and to explore the boundaries of entanglement of physical systems.

In order to manipulate qudits, coupling well-studied qubits to qudits is a promising way.Thus, it is necessary to study the connection and state transfer between the particles with different dimensions, such as multiple qubits and qudits, in a hybrid-dimensional system.[20]Recently, various approaches were proposed to implement state transfer in the same-dimensional system by employing the cavity-assisted Raman process[21,22]and resonant cavities,[23,24]which all require cavities with high quality factors.Besides, the direct interaction between qubits can also be used to realize state transfer without the restriction of the cavity’s quality,[25]and it is widely adopted in the solid-state quantum system for fast and scalable quantum information processing.Inspired by these schemes,constructing the interaction between qubits and qudits in quantum electrodynamics (QED),[26-28]which describes photon-atom or atom-atom interaction and has been used to realize quantum logic operations,[29-31]can also achieve the state transfer.Moreover,long-distance quantum teleportations[32-34]are based on quantum entanglement channels,and those entangled states are also prepared in samedimensional quantum objects.Researchers have proposed a number of schemes to prepare entanglements between atoms in QED systems.[35-37]To realize a possible quantum teleportation communication channel,we can also utilize QED to generate a special entanglement in a hybrid-dimensional quantum system.

In this paper,we propose a cavity QED-based scheme to construct photon-induced qubit-ququart interaction that enables us to implement quantum state transfer between two qubits and a single ququart.Using this coherent interaction and photon-number-dependent shift, arbitrary states in two qubits can be encoded into the ququart and vice versa with high-fidelity.Our proposed scheme can also be used to robustly and noise-resistantly generate a maximum entanglement between two-dimensional and four-dimensional systems,i.e., to prepare an asymmetric maximally entangled state(the AMES or(2,2,4)entangled state).[38]Such an entangled state can be potentially used to establish a teleportation interface for atoms possessing different levels.Unlike previous implementations on linear optics, our approach can prepare the (2, 2,4) entangled state efficiently and determinately.We believe our scheme can be extended to the case of multiple qubits and qudits of more dimensions as the structural complexity of the light fields increases.

Our paper is organized as follows.In Section 2, we introduce the system of the proposed scheme and derive an effective Hamiltonian for transferring the information between hybrid-dimensional systems.Then we discuss the statetransfer process in two different cases with or without the ACStark phase shift.Section 3 further studies how to utilize a modified system to prepare AMES in high fidelity.In addition,Section 4 presents some discussions on our schemes, such as the error from system’s imperfection and the influence of decoherence in the system.Finally, we make a conclusion for our state transfer and entanglement preparation scheme,and a vision of the future.

2.Coherent state transfer between two qubits and a ququart

2.1.The model

Our target is to construct a cavity QED system,in which quantum information can be transferred from two qubits to a ququart,i.e.,

where the first and second entries in the kets represent states of qubits A and B, respectively, while the third entry represents the states of the ququart.

We consider a system consisting of two qubits and one ququart coupled with the same cavity via two orthogonal polarized photonic modesaandb, whose exciting frequencies areωca.The atomic qubits have transition dipoles with degenerate excited frequenciesωat, and couple to modesaandb,respectively.The single ququart atom possesses two singleexciton states and one biexciton state, whose transitions also interact with two cavity modes.Figure 1 depicts the level structures of qubits and the ququart.The system’s Hamiltonian can be written as(throughout the paper, ¯h=1)

Here, we consider a Jaynes-Cummings type interaction between multiple atoms and cavity modes with coupling strengthsgAandgB, respectively, which are identical for the same polarization.The collective dipole operators read

whereσn=|g〉n〈e|n, which is the lower operator of the twolevel system.

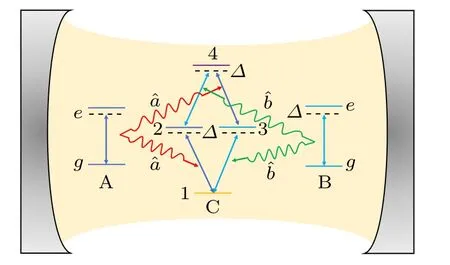
Fig.1.Sketch of the atomic level structure and coupling field mode in our proposed scheme.Two-level atoms A and B interact with polarized field modes a (red arrow) and b (green arrow) respectively.The fourlevel atom contains orthogonal transition dipoles interacting with polarized field modes.

When the energy of the cavity fields does not match the exciting energy of the atomic system, the effective interaction would be weakened, and there is no energy exchange between them.Cavity modes can be virtually excited, and the second-order interaction dominates the system’s dynamics, where qubits and the ququart exchange their excitations.In this case, we can use this cavity QED model to implement the quantum state transfer, while the decoherence of the cavity is suppressed.We perform the Schrieffer-Wolf transformation[39]

onHto adiabatically eliminate cavity modes in the system’s evolution,where the detuning satisfiesΔ=|ωca-ωat|≫gA,gB.After the transformation,the effective Hamiltonian of the system becomes

where

The second and fourth terms in Eq.(5) describe the qubitququart interaction,while the third and fifth terms denote the photon-number-dependent shift.

With the effective coupling strength,λ ≡-g2A/Δ=-g2B/Δand the photon-number-dependent phase shift inHeff,this cavity QED system can achieve the state transfer.First,we assume thataandbmodes initially are both in vacuum states so that the effective Hamiltonian in Eq.(5) can be projected into the photon-vacuum subspace,i.e.,

Because Eq.(1) contains states in different subspaces with the particle-exchange interaction,the state evolution could be written as

whereαµνandβµνrepresent normalized amplitudes for their corresponding subspaces.Note that we have omitted the cavity’s degree of freedom.WithHeff,vac,the two-qubit state will be transferred to the ququart att=π/(2λ),

It indicates additional minus signs in the final state,which will noticeably decrease the transfer fidelity.For correcting these minus signs,single-qubit phase operations on qubits A and B should be performed, respectively, before the cavity-induced interaction.Then the cavity QED model without the photonic excitation implements the local state-transfer operation with high fidelity.

Furthermore, using the photon-number-dependent phase shift, the system can also achieve a high-fidelity state transfer without single-qubit operations.Initially,the double-mode single-photon state is prepared in the cavity, andHeffin the single-photon subspace is given by

The final state of the evolution is

Finally, a state transfer is realized without performing local qubit operations before the atomic interaction.It is worth mentioning that the effective Hamiltonian requires double-mode single-photon state preparation in the cavity.It is possible to experimentally prepare this single-photon state by exploiting resonant emitters coupling to the cavity.[40,41]Using optical exciting by classical fields on the emitters,the cavity will absorb the excitation of resonant emitters and be in the doublemode one-photon state after the relaxation.However, it introduces additional complexities and makes the state transfer more challenging.In comparison, the vacuum cavity can achieve the state transfer without the need for pre-state preparation, albeit it requires convenient single-qubit operations.Moreover, an ultrahigh-Qcavity is demanded in the doublemode single-photon case to handle photonic loss, while the virtual excitation in the vacuum-cavity case enhances the coherent time of the cavity.

Figure 2 reveals the states’ evolution with the HamiltonianHeff,ph, which contains the single-photon phase shift.At the initial time,αge=αeg=αee=1,and the two-qubit system is separated from the ququart.After a period of time,two systems are entangled and then are separated again att=π/(2λ),while the amplitude information,initially encoded in the twoqubit system, has been transferred to the single-ququart system.The time-dependent fidelity of the state transfer process defined as|〈ψ(t)||ψ(T)〉|2is also shown in Fig.2.The fidelity reaches the maximal value whent=π/(2λ)along the system’s evolution.The amplitude information is transferred back to the qubits aftert=π/(2λ), and it means that the inverse state transfer process can also be achieved with this approach.Note that four terms in Fig.2 sufficiently represent the process of state transfer in Eq.(8) owing to the symmetry of the system’s Hamiltonian(gA=gB).

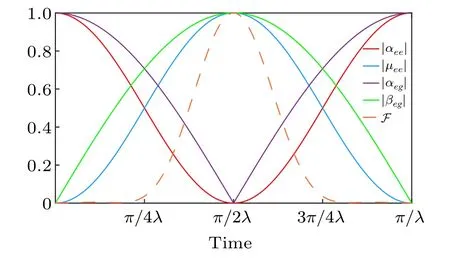
Fig.2.Time-dependent Rabi-type oscillation of the state transfer between 2 qubits and a ququart,with the system’s Hamiltonian Heff,ph.The transfer time is identical to single-and double-excitation subspaces, and amplitudes(solid lines)are transferred synchronously.The fidelity(orange dashed line), F, indicates the phase difference between the transferred state and the ideal state.

In a 2 to 1 state transfer process, one can implement the information interface for a hybrid-dimensional system to transfer two-body information on a single particle.In a reverse process, one can prepare arbitrary whatever entanglement or not two-body quantum state after preparing a single particle state without direct interaction between low-dimensional particles.[20]

In contrast to previous schemes[20,38]that employed probabilistic gates in linear optics, our proposed scheme accomplishes state transfer using an effective qubit-ququart interaction, leading to the evolution described by Eq.(8).In other words, our proposal eliminates the need for state projection measurements, making it an efficient and deterministic approach.

In experiments,the cavity with two orthogonal polarized modes can be realized by a circular resonator[42-44]and the cavity photons possess orthogonal polarization.The diamondtype ququart has been studied and observed in Rb atoms,[45-47]and manufactured by artificial atoms such as quantum dots(QDs)[48,49]and superconducting circuits.[50,51]In the atomic case, the two atomic qubits and the atomic ququart are sent into the cavity, remaining inside the cavity for a duration oft=π/(2λ),[52-55]and then the cavity-induced interaction enables the state transfer to be accomplished.In the solid-state artificial atom case,two-qubit systems and the ququart system are embedded into a cavity, and driving fields interact with them to control the interaction between artificial atoms,[56]with the duration satisfyingt=π/(2λ).

2.2.The validity of the model in the far-detuning regime

With the full Hamiltonian Eq.(2),the time-dependent fidelity is defined as

where

The cavity’s degrees of freedom are not eliminated in the full Hamiltonian,and the photonic Fock states are included in the time evolution.The target photonic state is vacuum,while the energy and information remain stored in the atomic system.

Figure 3(a) displays the time-dependent fidelity for the state transfer under different detuningsΔ, i.e.,Δ/g=5, 10,20,50,respectively.When the detuning presents,photons will be radiated and be quickly absorbed, resulting in a low probability of cavity excitation,P∝(g/Δ)2.WhenΔ/g=5, the fidelity exhibits obvious oscillations,and it does not reach the maximum value atλt=π/2 due to the excitation of the cavity modes.The approximation in Eq.(5)is unreliable because the detuning is not large enough.The oscillation is weakened as the detuning increases because of the more rapid and weaker evolution of photons.WhenΔ/g=10, the system achieves a fidelity ofF(π/(2λ))＞0.99, as shown by the dark blue line in Fig.3(a), indicating that the adiabatic elimination of cavity modes takes effect.AsΔ/g=20 andΔ/g=50,the oscillation is inconspicuous,and the maximal values almost approach 100%.The maximal fidelity is mainly affected by the photon excitation,and the error is given by 1-F∝(g/Δ)2.

Fig.3.(a)Time evolution of the fidelity for state transfer, using the full Hamiltonian,with different values of Δ/g,namely,5,10,20,and 50,respectively.(b) The error is a function of the deviation from interaction time,and the operational time is defined as top ≡π/2.

These results demonstrate that the state transfer using the full Hamiltonian can be effectively described by the Hamiltonian given by Eq.(5)in the far-detuning regime.Specifically,for detunings satisfyingΔ=10g,the system achieves a fidelity greater than 0.99.For a more stable fidelity,the detunings satisfyingΔ=20gcould be better.

A high-fidelity state transfer requires accurate control of the interaction time due to the oscillation.The deviation from the intended interaction time can significantly affect the fidelity, as shown in Fig.4(b).However, the fidelity becomes more stable with higher detuning.For instance,in the case ofΔ=50gorΔ=100g,the fidelity is still above 0.99 as long asΔt/top＜0.05.

Our state-transfer scheme is accomplished by a local interaction system within a cavity, and we will expand our scheme to generate a special entanglement state, which will be discussed in Section 3.

3.The asymmetric maximal entanglement preparation

In this section, we discuss how to generate the maximal entanglement between two qubits and a ququart by exploiting the original and the modified system Hamiltonian.

To increase the scale of entangled states for more complex applications, one can increase both the number and dimensions of particles,such types of entangled states have been demonstrated.[57,58]Recently, an asymmetric maximal entangled state (AMES or (2, 2, 4) entangled state), consisting of two two-level systems and a single four-level system,i.e.,

has been probabilistically prepared in the photonic system.[38]Because such an entangled state contains particles with different dimensions,it can be used as an interface for the information flow between quantum systems with different dimensions via the quantum state teleportation protocol.

Using our far-detuning cavity QED Hamiltonian in Eq.(7), we can prepare the atomic AMES like Eq.(14) after an evolution time,t=π/(4λ),and atomic entangled state is approximately pure because the cavity is virtually excited.However,the numerical result shown in Fig.4(a)implies that the state evolution is not stable facing the error of the temporal control when the atomic system is in the AMES.

Based on the system in Eq.(2),we introduce a frequency mismatchδbetween qubits and the ququart’s exciton states,and the system Hamiltonian reads

whereωA=ωat-δ/2,ωB=ωat+δ/2, andδ ≪Δ.Again,we apply the Schrieffer-Wolf transformation eSmis toHmisand obtain an effective interaction between atoms,where

Then the final effective Hamiltonian changes to

where we have assumed that field modes are vacuum at the initial time.In the absence of frequency mismatch, the (2,2, 4) state is always able to be generated at a certain time,no matter how the coupling strength is.When the frequency mismatch is introduced,the maximal entanglement can be prepared only as the atomic coupling is strong enough.In order to achieve the maximal entanglement, the effective coupling strength,λ＇≡g2A/(Δ-δ/2)=g2B/(Δ+δ/2),should satisfy

If the equal sign holds,the initial state|gg4〉will evolve to the AMES,saying

where the time intervalPerforming a single-qubit phase operation on qubit A,the minus signs of the first and third terms in Eq.(19)will be corrected.On the contrary, the entangled state prepared by the resonant interaction needs single-qubit operations twice to correct the additional phase,which may introduce more noise than the near-resonant case.

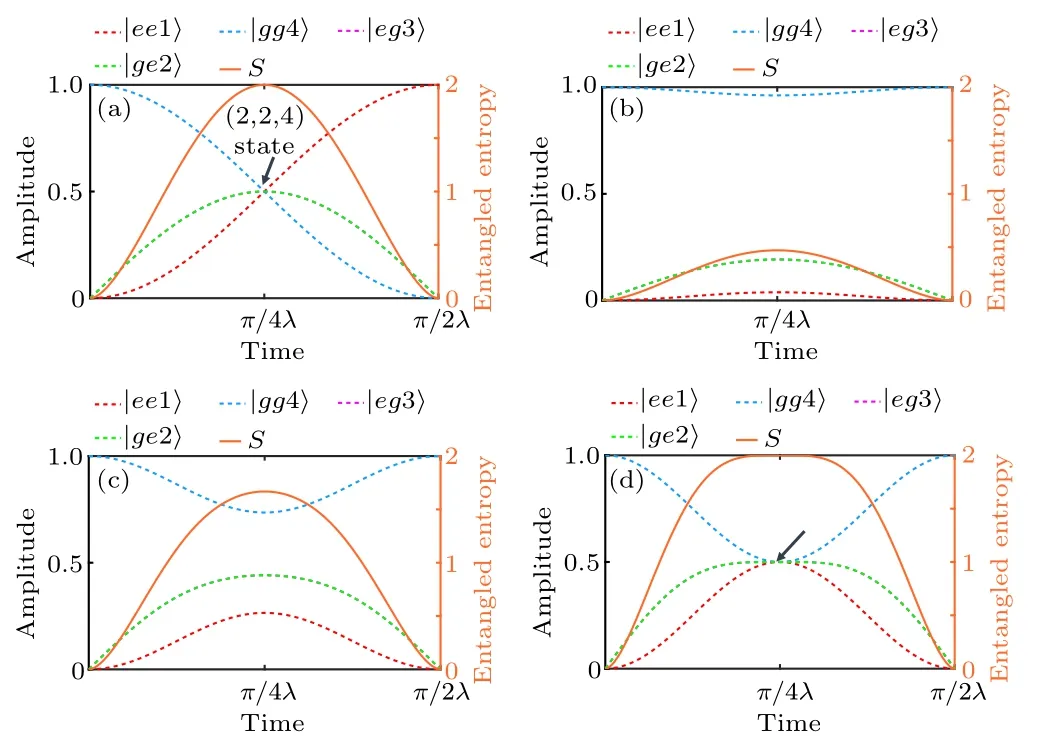
Fig.4.Time-dependent evolution of the(2,2,4)entangled-state preparation (color dotted lines) and the entangled entropy S of the atomic system(orange solid lines)in the cavity QED model.Panel(a)shows the interaction process without the frequency mismatch.Panels (b)-(d) display atomic interaction processes with the frequency mismatch as the coupling strength grows,i.e.,|λ＇/δ|=0.1,0.3,0.5,respectively,and Ω =δ2+4λ＇2.The (2, 2, 4) state obtains as the amplitudes reach their extreme points, where the evolution is smooth and robust to the temporal error.Here, the amplitude of |eg3〉 (pink dotted lines)overlaps with|ge2〉(green dotted lines).

In the resonant case(δ=0),the performance of information exchange between qubits and the ququart is unweakened,therefore the state transfer can be obtained att=π/(2λ).This timing corresponds to the inflection point in the evolution,ensuring a steady process.The AMES is an intermediate state and is generated att=π/(4λ),which is a fast-changing timing.Whenδ/=0, it weakens the effective coupling and the information-exchange capability between qubits and the ququart.Consequently, the state transfer cannot be accomplished, and the maximal entangled entropy that the system can achieve may change withδ.Forδ ≤2λ, the effective coupling is sufficiently strong to generate maximal entanglement(S=2),even though the quantum information cannot be completely exchanged.Notably,δ=2λserves as the boundary for generating AMES att=π/Ω, corresponding to the inflection point of the evolution.In the case ofδ ＞2λ,maximal entangled entropy of the atomic system becomes lower asδincreases due to the weaker effective coupling.Overall, a mismatchδmodulates the information-exchange capability of the atomic system and the state in the inflection point providing tardy evolution.

4.Discussion

In the previous sections,we present some analyzed results regarding the state transfer and entanglement between twoand four-level atoms using an effective Hamiltonian.However, in experimental implementations, the imperfect control of parameters and the presence of decoherence in the system can affect the three-atom operations.In this section, we will discuss these sources of errors in detail.Additionally,a generalization to the higher-dimensional case will be provided using a specific Hamiltonian.

4.1.The deviation of the temporal control

The duration of the atom-cavity interaction can be controlled by the time of atoms staying in the cavity or the driving fields.However,if the control is not precise enough,the deviation in time can decrease the fidelity of the three-atom operations.In the far-detuning regime,the error of the fidelity for the state transfer can be evaluated using the effective Hamiltonian in Eq.(5),and take the form of

whereδtis a small deviation of the interaction time.Moreover,the error in generating the AMES can be expressed as

4.2.The asymmetric coupling

If the electric field strength of the cavity modes are not identical, another important source of error is the asymmetric coupling due to the difference ofgAandgB, leading toλA/=λB.Assuming thatλA=λ0+δλ/2 andλB=λ0-δλ/2,whereδλis a small value, the error for transferring an arbitrary quantum state encoded on the two qubits takes the form of

Surprisingly, to generate the AMES with asymmetric coupling,the fidelity att=π/(4λ0)reads

which means the generation of the AMES is robust to the asymmetric coupling.In the double-excitation subspace,eigenenergies of the effective Hamiltonian areλA+λBand 2(λA+λB).Adopting definitionsλA=λ0+δλ/2 andλB=λ0-δλ/2,the eigenenergies remain 2λ0and 4λ0,which ensures the robustness of the system.

4.3.The decoherence of the system

In the far-detuning regime,the requirement on the quality factor is relaxed,because the qubit-ququart interaction is realized by the virtual-photon exchange.The cavity is excited in low probabilityP∝(g/Δ)2, and the effective lifetime of the photons is prolonged.For the state transfer, the fidelity will be affected by the photonic lifetime 1/κ, the atomic excited lifetime 1/γ, the total excitationNand the detuningΔ.As the detuning increases,the interaction time could be comparable with the excited lifetime of atoms.Dynamics of the entire system with decoherence can be described by the dissipative quantum master equation,which can be expressed as follows:

whereD(O)ρ=OρO†-(O†Oρ-ρO†O)/2 represents the dissipative superoperator.

For example, a cavity QED system consisting of three atoms within a high-Qmicrowave cavity can obtain singleatom coupling constantg=2π×24 kHz,[59-61]and the resonance frequency of the cavity is about 50 GHz.With the choice ofΔ=10g, the interaction time for the state transfer isπ/(2g2/Δ) = 1×10-4s, which is much faster than the excited lifetime 1/γ= 3×10-2s[59-61].For a cavity with quality factorQ=107and decay rateκ=0.2gresulting in a cooperativityC=g2/(2κγ)=104, the effective lifetime is 3×10-3s much larger than the interaction time.The fidelity for state transfer ofis approximately 0.97.Using a cavity withQ=108, the fidelity can exceed 0.98.

Furthermore, the choice of the far-detuning condition can efficiently generate the maximal entanglement among the three atoms, while in the resonant case, the atoms become highly entangled with the cavity fields during the evolution.

The result of the master equation is depicted in Fig.6.As the detuning is not so large, the decoherence of the cavity significantly affects the fidelity of the state preparation.With a set of parameters discussed above, i.e.,κ=0.2gandγ=2.2×10-4g(Q=107andC=104), the maximal entangled state is generated att=π/(4λ)with fidelity ofF=0.969 and 0.975 as the detuningΔ=20gand 50g, respectively, as shown in Fig.6(a).As the detuning increases, the influence of photonic decay will weaken.A cavity with a higher quality factor can improve the fidelity, as depicted in Fig.6(b)withκ= 0.02g(Q= 108andC= 105).The fidelityFis larger than 0.985 with detuningΔ=10g, and it still exceeds 0.975 with detuningΔ=20g.However, the interaction time is larger, and the decoherence of atoms affects the preparation, as shown by the case ofΔ/g=50.Furthermore, another consideration is that three atoms are placed into an optical cavity whose resonance wavelength is in the region of 630 nm-850 nm.[62-64]The system with predicted parameters(g,κ,γ)/2π=(700, 3.5, 2.62)MHz(Q ≈108)can achieve state transfer and generation of the AMES with fidelity more than 0.939 asΔ=10g,while fidelity decreases to 0.89 in the case ofΔ=20g.In the experiment, to achieve high fidelity state transfer and entanglement generation,a suitable detuning should be determined by considering both the cavity’s quality factor and the coherence time of atoms.

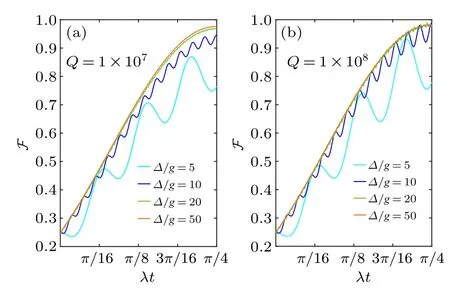
Fig.5.The time evolution of the fidelity for preparing the (2, 2, 4) entangled state,with(a)the quality factor Q=107 and the atom decay rate γ =2.2×10-4g,and(b)the quality factor Q=108.

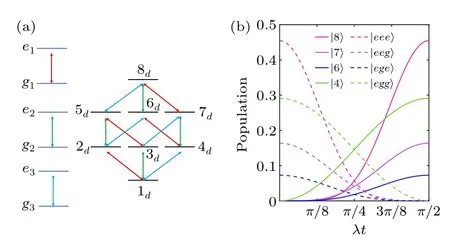
Fig.6.(a)The level structure and transitions of three qubits and a qudit with eight eigenstates.(b) The transferring process of the population of qubit’s state(dashed lines)and qudit’s state(solid lines).

4.4.The generalization to the higher-dimensional case

This scheme can be expanded to higher-dimensional systems.Assume that there areNqubits constructing a 2Ndimensional Hilbert space, and another single qudit hosts 2Neigenstates.All of theseNqubits and the qudit interact with theN-modes electromagnetic fields which are described by bosonic operators,ananda†n.There areM ≡2N-1special transitions{Jn,j}in the qudit interacting with theanfield,and the collective transitions reads

The interaction between qubits,the qudit,and fields takes the form of

This interaction Hamiltonian can implement the state transfer in the far-detuning regime, and the effective interaction with vacuum field modes can be written as

We can consider the specific case of three qubits and one qudit withd=8.The level structure and the transitions of these particles are displayed in Fig.7(a).The collective transition operators are given by

and they interact with field modea†1,a†2,anda†3,respectively.As shown in Fig.7(b), the population of the three atoms can be transferred to the 8-level qudit att=π/(2λ),starting from the initial three-qubit state

We should note that while the interaction time remainst=π/(2λ),the number of parameters in the Hamiltonian increases rapidly, making it more challenging to control them.An analysis on the decomposition of a qudit operator into multiple qubits[65]may be helpful for the generalization of qubitqudit operations to the higher dimensional system.

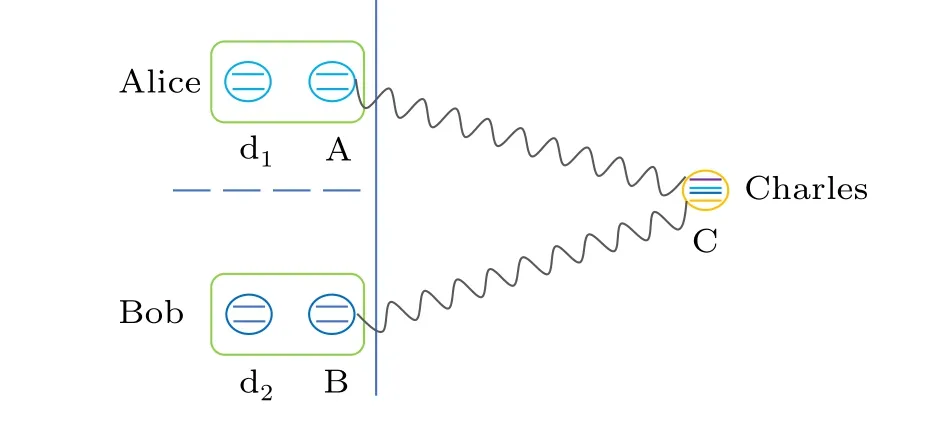
Fig.7.Sketch of the quantum state teleportation from two uncorrelated qubits to a single ququart, and the asymmetric maximal entangled state serves as a communication channel.

4.5.Quantum teleportation between two qubits and a ququart

With the previous efficient preparation of the AMES, it is possible to make use of this entanglement channel to implement quantum state teleportation for atomic qubits and an atomic ququart.Here,we introduce a potential quantum teleportation protocol based on the AMES[38]to teleport quantum information initially encoded on the two-qubit system to a ququart.First, two qubits, A and B, and a ququart C are coupled through a waveguide resonator.[66-68]After an appropriate time, they are prepared in the (2, 2, 4) entangled state,and then they are decoupled.Assume that Alice, Bob, and Charles hold qubit A, qubit B, and ququart C, respectively.Alice and Bob also hold qubits d1and d2of other qubits pair,whose unknown quantum state can be written as

Before measurements and operations,the combined state of all above five particles is

We can also expand this scenario to teleport a single ququart information to a pair of qubits via the(2,2,4)entangled state by employing 4-dimensional Bell measurement[70]on the source ququart and the entangled ququart.The measurement result determines the 2-dimensional unitary operation on qubits of the(2,2,4)entangled state.

In recent years,significant researches have been devoted to exploring high-dimensional teleportation,[71-73]which all focus on information transfer between particles in the samedimensions.The protocol we introduced above utilizes a type of entangled states with asymmetric particle numbers,and allows state teleportation between multiple objects and a single object.It fundamentally differs from those schemes of highdimensional quantum teleportation,as the latter implement the information transfer between individual particles.

5.Conclusion

We discuss the state transfer and the entanglement generation between 2- and 4-level atoms within a cavity to implement an information interface for quantum particles in different dimensions.We derive an effective qubit-ququart interaction with the far-detuning condition,which allows suppressed decoherence of the cavity.Our cavity QED scheme can obtain a high-fidelity transfer process for arbitrary two-qubit quantum states and its inverse efficiently, without measurements and post selections.Moreover, the proposed scheme can be made use of determinately preparing the atomic asymmetric maximally entangled state, and we find there is a bound of atomic coupling strength for generating the AMES in high fidelity.This high-fidelity preparation could be possibly applied in the quantum state teleportation between qubits and a ququart.The cavity QED would be a promising method to establish an interface for information communication between particles with different dimensions.

As a prospect,a quantum storage protocol is expected to be implemented, where the information from multiple qubits can be stored in a multi-level atom.Specifically,through Raman transitions, i.e., a combination of classical driving fields and multi-mode photonic channels,[21,74]multiple qubits’state will be transferred to multi-level atom’s ground states, which allows a long lifetime of the storage.Multiple such highdimensional atomic registers could be a promising platform for distributing quantum information in quantum networks.Furthermore,a non-local entanglement between qubits and qudits can be achieved in waveguide QED,where unidirectional coupling between quantum systems can prepare steady entangled states.[75,76]This cascaded architecture has potential for realizing quantum state teleportation in hybrid-dimensional systems.

Acknowledgments

Project supported by the National Natural Science Foundation of China (Grant No.61974168), the National Key Research and Development Program of China (Grant No.2017YFA0305200),and the Special Project for Research and Development in Key Areas of Guangdong Province of China(Grant No.2018B030325001).

We thank Ze-Liang Xiang for very stimulating discussions.Part of the simulations are coded in MATLAB.