Eigenstates and temporal dynamics in cavity optomagnonics

Yun-Jing Ding(丁云静) and Yang Xiao(肖杨)

1School of Physics,Nanjing University,Nanjing 210093,China

2Department of Physics,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China

Keywords: magnon,spin wave,cavity

1.Introduction

Due to the strong coupling between magnon and microwave cavity photon, a hybridized quasiparticle emerges which was dubbed cavity magnon polariton.[1-3]It can be both magnon-like and photon-like and thus can be manipulated by magnetic and optical means.Currently, several characteristic features have been revealed based on frequency domain measurement,e.g.,microwave transmission spectrum.[4-16]Compared to the studies in the frequency domain,the temporal dynamics in the time domain attracts less attention.

According to the interaction mechanism,the coupling between magnon and photon can be of the type of either coherent or dissipative coupling.The former is mediated by the dipolar interaction between magnetization and microwave magnetic field.[4-15,17,18]In the frequency domain,it presents the well-known level repulsion (avoided crossing).In the time domain,the temporal dynamics of level repulsion shows a beat-like oscillation.[7,19-21]As for the level attraction, an important feature in the steady state spectrum is the eigenstates with degenerate eigenenergy, which is usually called level attraction.[22-30]Recently, Grigoryanet al.showed that level attraction of linearly-coupled magnon and photon modes can lead to synchronization.[29]As is known,synchronization is driven by nonlinear interaction between harmonic oscillators.For instance, the synchronization in optomechanic system has been predicted theoretically and observed experimentally in which high-power input laser induces limit-cycle oscillation and synchronization.[31]Therefore,it is important to study temporal dynamics, especially the synchronization, in the time domain for the magnon-photon level attraction.

In many studies of magnon-photon coupling,[1]both modes are in the microwave frequency range for both level repulsion and level attraction.However,the magnon can be coupled to the visible photons as well which has been observed in recent cavity optomagnonic experiments.[32-36]Compared to the microwave photons,visible photons provide more tunability.First, the system can stay in both red-detuned and bluedetuned regimes which reproduces level repulsion and attraction depending on the laser driving frequency.This facilitates the manipulation of the coupling mechanism by the driving light.On the other hand,the interaction between magnon and optical photon is of the coherent nature which is different from the dissipative coupling in cavity magnon polariton.[25,27]By studying the temporal dynamics of cavity optomagnonics, it will provide a full understanding of temporal dynamics and synchronization in the magnon-photon system.

The remainder of this paper is organized as follows.In Section 2, we provide the Hamiltonian for the coupling between magnon and visible photons.The results of eigenfrequencies,eigenstates,and temporal dynamics are given in Sections 3 and 4 for level repulsion and level attraction of coherent coupling.Section 4 is devoted to the comparison of the level attraction of dissipative coupling.Finally, the findings are concluded in Section 5.

2.Hamiltonian

The interaction between magnon and optical photon is described by the energy densityεmp= (1/2)εE2with dielectric constantεand electric fieldE.[37]In optomagnonics, the dielectric constant of the ferromagnetic medium is dependent on the magnetizationM, i.e.,ε(M) =εr+f·M+···, whereεris the magnetization-independent dielectric constant andfis a coefficient.Based on the Holstein-Primakoff transformation,[38]the magnetization can be represented by the magnon operator, e.g.,Mx∝(m+m†).Moreover, the quantization of electromagnetic field gives rise to the photon representation of electric field,e.g.,Ex∝(ˆc+ˆc†).Here, ˆm(ˆm†) and ˆc(ˆc†) are annihilation (creation) operators of magnon and photon modes.By inserting the operators of magnon and photon modes intoεmp,we can obtain the photon-magnon coupling Hamiltonian and further write it in the framework rotating at the laser driving frequencyωLas

whereωmandωcare the frequencies of magnon and cavity photons.g0is the coupling strength between magnon and single photons.In this work,we consider that the magnon mode is the uniform precession mode and the cavity resonance mode is the whispering gallery mode.The coupling between these two modes has been studied in recent experiment.[35]

To proceed, we consider the low-power driving and thus linearize Eq.(1) by splitting the cavity field into an average field and a fluctuating term,i.e., ˆc= ¯c+δˆc.Keeping the first order term ofδˆcorδˆc†only,we obtain

where the first and second terms in right hand side represent the beam-splitter interaction and parametric down-conversion interaction, respectively.Depending on the detuning (ωcωL),two regimes can be distinguished.Asωc-ωL≈ωm,the magnon mode ˆmand the oscillatorδˆchave equal frequency.Based on the rotating wave approximation (RWA), the second term ofHintplays a negligible role and the first term ofHintdominates.On the contrary, the RWA dictates that, asωc-ωL≈-ωm,the second term becomes dominant and the first term can be omitted.Such a treatment has been employed in cavity optomechanics[31]and cavity optomagnonics.[35]We next consider these two cases respectively.

3.Level repulsion of coherent coupling

AsωL＜ωc,the magnon absorption events dominate and only the terms of(δˆc†ˆm+ ˆm†δˆc)in Eq.(3)play roles.Hence,the coupled Hamiltonian becomes

where we defineΔc=ωc-ωL.

In order to obtain eigenvalues of Eq.(4), we write the equation of motion

where we usemandcto represent the expectation values of magnon and photon operators, i.e.,m=〈ˆm〉 andc=〈δˆc〉.When the intrinsic dampings are included, the resonance frequencies in Eq.(5)are replaced by complex frequencies,e.g.,˜ωm=ωm-iκmand ˜Δc=Δc-iκcwithκm,cbeing the damping rate of magnon and photon modes.Hereafter,the intrinsic damping is all absorbed in the mode frequencies.For the sake of simplicity,we consider that both modes have equal damping rates,i.e.,κm=κc.

The eigenfrequencies and eigenstates can be obtained by diagonalizing the matrix in Eq.(5),i.e.,

whereΔmc= ˜Δc- ˜ωm.Figure 1(a) shows the real part of eigenfrequency and polarization of eigenstates.The polarization of eigenstate is directly determined from the eigenvector in Eq.(7).The classification of polarization of eigenstate is analogous to that of electromagnetic wave.Through normalization of the eigenvector in Eq.(7), the eigenstates belong to linear polarization as two elements are both real.When one of two elements becomes complex, the eigenstate is elliptically polarized.Especially, as two elements have equal amplitudes and one is real while another is pure imaginary,the polarization of eigenstate becomes circular.The polarizations of eigenstates reflect the relative phase of magnon and photon modes in the hybridized magnon-photon state.For instance,the relative phase is 0 orπfor linear polarization while is±π/2 for circular polarization.

The spectrum in Fig.1(a) shows a clear level repulsion,which is a well-known feature of the coherent beam-splitter interaction.[1,31]Two eigenvectors of level repulsion are orthogonal, which holds for any frequency detuning.At resonance,i.e.,Δmc=0,two eigenvectors are(1,±1)T,indicating the largest degree of magnon-photon hybridization.As the detuning increases,the hybridized states gradually evolve into the bare magnon and photon states.With eigenfrequencies and eigenvectors,the temporal evolution of Eq.(5)can be analytically written as a linear combination of two eigenvectors

wherea1anda2are two constants which are determined by the initial condition.The method given in the formula Eq.(8)is intrinsically equivalent to the coordinate transformation method[20]used recently to study the transient response of level repulsion.Due to the absence of an external driving source, Eq.(8) describes the transient response, e.g., a pulsed microwave experiment.[7,20,21]Different from conventional continuous-wave driving, a pulsed microwave driving is realized by injecting a pulse, switching it off after a short time and then monitoring the free decay process.Such pulsed measurements have been conducted in recent experiments of cavity magnon polariton.[7,20,21]

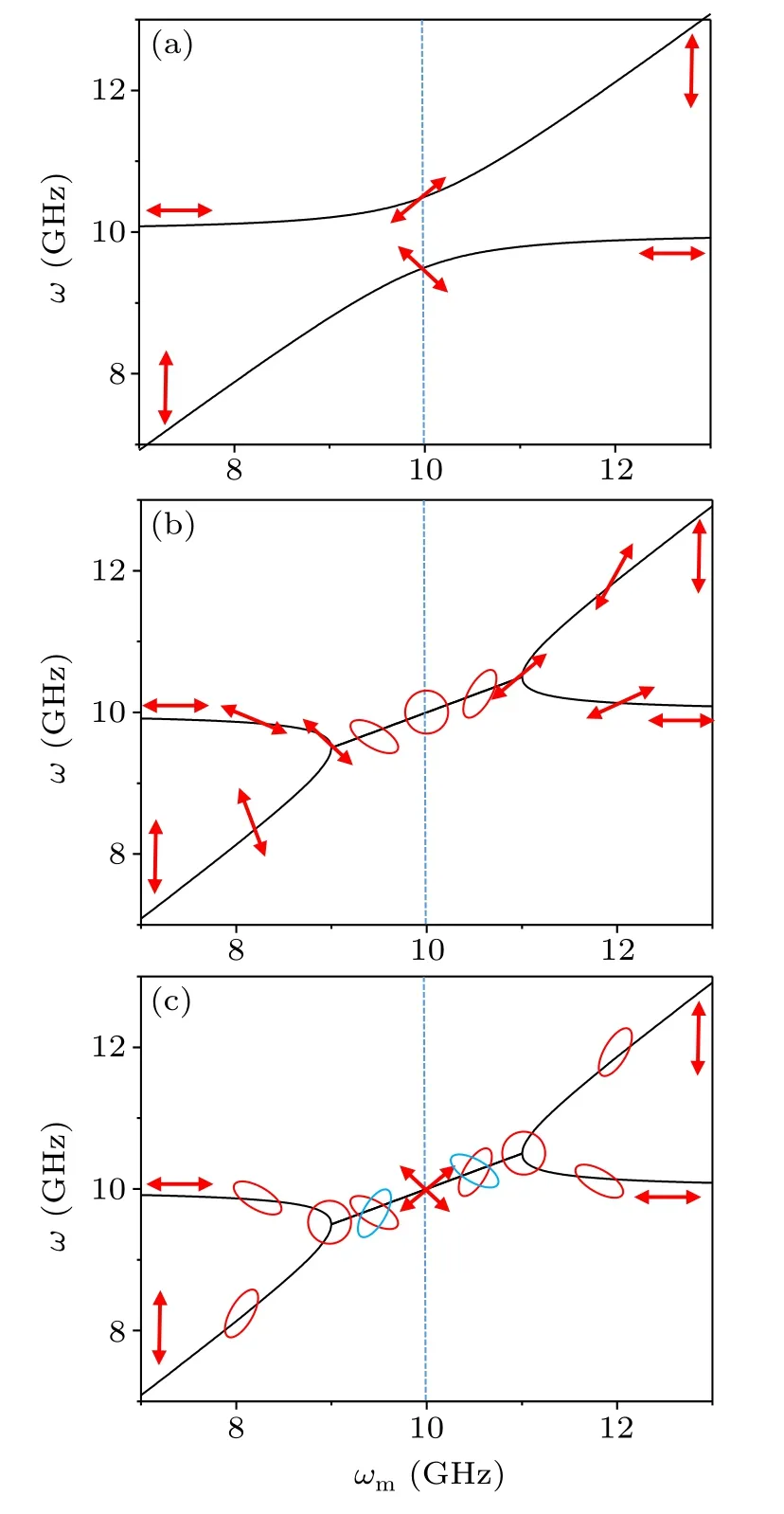
Fig.1.Spectrum and polarization of eigenstates of (a) level repulsion and (b) level attraction of coherent coupling between magnon and visible photons.In panel (c), we show the results of the level attraction of dissipative coupling between magnon and microwave photons.The polarization of eigenstates is described by arrows, circles, and ellipses. ω represents the real parts of eigenfrequencies. ωm is the ferromagnetic resonance frequency.The dashed line marks the resonance with Δcm =0.In each figure, we do not consider the intrinsic damping so that we can obtain pure linear and circular polarizations.

At resonance, the time-dependence of photon and magnon amplitudes are written as

Figure 2(a) shows the numerical results of Eqs.(9) and(10).The amplitudes of two modes oscillate with the time periodically.The period of magnon and photon oscillation isπ/g.The oscillations present a beat-like behavior, i.e., the photon amplitude is maximum(minimum)as the magnon amplitude is minimum(maximum).This implies that the energy is coherently exchanged between magnon and photon modes.These results are in agreement with recent experimental measurements and theoretical predictions.[7,20,21]Due to the presence of damping, the magnon and photon amplitudes decay with the rate of 2κc, which is similar to a damped harmonic oscillator.Based on Eqs.(9) and (10), one can see that the magnon-photon synchronization does not occur in the coherent magnon-photon coupling.

4.Level attraction of coherent coupling

AsωL＞ωc, the magnon emission events dominate and the dominant terms in Eq.(3)are written as

where we defineΔc=ωL-ωc.

The dynamical equation reads

The eigenfrequencies and eigenstates are expressed by

The spectrum and polarization of eigenstates are shown in Fig.1(b).One can see that two modes coalesce to form a lock region near the resonance.The frequency is complex inside the lock region while real outside the lock region.The transition between these two regions is marked by the bifurcation,i.e.,the exceptional points(EPs).An important difference between level attraction and level repulsion is the nonorthogonality of eigenvectors for level attraction.At resonance, the eigenvectors are (1,±i)T.Therefore, the magnon and photon modes are hybridized with a relative phase of±π/2 and both states are circularly polarized.As the detuning increases,the states become elliptically polarized.At the EPs and outside the lock region,they are linearly polarized.

The temporal dynamics of level attraction presents distinct behavior from level repulsion.At resonance,the dynamics is given by

In the weak coupling regime,i.e.,g ＜κcorg ＜κm,both exponential terms on the right hand of Eqs.(15)and(16)decay with time in the long-time dynamics as shown in Fig.2(b).But the first term e-(κc-g)tdecays slower than the second one and thus dominates.In the strong coupling regime,i.e.,g ＞κc,the first term grows exponentially without limit,i.e.,the instability happens.In this work, such an instability arises from the magnon amplification.AsωL＞ωc, the incident driving photon excites magnons in order to enter the cavity and therefore the magnon number or magnon amplitude increases.In weak coupling regime, the magnon growth is suppressed by the intrinsic damping of magnon.As the growth rate equals and exceeds the decay rate,i.e.,in the strong coupling regime,the instability occurs.In such case,the magnon amplitude will be finally saturated by the nonlinear magnon-magnon interaction, which is beyond the scope of this work.Similar instability has been observed in blue-detuned optomechanical system by engineering the dissipation of optical and mechanical modes.[39]

In previous studies, Glauber proposed that an oscillator with negative energy can be used to simulate a quantum amplifier.[40]Experimentally,Kohleret al.implemented such a harmonic oscillator with negative energy to realize instability in the optomechanical system that is made of Rb atoms inside an optical cavity.[41]In this work, the model is of the same Hamiltonian and interaction type with an oscillator of positive energy and another oscillator of negative energy.

Outside the lock region, i.e.,Δ2mc-4g2＞0 and equal damping,the amplitudes are written as

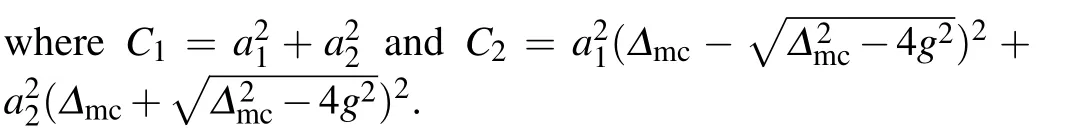
One can see that the magnon and photon amplitudes present oscillation with the period of.In the limit of large detuning, i.e.,g ≈0 andΔmc≈ωc,ωm, the period becomes 2π/ωcor 2π/ωm.Moreover,the magnon and photon amplitudes evolve with time in a synchronizing way shown in Fig.2(c).This is different from level repulsion in which the magnon and photon amplitudes vary alternatively.Such differences can be explained by the coupled Hamiltonian.As for level repulsion in Section 3,the magnon absorption results in the increase of photon energy.The energy is exchanged between magnon and photon modes.But in level attraction,a high-frequency incident photon emits a magnon and a photon simultaneously, reproducing a synchronizing variation of the generated magnon and photon.

Fig.2.(a)Temporal evolution of magnon(red)and photon(black)amplitudes of level repulsion for coherent coupling at resonance.The parameters used are a1 =a2 =1.0, g=0.1 and κc =κm =0.01.(b)Temporal evolution of level attraction for coherent coupling at resonance.In panel(b),κc=κm=0.11 is chosen to represent a weak coupling regime.Panel(c) is the same as panel (b) but outside the lock region.In panel (c),κc =κm =0.01 since the system outside the lock region is stable in the strong coupling regime.In panel(c),we choose the detuning Δmc=0.22.

5.Comparison to dissipative coupling

The level attraction studied in the previous section is mediated by the coherent and direct magnon-photon coupling.Besides the level attraction in coherent coupling,level attraction can be realized by dissipative coupling,which is mediated by the simultaneous coupling of magnon and photon with a common reservoir.[30]Such dissipative coupling has been observed in recent experiments.[24]The effective Hamiltonian of dissipative coupling is usually written as

There are some differences between the level attraction of coherent and dissipative couplings.First,the coupling mechanism is different as mentioned above.Second,the photon frequency is distinct.In the coherent coupling,it is in the range of visible light.But in the dissipative coupling,the microwave photon is used.

The dynamical equation of dissipatively-coupled Hamiltonian is written as

The eigenfrequencies and eigenstates are expressed by

As shown in Fig.1(c), the dissipative coupling presents the same spectrum as that of coherent coupling.But,the polarization of eigenstates is quite different from coherent coupling.At resonance, the hybridized states are of linear polarization.Inside the lock region, the polarization states evolve from elliptical polarization into the circular polarization at the EPs.Outside the lock region, they change gradually from elliptical polarizations to linear polarizations.Moreover,two eigenstates are orthogonal, which is different from non-orthogonal eigenstates in level attraction of coherent coupling.

Despite the different eigenstates, the temporal dynamics at resonance is similar to the level attraction of coherent coupling, e.g., a synchronizing variation of magnon and photon amplitudes.Here, one can discuss the connection between temporal dynamics and eigenstates.Based on Eq.(8), one can see that both eigenfrequencies and eigenvectors contribute to temporal dynamics.As two eigenvectors are orthogonal,eigenfrequency plays an important role.At resonance, two unequal eigenfrequencies result in the Rabi oscillation in coherent LR while the frequency merging in dissipative coupling leads to the synchronization.As two eigenvectors are nonorthogonal,both eigenfrequency and eigenvectors become dominant,giving rise to a synchronization for two modes with different frequencies in coherent LA.Physically, such synchronization is due to the simultaneous absorption and emission of two modes as described in the Hamiltonian Eq.(11).Moreover,the instability usually does not occur for dissipative coupling due to the presence of a reservoir in the magnonphoton coupling.The growth of magnon and photon amplitude will be suppressed greatly by the reservoir.

Finally, we would like to discuss the issue related to the experimental realization of our proposed theory and comparison with experimental works.As for experimental realization,the device of cavity optomagnonics has been realized in recent experiments.[33-36]These experiments provide evidences of coupling optical photons and ferromagnetic magnon.However, the temporal dynamics has not been studied.To do it, one needs to send microwave pulses to the system and then measure the decay behavior, which is different from the continuous-wave driving in previous experiments.[33-36]Our work provides insights into the eigenstates and temporal dynamics of cavity optomagnonics which will be helpful for future experiments.On the other hand, we will compare our work with a recent experimental work which studied the coherent and dissipative magnon-magnon coupling.[42]First,both our work and Ref.[42]revealed coherent and dissipative coupling.Second,our work studies the magnon-photon coupling while Ref.[42] studies the magnon-magnon coupling.Third,the coherent coupling in Ref.[42]is mediated by a cavity photon mode while the coherent coupling in our work is a direct magnetic dipolar interaction.

6.Conclusion

We study the eigenfrequency, eigenstates, and temporal dynamics for the coupling between ferromagnetic magnon and visible photon.In contrast to microwave photons,optical photons are coupled with magnon in a dispersive interaction which produces both level repulsion and attraction.The spectra,the polarizations of eigenstates,and especially temporal dynamics are analyzed for both red-detuned and blue-detuned regimes.At resonance, the hybridized states are of linear polarization and circular polarization for level repulsion and level attraction respectively.As the detuning increases,the polarizations of level repulsion remain unchanged but those of level attraction vary from elliptical to linear polarizations.The temporal dynamics of level repulsion presents the beat-like behavior.The level attraction presents monotonous decay in the weak coupling regime but gives rise to instability in the strong coupling regime due to the magnon amplification.As the detuning is large, both magnon and photon amplitudes present a synchronizing oscillation.Moreover,we compare the level attraction of coherent coupling to that of dissipative coupling.The eigenstates of dissipative coupling are linear polarization at resonance,elliptical polarization inside the lock region,circular polarization at the EPs and elliptical polarization and linear polarization outside the lock region.Although the eigenstates are quite distinct,the temporal dynamics are very similar for two types of level attractions.Our results are expected to be useful for future experimental studies in the field of pulsedriving experiments of cavity optomagnonics.

Acknowledgments

Project supported by the National Natural Science Foundation of China(Grant Nos.NSFC61974067 and 62374087).We thank Prof.Ke Xia and Prof.C.M.Hu for their helpful comments in doing this work.