Realization of high-fidelity and robust geometric gates with time-optimal control technique in superconducting quantum circuit
Zhimin Wang(王治旻), Zhuang Ma(马壮), Xiangmin Yu(喻祥敏), Wen Zheng(郑文),Kun Zhou(周坤), Yujia Zhang(张宇佳), Yu Zhang(张钰), Dong Lan(兰栋),Jie Zhao(赵杰), Xinsheng Tan(谭新生), Shaoxiong Li(李邵雄), and Yang Yu(于扬)
National Laboratory of Solid State Microstructures,School of Physics,Nanjing University,Nanjing 210093,China
Keywords: superconducting qubits,geometric quantum computation,time-optimal control
1.Introduction
Due to the advantages of potential quantum speeding up, quantum computation[1]has been widely considered a promising routine to solve some NP problems which cannot be processed effectively by traditional computers.Up to now, various physical systems have been proposed to realize quantum computation,such as nuclear magnetic resonance(NMR),[2]trapped ions,[3]quantum dots,[4]and superconducting circuits.[5]Among these candidate systems,superconducting qubit is one of the most promising routines implementing universal quantum computation.In the last two decades,many technological breakthroughs in superconducting qubits have occurred,[6-9]and the state of the art superconducting quantum processors have the ability to integrate tens of qubits and solve specific NP problems much faster than state-of-the-art supercomputers.[9,10]However, the imperfection of quantum gates is still one of the main limitations that hinders the scaleup of superconducting qubits.
Geometric quantum computation(GQC)offers a promising scheme to suppress errors induced by imperfect operations and decoherence.Quantum gates based on adiabatic geometric phases have been demonstrated,[11-13]which show robustness against operation errors.However, due to the speed limitation of the adiabatic condition, the decoherence effect induces more errors on adiabatic geometric gates than on dynamical ones.Thus some methods have been proposed to accelerate adiabatic geometric quantum gates and reduce errors caused by decoherence, which are based on both Abelian[14-18]and non-Abelian geometric phases.[19-21]Although these schemes have been demonstrated on various physical systems, the implementation is complicated because of the requirement of auxiliary energy levels.And the duration that a geometric gate takes is still longer than that of an equivalent dynamical gate.
Recently another scheme of nonadiabatic GQC utilizing the time-optimal control (TOC) technique[22]has been proposed to accelerate geometric quantum gates with smooth evolution paths.Instead of utilizing multiple waveforms to eliminate the dynamical phase,this scheme sets several restrictions to make the dynamical phase have geometric properties and reduce the sensitivity to noise.Meanwhile, the TOC technique is used to find the shortest geometric path of this nonadiabatic scheme.In addition,this scheme is easy to implement because it only utilizes the lowest two levels of each qubit.
In this paper, we experimentally implemented this nonadiabatic time-optimal GQC framework on a superconducting transmon qubit.This geometric scheme shows better robustness against control errors than the traditional dynamic gate while maintaining averaged fidelity above 99.80%.For the case of a universal single qubit gate, this scheme takes less time than the dynamical one under the same hardware limitation.Our work provides a promising candidate for scalable quantum computation.
2.Main text
First, we explain how to realize time-optimal geometric gates in a single qubit.The general Hamiltonian of a driven two-level system(as shown in Fig.1(a))in the frame rotating at qubit’s frequency can be expressed as
whereΩ(t)is the time-dependent driven Rabi frequency of the resonant microwave field,Φ(t)is the phase of the microwave field,Δ(t)is the detuning of frequency between the qubit and the microwave field.
Different from the traditional geometric phase of the cyclic path, the unconventional geometric phase used here arises from non-cyclic path.This geometric phase is proportional to the solid angle enclosed by the evolution path and the geodesic line between the initial point and the final point in the parameter space.[22]To eliminate the sensitivity of the dynamical phase against error,this scheme set a restriction on the evolution path to make the dynamical proportional to the geometric phase.[22]The time optimal control technique is used to find the Hamiltonian which implements the desired unitary operation in the shortest time,by solving the quantum brachistochrone equation.[22,23]After the acceleration,TOC geometric gate is executed much faster than traditional nonadiabatic geometric gates.[22]
To implement a TOC geometric gate,a rotation aroundXaxis andYaxis are done by a driving field
whereΦ0is the phase of the driving field.In our experimentΦ0=-π/2 corresponds toRxrotation andΦ0=0 corresponds toRyrotation,θis the amplitude(ampl.) of rotation.For example,Φ0=-π/2,θ=πcorresponds toXgate.For demonstration,the time-dependent Hamiltonian of the TOCXgate is shown in Fig.1(b), while the corresponding evolution path of the qubits state is shown in Fig.1(c), which moves from B to D on the Bloch sphere.
In this scheme,the envelope of the driven field can be cosine function or sine function, and the simulation shows that the results of them are equivalent.TheσZterm of the Hamiltonian is realized by adding a fixed detuning between the frequencies of the qubit and driven microwave.TheσXandσYterms are realized by modulating the amplitude and phase of the microwave field.
We implement this experiment on a quantum processor which consists of six transmon qubits.Only one of these qubits (Q1) is used in our experiment.The layout of the qubit and the diagram of the measurement system are shown in Fig.1(e).The cross capacitor in the center of this microphoto is the shunt capacitor of the Xmon qubit,and the frequency of this qubit was set at 5.844 GHz during our experiment.TheXYcontrol line on the left capacitively couples to the qubit.On the right side, there is a capacitively coupledλ/4 coplanar waveguide resonator for qubit readout.The resonator frequency is 6.935 GHz.The measured relaxation timeT1of this qubit is 27 µs and the decoherence timeT2is 12 µs.In this experiment, we neglected higher energy levels above the first excited state,since the anharmonicity of this qubit is large enough(-274 MHz).
The benefit of the acceleration in the TOC scheme is shown in Fig.1(d).Here we set the maximum driven field as 20 MHz and compare the time duration of the TOC scheme with that of the conventional geometric scheme.For fairness,the envelope of the driven field is chosen as a sine function for both schemes.We can see that the TOC gates take less time than the equivalent conventional geometric gates,and this advantage is more significant in small-angle rotations since this scheme is noncyclic.Then the corresponding upper bounds of fidelities limited by decoherence are estimated by the formula from Ref.[24]while the decoherence parameters are the same as above.

Fig.2.Quantum state tomography for TOC geometric gates which include X, X/2,Y,Y/2 gates.The initial states are all prepared in the ground state|0〉.Solid lines correspond to the results of the simulation,and the dots correspond to the experimental data.(a)-(d) The expectation values of Pauli operators.Here weuse different co〈lors〉(green,red,andpurple)torepresent different expectation values:〈σx〉,σy,〈σz〉.(e) and(f) Trajectories of X and Y (X/2 and Y/2)gates on the Bloch sphere.The red dots are the results of the X-axis rotation while the green ones are those of the Y-axis rotation.
We perform state tomography to characterize the evolution of the quantum state during the geometric manipulation,while the state of the qubit was prepared at|0〉 initially.The expectation values of three Pauli operatorsσx,σy,σzare displayed in Figs.2(a)-2(d), and these four graphs are the results of geometricX,X/2,Y,Y/2 gates respectively.In all these experiments, the evolution time of the geometric gates is set to 30 ns.These evolution trajectories of quantum states are demonstrated on Bloch sphere (Figs.2(e) and 2(f)).In Fig.2, the solid lines correspond to the results of the simulation by numerically calculating the master equation,while the dots correspond to the experimental data.We can see that the experimental results agree very well with the simulation.
To benchmark the fidelity of TOC geometric gates, the Clifford-based randomized benchmarking (RB) technique[25]is utilized.The results of RB are shown in Fig.3.By changing the length of the random sequence and measuring the residual population in|0〉,we can get an exponentially decaying curve that fits withP=Apm+B, wherePis the population of the ground state,pis the depolarizing factor which is related to the fidelity,AandBparameters are relevant to the readout of the qubit.By fitting the parameters of the reference curve(Pref)and interleaved curve(Pgate),we can get the fidelity of the interleaved gate by
whered= 2 in our case of a single qubit.The fidelities ofRx(π) andRx(π/2) TOC geometric gates are 99.81% and 99.79%respectively.In addition,we also simulate these fidelities by solving the master equation and take the decoherence and the qubits anharmonicity into consideration.By using the standard process tomography method,the simulated fidelities ofRx(π)gate~99.76%andRx(π/2)gate~99.83%are obtained.According to the formula proposed by Ref.[24], the upper limit of fidelity is 99.86%, which is calculated by the duration of the gate and the decoherence timeT1,Tφ.We can infer that the main error of the geometric gates originates from the decoherence of the qubit.
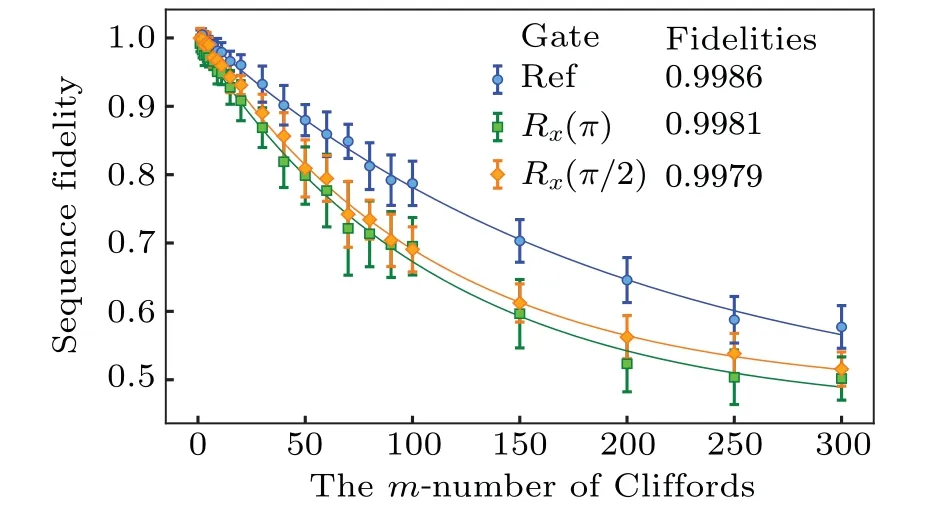
Fig.3.Standard randomized benchmarking(RB)results of TOC geometric gates.The blue curve is the result of reference RB,while the others are the results of interleaved RB.The sequence fidelity of each curve decays as a function of the number of Clliford gates.By fitting the decay rate, we can get that the fidelities of X gate and X/2 gate are 99.81% and 99.79% respectively,while the average fidelity of the reference is 99.86%.Each curve is averaged from 20 independent repeats, while error bars demonstrate the standard deviations calculated from those repeats.
To examine the robustness against control error of the time-optimal geometric gates, the standard quantum process tomography[26,27]is used to measure the fidelities of the geometric gates and dynamical gates.The fidelity of a quantum process is obtained by
Hereχexpis theχmatrix of the quantum process rebuilt by experiment, whileχidis calculated by theoretically applying process tomography to the corresponding perfect gate.To get theχexp, the process tomography sequences were executed as follows: we initialize the qubit by four different operations:{I,X/2,Y/2,X}, next apply the targeted gate to the qubit,then the four final states are obtained by quantum state tomography.[1]The density matrices of the four initial states are calculated theoretically.After we obtain the density matrices of all these initial states and final states,we can reconstruct the process matrixχexpby quantum process tomography,then the fidelities of the target gates can be calculated by Eq.(3).To compare the robustness of TOC geometric gates and conventional Rabi-based dynamical gates, we intentionally add relative amplitude errorδA/ΩMand detuning errorδΔ/ΩMto our control pulse.In practical, these errors may occur in the case that the system parameters are not well calibrated or spectator qubits shift the parameters of the operating qubit due to residual qubit-qubit coupling.Here we characterize the robustness ofRy(π)gate[Figs.4(a)and 4(b)]andRy(π/2)gate[Figs.4(c) and 4(d)] against amplitude error [Figs.4(a) and 4(c)] and detuning error [Figs.4(b) and 4(d)] of the control pulse.We vary each kind of error from-0.3 to 0.3 and repeat the process tomography to measure the fidelities of both geometric gates and dynamical gates.As shown in Fig.4,the fidelity of the TOC geometric gate declines much slower than that of the corresponding dynamical gate while the control error increases, thus TOC geometric gates show better robustness than dynamical ones,and this advantage is more obvious in the case of detuning error than that in the case of amplitude error.The robustness of TOC geometric gates comes from their natural geometric feature,which reduces their sensitivity to errors that originate from imperfect control or environmental noise.
This scheme is also applicable for nontrivial two-qubit geometric gate.The similar scheme for entangled gates can be realized by utilizing the interactions of the singleexcitation subspace{|01〉,|10〉}.By using parametric modulation,the coupled Hamiltonian in the{|01〉,|10〉}subspace[22]and equation (1) are similar in form, we can implement nontrivial two-qubit geometric gates by modulating the amplitude,frequency,and phase of the longitudinal driving field.
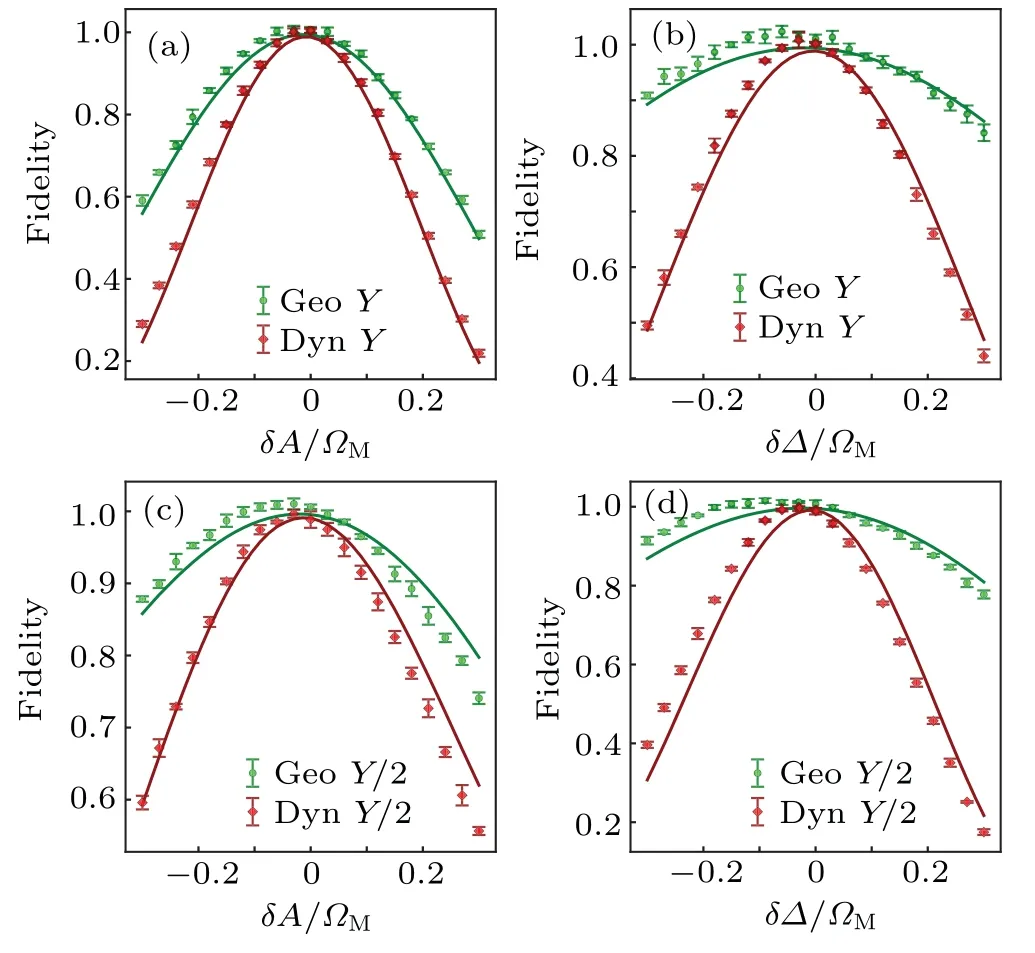
Fig.4.Gate performance of TOC geometric gates and dynamical gates as a function of control error.The green dots and green solid lines are the experimental fidelities and simulated fidelities of TOC gates respectively, while the red dots and red solid lines correspond to those of dynamical gates.Here we characterize the robustness of Y gate[(a)and(b)]and Y/2 gate[(c)and(d)]against relative amplitude error δA/ΩM[(a)and(c)]and detuning error δΔ/ΩM [(b)and(d)].We can see that TOC geometric gates perform better than traditional dynamical gates when the amplitude error or the detuning error exists.The advantage is larger in the case of detuning error than that in the case of amplitude error.
3.Conclusion
In conclusion,we experimentally demonstrate the scheme of time-optimal geometric gates on a single superconducting qubit and obtain the averaged fidelity above 99.8%for singlequbit gates.Moreover,these geometric gates reveal better robustness against amplitude error and detuning error than dynamical gates.In this scheme, the most important improvement is that the geometric gates can be accelerated by the timeoptimal control technique and take less time than traditional geometric gates.
Acknowledgements
Project supported by the Key Research and Development Program of Guangdong Province, China (Grant No.2018B030326001),the National Natural Science Foundation of China(Grant Nos.11474152,12074179,U21A20436,and 61521001),and the Natural Science Foundation of Jiangsu Province,China(Grant No.BE2021015-1).
- Chinese Physics B的其它文章
- Corrigendum to“Reactive oxygen species in plasma against E.coli cells survival rate”
- Dynamic decision and its complex dynamics analysis of low-carbon supply chain considering risk-aversion under carbon tax policy
- Fully relativistic many-body perturbation energies,transition properties,and lifetimes of lithium-like iron Fe XXIV
- Measurement of the relative neutron sensitivity curve of a LaBr3(Ce)scintillator based on the CSNS Back-n white neutron source
- Kinesin-microtubule interaction reveals the mechanism of kinesin-1 for discriminating the binding site on microtubule
- Multilevel optoelectronic hybrid memory based on N-doped Ge2Sb2Te5 film with low resistance drift and ultrafast speed

