Defogging computational ghost imaging via eliminating photon number fluctuation and a cycle generative adversarial network

Yuge Li(李玉格) and Deyang Duan(段德洋)

School of Physics and Physical Engineering,Qufu Normal University,Qufu 273165,China

Keywords: computational ghost imaging, image defogging, photon number fluctuation, cycle generative adversarial network

1.Introduction

Due to existence of fog, outdoor images usually suffer from low contrast and limited visibility, which adversely affects performance of computer vision tasks, such as object detection and recognition.Consequently, more attention is needed to recover clean image from a hazy input.Early methods tried to estimate the transmission map by using physical priors and then restoring the image via the McCartney scattering model.[1]However,these physical priors are not always reliable, leading to inaccurate transmission estimates and unsatisfactory dehazing results.Recently, many methods based on deep learning have been proposed to overcome drawbacks of using physical priors.[2-4]Most learning-based methods are trained on synthetic data.Unfortunately, it is almost impossible to obtain hazy/clean image pairs from the real world.Consequently, dehazing models trained on synthetic images usually generalize poorly to real-world hazy images.

Ghost imaging techniques appear to provide a promising way to obtain defogging images.Previous works show that the scattering media has little effect on ghost imaging when the scattering media is located in the position between the object and the bucket detector.[5-8]However,no matter whether liquid or solid scattering media are employed,when the media are evenly distributed in the optical path,they will have serious impacts on ghost imaging.[9-12]Recall that the conventional McCartney model regards scattering media including fog as a medium with space-time invariance.However,ghost imaging technique requires a lot of measurement data to reconstruct the image of the object, which is different from the conventional optical imaging although some methods have greatly reduced the required samples.[13-16]In the process of data sampling,the influence of fog fluctuation on the light cannot be ignored.Consequently,it is inappropriate to assume that the fluctuating fog is space-time invariant.The scattering and absorption of fluctuating fog will lead to the photon number fluctuations on the detection plane in different measurement events.The relationship between photon number fluctuations and ghost image degradation will be investigated based on photon statistics and the McCartney model in this paper.Then, our purpose is to obtain a high-quality defogging ghost image.

2.Theory

Before the following analysis,we make two agreements:(i) We adopt the statistical view of light, i.e., point sources of radiation emit photons,or subfields,randomly in all possible directions.(ii) Fog has random fluctuation.Figure 1 is a conventional computational ghost imaging setup, except that fog is evenly distributed in the optical path.A monochromatic light-emitting-diode (LED) illuminates a spatial light modulator (SLM).Then, the modulated light illuminates an object after propagating throughlmeter without fog.Finally,the reflected light carrying the object’s information is collected by a bucket detector after propagating throughdmeters of the fog medium.The signal measured by the bucket detector can be expressed as[17]

wherenrepresentsn-th measurement event,ρrepresents the transverse coordinate,gis Green’s function for propagation from the object to the bucket detector.T(ρ) is the function of the object.V(q)is the modulated function of SLM,which follows Gaussian statistics,whereqis the wave vector.[18]Emis expressed as[19]

wheremrepresents them-th subfield,γrepresents the scattering coefficient,correspondingly,γdis the optical path.We model the radiation source as a collection of a large number of independent and randomly radiating point-like subsources randomly distributed on a disk parallel to the object plane.[17]The first term on the right-hand side of Eq.(2) represents the scattering light,while the second term represents the ambient light.Obviously,the measured light field has significant photon number fluctuations introduced by fog,which leads to the image blurring.The calculated light can be obtained by the diffraction principle of light as follows:

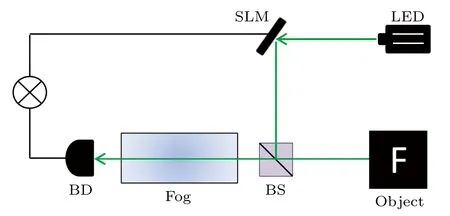
Fig.1.Setup of computational ghost imaging through fog.SLM:spatial light modulator,BS:beam splitter,BD:bucket detector.

We introduce an algorithm to eliminate the photon number fluctuation.A software records the registration time of each photodetection event for the real light detected by the bucket detector and the the calculated light detected by the virtual detector.It accomplishes this by using two independent yet synchronized event timers along their time axes which are divided into sequences of short time windows.Then,the software calculates the average counting numbers per short time window,and.Subsequently, the software classifies the counting numbers per window as positive and negative fluctuations based onand,i.e.,

wherei=1,2 andj=1 toMare used to label thej-th short time window, andMis the total number of time windows.Then,we define the following quantities for the statistical correlation calculations of

Thus,the corresponding statistical average of〈Δn1Δn2〉is

3.Results

To simplify the simulation, we assume that the fog consists of 100% water.Thus, the light fluctuation on the image plane is related to the fluctuation of particle size and thickness.Here,the pixel size of the SLM is set to 15µm×15µm,and the spatial distance of the fog environment is set to 10 m.

Fig.2.Upper: Simulated fog with fluctuation.Lower: Experimentally measured fog with fluctuation.

Fig.3.Upper: Influence of fog particle size fluctuation on computational ghost imaging.The diameters of fog particles are (a1) 20 µm,(a2)30µm,(a3)40µm,and(a4)50µm.Lower: The defogging ghost images reconstructed by our method.

Figure 2 presents the fog fluctuations for the simulation and experiment in different measurement events.Figure 3 shows the effect of fog particle size fluctuations on computational ghost imaging with 20000 measurements.Obviously,the fluctuations of fog particle size will cause the photon number fluctuations on the detection plane,resulting in image blurring.Clear images are reconstructed by eliminating the photon number fluctuation.Indeed, the quality of the reconstructed image is almost the same as that of the object inserted in Fig.1.Figure 4 shows the effect of fog thickness fluctuations on computational ghost imaging.Similarly, high-quality images can be obtained by this method too.To quantitatively evaluate the effect of this method,the structural similarity(SSIM)and peak signal-to-noise ratio (PSNR) are used to measure the image quality(Fig.5).

Fig.4.Upper: Influence of fog thickness fluctuation on computational ghost imaging.The thickness of fog is defined as 0-10.The diameter of the fog particle is set to 30µm.Lower: The reconstructed defogging ghost images.

Fig.5.The SSIM(a)and PSNR(b)curves of the blurred images with fog (BIF) and reconstructed photon number fluctuation defogging images(PNFDI).

The experimental setup of computational ghost imaging through fog is shown in Fig.1.An LED illuminates the surface of a two-dimensional amplitude-only ferroelectric liquid crystal spatial light modulator(Meadowlark Optics A512-450-850)with 512×512 addressable 15µm×15µm pixels.The modulated light illuminates an object and its reflected light is detected by a bucket detector.The length of the fog generating device isd=0.6 m.The experimental results are shown that our method has amazing defogging effect,especially for practical objects (Fig.6).The corresponding quantitative results are shown in Fig.7.These results (Figs.3, 4, and 6) confirmed that the photon number fluctuation is indeed the reason of ghost image degradation.

Although a high-quality ghost image has been obtained by eliminating photon number fluctuation,there are still some differences between a defogging ghost image and the image without fog, e.g., low brightness.We use a cycle generative adversarial network (CycleGAN)[20]to further eliminate the influence of fog on computational ghost imaging.The setup of CycleGAN is illustrated in Fig.8.CycleGAN contains two mapping functions (G:X →Y,F:Y →X) and their corresponding discriminators(DYandDX),whereXandYare the original and the target domains,respectively;andGandFare generators ofXtoYandYtoXmappings,respectively.

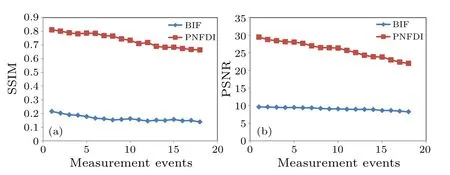
Fig.7.The SSIM (a) and PSNR (b) curves of experimental blurred images(BIF)and reconstructed images(PNFDI)with practical object.

For the mapping function (G:X →Y) and its discriminator(DY),the countermeasure loss function can be expressed as

wherePdata(x)andPdata(y)represent the sample distribution in theXdomain and the sample distribution in theYdomain,respectively.The generatorGattempts to make the generated imageG(x)as similar to they-domain image as possible.However,the discriminator dy distinguishes the generated imageG(x) from the real imageyas much as possible.Consequently, we obtain minGmaxD(Y)LGAN(G,DY,X,Y).For the mapping function (F:Y →X) and its discriminatorDX,we have minFmaxD(X)LGAN(F,DX,Y,X).We introduce the cycle-consistent loss function to preserve the image information when converting between image domains.Here,for each imagexin theXdomain, the cyclic conversion of the image can restorexto the original image, i.e.,x →G(x)→F(G(x))≈x, which is called the forward cyclic consistency loss[Fig.8(b)].Similarly,for each imageyin theYdomain,GandFsatisfy the consistent loss of the reverse cycle[Fig.8(c)],i.e.,y →F(y)→G(F(y))≈y.Thus,the cycle-consistent loss function can be expressed as

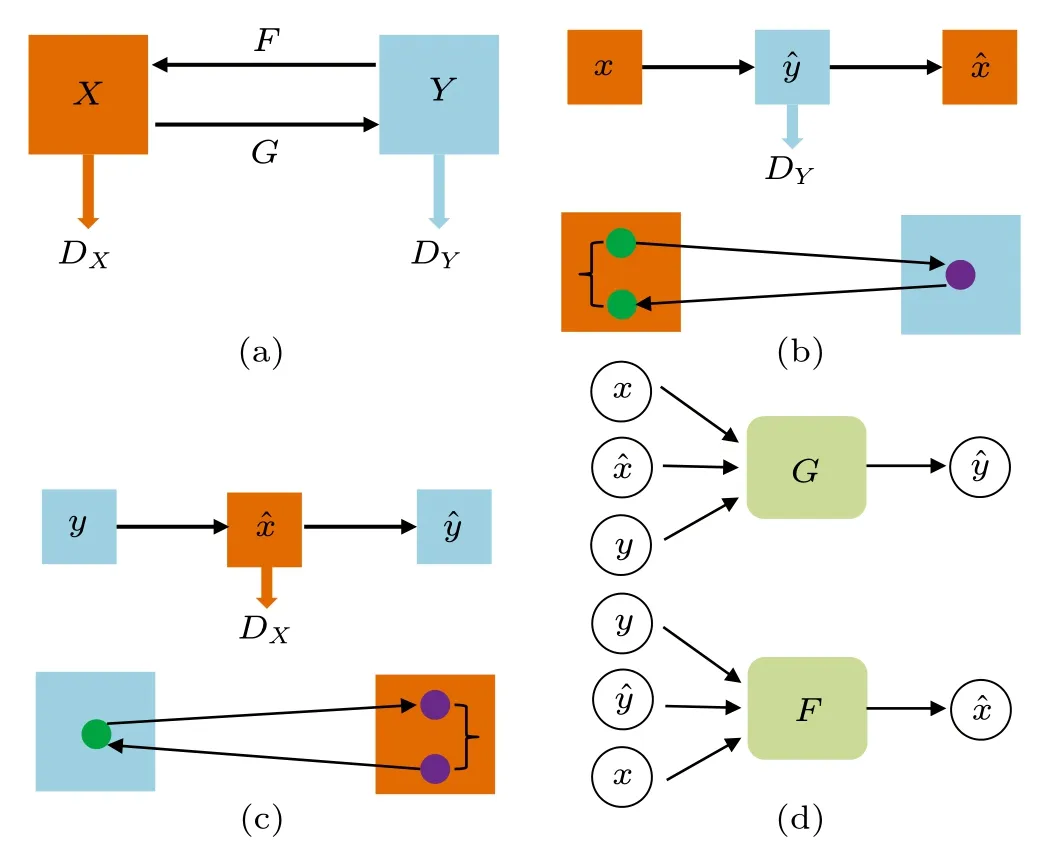
Fig.8.The network structure of the CycleGAN:(a)mapping function of CycleGAN,(b)forward circulation consistent loss,(c)reverse circulation consistent loss,(d)generators of CycleGAN.

In CycleGAN,mappingG:X →Yrepresents that generatorgconverts images in theXdomain to theYdomain.If generatorGinputs an imageyin theYdomain, we can obtainG(y)=y.Consequently,we add an identity map to these two generators to achieve this function, i.e.,G:y →yandF:x →x.Thus, the inputs of generatorsGandFincludex,x,y, andy,y, andX, respectively (Fig.9).The loss in this mapping is called the identity loss,i.e.,

The loss function of the CyeleGAN network can be expressed as

whereηandµrepresent the weight parameters of cycle consistency loss and feature loss,respectively.

Fig.9.Top: fog images.Middle: the reconstructed images via eliminating photon number fluctuation and CycleGAN.Bottom: the reconstructed images via CycleGAN.

Fig.10.The SSIM (a) and PSNR (b) curves of blurred images (BIF),and the reconstructed images via CycleGAN (CGAN-C), the reconstructed images via eliminating photon number fluctuation (PNFDI),and the reconstructed images via eliminating photon number fluctuation and CycleGAN(CGAN-P).

In the experiment, the dataset is divided into training set and a test set.The training set consists of trainaand trainb,where trainastores 50 images with fog and trainbstores 50 images without fog.The experiment used the Adam optimizer with batch size of 1.The network iterates 200 epochs.In the first 100 epochs,the learning rate of the network remains unchanged at 0.0002,and in the last 100 epochs,the learning rate decays linearly to 0.Hereη=10,µ=0.5.The deep learning framework is Pytoch 1.4.0, and the interpreter is Python 3.6.Quantitative results are presented in Fig.9.The images reconstructed by eliminating photon number fluctuation and CycleGAN are almost the same as those without fog,which is far better than those solely reconstructed by CycleGAN.

4.Conclusion

In summary, we have theoretically and experimentally demonstrated that the photon number fluctuation introduced by fluctuating fog is the reason for ghost image degradation.Then, an algorithm is used to process the measurement events to obtain the signals without photon number fluctuations.Thus, a high-quality defogging ghost image is reconstructed, even if the fog is evenly distributed in the optical path.This method, without any physical priors or synthetic data, is effective regardless of the concentration of fog.Finally,image processing methods are still indispensable to obtain nearly 100%fog-free images.

Acknowledgement

This work was supported by the Natural Science Foundation of Shandong Province, China (Grant No.ZR2022MF249).