First-principles study of moderate phonon-mediated pairing in high-pressure monoclinic phase of BiS2-based superconductors
Jie Cheng(程杰), Yu-Lan Cheng(程玉兰), Bin Li(李斌), and Sheng-Li Liu(刘胜利)
1School of Science,New Energy Technology Engineering Laboratory of Jiangsu Province,Nanjing University of Posts and Telecommunications,Nanjing 210023,China
2College of Electronic and Optical Engineering&College of Flexible Electronics(Future Technology),Nanjing University of Posts and Telecommunications,Nanjing,210023,China
Keywords: BiS2-based superconductor,high pressure,isotope effect,phonon-mediated pairing
1.Introduction
Superconductivity in layered crystal structure such as cuprates,[1]iron-pnictides,[2]and MgB2,[3]has aroused enormous research interest.A new family of layered BiS2-based system has triggered off another wave of extensive studies since its discovery in 2012.As the first member, the compound of Bi4O4S3was reported,[4]then theReOBiS2- (Re:rare earth),[5-9]SrFBiS2-,[10]ReOMS2(M=Sb and In)-,[11,12]and La2O2M4S6(M=Pb,Bi,Ag)-type superconductors[13-15]have been discovered successively.Here, the basic structural unit of BiS2-based compounds is the BiS2layer,which is analogous to the Cu-O planes in cuprates and the Fe-A(A=P,As,Se,Te)planes in iron-pnictides.[1,16]Of these BiS2-based compounds,theReOBiS2-type is mostly studied owing to their simple structure and easy carrier doping control.For example,in LaO1-xFxBiS2,the partial substitutions of F-for O2-sites generate electron carriers, and the maximum transition temperature (Tc) is observed to be 2.5 K whenx=0.5 at ambient pressure.[17]Interestingly, by applying external pressure,Tcabruptly increases to a maximal value of 10.7 K, which is caused by the structural phase transition from tetragonal phase(P4/nmm, ambient-pressure) to monoclinic phase (P21/m,high-pressure).[18]Moreover,band structure calculations indicate the presence of strong Fermi surface nesting at the wave vector (π,π), which is the hallmark of iron-pnictides.[19,20]Therefore,the superconducting mechanism in BiS2-based system may be expected to resemble that of iron-pnictides, although the mechanism of superconductivity in iron-pnictides is still in dispute.
According to the Bardeen-Cooper-Schrieffer (BCS)theory,[21]theTcof a phonon-mediated conventional superconductor is proportional to its phonon frequency, and it is very sensitive to the isotope mass (M) of the constituent elements.This is the so-called isotope effect.Furthermore,the relationship betweenTcand isotope mass satisfiesTc~M-α,[22]in whichαis the isotope exponent, andα~0.5 is expected according to BCS theory.Therefore,the isotope effect can be considered as an essential indicator to investigate whether the mechanism of superconductors is conventional.For instance,αhas been reported to be~0.5 for the conventional superconductors, such as (Ba,K)BiO3(αO~0.5),[23]doped fullerene (αC~0.5),[24]and MgB2(αB~0.3).[25]In high-Tcsuperconductors with unconventional mechanisms,αgenerally deviates from 0.5(e.g.near-zeroαOin cuprates,[26]and even negativeαFein iron-pnictides[27]).
For this new BiS2-based system, the fundamental question is whether the superconductivity can be understood within a conventional electron-phonon coupling framework.Hence,several investigations concerning the isotope effect of BiS2-based compounds have been proposed.By replacing S element in Bi4O4S3with32S and34S, the isotope exponentαSis estimated to be in a range:-0.1<αS<0.1.[28]A similar unconventional isotope effect is also observed in LaO0.6F0.4BiSSe with BiSSe-type superconducting layers, in which the change ofTcbetween the76Se sample and80Se sample is apparently smaller than that expected from the photon-mediated mechanism.[29]Very recently, Yamashitaet al.pointed out that under high pressure, the superconducting mechanism can be transformed from unconventional to conventional one by breaking the structural symmetry in superconducting BiS2layers.[30]It should be noted that these above-mentioned results of unconventional superconducting mechanism are based on the low-Tctetragonal structures at ambient-pressure.Therefore, it is highly desirable to investigate the isotope effect on the high-pressure monoclinic phase,which may present an important clue to the understanding of the pairing mechanism in BiS2-based superconductors.
In this work, we perform first-principles phonon calculations for the high-pressure monoclinic structure of LaO0.5F0.5BiS2.The changes inTcbetween32S sample and34S sample are observed,furthermore,the corresponding isotope exponent of 0.13≤α ≤0.20 is obtained.These findings prompt the high-pressure structure of LaO0.5F0.5BiS2to be a moderate phonon-mediated superconductor, which is quite different from the unconventional isotope effect of ambientpressure phase.
2.Computational method
The lattice data of LaO0.5F0.5BiS2were constructed by Materials Studio software.Starting from the initial lattice parameters, we performed the full structural optimization including both the lattice parameters and atomic positions.Phonon calculations were carried out by using density functional perturbation theory (DFPT) method via QUANTUM ESPRESSO program and a standard solid-state pseudopotential (SSSP).[31-33]The exchange-correlation energy was described by the Perdew-Burke-Ernzerhof (PBE) functional based on generalized gradient approximation (GGA).[34]For self-consistent calculation,8×8×8k-point grid was used with an energy cutoff of 30 Ry (1 Ry=13.6056923 eV) for the wave function and 300 Ry for the charge density.Dynamical matrices and electron-phonon coupling were calculated on a 4×4×4q-point mesh.Then,a dense 24×24×24 grid was used for evaluating an accurate electron-phonon interaction matrix.
3.Results and discussion
Crystal structures of LaO0.5F0.5BiS2for ambientpressure tetragonal and high-pressure monoclinic phases are cited from Ref.[35] (a= 4.1091 °A,c= 13.4196 °A) and Ref.[18] (a= 4.042 °A,b= 4.059 °A,c= 12.809 °A,β=97.31°),respectively.Here,half of the O sites are replaced by F,serving as the electron doping.Without such a replacement,the ambient-pressure structure and high-pressure structure belong to the space groupsP4/nmmandP21/m, respectively.The optimized results are summarized in Table 1, together with available experimental data.For the ambient-pressure tetragonal phase, the calculated structures coincide well with experimental results.However, there is a large difference between the calculation results and experimental data for highpressure phase,which can be attributed to an obvious contrast between the pressure application of calculated (18 GPa) and experimental conditions(4 GPa).
Figure 1 shows the calculated phonon dispersions and partial phonon density of states (PDOS) for LaO0.5F0.5BiS2in tetragonal phase at 0 GPa, in which 30 phonon bands are extended to 430 cm-1.A striking feature of this phonon spectrum is the presence of phonon softening along theAMdirection, indicating that the ambient-pressure structure of LaO0.5F0.5BiS2is dynamically unstable.Note that the soft phonon found here is an intrinsic property of the BiS2plane in tetragonal phase.[36]It is clearly seen from the PDOS that these unstable modes are directly traceable to the inplane vibrations of S atoms,which is consistent with previous report.[37]Moreover, unstable phonon modes are intimately associated with a charge density wave instability,and conventional phonon-mediated pairing cannot explain the superconductivity of LaO0.5F0.5BiS2in the tetragonal phase.[38]
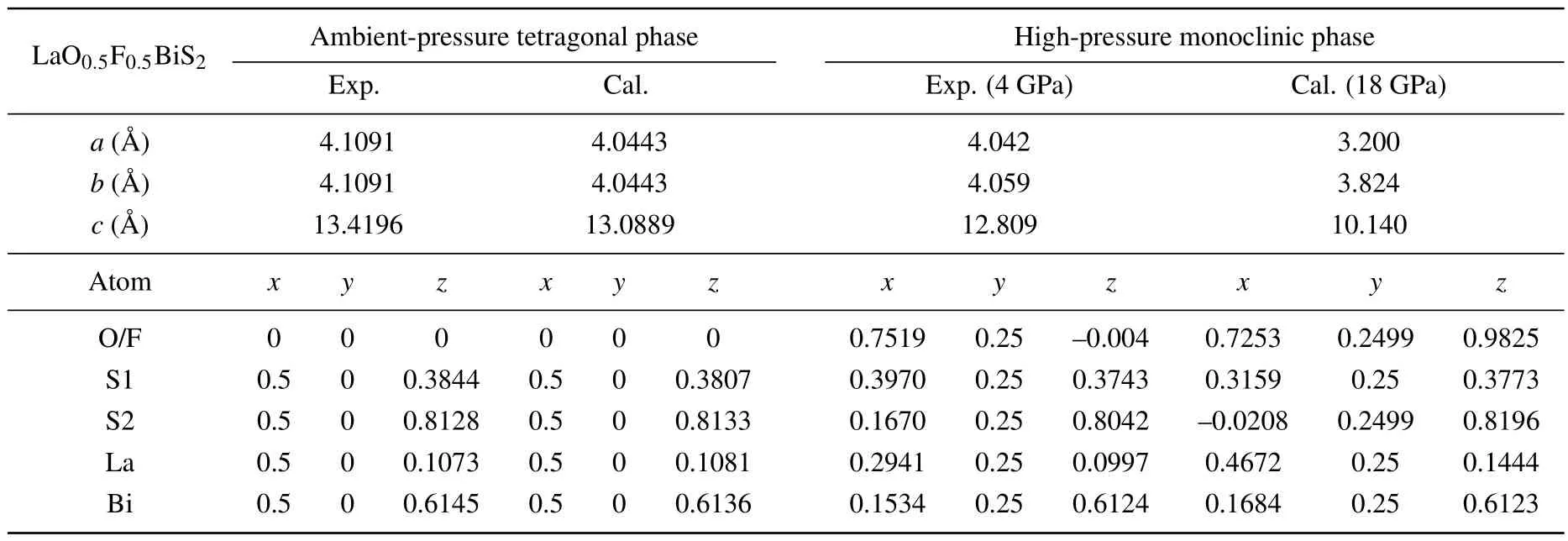
Table 1.Calculated lattice parameters and atomic positions of LaO0.5F0.5BiS2 for ambient-and high-pressure phases, with related experimental results listed for comparisons.
For the high-pressure monoclinic structure of LaO0.5F0.5BiS2, we carry out the phonon calculations in a pressure range from 12 GPa to 18 GPa.The corresponding phonon dispersion curves and PDOS curves at 18 GPa are plotted in Fig.2(a).There is no imaginary frequency in both phonon spectra, suggesting the dynamic stabilization of high-pressure phase.As seen from the phonon dispersion,the frequency extends to 700 cm-1, and it can be divided into two parts.The first part is the low-frequency band, with the phonon frequency ranging from 0 cm-1to 300 cm-1,mainly caused by the vibrations of La and Bi atoms, while the highfrequency bands(340 cm-1-700 cm-1)mostly originate from the contributions of S, F, and O atoms.It is well understood that S, F, and O atoms with lighter mass usually have higher vibration frequency than Bi and La atoms.In addition, we provide a further analysis of each phonon band at theΓpoint.The point group atΓpoint is C1, and theΓ-point mode can be decomposed asΓ= 30 A.The detailed frequencies are listed in Table 2,with the three acoustical branches excluded.Furthermore, in Fig.2(b), we give the atom vibration pattern of several typical phonon bands atΓpoint, whose frequencies are 181.9 cm-1(A8mode),477.4 cm-1(A18mode),and 569.8 cm-1(A26mode), corresponding to the three colored lines from bottom to top in Fig.2(a).The A8mode corresponds to the in-plane stretching vibrations with motion along thex(y)axis.In the A18mode,the O,F,and S2atoms vibrate along the samezdirection,opposite to the vibration direction of S1atoms,while the A26mode corresponds to the vibration of only O atom and S2atom.
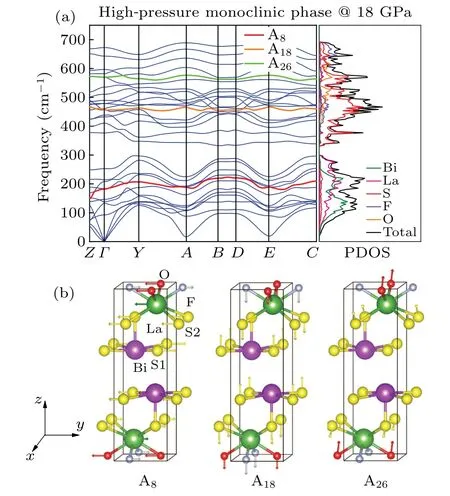
Fig.2.(a)Phonon dispersion and projected PDOS for LaO0.5F0.5BiS2 in high-pressure monoclinic phase at 18 GPa.(b) Atom vibration pattern of typical A8,A18,and A26 modes at Γ point.

Table 2.Phonon mode frequencies(in unit cm-1)at Γ point for LaO0.5F0.5BiS2 in high-pressure monoclinic phase,with I denoting infrared active,and R representing Raman active.
To investigate the isotope effect of LaO0.5F0.5BiS2in high-pressure monoclinic phase, we perform the substitution of S element.Then the LaO0.5F0.5BiS2samples with32S and34S isotopes are obtained,labeled as32S sample and34S sample, respectively.The effect of electron-phonon coupling on conventional superconductivity can be well represented by the Eliashberg function[39]
Here,N(EF) is the density of states at the Fermi level,ωis the frequency,nandn'run over electronic band,vover phononic band,kandqover the Brillouin zone.The electronphonon matrix elementis defined by the variation in the self-consistent crystal potential.Integrating the Eliashberg function over frequency,we can get the electron-phonon coupling factorλas follows:
The characteristic phonon frequencyωlnis defined as
For LaO0.5F0.5BiS2in high-pressure phase with32S sample and34S sample, figure 3 shows the Eliashberg functionα2F(ω)and electron-phonon couplingλ(ω)at 18 GPa.Combining with the PDOS in Fig.2, it can be clearly found that the electron-phonon interaction of Bi-S bond plays a crucial role in enhancing the value ofα2F(ω).Accordingly,the difference ofα2F(ω) between32S sample and34S sample is mainly reflected the in high-frequency region, showing a small red-shift with the increase of isotope mass of S element.Under the pressure application of 18 GPa, both32S sample and34S sample have a factorλ=0.61, suggesting that the LaO0.5F0.5BiS2in high-pressure phase is a moderately coupled electron-phonon superconductor.The values of electronphonon coupling factorλand the characteristic phonon frequencyωlnfor32S sample and34S samples in a pressure range of 12 GPa-18 GPa are listed in Table 3.For the32S sample at 12 GPa, the value ofλis about 0.40, with the logarithmically averaged frequencyωln=271.3 K.With the increase of pressure, theλmonotonically increases, accompanied by the decrease ofωln.In addition, the isotope substitution of S element has little influence onλ, but the values ofωlnin34S samples are generally smaller than those of32S ones.For instance,theωlnof32S sample at 13 GPa is about 274.0 K,while it decreases to 271.4 K for34S sample.
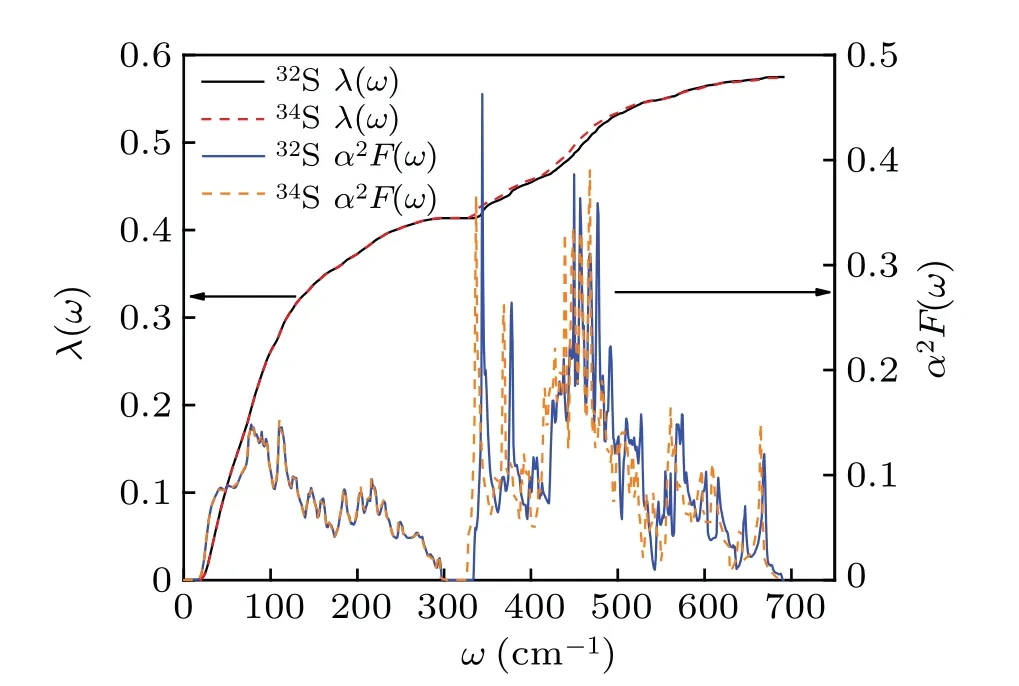
Fig.3.Eliashberg function α2F(ω) and electron-phonon coupling λ(ω) for LaO0.5F0.5BiS2 in high-pressure phase with 32S sample and 34S sample at 18 GPa.

Table 3.Values of electron-phonon coupling factor λ,characteristic phonon frequency ωln,and superconductive transition temperature Tc for LaO0.5F0.5BiS2 in high-pressure phase with 32S sample and 34S sample in a pressure range of 12 GPa-18 GPa.
The effect of electron-phonon coupling onTcis well quantified by the McMillan-Allen-Dynes formula as follows:[40]
whereµ∗is a pseudopotential parameter that represents the effective electron-electron mutual Coulomb repulsion suppressing pairing instability, and hereµ∗= 0.1.We further analyze the isotope effect ofTcby using the isotope coefficientα,which is given by
in which[M]32Sand[M]34Sare the atomic mass of32S and34S isotopes,respectively.
The calculatedTcof LaO0.5F0.5BiS2in high-pressure phase for32S sample and34S sample under the pressure in a range of 12 GPa-18 GPa is displayed in Table 3.Comparing with the34S sample, theTcof32S sample is high,which is in agreement with the isotope effect.However, the calculatedTcof LaO0.5F0.5BiS2in high-pressure phase is always lower than the experimental value,for example,the calculatedTcof32S sample at 18 GPa is 4.0 K, while its experimental one is 5.5 K.[18]Based on the changes ofTcbetween32S sample and34S sample, the isotope coefficient is exhibited in Fig.4.It is found that the isotope coefficient of LaO0.5F0.5BiS2in high-pressure monoclinic phase is estimated to be 0.13≤α ≤0.20,which is much greater than that of ambient-pressure phase, and slightly smaller than that of conventional MgB2(i.e.0.30).[25]We thus conclude that the moderate electron-phonon coupling has a vital role in determining the superconductivity of high-pressure phase.Moreover, taking into account the calculatedTclower than experimental value,cooperative multiple pairing mechanism should be also considered,such as electron-electron correlation.[41,42]Recalling the unconventional isotope effect of BiS2-based superconductors in ambient-pressure structure,the switch of superconductive mechanism may ascribe to structural symmetry breaking induced by high-pressure effect.This is an important step toward the clarification of the origin of superconductivity for BiS2-based system in high-pressure phase.In the future, thorough research on BiS2-based superconductors for both ambient- and high-pressure phases is very essential and necessary.

Fig.4.Variation of Tc difference Δln(Tc)between32S and34S samples,and isotope coefficient α with pressure in a range of 12 GPa-18 GPa.
4.Conclusions
Using the first-principles calculations, we reported the substitution effect of32S by the heavier isotope34S on the phonon spectra, electron-phonon coupling factor, and the superconductivity of LaO0.5F0.5BiS2in high-pressure monoclinic phase.The electron-phonon coupling factor can reach to 0.61, and corresponding isotope coefficient is estimated to be 0.13≤α ≤0.20.It should be noted that the calculatedTcof high-pressure phase is lower than the experimental result.Therefore,we confirm the vital role of moderate phononmediated pairing in determining the superconductivity of highpressure phase.However,to further clarify the nature of superconductivity in BiS2-based superconductors,cooperative multiple paring interactions still need studying in future.
Acknowledgements
Project supported by the National Natural Science Foundation of China(Grant No.12175107)and the Natural Science Foundation of Nanjing University of Posts and Telecommunications(Grant Nos.NY219087 and NY220038).
- Chinese Physics B的其它文章
- Corrigendum to“Reactive oxygen species in plasma against E.coli cells survival rate”
- Dynamic decision and its complex dynamics analysis of low-carbon supply chain considering risk-aversion under carbon tax policy
- Fully relativistic many-body perturbation energies,transition properties,and lifetimes of lithium-like iron Fe XXIV
- Measurement of the relative neutron sensitivity curve of a LaBr3(Ce)scintillator based on the CSNS Back-n white neutron source
- Kinesin-microtubule interaction reveals the mechanism of kinesin-1 for discriminating the binding site on microtubule
- Multilevel optoelectronic hybrid memory based on N-doped Ge2Sb2Te5 film with low resistance drift and ultrafast speed

