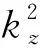柱坐标系下亥姆霍兹方程解的分类及典型应用
马子寅,陈文琼,梅中磊
(兰州大学 信息科学与工程学院 光电子与电磁信息研究所,甘肃 兰州 730000)
亥姆霍兹方程是用于表述电磁波传播规律的椭圆偏微分方程,在分析理想各向同性介质的边值问题时,通过对麦克斯韦方程组进行变换,可以得到介质中的电场、磁场以及它们的各个分量均满足亥姆霍兹方程[1].对亥姆霍兹方程进行求解可以定量地计算出场分布的解析解.对应不同的坐标系,亥姆霍兹方程具有不同的显示形式,根据待求解问题边界条件的不同,应当选择适合的正交坐标系,对方程进行分析求解.柱坐标系是常用的正交坐标系之一,在柱坐标系下对亥姆霍兹方程求解可计算出圆波导、圆谐振腔、同轴线等结构的场分布[2].目前,许多教材中对圆柱坐标系下的分离变量法进行了介绍[3,4],但并没有从根本上分析亥姆霍兹方程通解形式与电磁学问题之间的深层关联.本文从柱坐标系下亥姆霍兹方程分离变量法求解出发,分析了通解的不同形式与电磁波状态的对应关系,并通过数值计算和电磁仿真的方式验证了不同形式的通解对应的典型电磁问题.本文的内容对“电磁场与电磁波”“微波技术”等课程的教学及科研具有一定的指导意义.
1 亥姆霍兹方程在柱坐标系下的分离变量法
1.1 柱坐标系下的亥姆霍兹方程的导出
在直角坐标系下,亥姆霍兹方程可表示为
(1)
已知直角坐标系与圆柱坐标系间变量代换关系:
(2)
对式(2)分别求x和y的一阶偏导可得
(3)
根据链式求导方程可知
(4)
对式(4)再次求导可得
(5)
(6)
将式(5)、(6)代入到式(1),得到柱坐标系下的亥姆霍兹方程:
(7)
式(7)即为柱坐标系的亥姆霍兹方程,k为波数:
(8)
根据其物理意义可知,在无耗介质中,k的值恒大于0.
采用上述推证方式,形式上看似复杂,但其避免了一般情况下的正交曲线坐标系的问题,更加有利于初学者的理解.
1.2 分离变量法求解
分离变量法的作用是将一个偏微分方程分解为多个只含有一个变量的常微分方程,它是求解亥姆霍兹方程边值问题的一种常用方法.
根据上一小节得到的柱坐标系下的亥姆霍兹方程,设待求解函数为
u(r,φ,z)=R(r)Φ(φ)Z(z)
(9)
将式(9)代入到式(7)中并化简可得
(10)
移项可得下式
(11)
等式左边为关于变量r和z的函数,等式右边为关于φ的函数.若要等式成立,则等式两边必须等于一个常数,设这个常数为n2.则可得到
Φ″+n2Φ=0
(12)
由于已知关于φ的函数必须满足周期性边界条件,即
Φ(φ)=Φ(φ+2π)
(13)
因此,关于φ的函数的通解为
Φ(φ)=Acosnφ+Bsinnφ, (n=0,1,2,3,…)
(14)
当n=0时,式(14)为常数,对应于电磁问题中的轴对称形式.
将式(11)等式左侧部分再次应用分离变量法:
(15)
(16)
(17)
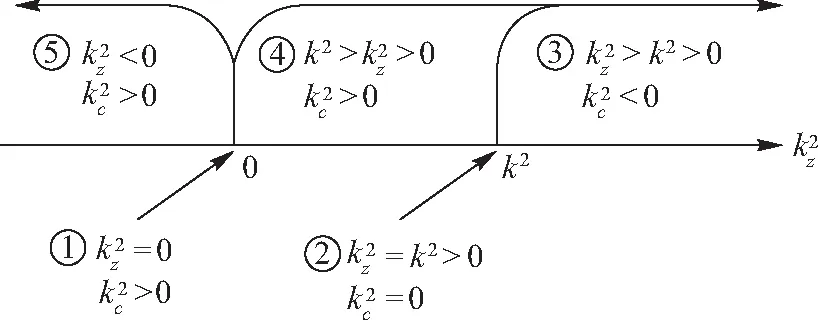
图1 柱坐标系下亥姆霍兹方程分离变量的5种取值情况
1.3 解的形式的讨论
当kz2>0时,方程(16)的通解为三角函数的线性组合或复指数函数的线性组合:
(18)
一般情况下,数学上不同表达形式对应的解是等价的.但对于电磁场问题,则需要分析解的形式是否适用于当前问题的求解.上式中三角函数表示的是z方向的驻波,而复指数形式表示的是行波.
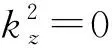
Z(z)=C+Dz
(19)
当系数D=0时,函数与z无关.对应于电磁问题中的二维场情形.
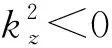
Z(z)=C′eδz+D′e-δz=Cshδz+Dchδz
(20)
一般情况下,当z方向为有界时,选择双曲函数更方便计算;反之,当z方向无界时,一般选择指数衰减的函数形式.
(21)
与z方向函数类似,当径向传播的波为行波时,径向函数的解应为第一类和第二类汉克尔函数的线性组合,且分别对应了沿径向发散的波和汇聚的波;而当径向传播的波为驻波时,则径向函数的解为贝塞尔函数和诺伊曼函数的线性组合.值得注意的是,由于诺伊曼函数在r→0时,函数值趋近于无穷,因此,若求解区域包含柱轴,则解不应包含诺伊曼函数.
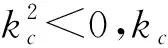
R(r)=EIn(γr)+FKn(γr)
(22)
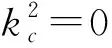
(23)
根据上述讨论,并结合图1中的5种情况,很容易得到相应条件下亥姆霍兹方程的通解形式.下面结合数值计算和电磁仿真的方法,给出这5种不同的通解形式所对应的典型的电磁应用情景,便于初学者学习和理解.
2 在电磁学中的应用案例
现结合图1中的5种情况以及1.3节中的解的具体形式,对各种解所对应的物理场景进行介绍.
2.1 当且时的典型应用
情况1的典型应用就是圆柱型谐振腔.当前情况下场沿z向均匀分布,即谐振腔内部的场强不随z的取值而发生变化.对于TM模式,有
u(r,φ)=Ez=Jn(kcr)(B1ncosnφ+B2nsinnφ)
(24)
图2给出了TM010模式的电场分布,可以看出,该电场的分布不随z变化;由于n=0,场满足轴对称的性质.
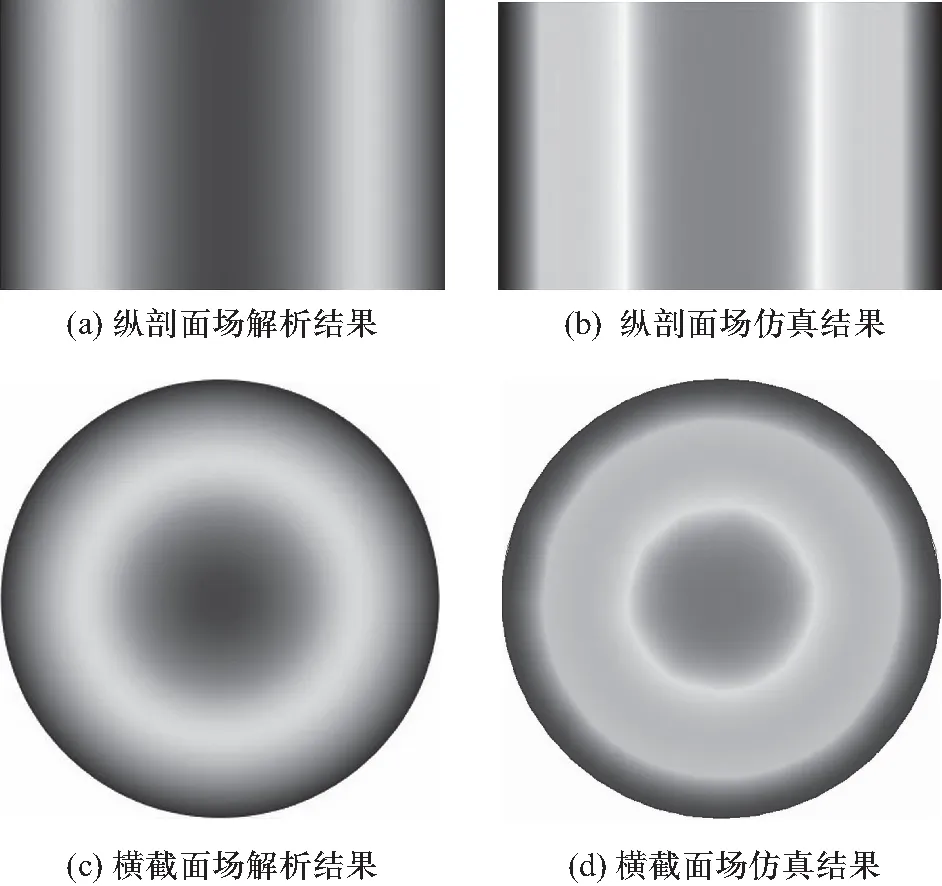
图2 TM010模圆谐振腔电场分布
图3给出了TM110模式的电场分布,电场的分布不随z变化.但由于n≠0,所以场不满足轴对称的性质.

图3 TM110模圆谐振腔电场分布

图4 TEM模同轴线横截面电场分布
2.2 当且时的典型应用
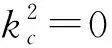
u(r,φ,z)=Er=(Ern+Fr-n)(B1ncosnφ+B2nsinnφ)e-ikzz
(25)
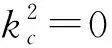
u(r,φ,z)=Er=(Ern+Fr-n)·
(B1ncosnφ+B2nsinnφ)(C1coskzz+C2sinkzz)
(26)
同轴谐振腔的剖面场分布如图5所示.

图5 TEM模同轴线谐振腔纵剖面电场分布
2.3 当且时的典型应用
情形3经常用于描述边界表面处的倏逝波,比如光纤中包层内的场分布.光纤是由纤芯和包层组成的同心柱状玻璃体,光纤纤芯折射率高于包层中的折射率,以特定角度传输的光波在光纤纤芯及包层之间发生全反射,实现光波低损耗传播[5,6].传播常数β=kz是描述光纤传输特性的重要参数,光纤中传输模式的传播常数被限制在一定范围内,即
k0n2 (27) 其中,n1为纤芯的折射率,n2为包层的折射率.阶跃折射率光纤的纵向分量满足亥姆霍兹方程,对应的径向函数满足 (28) 根据传播常数β的取值范围可知,当i=2时,即对包层的纵向分量进行求解时,径向函数满足虚宗量贝塞尔方程,径向函数的解为虚宗量贝塞尔函数和虚宗量汉克尔函数的线性叠加.由于求解的区域包含r→∞,因此通解不应包括虚宗量贝塞尔函数.包层中的场函数(纵向电场或者磁场)为 (B1ncosnφ+B2nsinnφ)e-ikzz (29) n=0时,可绘制光纤横截面上的场强分布如图6所示,其中黑色圆圈之外的区域表示的就是包层.可以看出,远离分界面的地方,场强逐渐减小,从而使得光场主要被束缚在纤芯内部. 图6 光纤包层横截面电场分布 圆波导是指截面为圆形的空心金属波导管,是微波系统中的基本传输线之一.圆波导中沿轴向传播电磁波,因此关于z的函数应为行波形式,且只需要考虑沿一个方向传播.对于圆波导问题,显然求解区域包含柱轴,因此解不包含诺伊曼函数.根据上述分析和线性叠加原理可以列出圆波导中TE模式的场函数: u(r,φ,z)=Hz=Jn(kcr)(B1ncosnφ+B2nsinnφ)e-ikzz (30) 利用式(30)绘制TE21模场强分布如图7(a)所示. 如果将圆形波导的两端用金属封闭起来,就可以得到圆柱形谐振腔,一般情况下,其在轴向形成驻波,因而有 u(r,φ,z)=Hz=Jn(kcr)(B1ncosnφ+B2nsinnφ)· (C1coskzz+C2sinkzz) (31) 情况5描述的也是分界面上的倏逝波,当分界面处的表面阻抗为感抗或者容抗形式时,可以分别支持TM或者TE形式的表面波[7].近年来,对于二维电磁超表面的研究如火如荼,利用其中的阻抗超表面,就可以激励和支持这种类型的表面波,且在全息天线的设计中得到了广泛的应用[8,9].这类倏逝波可分为倏逝驻波和倏逝行波,两者之间的区别在于径向波的形式为驻波还是行波.比如,TM模式的电场函数可分别表示为 u(r,φ,z)=Ez=Jn(kcr)(B1ncosnφ+B2nsinnφ)e-δz (32) (33) 在一个底部覆盖介质的圆柱谐振腔中,可以激励和支持这种形式的倏逝驻波.其电场分布如图8所示.其中,图8(e)给出了纵截面上的磁场分布矢量图,从中可以看出,远离介质和空气表面的地方,场逐渐衰减,因此是一种非常典型的表面波.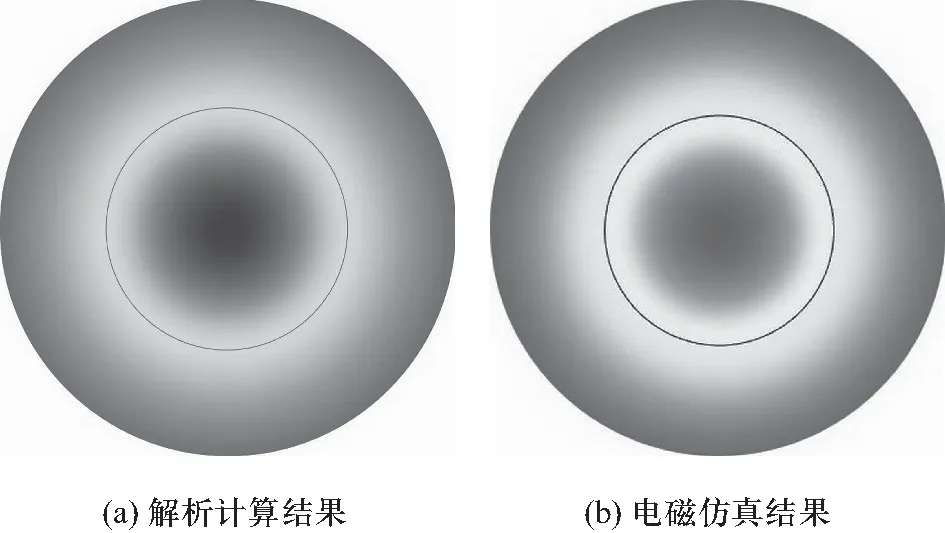
2.4 当且时的典型应用
2.5 当且时的典型应用
3 结语