加工中心体积热误差在线建模与实时补偿

姜 辉, 朱炜炜

(1.上海交通职业技术学院 轨道交通学院,上海 201101,E-mail: jianghuiscp@126.com;2.宁波科威联创数控技术有限公司,浙江 宁波 315400)

随着高效、高速精密加工中心不断发展,热变形成为影响其精度的主要因素,热误差控制是当前领域研究热点。目前研究包括热平衡设计[1]、冷却装置设计[2-4]、热变形约束、热优化设计[5-7]、热误差补偿[8]等方面。通过热对称结构设计减小热变形方法已在数控机床上广泛应用,对减小径向热变形具有重要意义;但是,热对称结构无法减小各个方向热变形,特别是轴向热变形、热翘曲、热倾斜等热变形,而数控机床主轴轴向热变形是影响加工精度的主要因素之一。冷却装置的应用大幅减小数控机床热变形,常用冷却方式包括水冷[9]、空气强制对流冷却、热管冷却[10]、油雾冷却等;但是,需要探索对主轴等关键热源深度冷却技术。通过将热变形转移到不影响机床精度方向或采用热变形系数小的材料来实现热变形约束方法,可以减小数控机床某个方向热变形,例如基于碳纤维热缩特性的热变形约束创新热设计理论[11],可大幅减小主轴箱热变形;但是,热变形约束法无法约束电主轴各个方向热变形,特别是芯轴热变形。

误差补偿法是通过建立热变形与关键测温点温度数学模型,应用外部坐标偏移、修改G代码等技术实现热误差实时补偿[12-13],该方法优点是不改变数控机床结构,但补偿精度受误差模型精度及鲁棒性影响。随着建模方法及计算机技术不断发展,机床误差建模精度大幅提高[14-16],对提高误差补偿精度具有重要意义。但是,现有建模方法具有复杂性和依赖建模软件等缺陷,难以实现数控机床体积热误差在线建模。

为实现体积热误差在线建模,提出基于正交多项式做最小二乘建模法,设计开发基于LabView的在线建模系统,大幅提高加工中心体积热误差建模精度及效率。为实现体积热误差在线实时补偿,研发基于轴偏置误差补偿功能的在线补偿系统,大幅提高加工精度。

1 体积热误差在线建模机理

1.1 体积热误差建模机理

由不同温度下体积热误差曲线形状与初始几何误差曲线形状一致,只是绕某一点旋转一角度,即不同温升状态下的热误差曲线形状相似但斜率随温度变化。热误差曲线形状取决于机床几何误差,热误差曲线斜率则反映机床运动产生热变形对几何误差的放大效果,其数值取决于机床部件温升。因此,可将体积热误差分解成两个部分:几何误差以及与斜率相关的热误差,即:

(1)

对于几何误差δuv可用多元回归法、最小二乘法、正交多项式法、遗传算法、傅立叶级数法、牛顿插值法等进行建模,其基本思路都是建立目标函数并寻找其极值,建模精度与所选函数阶次有关。对于热致误差斜率可采用MatLab、最小二乘法等进行求解。将各误差元素建模结果代入综合误差模型可得加工中心体积热误差数学模型。为实现体积热误差在线建模,设计开发基于正交多项式做最小二乘的在线建模系统。

1.2 体积热误差在线建模系统设计

体积热误差在线建模系统通过LabView开发,该系统自动读取数据库热误差及温度数据,后台自动生成几何误差及与斜率相关的热误差模型,并将拟合曲线输出至如图1所示显示屏;然后将各误差元素模型输出至体积热误差综合数学模型,完成体积热误差模型建立。在线建模系统通过上位机与补偿系统串口通讯,自动将最新体积热误差模型加载到误差补偿系统的数据存储模块,创建体积热误差模型或对原有模型更新。为在线补偿系统提供体积热误差计算模型。上位机在线建模系统自动记录并显示体积热误差补偿前后数据,自动识别激光干涉仪、球杆仪等测量设备的数据格式;直观显示补偿前后体积热误差变化情况(如图2所示),为体积热误差实时补偿效果评估提供依据。在线建模系统的建模原理如下。

图1 上位机在线建模界面

图2 上位机数据分析界面

由于机床冷态几何误差与机床坐标位置呈比例关系,为实现自动建模,采用正交多项式做最小二乘法建立机床冷态几何误差:

δu(v)=a0φ0(v)+a1φ1(v)+a2φ2(v)+…+anφn(v)

(2)

式中:δu(v)为几何误差;u、v表示坐标轴X、Y、Z;a0,a1,…,an为回归系数;φ0(v),φ1(v),…,φn(v)为正交多项式,可由

式(3)计算。

(3)

式(2)-式(3)中各系数可由式(4)-式(6)计算。

(4)

(5)

(6)

应用式(2)-式(6)可建立几何误差数学模型。图3为基于正交多项式做最小二乘自动建模流程。

图3 几何误差线建模流程

第一步,根据实测几何误差应用式(6)求解a0;

第二步,将φ0(x)代入式(4)计算系数ξ1,将ξ1、φ0(x)代入式(3)计算正交多项式φ1(x),将φ1(x)、φ0(x)代入式(6)计算系数a1;

第三步,将φ1(x)代入式(4)计算系数ξ2,将φ0(x)、φ1(x)代入式(5)计算系数β1,将ξ2、φ1(x)、β1、φ0(x)代入式(3)计算正交多项式φ2(x):应用式(6)计算系数a2;

第四步,重复第三步,直至系数ak超出设定值10-9计算结束,将各步计算结果代入式(2)可得几何误差模型。式(7)为几何误差在线建模结果,建模数据为基于温升可重复的分步体对角线法测得某加工中心体积热误差,所建立数学模型适合单片机处理,方便误差补偿系统数据处理。

(7)

与斜率相关热误差数学模型通过最小二乘法编程建模,分别在X、Y、Z轴及主轴选取两个关键测温点作为热误差建模温度数据,根据某加工中心热误差检测数据,应用最小二乘法线性拟合,得到各误差曲线的斜率,代入式(1)可得热误差模型如式(8)。

(8)

将式(7)-式(8)代入体积热误差综合数学模型,可得该加工中心体积热误差模型如式(9)-式(11)。

Δx=-14.102-0.003 86x+0.000 173x2-3.8×10-7x3+
2.56×10-10x4+0.01y-0.000 37y2+1.3×10-6y3-
1.1×10-9y4-0.06z-1.16×10-4z2+7×10-7z3-
10-9z4-x×(-0.163 8+0.001 7×Tx1+0.004 6×Tx2)-
2.66×TS1+3.188 2×TS2

(9)

Δy=30.74+7.73×10-9x3-5.18×10-5x2+0.041x-
0.023 4y+0.000 275y2-3.143 3×10-7y3-
0.015z+2×10-5z2-1.006 3×TS1-0.246 2×TS2-
y×(-0.169+0.001 4×Ty1+0.005 1×Ty2)+
z×(-0.093 6+0.002 1×Tz1+0.001 5×Tz2)

(10)

Δz=42.3+0.001x-3.1×10-6x2-0.04y-0.000 3y2+
1.12×10-6y3-1.4×10-9y4-
0.020 5z+0.000 026 9z2-1.76×10-7z3-
x×(-0.083 2+0.001 4×Tx1+0.001 8×Tx2)+
z×(-0.166 4+0.002 1×Tz1+0.004 3×Tz2)-
y×(-0.074 6+0.002×Ty1+0.001 1×Ty2)+
2.325×TS1-4.131 2×TS2

(11)

由体积热误差综合模型,可分析该加工中心体积热误差的空间分布。图4为X向体积热误差在YOZ平面分布,由图4可以看出,加工中心X向体积热误差与机床X、Y、Z轴位置有关,同时又与机床温度有关,随着机床温度升高,在x=400 mm处的X向热误差沿负向增大,运行2 h后X向热误差沿负向增加5 μm,这主要是由主轴沿X向热漂移引起。

图4 不同方法诊断结果的标准差

图4 X向体积热误差空间分布

图5为Z向体积热误差空间分布,图5(a)为机床运行2 h后Y=100 mm、500 mm处Z向热误差在XOZ平面内分布,不同Y坐标下Z向体积热误差形状基本保持一致,并且随着Y轴正向移动Z向误差逐渐减小,说明Y轴导轨是倾斜的。图5(b)为机床运行2 h后在Z=0 mm处Z向体积热误差在XOY平面内分布,Z向热误差最大为-75 μm,这主要是由于主轴箱及主轴膨胀引起。

图5 Z向热误差空间分布

由图4、图5可以看出,加工中心体积热误差具有复杂非线性特点,应用在线建模软件可实现体积热误差精确建模,且建立模型适合单片机处理,为体积热误差在线实时补偿提供依据。

2 体积热误差在线补偿机理

2.1 误差补偿原理

现代很多数控系统中均有开放的轴偏置误差补偿功能(Axis Offset Error Compensation, AOEC),AOEC功能可在机床加工过程中改变机床坐标系与参考基准之间的相对位置,从而使各坐标轴发生偏置,这种坐标轴偏置可实时调整刀具与工件之间相对位置以达到误差补偿目的,其补偿原理如图6所示X轴偏置过程。

图6 轴偏置误差补偿原理

假设在机床加工过程中,刀具理想轨迹沿X方向从点A运动到点B,由于机床存在各项误差,刀具运动到B′,从而在X方向上刀具理论位置与实际位置之间存在误差Δx。此时可通过AOEC功能,使机床坐标系X轴零点相对于参考基准偏置Δx,形成新机床坐标系。由于数控系统中记录的刀具在机床坐标系中的坐标值没有发生改变,所以机床X轴会自动使刀具在X方向同步偏置Δx以保持其在新机床坐标系中的坐标值。当然由于机床运动误差,偏置运动完成后,刀具实际位置也不一定完全到达理想位置B,假设最终刀具位置为B″。可以肯定的是B″要比B′更接近理论位置B,经过上述轴偏置过程,可以达到误差补偿效果。需要强调的是,上述轴偏置过程的结果是坐标轴与刀具相对于参考基准整体发生偏置,刀具在机床坐标系中的坐标位置并不会发生改变,所以这种基于轴偏置的补偿过程不会对数控系统执行的数控程序产生影响。

AOEC补偿功能不需要额外触发指令,机床PLC会自动循环扫描对应的数据地址,只要在对应地址设置补偿量数据,系统就会立即响应完成补偿动作。基于数控系统AOEC功能,如果将机床各运动轴实时体积热误差数值发送至PLC对应地址,可实现对机床体积热误差同步实时补偿。为实现误差在线同步补偿,研发基于P89V51RD2单片机的数控机床误差在线补偿系统。

2.2 在线补偿机理

为实现体积热误差在线补偿,研发基于单片机P89V51RD2的误差补偿系统,在线补偿流程的一个完整补偿循环包括如图7所示5步:

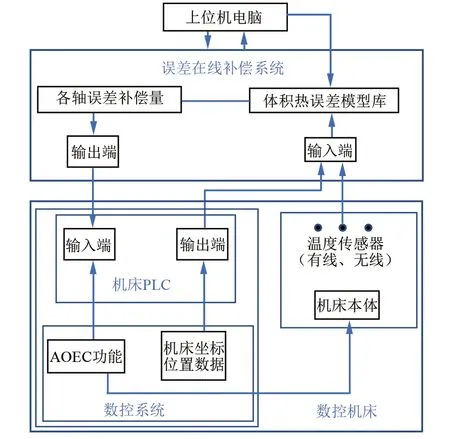
图7 体积热误差在线补偿流程

(1) 在线补偿系统实时读取温度传感器温度数据,经过滤波与后处理,将温度数据发送至体积热误差模型(式9～式11)。

(2) 从PLC输出端读取机床各运动轴实时位置坐标,发送至体积热误差模型(式9～式11)。

(3) 体积热误差在线补偿系统根据读取温度数据以及机床各运动轴实时位置坐标通过误差模型实时计算误差值。

(4) 误差补偿量经误差补偿系统输出接口卡发送至PLC输入端。

(5) PLC输入端实时扫描补偿量数据,在数控系统内部传输至AOEC功能指定的轴偏置量存储地址,并对各轴偏置量做出响应,完成误差补偿的一个循环。

在进行体积热误差在线补偿前需要完成如下工作:首先在数控系统中编制PLC程序,将系统指定的轴偏置量存放地址与PLC输入端的设定地址、以及机床坐标数据存放位置与PLC输出端的设定地址进行匹配,编制对应WMOVE(PLC数据移动)函数语句;并将误差在线补偿系统的输入端与设定的机床PLC输出端地址连接,误差在线补偿系统的输出端与设定的机床PLC输入端地址连接。其次在机床各关键测温点布置温度传感器,通过有线或无线方式与误差在线补偿系统连接。最后连接上位机与误差在线补偿系统,向补偿系统中单片机烧录运行程序,向补偿系统数据存储地址传输体积热误差模型。

3 在线补偿实验

为验证体积热误差在线补偿效果,将误差补偿系统与某加工中心数控系统连接如图8所示,机床X、Y、Z轴行程分别为800 mm、500 mm、500 mm,主轴最高转速为18 000 r/min。将1.2节建立的体积热误差模型(式9～式11)输入到误差补偿系统相应存储地址,系统调试后进行体积热误差补偿实验。

图8 体积热误差在线补偿实验

机床空运行,X、Y、Z轴运行速度为f=2 m/min,机床工作台在全行程内匀速运行,运行1 h后应用激光干涉仪检测机床X、Y、Z轴定位误差,图9为X、Y、Z轴定位误差补偿前后结果。表1为加工中心补偿前后体积热误差对比。由表1可以看出,补偿前该加工中心X、Y、Z最大体积热误差分别为8.965 μm、45.011 μm、19.241 μm;经误差实时补偿系统补偿后,X、Y、Z最大体积热误差分别为1.901 μm、4.716 μm、3.263 μm;机床精度大幅提高,最大可提高89.5%,这一补偿结果使数控机床的精度等级提高一个数量级,对提高数控机床精度及加工精度具有重要意义。

表1 体积热误差补偿前后对比

图9 补偿前后体积热误差

4 结论

体积热误差是影响数控机床加工精度的主要因素之一,具有复杂非线性特点。应用正交多项式做最小二乘方法建模使建模效率大幅提高,模型适合单片机处理,能有效避免其它建模方法的病态问题及由于预估误差模型而引入的预估误差及手工建模引入的舍入误差,大幅提高体积热误差建模精度,为高速加工中心体积热误差在线实时补偿奠定基础。

基于轴偏置误差补偿功能可实现体积热误差在线实时补偿,实验结果表明,经体积热误差补偿后,加工中心精度最大提高89.5%。证明误差补偿技术是提高数控机床精度及加工精度经济有效的方法,可在不提高机床本身精度前提下,获得比机床精度更高的加工精度,为实现国产数控机床由微米级向微纳级发展奠定基础。