GPS精密水准网数据处理优化策略

林振通

(深圳市水务规划设计院股份有限公司,广东 深圳 518109)

0 引 言

以GPS(全球定位系统)为核心的卫星导航定位技术应用在中国已经有近20a的发展历程,正向更高层次、更广阔领域发展[1]。目前,GPS在监测地壳形变方面具有重要作用,这些形变是由自然力量和人类活动的影响所引起的[2]。有研究人员开展了利用GPS确定地表变形参数的研究,孙英翔等基于GPS静态测量与水准测量相结合的方法获得了一定周期内的矿山地表沉降位移数据[3]。段成宝等对某煤炭基地采空区地表变形进行GPS数据分析,实现对地表变形量进行有效预测[4]。一些研究结果表明,可以用精确的GPS(全球定位系统)/GNSS(全球导航卫星系统)测量取代经典的水准测量。然而,这需要最先进的设备和数据处理软件和算法,且需要消除或大幅减少系统误差。因此,必须应用先进的信号传播模型来减少电离层和对流层延迟,还需要消除硬件偏差[5-6]。

文章对卫星精密水准中GPS数据的优化处理策略进行了研究,所有数值试验均采用BERNESE 5.0软件进行处理。研究的重点是优化参数选择,包括观测时长、控制网几何形状、电离层延迟等。

1 测试数据

为了进行分析,选择了一个20km×60km的矿区作为试验区,假设网络节点之间的距离在510 km范围内。

在2条经典水准线上同时进行了经典几何水准和卫星水准测量,其中包括19个监测点(记作PP和LL)和5个控制点(第一类基准,记作RR)。2个监测点(LL01和LL02)用于连接2条水平线。使用了GBAS地基增强系统的几个参考站的全球定位系统数据,控制点的正常高度范围为88.596～178.560m,监测点的正常高度范围为90.725～175.918m。中间基准允许在GPS天线强制定心的情况下实现卫星测量。

在第1条水准线上,进行了2次8 h的同步观测,每个点总共要测量16 h。在第2条水准线上,进行了1次8 h的同步观测。控制点(RR)观测5个阶段,每次8 h。卫星测量在以下假设条件下进行:GPS接收机:16套,控制点观测时间:8 h;监测点的观测时间:8 h;控制点观测次数:5次;监测点观测次数:1次或2次;GPS频率:L1和L2;GPS测量值:伪距和载波相位;观测间隔:5 s;截止高度角:0°;点位几何图形强度因子PDOP最大值:6;用专用装置将卫星天线强制定心在水准基准上。

2 数值试验和处理策略

本研究使用BERNESE 5.0软件处理数据。由于垂直地面变形监测中最重要的参数是监测点的高度坐标,因此了解天线参考点的平均相位中心偏移(PCO)和相位中心变化(PCV)至关重要。此外,天线相位中心的主要误差源是垂直偏移。用于大地测量的GPS天线在形状、结构和制造它们的材料方面有很大的不同。因此,需要应用精确的天线PCO和PCV校准。在本研究中,使用了IGS(国际GNSS服务)导出的绝对天线PCV校准,还应用了GPS卫星天线的IGS PCV模型、IGS最终卫星轨道和时钟、地球自转参数以及行星星历表。

2.1 控制点

在ITRF2008参考系中确定运动周期平均tc=2012.55时的5个控制点坐标。选择了4个EPN参考站——WROC、CLIB、BOR1和GWWL,将测试网络连接到ITRF2008。此外,国家全球定位系统网络的3个常设站(GLOG、LEGN和ZARY)也包括在内,使用ASG-EUPOS站作为额外的高质量控制点。

在5个8 h长的时段中对对照点(RR和ASG-EUPOS)进行了观测,使用以下假定条件进行计算:电离层模型:无电离层线性组合(L3);模糊度分辨率:SIGMA L5和L3;对流层:湿延迟NFM映射模型;高度截止角:10°。

表1给出了获得的控制点高度坐标的平均重复性。根据所有观测获得的高度的最终调整,将每个点的重复性计算为均方根(RMS)。可以注意到,ASG-EUPOS站获得了更好的重复性,该站的平均高度分量重复性分别为2.9 mm和4.6 mm,RR点的平均高度分量重复性为4.6 mm,所有控制点的平均重复性为4.0mm。

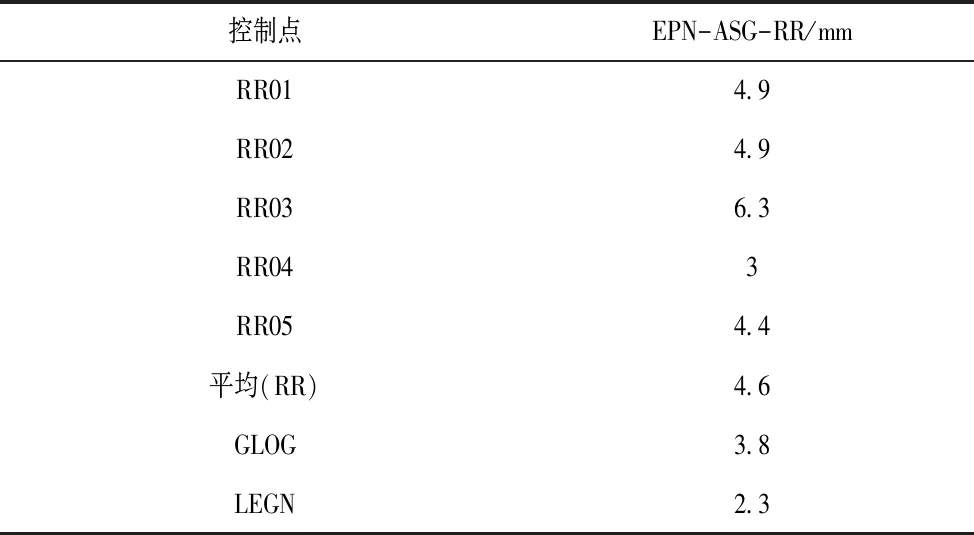
表1 控制点的平均高度重复性(基于5次8h的处理)

2.2 监测点

为了分析处理在监测点收集的GPS数据得到的高度分量的可实现精度,测试了几种处理策略和假设。参数如下:控制网几何形状:“星形”或多边形;观测时长:8 h、4 h、2 h;电离层模型:CODE全局模型或无电离层模型;频率:带有电离层模型(L1)或无电离层线性组合(L3);对流层:干延迟NFM映射模型;卫星截止高度角:5°、10°、15°。

综上,超过80种策略被测试。然而,文章只介绍了18个选定测试的结果,以下所有的研究策略均参照:观测时长:4h;电离层模型:CODE全球电离层模型(L1);对流层建模:湿延迟NFM映射模型;卫星截止高度角:5°。

2.2.1 控制网几何形状

由于测试网络的跨度很大,而且它有两个目的,一是测量突发大地构造事件区域内选定的几个监测点;二是定期监测整个网络以进行变形分析。因此我们提出了两种几何形状的控制网:(1)“几何1”:将每个监测点分别连接到3个控制点,监测点之间没有任何基线,这是调查突发事件影响的情况。(2)“几何2”:反映了有规律的水平线与连接相邻监测点的基线,这是对整个网进行定期监测的情况。

一方面,“几何1”中的每一个监测点都可以单独测量,并与参考点直接相连。这样,一个点的测量误差就不会传播到另一个点。另一方面,“几何2”中处理的基线较短,这可以更好地减少相关误差。所有的数值测试都是针对这两种情况进行的,得到的结果不同,这是由于2种情况下的基线长度存在很大差异。

表2展示了获得的监测点的高度分量的可重复性,这些高度分量是基于2个或4个4h的观测结果得出的。可以注意到,“几何1”的平均可重复性是3.2 mm,而“几何2”的平均可重复性略微增加到3.3 mm。

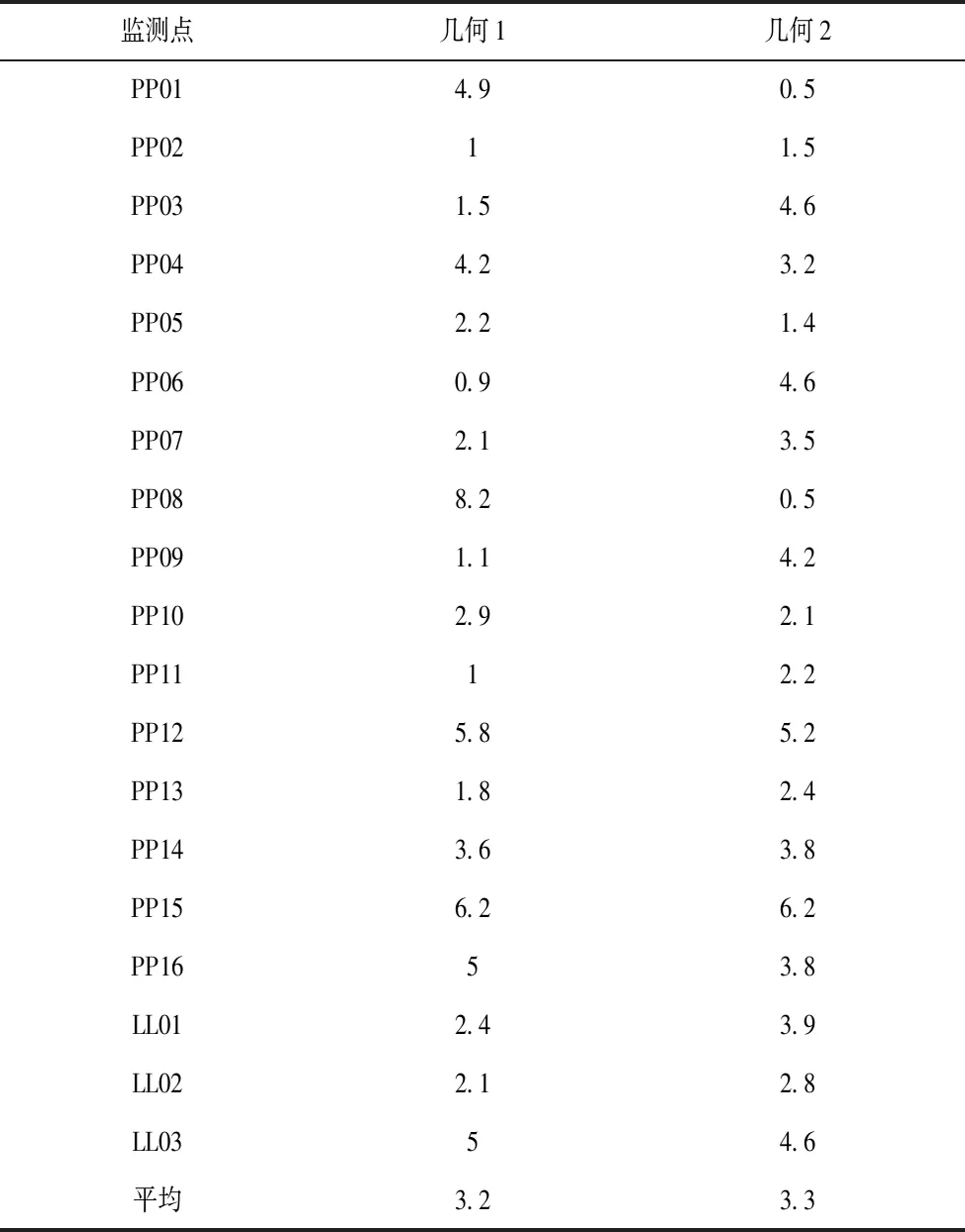
表2 椭球高度分量的可重复性与参考策略和两个网络几何形状 mm

结果表明,当使用“参考”策略处理两种情况时,会得到相似的结果,并且也证实了“几何1”不会降低精度,可以用于整个控制网的定期监测情况。其主要优点之一是影响一个监测点的测量误差不会传播到相邻点。

2.2.2 观测时长

观测时间的长短会影响测量的成本,因为在1天中可以进行1次8 h的测量,2次4 h的测量或4次2 h的测量。假设缩短观测时间可以使我们同时测量更多的监测点,显然降低成本的同时,也会导致结果准确性的降低。

文章在2 h、4 h和8 h使用“参考”策略,其他参数保持不变。值得注意的是,PP01-PP08点是在8 h的观测结果中调查的,因此,在处理8 h观测时长的情况下,不可能保证它们的重复性。不同观测时长处理得到的监测点椭球高的重复性如表3所示。

表3 不同时段得到的椭球高度分量的重复性 mm

表3给出的结果证实了一个假设,即较短的观测时间导致较不准确的结果。“几何1”中从8 h获得的高度分量的平均重复性达到2.8 mm,而2 h的平均重复性超过4.5 mm。结果显示,在8 h和4 h中,“几何1”比“几何2”更有优势。然而,2 h时“几何2”提供了更好的结果。这是由于在“几何1”处理更长的基线需要更长的观测时间。结果表明,使用GPS调平,可以得到优于3 mm的精确椭球高度,建议将观测时间设为4 h是测量成本和结果准确性之间的最佳选择。

2.2.3 电离层模型

电离层延迟对GNSS观测有明显的影响,由于精确定位主要是在相对模式下进行的,因此大大降低了10～20 km以上基线上电离层延迟的影响。“几何2”的情况下,其最长基线为10 km。然而,在“几何1”下处理的基线长度通常超过40 km(最大46 km)。

有电离或无电离层模型获得的椭球高度分量的重复性结果见表4,发现“几何1”中电离层模型的应用提高了结果的准确性。高度分量的重复性从3.6 mm提高到3.2 mm,这可以用处理较长的基线(46 km)来解释。与在“几何2”的较短基线(10 km)相比,这些基线受电离层延迟剩残差的影响较大。因此,在后者中并无改善。

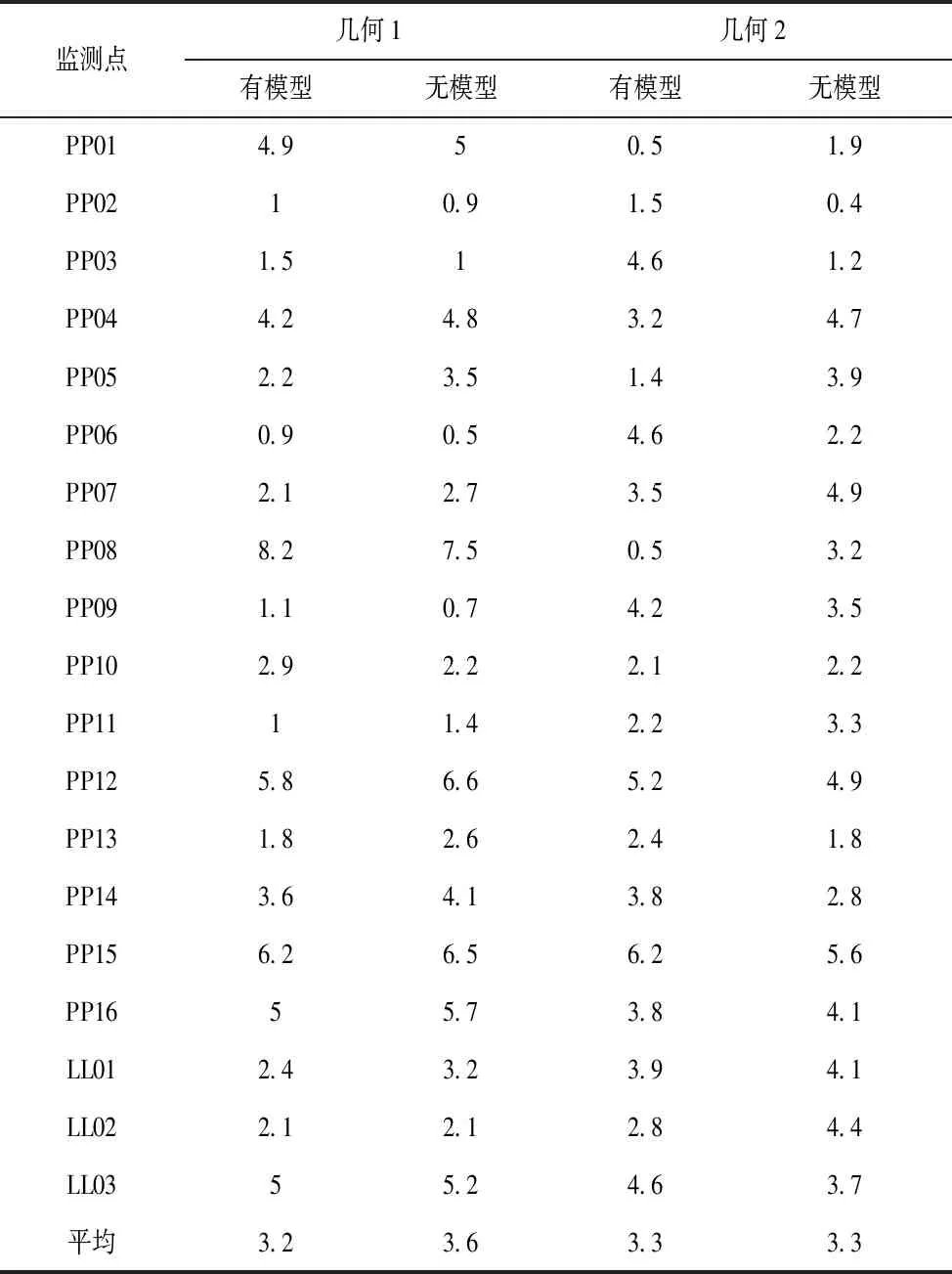
表4 有电离或无电离层模型获得的椭球高度分量的重复性 mm

根据表4给出的结果,建议应用电离层模型,特别是在“几何1”的情况下。注意到应用CODE电离层模型时,如果出现区域性电离层扰动,该模型可能不够。因此,建议尽可能使用区域或本地的模型。

3 结 论

本研究分析了基线在50 km以下的精密卫星水准网的处理问题。根据上述数值试验,提出了以下结论和建议:①处理后的控制网的几何形状对结果影响不大;②无论网络几何形状如何,可采用通用的数据处理策略;③4h的观测时间允许高度分量的重复性约为3mm;④建议使用具有电离层模型的单频数据来降低电离层延迟残差。

所得结果的精度证实,卫星测量可以有效地取代经典的几何精密水准测量,特别是在不需要正交测量或标准高度系统的高度应用中(地面变形研究)。