主被动光学卫星遥感数据融合浅海水深测量

张春玲,李由之,张 刚,邱振戈

(1. 河南省地图院,河南 郑州 450008; 2. 南京大学地理与海洋科学学院,江苏 南京 210023;3. 北京四维远见信息技术有限公司,北京 100070; 4. 中国测绘科学研究院,北京 100830;5. 上海海洋大学海洋科学学院,上海 201306)

浅海水深数据是浅海环境治理、浅海资源开发利用、浅海航行、登岛作战等经济军事应用所需要的重要基础地理空间信息,准确、高效、经济地获取浅海水深数据是海洋测绘目标[1]。与传统声学手段的水深测量相比,光学卫星遥感技术具有低成本、可重复观测、不受通航条件限制的优势,已成为浅海水深测量的重要手段。双介质立体摄影测量和激光雷达测深是现阶段主要的两种光学卫星遥感测深手段。其中,双介质立体摄影测量属于被动光学遥感测量技术,能够快速、高效、大范围地获取遥感影像覆盖区域的水深信息,但水深反演精度相对较低[2];而激光雷达测深技术属于典型的主动光学遥感手段,虽然水深测量精度较高,但覆盖范围有限且重访周期长。为了充分发挥两种技术手段的优势,需要探讨一种适用性好、反演精度高的主被动融合测深方法。

在卫星遥感数据源方面,被动光学遥感数据来源丰富,可以从IKONOS、Pleiades、GeoEye-1、WorldView-3、GF-2、ZY-3等系列卫星获取中高分辨率的立体像对数据[3-6]。主动光学卫星起步较晚,美国NASA在2003年发射了全球首颗对地观测的激光测高卫星ICESat[7]。后续卫星ICESat-2也于2018年发射并继续执行激光测高任务[8]。而我国2019年发射的GF-7卫星也搭载了全波形星载激光测高载荷[9]。在双介质立体摄影测量方面,文献[10]提出了一种基于高分辨率卫星多光谱立体像对的浅水水深测量方法,浅海岛礁水深反演的相对误差小于20%;文献[11]利用WorldView-2卫星影像,解决了双介质立体摄影测量折射改正算法适用性差的问题,在甘泉岛的浅海测深精度达2.08 m。在星载激光测深方面,文献[12]验证了ICESat-2的激光载荷ATLAS具备浅海测深能力,并推导了水底高程折射改正方法,试验中探测的最大水深达38 m,均方根误差小于0.6 m;文献[13]针对ICESat-2(ATL03数据)提出了一种自适应椭圆滤波测深方法,在我国南海甘泉岛和珊瑚岛开展测深试验,结果表明,测深的均方根误差分别为0.48和0.79 m。通过上述研究发现,双介质立体摄影测量水深的反演结果难以达到激光雷达测深的精度水平,其中一个原因是对水面高程估算的不确定性。

本文以我国南海浅海岛礁为例,利用ICESat-2激光测高数据和WorldView-3立体像对数据,构建主被动光学卫星遥感数据融合的测深模型,开展高精度、无实测控制点的浅海水深测量试验。

1 研究区域与数据

研究区域位于中国南海西沙群岛东部,该区域四周沙堤环绕,水体透明度高,漫射衰减系数[14](Kd)约为0.11 m-1,太阳光透水深度大于20 m,属于典型的一类水体,适合开展光学遥感水深反演试验。

被动遥感影像数据采用的是WorldView-3立体像对数据(见表1)。该卫星搭载推扫式线阵相机,影像成像模型稳定,可采集0.31 m分辨率的全色影像和1.24 m分辨率的多光谱影像。目前广泛应用的是4个波段(蓝、绿、红、近红外)的多光谱立体像对,全色光谱范围为400～850 nm,在分辨率、透水波长及影像角度上均满足双介质立体摄影测量的要求。研究区的立体像对影像为2020年9月30日拍摄,影像中有少量的云和耀斑,对水深反演结果影响较小。

表1 WorldView-3和ICESat-2卫星参数

主动激光雷达数据采用ICESat-2卫星搭载激光载荷ATLAS的二级产品ATL03,该数据产品为全球定位光子数据,记录了接收光子的经纬度、高程、激光束的采样时间等信息。ATLAS激光测高系统采用光子计数探测体制,具有微脉冲、高重频、窄脉宽的特点,激光波长为532 nm,单脉冲能量为48～170 μJ,重复频率为10 kHz,脉冲宽度为1.5 ns,具体的卫星参数见表1,能够按照沿轨方向连续获取星下点的高程[8]。研究区的ATLAS轨迹如图1所示,圆点为激光束由南向北经过研究区的一轨数据(GT1L),采集时间为2019年1月17日。由于ATLAS采用光子计数探测体制,在极大地提高探测灵敏度的同时,回波信号周围也充满大量的背景噪声,如图2所示。

图1 研究区域影像与ATLAS轨迹(20190117GT1L)

图2 ATL03数据光子点云沿轨剖面

2 研究方法

2.1 双介质立体摄影测量模型

双介质立体摄影测量是根据立体摄影测量原理,同时考虑光线在大气和水体两种介质中折线传播的特点,利用水底点与对应同名像点的几何光学关系确定水底点三维坐标[1]。光学卫星在双介质立体成像的几何关系如图3所示。(点A为摄站S1、S2垂直面上的理论交会点,点P为S1P2和S2P2反向延长线的交点,即水底点。p1、p2分别为左右图像上的像点,其中,像点p1在直线S1P1上,S1为左影像相机镜头的中心位置,P1为成像光线与水面的交点,折线S1p1P为左影像上像点p1的成像光线。同理,右影像上同名像点p2的成像光线为折线S2p2P)。

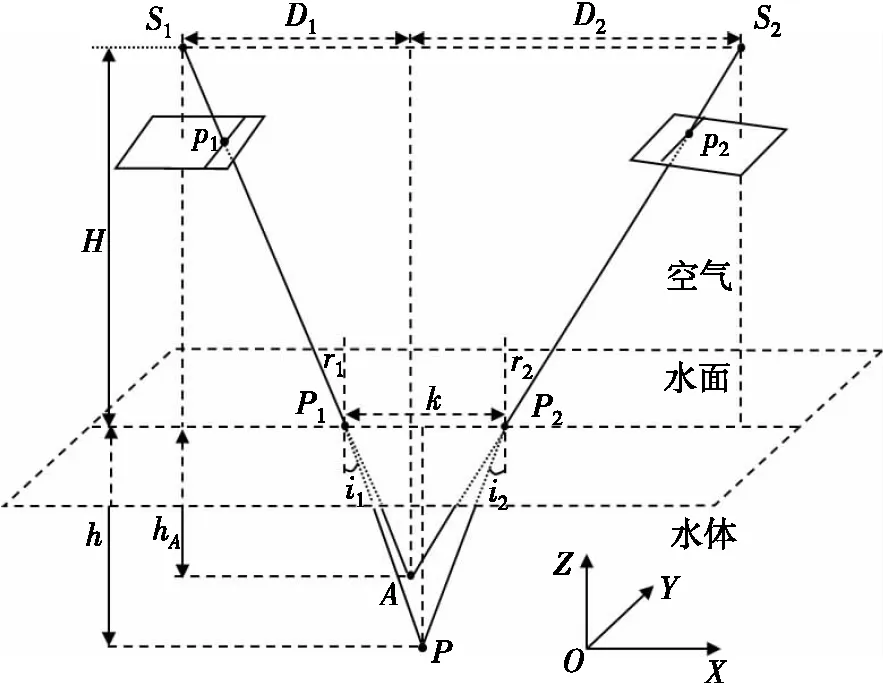
图3 光学卫星在双介质立体成像的几何结构

假设水面近似水平面,为了得到折射改正后的水深h,按照单介质摄影测量原理先求解出水面到理论交汇点A的距离hA,则有

hA=Z0-ZA

(1)

式中,ZA为理论交汇点A的高程;Z0为估算的水面高程,即水面点P1和P2的高程。一般Z0是通过识别水陆岸线内插出对应像元的高程,取平均值作为水面高程。

由于水面点的连线P1P2平行于飞行方向,水深h的折射改正由同名光线S1P2和S2P2的入射角r1和r2确定,而折射角i1和i2可根据入射角r1和r2的几何关系计算得到。设P1和P2之间的距离为k,根据同名光线的几何关系可得[15]

k=(tanr1+tanr2)·hA=(tani1+tani2)·h

(2)

式中,n为水的折射率,则有

(3)

同时考虑左右两个三角形结构,由点A垂线两侧的三角关系可知

(4)

(5)

(6)

(7)

折射角i1和i2可进一步推导为

(8)

(9)

将式(8)和式(9)代入式(3)中,双介质立体摄影测量的折射改正水深h为

(10)

2.2 激光雷达测深模型

激光雷达测深的基本原理是通过主动发射一束532 nm波长的激光脉冲,依次穿过大气、水面、水体及水底,激光探测器接收并记录该脉冲在几何路径上光子的飞行时间,通过检测水面和水底的回波信号往返的时间差,结合光速反演水深。由于ATL03中包含了大量的噪声光子,有效识别水面和水底的信号光子是ICESat-2水深反演的核心问题。假设噪声光子是随机分布的,信号光子相较于噪声光子在空间分布上更加密集。根据光子点云的离散分布特征,采用自适应椭圆滤波测深方法[13]分别提取水面光子(Zs)和水底光子(Zb)。

由于ATL03数据中地理坐标没有考虑气-水界面处折射率的变化,因此水底光子的高程需要进行折射改正。激光折射改正几何结构关系如图4所示,根据斯涅尔定律,折射角θ推导公式为

图4 激光折射改正几何结构

(11)

入水光线R和S之间的关系可表示为

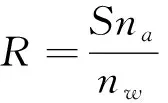
(12)

(13)

而水底光子校正前与校正后的光子之间的距离P利用余弦定理可得[12]

(14)

其中,α和β的表达式分别为

(15)

(16)

因此,在垂轨方向和垂直高程上的偏移量ΔY和ΔZ可推导为

(17)

式中,na、nw分别为空气和水的折射率;φ为激光入射角;θ为折射角,则夹角ψ=φ-θ;hA为直线传播条件下水面与水底光子的高程差;S为未折射改正的水下斜距;R为改正后的水下斜距;P为水底光子折射改正前后的距离。

由于ICESat-2几乎垂直对地观测,折射角θ的最大值为0.38°,因此,偏移量ΔY的大小可以忽略,仅计算垂直方向的折射改正量ΔZ。则激光雷达的折射改正水深公式为

h=hA-ΔZ

(18)

2.3 主被动融合测深模型

双介质立体摄影测量模型是建立在平静水面的基本假设,但实际情况中的风速、涌浪等环境要素会引起水面高程的变化,改变立体双介质中同名光线的几何结构,从而导致测深误差。而激光雷达测深模型中可以获得沿轨方向上的瞬时高程,提取的水面光子具备高程的动态范围。因此,主被动融合测深模型是将激光雷达反演的水面高程作为双介质立体摄影测量水面高程纠正的起算位置。则水面激光点到双介质理论交汇点的距离hA为

hA=Zs-ZA

(19)

此外,双介质摄影测量中海面曲率变化也会引起同名光线S1P2和S2P2的入射角r1和r2计算误差,但这部分的几何模型误差与水面高程无关。因此,在海面波浪较小的情况下,可以利用区域网平差的简单多项式拟合水深改正误差。试验采用双线性二次多项式的误差改正模型,在各点深度中加入适当的改正数δh,公式为

δh=C0+C1X+C2Y+C3X2+C4XY

(20)

式中,C0、C1、C2、C3、C4为待定系数,各待定系数对于一个局部小区域而言是常数。由式(20)可知,只需5个以上改正后的水深点作为控制点,即可以列出5个以上方程式,求解5个待定系数。在求出各待定系数后,代入式(20)可计算出各水下点的改正数,从而求得其他点的水深。

3 试验结果与分析

为了实现高精度、无实测控制点的浅海水深测量,利用WorldView-3立体像对影像范围内的ICESat-2激光点云提取水面高程,输入主被动融合测深模型,获得研究区的浅海水深反演结果。考虑研究区内的实测水深难以收集,本文将ICESat-2折射改正后的水底高程作为精度验证的参考依据。

由于ATLAS轨迹由南向北直接穿过岛礁,水面光子也被岛礁分割成南北两部分。岛礁部分的陆地光子仍需人工标记,再根据前文方法提取出水面光子的高程,结果如图5所示。需要说明的是,两个区域提取的水面平均高程为3.72 m。其中,最大高程为5.61 m,最小高程为1.82 m,且均在岛礁北部,这说明北部的风浪更大,导致水面高程相较于南部变化较大。

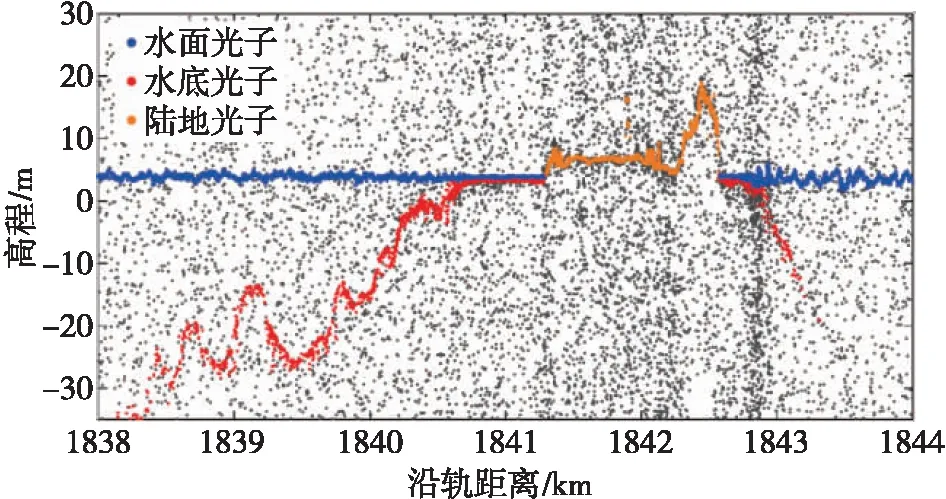
图5 水面光子提取结果

主被动融合测深结果如图6所示,地理坐标统一为WGS-84坐标系,高程采用大地高。从定性角度上看,水深结果层次分明,区域内的最大水深为22.51 m,与影像中目视透水深度基本一致。定量评估采用与激光水面高程同测线折射改正后的水底高程作为精度验证的依据。图7分别为岛礁南北两个区域激光水下点的折射改正结果,蓝色点表示水面光子,红色点表示折射改正前的水底光子,绿色点为改正后的水底光子。由于光子计数的离散特性,采用三次样条曲线获取连续的激光水底高程,拟合后的最大水深为32.13 m,能够满足精度验证的需求。

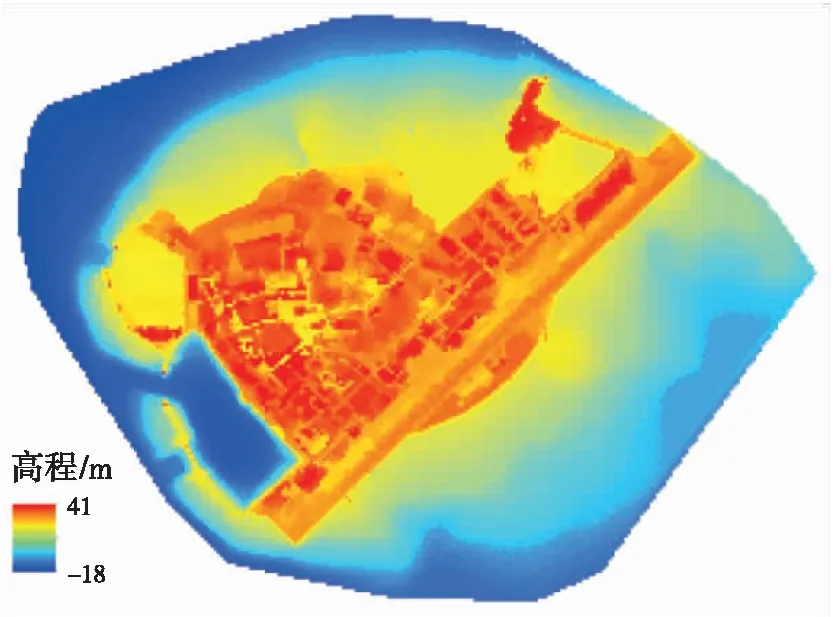
图6 主被动融合测深结果

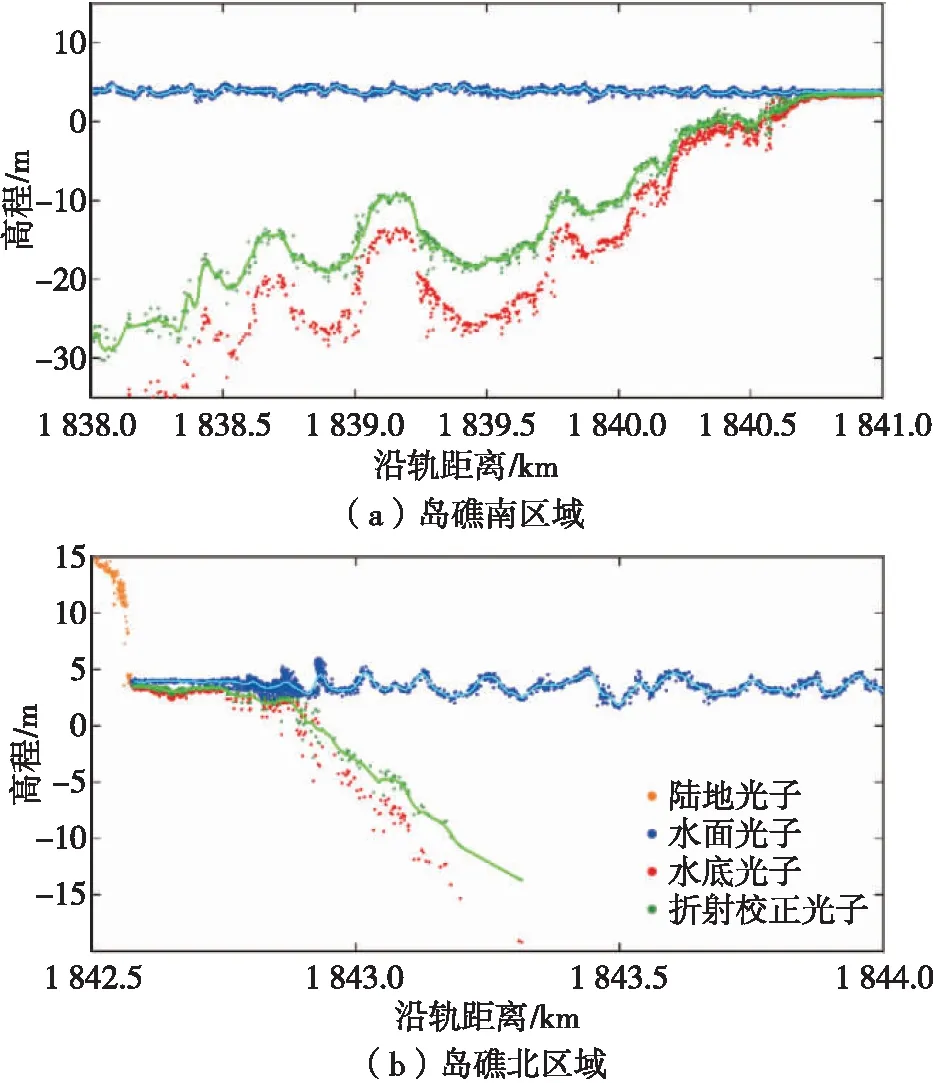
图7 激光水下点折射改正结果

将岛礁南北两个区域的主被动融合测深结果与双介质立体摄影测量结果同步比较,统计了平均绝对误差(MAE),标准差(SD),均方根误差(RMSE)和R2,结果见表2。主被动融合测深模型在岛礁南北的RMSE分别为0.69和0.28 m,而立体双介质模型的RMSE分别为0.99和2.47 m。此外,主被动融合测深模型和立体双介质模型在南部的绝对精度分别为0.48±0.50和0.78±0.61 m,在北部的绝对精度分别为0.23±0.16和2.25±1.02 m。相比之下,主被动融合测深模型的总体测深精度更高,计算的R2分别为0.94和0.98,特别是在岛礁北部的精度有显著提升。这说明该模型适用于水面高程变化较大的区域,精度上要优于传统的双介质立体摄影测量,能够有效弥补立体双介质模型水面高程不确定性带来的测深误差。

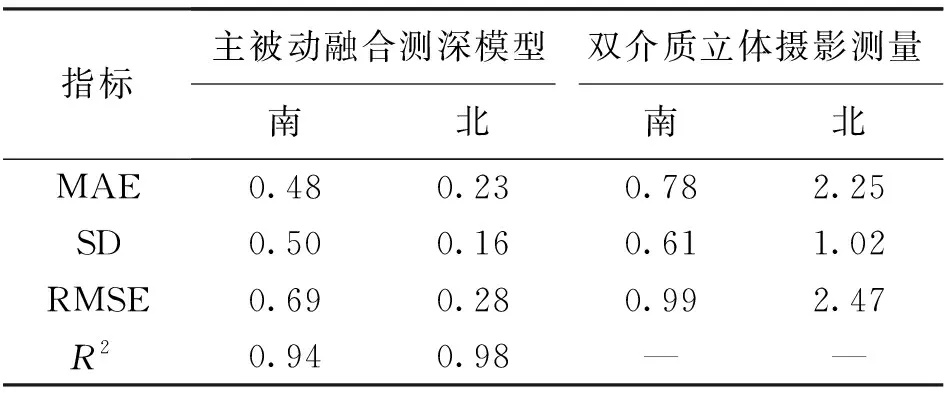
表2 主被动融合测深精度 m

4 结 论

本文基于ICESat-2激光测高数据和WorldView-3立体像对数据,对我国南海岛礁开展光学卫星遥感数据融合的浅海水深测量,得到以下结论:

(1)本文模型在研究区的RMSE分别为0.68和0.28 m,表现出较好的精度水平,能在一定程度上解决双介质立体摄影测量由于水面高程不确定带来的测深精度问题。

(2)从研究区的ICESat-2水深反演结果来看,ATLAS反演的水深能够达30 m以上,在一定程度上表现出较强的水体透射能力。

(3)由于ICESat-2激光测高数据和WorldView-3立体像对数据不一定在同一时间采集,ICESat-2反演的水面高程不一定表示WorldView-3立体像对影像中的瞬时海面。但现有的在轨卫星难以获得同一海域的时间同步卫星遥感立体影像和多波束激光雷达测深数据,建议国家研制主被动融合浅海测绘卫星,同时搭载高灵敏度、高动态范围海洋立体测绘相机和多波束海洋测深激光雷达。

综上所述,利用ICESat-2和WorldView-3主被动光学卫星遥感数据融合的浅海水深测量,结合了主被动遥感手段的特点,在技术路线上合理可行,能够实现高精度浅海遥感三维测绘,为满足浅海测绘、大区域珊瑚礁遥感调查监测、海岸带和浅海遥感地质调查的需求提供技术手段。