结合机器学习的GNSS-IR多卫星双频组合土壤湿度反演
聂士海,王 龙,王梦柯,李 鹏,梁 磊,黄丹妮,刘 斌
(1. 滁州学院地理信息与旅游学院,安徽 滁州 239000; 2. 南京信息工程大学遥感与测绘工程学院,江苏 南京 210044)
土壤湿度即土壤水分或土壤含水量(soil moisture content,SMC),在天气预报、气候研究[1]等方面有着积极响应。及时掌握区域的土壤湿度信息,可有力促进精准农业发展。可见,开展对土壤湿度的监测研究具有重要意义。
随着对GNSS卫星信号的不断研究,L波段的微波信号在遥感领域的应用引起广泛关注,从而产生了新的遥感手段GNSS-IR(GNSS interferometric reflectometry)技术[2]。随着GNSS遥感的兴起,GNSS-IR技术被广泛应用于雪深[3]、土壤湿度[4]等方面的监测,其可行性和性能已得到充分的证实。文献[5]开创了相关研究的先河,并验证了多径误差信噪比SNRMP的频率、相位、振幅这3个物理量与实测土壤湿度之间具有一定的相关性。近年来,众多学者相继进行相关研究并引入算法,如机器学习遗传算法对支持向量机进行优化[6]、深度学习算法[7]、支持向量回归机[8]等,其目的在于提高土壤湿度反演的精度。
研究表明,全球卫星导航系统搭载的L波段信号对土壤湿度较敏感,非常适合土壤温度变化监测。因此,为提升GNSS-IR土壤湿度反演预测精度,本文利用两种神经网络学习算法,即BP(back propagation)和RBF(radial basis gunction),构建土壤湿度预测模型,并与传统的一元线性回归(unitary linearity regression,ULR)模型进行对比分析。
1 GNSS-IR土壤湿度反演原理
鉴于GNSS卫星反射信号与地表环境参数具有一定的相关性,且接收机接收到的信号实际为合成信号,导致接收机接收信号数据时易产生多路径干涉效应。图1为多路径干涉效应原理。

图1 GNSS多路径误差几何模型示意
研究表明,利用SNR可实现地表环境特征的监测,且SNR观测值在低高度角时能够较好地映射出测站周围多路径效应反射物丰富的物理特性,且SNR与卫星高度角和多路径效应之间具有相应的特性[9-10]。
SNR观测值默认单位为指数单位dB/Hz。研究表明,一般需将SNR观测值进行线性化单位(Volts/Volts)转换,公式[11]为
SNR=10SNRdB-Hz/20
(1)
假设只发生一次反射基础上,干涉效应使接收机接收到的SNR中包括直射信号和反射信号,可表示[5]为
(2)
式中,Ad、Am分别为直、反射信号的振幅;ψ为延迟相位。鉴于多路径直、反射分量数值上的差异,即Ad≫Am,加之SNR随GNSS卫星高度角发生变化时Ad、Am和ψ均会发生变化,会造成SNR波动,且SNR整体呈二次曲线变化的趋势[12]。
根据式(2),SNR的反射分量可用余弦函数模型近似表示为
(3)
式中,SNRMP为反射信号;Am为反射信号的振幅;H为天线高;θ为卫星高度角;λ为波长;φ为延迟相位。
令t=sinθ,f=2H/λ,则式(3)可简化为标准的余弦函数,公式为
SNRMP=Amcos(2πft+φ)
(4)
图2为本试验站点P037测站G09卫星(DOY:2017-200,GPST:09:00:45—15:12:45)L1、L2频点上对应的合成信噪比观测值S1、S2随卫星高度角的变化趋势。可以看出,L2载波上的SNR观测值整体小于L1载波上的SNR观测值。
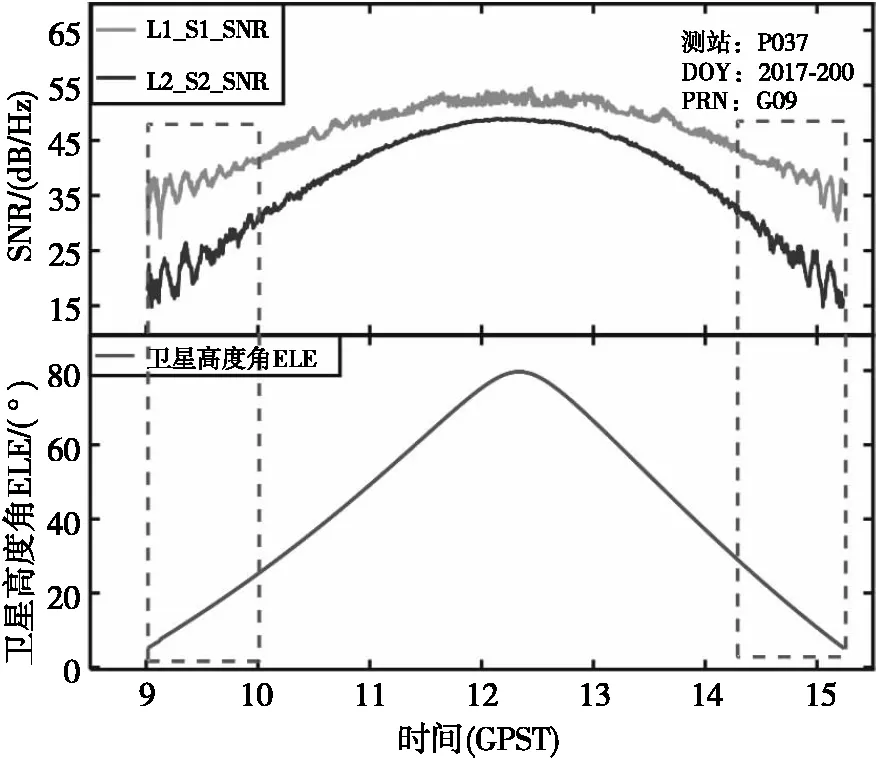
图2 SNR观测值随卫星高度角变化特征
图3为G09卫星L1、L2频点对应的去趋势项后的SNRMP重采样图。可以看出,SNRMP呈明显的周期特性,且GNSS卫星处于低高度角时,SNRMP的周期性更为明显。因此本文将卫星高度角均限制在5°~30°之间,把该高度角范围在5°~30°之间的SNR观测值作为研究对象。
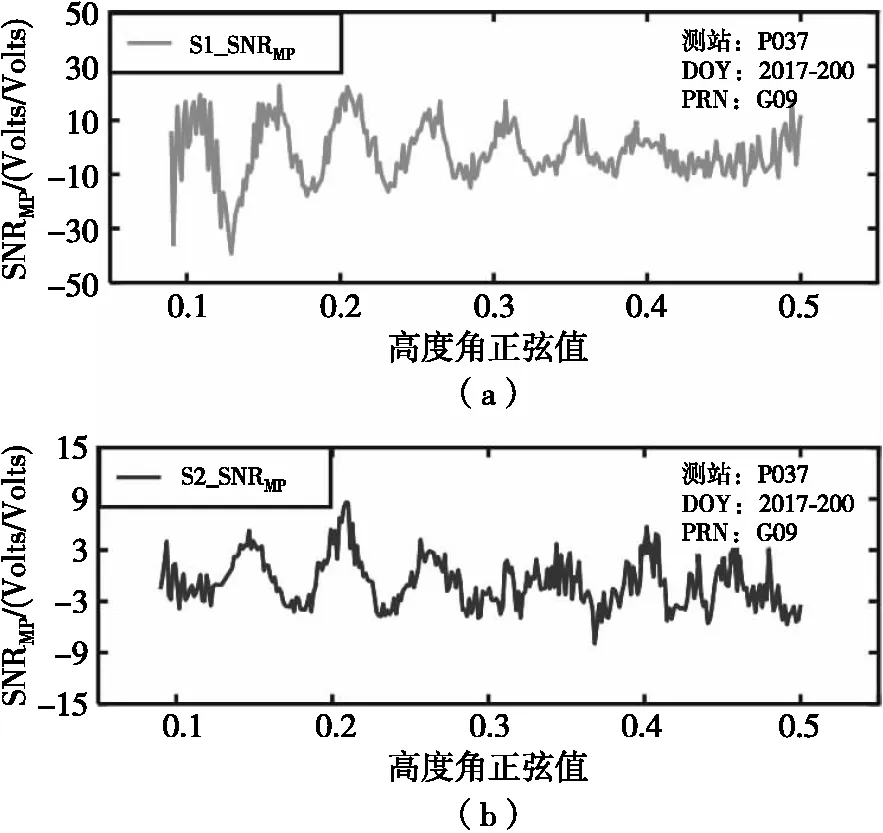
图3 去除趋势项后的SNR残差序列
2 试验站点数据
2.1 测站和数据源
选择PBO(Plate Boundary Observation)网络提供的P037测站2017年7月8日—8月6日(DOY:2017-189—2017-218)共30 d的观测数据进行试验,且测站均安装有大地测量型GNSS接收机,能够记录GNSS卫星多频点上的SNR观测数据。P037测站的具体参数见表1。

表1 测站点P037的具体参数
测站地理位置及周围环境如图4所示。可以看出,测站周边地形较为平坦、开阔,且植被稀少无遮蔽,整个试验期间可视为裸土,有利于土壤湿度监测。

图4 测站地理位置及周围环境
土壤湿度参考值及降水量由PBO提供,且与GNSS观测数据时间段相对应,如图5所示。其中,土壤湿度及降水量均以天为单位,土壤湿度则是对8个或更多卫星轨道的土壤湿度反演结果取平均值,作为测站附近有效监测范围内的土壤湿度参考值。可以看出,试验期间P037测站出现明显降水超过5 mm的有7 d,超过10 mm的有5 d,其中DOY为2017-211的降水量最高,达23.9 mm。降水较频繁的期间,土壤湿度变化图波动较为剧烈,呈一定的非线性和随机性变化。即降水时,土壤湿度升高;降水停止后,土壤湿度逐渐降低。可见,降水是影响土壤湿度变化的主要原因,且本文选取P037测站的降水量均较为丰富,适合开展土壤湿度变化研究。
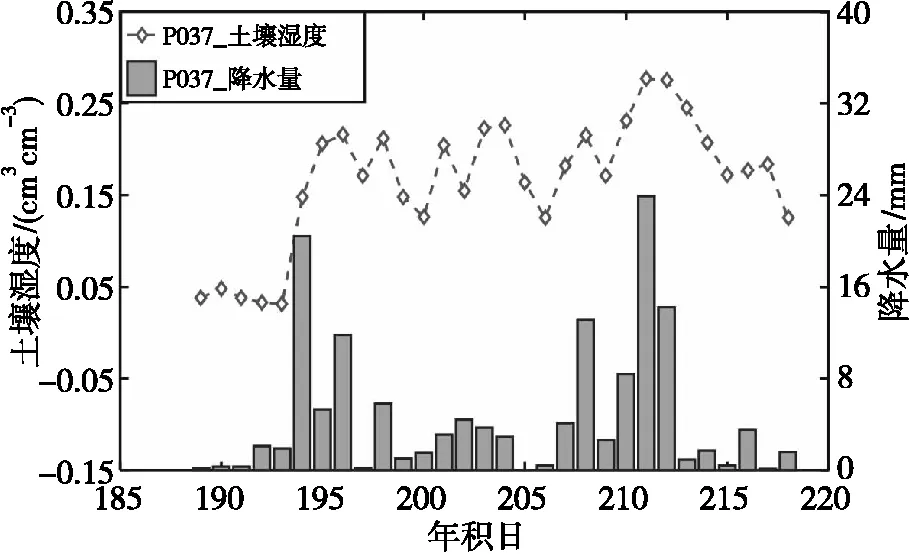
图5 试验期土壤水分降水
2.2 有效卫星的选取
研究表明,最大功率谱密度能够在一定程度上表征多路径误差信号的质量[13-14],因此可采用L-S频谱分析选取出卫星信号质量较好的GNSS卫星。L-S频谱分析后主导频率的功率应至少是次主峰频率功率的两倍[15]。图6为P037测站(DOY:2017-200)不同卫星频谱分析图。其中,图6(a)、(b)分别为G09卫星L1、L2波段上SNRMP的频谱分析图;图6(c)、(d)分别为G14卫星L1、L2波段上SNRMP的频谱分析图。

图6 GNSS卫星L-S频谱分析
可以看出,图6(a)、(b)满足主导频率的功率至少应是次主峰频率功率的两倍的条件,且进一步说明卫星数据的质量较好,在选择卫星时,保留这类卫星;图6(c)、(d)则缺乏任何主导频率,这可能会在后续的参数估计中引入显著的误差,从而对结果产生影响,加之不满足上述条件,且反映出卫星数据的质量较差,因此,在选择卫星时,舍弃这类卫星。
2.3 试验数据处理
本文选取的卫星高度角限制在5°~30°之间,在进一步考虑信噪比误差进行卫星选择后,每天选取8个时段。由于白天土壤湿度变化较大,对日土壤湿度影响权重较晚上大,因此,白天选取6个时段,晚上选取2个时段。虽然一天中低卫星高度角多路径误差对应持续时间约为1 h,造成在低高度角时可用GNSS卫星甚至更少。因此,每次观测时段只选择一颗GPS卫星,将逐小时的SNR观测值作为本文研究的数据源。
结合机器学习的GNSS-IR多卫星双频组合土壤湿度反演流程(如图7所示),具体过程如下。
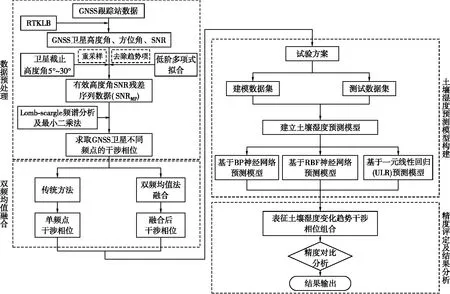
图7 土壤湿度反演流程
(1)GNSS跟踪站数据的获取。利用GNSS卫星o文件和n文件,获得SNR、卫星高度角、方位角等数据。
(2)观测数据的前处理。选取GNSS卫星高度角在5°~30°范围的L1、L2频点上的SNR观测数据,并对SNR数据进行前处理。



(6)数据划分。将数据划分为训练集和测试集。
(7)ULR模型的构建与验证。依据求解出的延迟相位和土壤湿度观测值构建ULR模型,并进行结果验证分析。
(8)基于机器学习算法建模并验证。基于BP、RBF两种神经网络算法,对求解出的延迟相位进行预测模型构建,并进行结果验证。
3 试验分析
依据上述原理及方法,通过平差求解出延迟相位,每个观测时段可以计算出一个延迟相位,一天内可依据8个观测时段计算出8个延迟相位,并对其取平均值,将该平均值作为日延迟相位。以每日时间尺度,分别对L1波段上SNRMP和L2波段上SNRMP进行计算,得到对应的日延迟相位,并分别绘制L1、L2频点和L1、L2均值融合后的土壤湿度与延迟相位时间变化趋势(如图8所示)。可以看出,延迟相位和土壤湿度之间的总体变化趋势具有较强的一致性,且土壤湿度与L1、L2均值融合后、L2频点和L1频点所求得的延迟相位间的相关系数分别为0.956、0.937、0.918,表现为强相关。

图8 延迟相位与土壤湿度趋势变化
为进一步验证延迟相位与土壤湿度的关系,构建ULR分析模型如图9所示,回归残差如图10所示。可以看出,ULR模型预测出土壤湿度与参考值间偏离度较小,回归残差较小。引入F检验,经查表F0.005(1,28)=9.28,经F检验,3种方法的F检验量均大于F0.005(1,28)=9.28,可见回归效果显著,体现出延迟相位与土壤湿度之间有较强的线性相关性,说明可利用延迟相位反演出高精度的土壤湿度信息,即基于延迟相位对土壤湿度进行反演研究。

图10 土壤湿度线性回归残差
为评价基于机器学习GNSS-IR多卫星双频组合的土壤湿度反演性能,将数据源的前70%作为训练集,后30%作为测试集,设置9种方案进行土壤湿度反演试验,见表2。
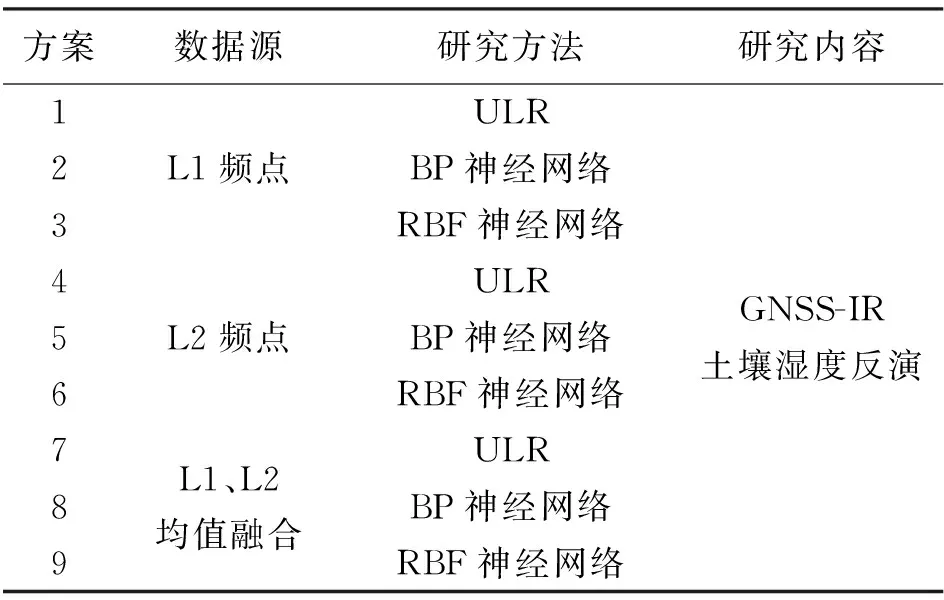
表2 土壤湿度反演试验的方案
依据9种方案分别构建土壤湿度预测模型,并对各模型结果进行对比分析。模型预测值与土壤湿度参考值之间的对比如图11所示。

图11 预测值与实测值间对比
可以看出,土壤湿度的预测值与参考值之间的变化趋势大体一致。为体现土壤湿度预测效果,针对上述9种方案,分别求解对应的预测残差值,并绘制残差图,如图12所示。
可以看出,3种模型土壤湿度预测值的残差可见,BP、RBF模型的土壤湿度预测残差比ULR小,体现出BP、RBF模型优于ULR模型,为更好地描述其性能,统计结果见表3。
4 结 语
本文在分析GNSS测量多路径误差产生机制和神经网络的机器学习基础上,提出了一种基于机器学习GNSS-IR多卫星双频组合的土壤湿度反演方法。利用P037测站的GPS卫星L1、L2频点上的SNR观测值与土壤湿度数据进行土壤湿度反演研究,并利用BP、RBF神经网络构建相应的土壤湿度预测模型,与ULR预测模型进行对比分析。结果表明,由SNRMP求解出的延迟相位与土壤湿度间存在较强的相关性,L1、L2双频融合反演结果与土壤湿度的相关系数为0.956,均优于L1、L2频点反演结果,且L2频点反演结果优于L1。同时,BP和RBF神经网络模型预测结果精度均优于ULR模型,其原因可能是土壤湿度易受植被覆盖、土壤温度、空气湿度等多种影响因子的共同作用,且多路径反射并非假想的镜面反射,导致采用简单的一元线性回归模型很难表征延迟相位与土壤湿度间的非线性的特征。此外,神经网络算法能够修正弱化土壤粗糙度导致的介电常数不同,对地表起伏、土壤粗糙度及植被等的影响具有一定的抑制作用。
致谢:感谢美国PBO观测计划提供的GNSS、H2O和UNAVCO数据;感谢科罗拉多大学提供的土壤湿度对比分析数据。

