分布式驱动地面无人平台直接横摆力矩控制研究

谭森起，汪洋，罗天，张乃斯，李胜飞，潘博，崔星

（中兵智能创新研究院有限公司，北京 100072）

1 引 言

分布式轮毂电机驱动系统中的各驱动电机均可独立按需控制，因此更易于实现驱动防滑控制、直接横摆力矩控制以及防侧翻控制等操控稳定性控制功能，进一步提升电动无人平台的稳定性和越障机动能力。然而，同时多个电机独立控制增加了整车控制系统的复杂程度，给车辆动力学控制带来了一定挑战［1-3］。

国内外专家学者针对如何提升分布式驱动车辆的操纵性能和横向稳定性进行了诸多研究。其中，最常见的方法是通过直接横摆力矩控制（Direct Yaw-moment Control，DYC）方法，对车辆的横摆角度和质心侧偏角进行跟踪，获取需求的横摆力矩并分配至各轮胎，以提升车辆的横向稳定性。文献［4］针对6×6分布式驱动平台提出一种DYC控制方法，提升多轴车辆在复杂转向工况下的行驶稳定性。文献［5］提出一种双层级联控制框架用于计算4×4分布式驱动车辆的需求直接横摆力矩，用于车辆的横向稳定性控制。为了进行系统状态误差补偿，文献［6］提出一种基于稳态状态观测器的DYC控制方法，改善了四轮分布式驱动车辆的操纵稳定性。文献［7］针对过驱动系统引入控制分配理论，结合非线性滑模变结构控制与二次规划方法，提出一种双层控制架构，提升分布式驱动车辆极限工况下的稳定性裕度和通过速度。针对分布式电驱动车辆在加速转向工况下车轮驱动力矩的控制分配问题，文献［8］提出一种对参数不确定和模型误差鲁棒性较强的分层控制策略，以提高车辆操纵性和降低电能损失为目标，对控制器性能进行优化设计。文献［9］结合差分（Proportional Integral Derivative，PID）控制理论与序列二次规划优化方法，构建了双回路嵌套DYC控制框架，对分布式电驱动车辆控制稳定性进行提升。文献［10］基于模糊控制思想及专家规则方法，对于多轮电驱动装甲车辆进行直接横摆力矩控制，显著提升了车辆在极限工况下的目标跟踪性能。文献［11］基于线性二次规划控制理论，研究了四轮分布式电驱动车辆的横摆稳定性，并通过双轮控制模式进行转矩分配，实现了四轮驱动电动汽车的稳定性控制。文献［12］设计了一种8×8分布式电驱动轮式装甲车辆直接横摆力矩与转矩矢量控制分层控制框架，实现8×8车辆的直接横摆力矩控制。实时仿真测试结果表明，该控制方法能合理分配车轮转矩，有效控制横摆角速度，提高车辆的行驶稳定性。文献［13］为提升分布式电驱动车辆在极限越野环境下的高速避障能力和操纵稳定性，提出一种充分考虑车辆过弯姿态反馈的分层协调横向稳定性控制方法。实验结果表明，该分层协调控制策略具有较强的车身姿态修正能力，可以提高车辆的路径保持精度和过弯横向稳定性。

上述算法设计主要针对前轮转向车辆，且在载荷分配算法中，未考虑轮胎载荷利用率对控制稳定裕度的影响。本文针对后轮转向8×8独立驱动无人平台越野机动的行驶稳定性需求，充分考虑后轮转向带来的转向不足特性，建立了面向控制的整车动力学模型，进而提出一种分布式独立驱动无人平台驱动扭矩优化分配分层控制方法。上层控制器用于求解无约束下的需求驱动力矩和横摆力矩，下层控制器用于基于控制稳定性的各轮胎扭矩分配，实现了各轮胎驱动力基于垂直载荷利用率和跟踪控制精度的优化分配。最终通过Simulink和TruckSim联合仿真实验，验证了在该控制策略下，分布式驱动平台越野机动过程中的控制稳定性和越野机动性均得到一定程度的提升。

2 整车模型构建

某8×8独立驱动无人平台驱动系统结构如图1所示，采用电传动加轮毂电机独立驱动以及后轮转向布局形式。柴油机以恒定功率带动发电机运转，为蓄电池补充电能，蓄电池经由DCDC转换器及电机控制器向8个轮毂电机供电。

图1 目标车型驱动系统布局示意图Fig.1 The drive system configuration scheme

为实现无人平台的越野机动集成控制，充分考虑后轮转向机构的转向不足特性，基于控制需求及硬件处理器计算能力，对车辆模型进行简化，构建面向控制的分布式驱动整车动力学模型。在该模型中，假设轮胎特性处于线性区域，轮胎侧向力与侧偏角呈正比，忽略行驶阻力的影响，忽略转向系统、悬架系统的影响，综合考虑车辆纵向运动、侧向运动和横摆运动。首先，建立21自由度车辆线性参考模型，如图2所示。该模型主要包括8个独立驱动轮胎的横向、纵向运动16个自由度，车体纵向、侧向和横摆3个自由度，以及后桥2个转向轮的2个转向自由度。图中，v代表车辆运动方向，vx、vy分别代表车辆纵向和横向速度，Mz表示车辆的横摆力矩，Fxli、Fyli、Fxri、Fyri（i=1，2，3，4）代表第i轴左右轮胎的横向力和纵向力，li表示第i轴到质心的距离，δrs代表后轮的转向角。

图2 动力学分析示意图Fig.2 Schematic diagram of dynamic analysis

根据以上分析，车辆纵向加速度与纵向力的关系可以表示为

式中，m为整车质量，r为车辆的横摆角速度。同时，车辆侧向加速度与侧向力的关系表述为

此外，车辆的横摆角加速度与横摆力矩之间的关系可以表示为

基于小角度侧偏角的假设，后轴转向轮的侧偏角可以近似表示为

同时，其余三个非转向桥上的轮胎（j=1，2，3）的侧偏角可近似为

进一步地，基于局部线性近似假设，各轮胎的侧向力可以表示为

从而可以进一步简化控制模型，基于转向角小角度假设并忽略左右轮胎侧向力差异，选取侧向速度vy及横摆角速度r作为状态变量，简化后的面向控制的整车动力学模型可以表示为

式中，δdm是直接横摆力矩的等效转向角数值。

3 级联扭矩分配控制器设计

该8×8的驱动力矩分配分层控制策略框架如图3所示。该控制框架主要分为两层，在上层控制器中，利用实际车速、车辆位姿信息及路径信息，对车辆横纵向运动状态进行调整，获得维持车辆运行状态所需的纵向力矩及横摆力矩数值；在下层控制器中，利用其横纵向扭矩需求、轮胎负荷率与跟踪效果控制，对每个驱动轮进行驱动力矩的优化再分配。

图3 分层控制器结构框图Fig.3 Diagram of the overall control scheme

3.1 上层控制器设计

考虑到控制的鲁棒性以及应用的可行性，上层控制器主要采用两个PID控制器通过纵向速度误差和航向角误差，对车辆的横纵向运动状态进行控制，而将物理约束、车辆非线性特性等复杂特性、边界条件等计算流程下放至下层分配控制器。

其中，纵向控制是一个以纵向速度偏差为输入的PID控制器

式中，Kpv和Kiv分别是比例增益系数和积分增益系数，vxref是纵向参考速度。同理，横向位置控制是一个融合角度偏差为输入的PID控制器［14］

式中，θeref为等效参考融合偏差角，θe为等效融合偏差角计算值。

由于后轮转向带来的转向不足特性，仅靠转向角难以实现灵活转向。因此，在求解出需求转向角δd之后，需进一步计算需求的直接横摆力矩，此处直接横摆力矩的介入强度采取高阶平滑多项式来进行计算

式中，∆=abs（δrs/δmax），δmax为最大机械转向角，Tdmax为设定的最大直接横摆力矩介入值。

3.2 下层控制器设计

下层控制器主要功能在于利用上层控制器的计算结果，充分考虑车辆自身物理特性约束条件，结合路径跟踪控制误差及轮胎负荷利用率对各轮胎驱动扭矩进行优化分配，提升无人平台的越野机动能力和控制稳定裕度。

下层控制器以分配误差和控制性能混合最优为目标，通过轮胎扭矩优化分配，降低扭矩分配误差及轮胎总负荷率，因此，总的目标函数可以概括为分配误差子目标函数J1与总负荷率子目标函数J2的加权分配，

式中，u为控制输入，即8个驱动电机的扭矩输出值

系数矩阵B为效能矩阵，

控制输出需求期望矩阵vd为

W1，W2为目标函数加权系数矩阵

优化过程采用二次规划算法进行求解，获取驱动轮胎的最优扭矩分配结果。优化过程充分考虑轮胎摩擦椭圆、电机输出极限以及电机响应速度等约束条件。其中，轮胎摩擦椭圆约束条件可以表示为［15］

忽略轮胎纵、侧向刚度的差别，假设车轮滚动半径为R，可进一步将轮胎力的摩擦椭圆约束转化为轮毂电机输出转矩约束，可以表示为

而电机的输出特性及响应特性等约束条件可以表示为

4 仿真验证与分析

4.1 仿真环境构建

为了验证所提出的分层控制器的控制收敛速度和鲁棒性，本文基于TruckSim和MATLAB/Simulink构建了无人平台越野机动的联合仿真环境。

在该联合仿真系统框架下，8×8无人平台的控制器利用MATLAB/Simulink进行建模，越野道路工况及整车动力学模型采用的是TruckSim中的自定义环境及车辆模型，如图4所示。其中，整个越野工况为半径100 m的环形路工况，为了能够验证分层控制器在不同工况下的适应能力，将仿真环境设定为平台路面环境、崎岖路面环境、上下坡环境及变附着系数路面环境四部分。其中，在平坦路面区间，无人车以匀加速行驶为主，最高车速为40 km/h；崎岖工况路面起伏剧烈，车辆主要以匀速行驶为主；上下坡区间最大爬坡度为12%，具体道路坡度变化趋势如图5所示；变附着系数路面主要以加减速运动为主，四种工况环境在环形越野路上分布情况如图6所示。整车动力学模型参数参照的是中国北方车辆研究所设计的一款基型无人机动底盘，其主要性能及尺寸参数如表1所示。

表1 无人平台关键仿真参数表Table 1 The key parameters for the simulation

图4 不同越野道路场景展示Fig.4 Different off-road scenarios

图5 越野场景相对高度变化Fig.5 The ground elevation of the scenario

图6 越野道路工况划分示意Fig.6 The off-road surface geometry partition

4.2 仿真结果分析

为了验证所提控制算法的控制效果，本文仿真研究中，将所提出的分层扭矩优化控制算法与扭矩直接分配算法进行路径跟踪效果对比，整体跟踪效果展示如图7所示。图中，REF代表参考路径的轨迹，后缀“_O”代表本文所提出的分层扭矩分配优化控制算法，后缀“_E”代表直接扭矩分配算法。

图7 不同算法路径跟踪效果整体对比Fig.7 The tracking overall comparison

结合图8中的路径横向跟踪误差图，分析得出，在相对平坦的平路、上下坡、变附着道路环境下，外界扰动较小，两种算法的跟踪精度均有所改善，所提算法和对比算法的误差值分别小于0.1 m和0.15 m，跟踪效果均能满足控制需求。而两种算法的最大误差均发生在崎岖路段，分析原因在于路面起伏波动剧烈，对车辆自身姿态调整产生较大的横向阻力，影响了车姿的及时调整，造成较大的跟踪误差。在此种情况下，所提算法的最大跟踪误差是0.6 m，而对比算法由于横摆力矩产生不及时，导致最大横向跟踪误差大约为1.25 m。由此可见，在极端复杂越野工况下，所提扭矩优化分配算法仍能够较好完成扭矩分配，提高无人平台的路径跟踪控制精度。

图8 不同算法路径横向跟踪误差对比Fig.8 The tracking error comparison

进一步的对比中，为了探究所提算法在车辆控制及轮胎附着力利用率优化配置方面的性能表现，对仿真过程中的车辆姿态及轮胎垂向载荷分布进行了深入对比分析，如图9～13所示。图9主要对比了两种不同控制算法下的轮胎驱动力矩分配结果，其中，“L_E”和“R_E”分别代表了直接扭矩分配算法框架下无人平台左右两侧平均分配的轮胎驱动力矩，“Li_O”和“Ri_O”分别代表了分层控制框架下左右两侧第i个轮胎的扭矩分配结果。结合图10中各个轮胎侧向力受力情况及图11的各轮胎垂向力大小，可以看出，采用直接扭矩分配方式时，轮胎驱动力大小与轮胎的负荷状态无直接关系，从而会导致在某些特定工况下，不同轮胎的附着力利用率分配不合理，部分轮胎附着力利用率过低，而部分轮胎接近附着力极限，降低了车辆的稳定裕度，影响无人平台越野机动能力的提升。而采用本文所提的优化算法，控制器根据各轮胎的受力情况，实时优化轮胎的驱动力分配，使得轮胎的横向力和侧向力分配更加均衡，峰值受力大小相较于对比算法降低了约8%，提高了轮胎附着力的利用率，增加了车辆稳定裕度，从而能够提升平台的越野机动能力。

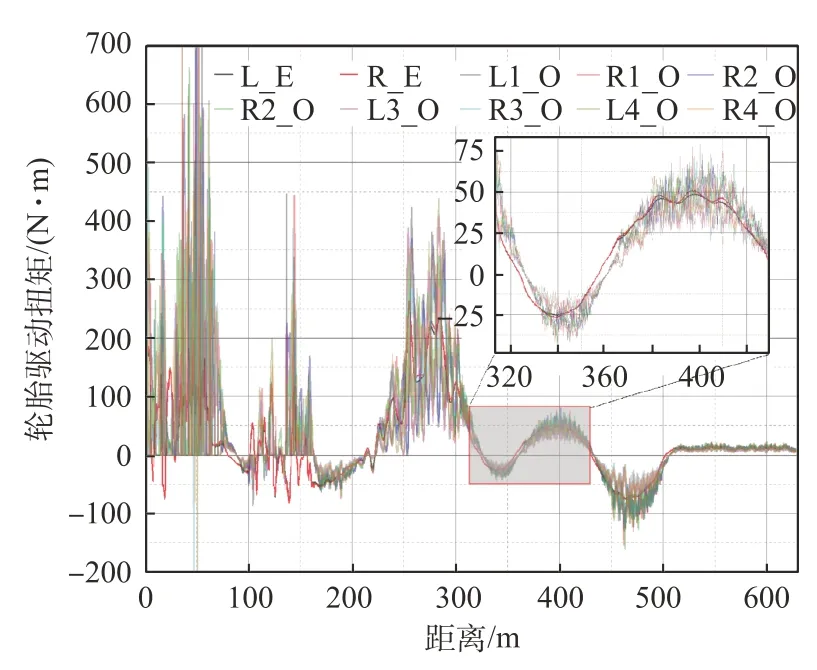
图9 不同算法轮胎驱动力矩分配对比Fig.9 The comparison of tractive torque allocation

图10 不同算法轮胎侧向力对比Fig.10 The comparison of lateral forces

图11 不同算法轮胎垂向力对比Fig.11 The comparison of veritical forces

图12 不同算法车辆俯仰姿态对比Fig.12 The comparison of pitch status

图13 不同算法车辆横滚姿态对比Fig.13 The comparison of roll status

5 结 论

本文提出一种适用于采用后轮转向的8×8独立驱动无人平台越野机动控制的驱动力矩分配级联控制方法，设计了分层控制器结构，实现了以跟踪控制误差及轮胎附着力利用率为优化目标的轮胎驱动扭矩优化分配。在所提控制器中，上层控制器用于总需求驱动扭矩和横摆力矩求解，下层控制器基于轮胎负荷及跟踪误差状态，对各驱动轮扭矩分配进行优化求解。进而，利用Simulink与TruckSim联合仿真平台，构建越野自主机动仿真场景，对所提出的控制方法进行验证。仿真结果表明，与平均扭矩分配控制的车辆相比，在所提扭矩优化分配控制策略作用下，车辆具有更好的响应特性，提高了行驶稳定性并实现了更好的路径跟踪效果。后续研究中，将聚焦算法实时性优化提升，并基于样机平台完成算法的实车部署与测试。