铝合金轮毂弯曲疲劳寿命预测*

刘 娜 刘 鹏 高媛媛

（山东建筑大学 山东 济南 250101）

引言

汽车构件的安全性一直是科研工作者关注的重点，其中轮毂的疲劳寿命是重中之重。弯曲疲劳寿命作为轮毂安全性验证方法的一种，国内外学者对其研究较为深入。陈继刚等[1]通过对3 种力学模型的研究及试验验证，发现轮毂材料以及加载轴对最大应力的影响不大，且要考虑螺栓预紧力。边雷雷等[2]利用名义应力法和FE-SAFE 软件对轮毂疲劳寿命进行了预测，结果表明，轮毂通风孔处的寿命较短。张响等[3]对比不同的损伤公式，发现用Simth-Waston-Topper 方法预测铝合金轮毂弯曲疲劳寿命较准确。P.Li 等[4]通过量化影响疲劳行为的关键因素之间的相互作用，证明了孔隙大小和加载水平都对疲劳行为有显著影响。R.Shang 等[5]根据轮毂疲劳寿命试验结果，提出了增加轮辐厚度可提高轮毂的疲劳寿命，并对优化的轮毂进行了试验验证。本文利用模拟仿真方法对某铝合金轮毂进行了静力分析及弯曲疲劳寿命预测。

1 轮毂弯曲疲劳试验原理

根据GB/T 5334-2005《乘用车车轮性能要求和试验方法》[6]规定，轮毂弯曲疲劳试验方法分为2 种：其一为轮毂在固定不变的弯矩下进行旋转，如图1所示；其二为轮毂固定不动，承受一个旋转的弯矩，如图2 所示。试验样品应是全新轮毂，每个轮毂只能做一次试验。

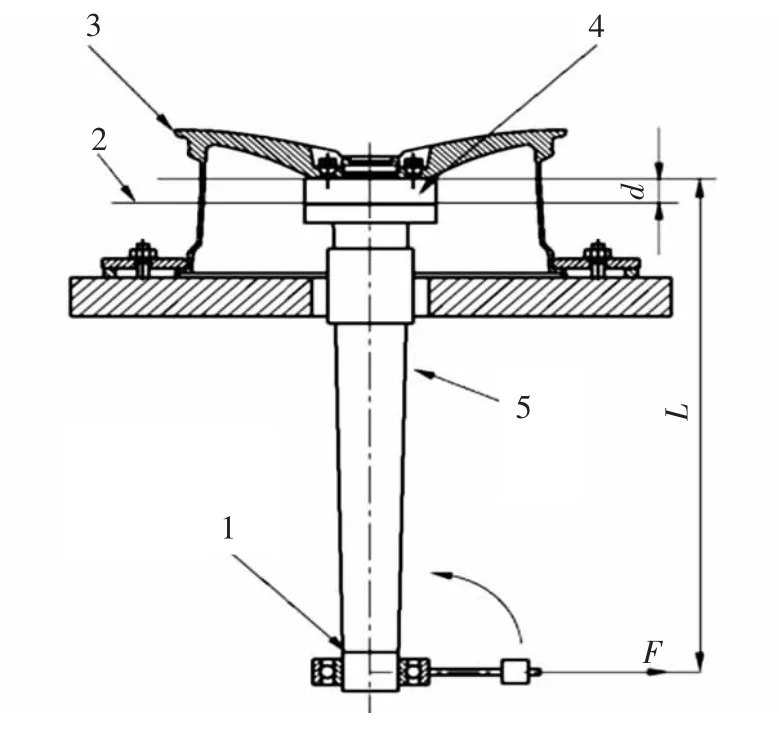
图1 试验方法1 简化图

图2 试验方法2 简化图

在进行铝合金轮毂弯曲疲劳寿命试验时，方法2，即轮毂固定不动，承受一个旋转的弯矩的加载方式更贴近实际情况。因此，选定方法2 为理论模型。

弯曲疲劳试验循环次数要求见表1[6]。

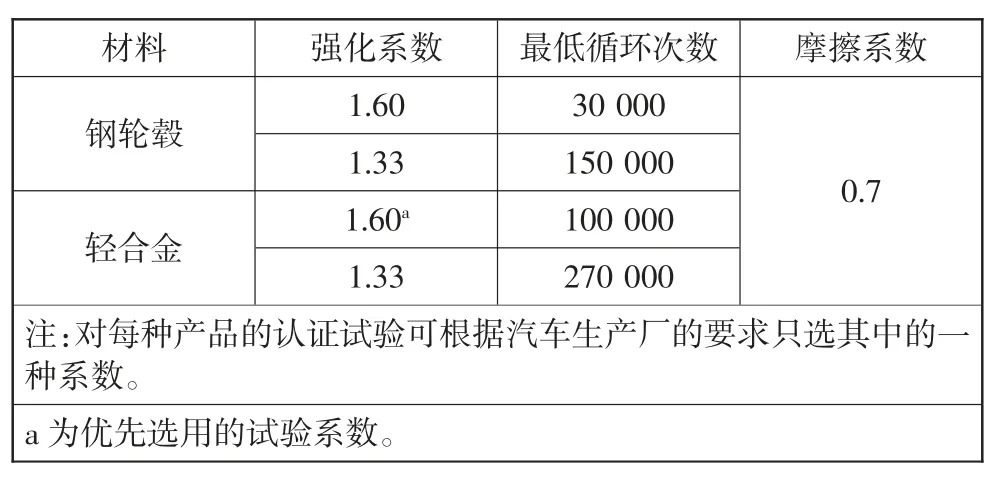
表1 弯曲疲劳试验循环次数要求

试验弯矩的计算公式如下：

式中：M 为试验弯矩，N·m；μ 为轮胎与路面之间的摩擦系数，见表1，取0.7；R 为轮胎静负荷半径，m；d 为轮毂内偏距，m；FV为轮毂额定载荷，N；S 为强化系数，见表1，其数值选择优先选用的试验系数，取1.60。

则轮毂轴端载荷为：

式中：F 为轮毂轴端载荷，N；L 为力臂长度，m。

轮毂型号为255/50R19 107W，根据轮毂型号以及材料参数，轮胎静负荷半径R 为0.70 m，轮毂内偏距d 为0.037 m，力臂长度L 为0.78 m，轮毂额定载荷FV为9 555 N。通过公式（1）和公式（2）计算，可得轮毂轴端载荷F 为6 311.7 N。

2 螺栓预紧力

在进行试验时，轮毂通过螺栓与加载轴连接在一起。选用螺纹为M14×1.5 的螺栓，该螺栓的转矩达到150 N·m。螺栓预紧力可通过下述公式求得。

普通螺纹力矩：

螺栓轴向载荷：

螺纹中径：

升角：

当量摩擦角：

式中：螺栓材料为45 钢；f 为螺母支承面摩擦系数，取0.3；d 为螺栓的螺纹大径，为14 mm；d2为螺栓的螺纹中径，mm；ρv为螺纹升角，°；λ 为螺纹当量摩擦角，°；n 为螺纹头数，n=1；p 为螺距，为1.5 mm；β 为普通螺纹的牙型斜角，为30°；T1为螺栓转矩，为150 N·m；FQ为螺栓预紧力，N。

将数据代入上述公式，可得FQ为27 708 N。

3 有限元分析

符合材料为线性材料、载荷为静态载荷、变形需为小变形3 个条件才能在结构分析中用线性静力学分析。因此，在进行有限元分析时，要将动态载荷转化为静态载荷。

3.1 轮毂材料属性及模型简化

本文研究用轮毂型号为255/50R19 107W，额定装载质量为975 kg，材料为A356 铝合金。该铝合金材料为三元素合金，能够满足轮毂的强度要求[7]。由于轮胎材料结构十分复杂，在进行有限元分析时会涉及到非线性问题，所以，进行轮毂有限元分析时，只需要对轮毂模型进行分析。对轮毂模型进行适当的简化，能提高网格划分的便捷性和网格质量，从而保证仿真计算的真实性。

轮毂的简化模型如图3 所示。

图3 轮毂简化模型

轮毂的材料属性见表2。

3.2 网格划分边界条件设置

对轮毂进行网格划分时，网格尺寸设置为6 mm，相关性设置为30，跨距角中心与关联中心设置为Medium。轮毂网格模型如图4 所示。

图4 轮毂网格模型

平均网格质量为0.72，网格质量Element Metrics图如图5 所示。图5 中，Tet10 表示10 个节点的四面体单元。

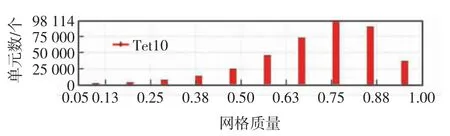
图5 Element Metrics 图

网格质量是单元的最短边与最长边的比值，理想单元的网格质量为1。从图5 可知，网格质量大于0.65 的数量超过70%。所以，该网格下的力学分析结果有效。

3.3 边界条件的施加

根据试验方法2，轮毂固定不动，轮辋外侧固定在试验台上。因此，在该位置添加固定约束[8]。

加载轴的末端受到一个弯矩，该弯矩等效为轮毂轴端载荷。将轴端载荷分解为Z 方向和Y 方向的分力，如图6 所示。2 个分力为余弦和正弦的方式加载，通过改变分力的大小来改变轴端载荷的方向。

图6 分力简化模型

轮毂边界条件施加如图7 所示。

图7 轮毂边界条件施加

为了进行静力学分析计算，在有限元分析过程中，把动态载荷转化成静态载荷[9]。本文采用12 个载荷序列来模拟轮毂在弯曲试验过程中一个完整的循环过程，将轮毂平均分为12 份，每隔30°进行一次计算。

载荷序列设置如图8 所示。

图8 载荷序列设置

3.4 有限元分析结果

材料流动破坏的主要原因是形状改变。轮毂弯曲疲劳试验中，主要以疲劳破坏为主，利用第4 屈服准则来进行分析比较合适[10]。运行完12 步载荷序列以后，提取有限元分析结果中的应力及变形。其中，最大应力为75.8 MPa，低于材料的许用应力；最大变形为0.18 mm。应力及变形云图分别如图9 及图10所示。

图9 轮毂应力云图

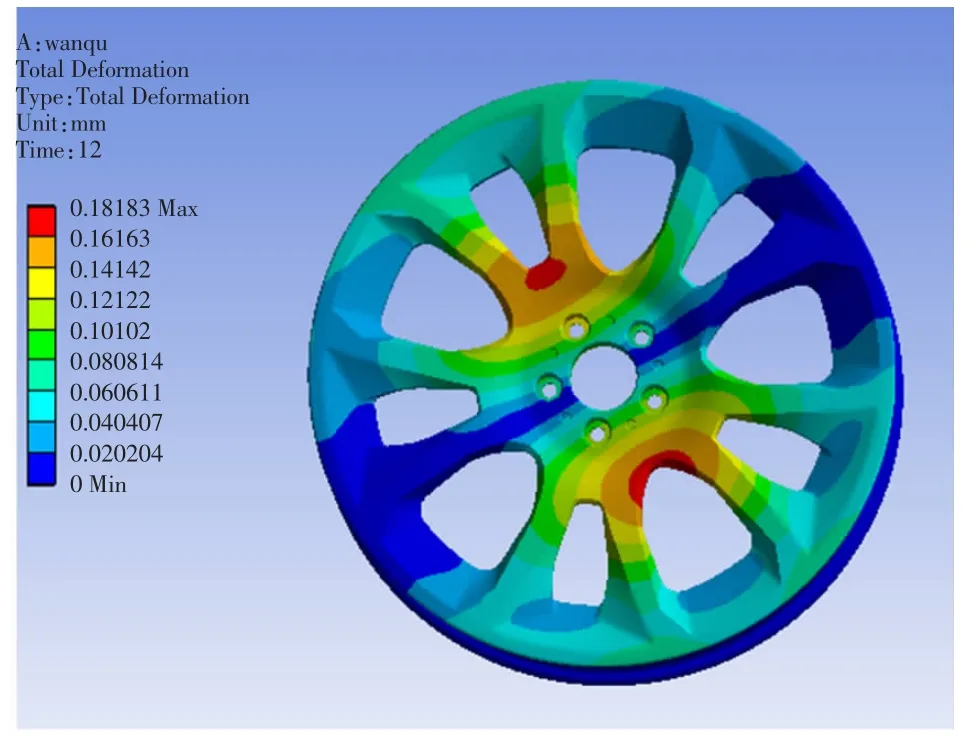
图10 轮毂变形云图

从图9 及图10 可知，最大应力及最大变形都出现在两轮辐之间。

至于螺栓预紧力对轮毂疲劳寿命的影响，研究表明，当轮辐螺栓孔是应力疲劳破坏区域时，不可以忽略螺栓预紧力的影响[11]。由上述有限元分析结果可知，轮辐螺栓孔处有应力集中区域。因此，该轮毂的螺栓预紧力不可忽略。

4 轮毂弯曲疲劳寿命预测

轮毂疲劳属于高周疲劳，因此采用名义应力法来预测轮毂的疲劳寿命较为准确。名义应力法估算轮毂的疲劳寿命一般是从材料的S-N 曲线出发，再考虑各种影响因素[12]。A356 材料的S-N 曲线如图11所示。

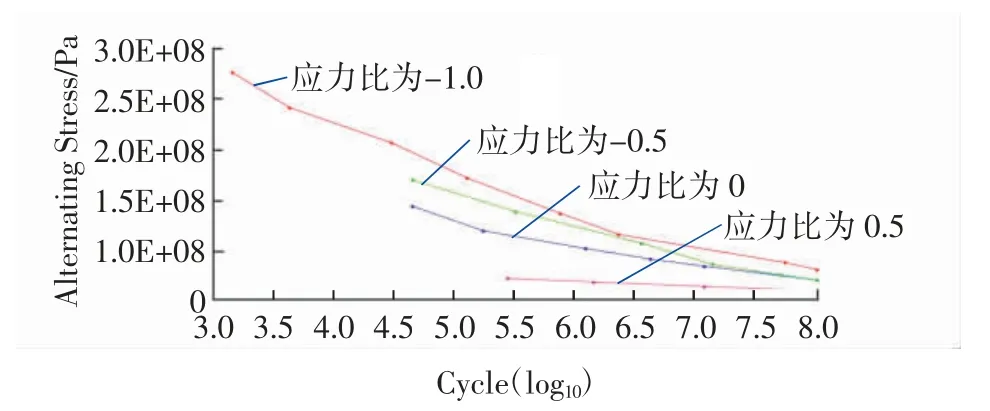
图11 A356 材料的S-N 曲线

在材料设置模块中，将轮毂材料设置为A356，螺栓和加载轴材料设置为结构钢。由于只考虑轮毂的疲劳寿命，因此在求解时，只对轮毂进行运算。

将ANSYS 静力分析结果导入Ncode Design Life的nCode SN TimeStep（Design Life）模块中，将12 步计算载荷作为一个循环进行加载，得到轮毂的疲劳寿命云图如图12 所示。

图12 轮毂疲劳寿命云图

从图12 可知，轮毂的疲劳寿命为2.8×107次，远大于设计所要求的最低循环次数。

5 结论

利用有限元模拟仿真方法，能够尽早发现轮毂结构设计中的缺陷，避免不必要的资源浪费。

本文根据GB/T 5334-2005《乘用车车轮性能要求和试验方法》对轮毂的弯曲疲劳寿命进行了试验研究，通过仿真分析，对铝合金轮毂的弯曲应力进行了运算，且考虑了螺栓预紧力对计算结果的影响。

利用静力学分析结果，通过Ncode Design Life 模块对轮毂的疲劳寿命进行了预测。仿真计算结果表明，轮辐为应力集中区域，最大应力为75.8 MPa，远远小于材料的许用应力；轮毂的疲劳寿命（最低循环次数）约为2.8×107次，高于强化系数为1.60 时的设计要求。

轮毂疲劳破坏区域集中在轮辐之间，该区域也是应力和变形最大的位置。因此，后续可对该部位进行优化以提高轮毂的使用寿命。

要强化研究型大学建设同国家战略目标、战略任务的对接，加强基础前沿探索和关键技术突破，努力构建中国特色、中国风格、中国气派的学科体系、学术体系、话语体系，为培养更多杰出人才作出贡献。

——习近平总书记在中国科学院第二十次院士大会、中国工程院第十五次院士大会、中国科协第十次全国代表大会上的讲话