基于BLUE的雷达/红外异步融合算法研究
盛 琥,汪海兵
(1.中国电子科技集团公司第三十八研究所,安徽合肥 230088;2.国防科技大学电子对抗学院,安徽合肥 230037)
0 引言
多传感器数据融合是当前研究的热点。以常见的雷达/红外数据融合为例,雷达探测距离远,单次观测就能定位目标,且具备全天候工作能力,但容易被反辐射武器打击;红外传感器不辐射信号,抗毁性强,测角精度高,但探测范围小,且无法测距,需要在其他传感器引导下发现目标。两种传感器组网,在中心统一调度下,对目标协同探测,信息融合,可实现优势互补、协同增效。由于两种传感器的观测模型不同,探测时间不同步,红外传感器数据更新率远高于雷达,因此该组网系统面临两个问题:一是如何基于不同传感器观测,估计目标状态,即非线性滤波问题;二是如何保证跟踪精度和实时性。
传统非线性方法包括扩展Kalman 滤波(Extended Kalman Filter,EKF)、粒子滤波[1](Particle Filter,PF)、容积Kalman 滤波[2](Cubature Kalman Filter,CKF)或无迹Kalman 滤波(Unscented Kalman Filter,UKF)、转换量测Kalman 滤波[3](Converted Measurement Kalman Filter,CMKF)等。上述方法中,EKF 计算量最小,但鲁棒性差;PF、UKF、CKF精度高,但计算量大,实用性差。CMKF 实现简单,且兼顾精度和计算量,因此应用较广。CMKF 中最具代表性的滤波方法是BLUE(Best Linear Unbiased Estimation),相比EKF,它的鲁棒性好;相比采样类滤波方法(CKF、UKF、PF),它的计算量小,因此在实用中受到重视,相关研究较多。其应用从常规目标跟踪,拓展到多普勒目标跟踪、只测角目标跟踪、机动目标跟踪等方面,在诸多场景得到应用[4-9]。基于以上分析,在雷达/红外组网系统中,应用基于BLUE的异步融合算法跟踪目标。
1 基于BLUE的雷达/红外组网系统
BLUE 滤波是CMKF 中的代表性算法。CMKF将非线性观测转换为直角坐标系内的伪线性表达,推导转换量测统计特性后,在Kalman 滤波架构下完成状态估计。目前已有嵌套CMKF、基于量测的CMKF、去相关CMKF 和BLUE 等多种算法,在多普勒目标跟踪、相控阵雷达目标跟踪中得到验证。BLUE 滤波相比其他方法,精度高、计算量小,没有Kalman滤波的诸多限制,因此受到关注。
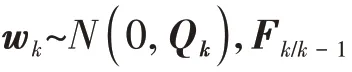
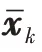

雷达/红外组网系统以指控中心位置为参考原点,估计目标状态;中心和传感器位置不同,各传感器的录取时刻和观测维度也不同,因此雷达和红外传感器需要采用不同的BLUE 滤波器,异步融合跟踪目标,具体步骤如下:
1)基于多帧雷达观测和目标运动特性,建立多个暂时航迹(可能的目标航迹)。
2)定期检查暂时航迹,判断其是否满足起始条件,满足条件转到步骤3,将暂时航迹转为稳定航迹,否则继续维护暂时航迹。
3)基于暂时航迹的历史观测,粗略估计目标初始状态,建立航迹。
4)如果雷达录取的点迹与航迹关联,采用改进BLUE 滤波器,更新该航迹;如果红外传感器录取的点迹与航迹关联,采用修正BLUE 滤波器,更新该航迹。
5)定期检查航迹,如果航迹连续多帧录取不到点迹,判断目标消失,删除该航迹。
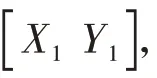
2 改进BLUE滤波算法
雷达观测为斜距rm,1和方位θm,1,观测与真值的关系为
当斜距和方位误差的乘积变大时,基于该模型的BLUE 滤波器性能变差。原因如下:将式(5)展开
方位估计θf,1是方位观测θm,1和方位预测θp,1的加权和,表达式如下:
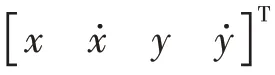
目标真实状态未知,因此方位预测的方差近似为

约束1:在垂直雷达视线方向(切向),方位观测误差要远大于方位预测误差;
约束2:在沿着雷达视线方向(径向),观测项误差要远大于预测项误差。
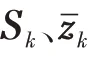
约束2的理由是:公式(8)中,雷达径向误差由观测项误差(与观测相关)和预测项误差(与预测相关)组成。BLUE 滤波器相关参数没有闭式解(是用位置预测近似得到),通过αk,1调节观测项误差在径向误差的比重,避免径向滤波发散。
约束1的数学表达式为
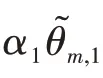
约束2的数学表达式推导如下:
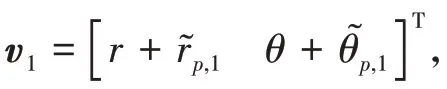
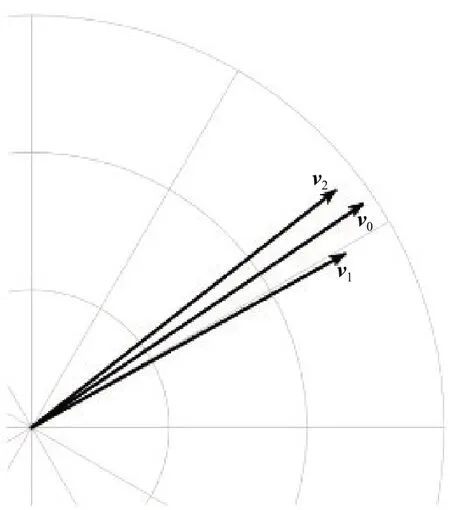
图1 观测向量、预测向量和真值向量示意图
近似时,假设方位预测误差远小于方位估计误差。͂的方差为

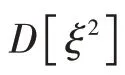
综合公式(12)和(17)两重约束,求解出公式(9)中αk,1表达式为
其中,
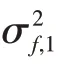
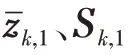
3 修正BLUE滤波算法
红外传感器观测θm,2与真值的关系为

得到rp,2后,构建k时刻转换量测zk,2,下标2 表示红外传感器的转换量测。
其中,
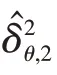
类似改进BLUE 滤波器,通过在红外传感器径向和切向上分别加以约束,可以求解加权系数αk,2。
约束1的数学表达式为
约束2的数学表达式为
αk,2的表达式如下:
其中,
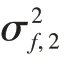
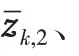
I是2阶单位阵,Λk,2定义如下:
其中,
基于以上滤波参数,对目标递归滤波,实现纯方位的BLUE跟踪。
4 仿真分析
下面仿真验证所提方法性能,场景1仿真参数如下:场景包括两部性能相同的雷达、一部红外传感器。雷达斜距误差σr,1=50 m,方位误差σθ,1=4°,两部雷达位于X轴上,相对Y轴对称放置,间距10 km。红外传感器位于坐标原点,方位误差为σθ,2=2°。目标从正北方向100 km 处向南飞行,速度(0,-50)m/s。飞行过程中,各轴的位置噪声独立无关,标准差0.1 m;速度噪声独立无关,标准差0.1 m/s。为模拟实际情况,传感器的观测时间不同步,而是等间隔交替探测目标,时间间隔T=1 s。蒙特卡洛仿真100 次,仿真时长200 s。将本文所提方法与经典BLUE 融合方法对比,二者区别是:当雷达探测到目标时,本文融合方法采用改进BLUE 滤波,经典融合方法使用文献[6]的BLUE 滤波;当红外传感器探测到目标时,本文融合方法采用修正BLUE 滤波,经典融合方法采用文献[17]的只测角BLUE 方法。两种融合方法都采取两点估计法来初始化目标状态,修正BLUE 和改进BLUE的放大倍数都设置为κ=6。对比的性能参数包括位置估计精度(RMSE)和归一化估计误差均方(ANEES),前者表征滤波精度,后者衡量滤波误差和实际误差的匹配程度,ANEES 为1 时,滤波一致性最好,估计置信度最高。仿真结果如图2所示。
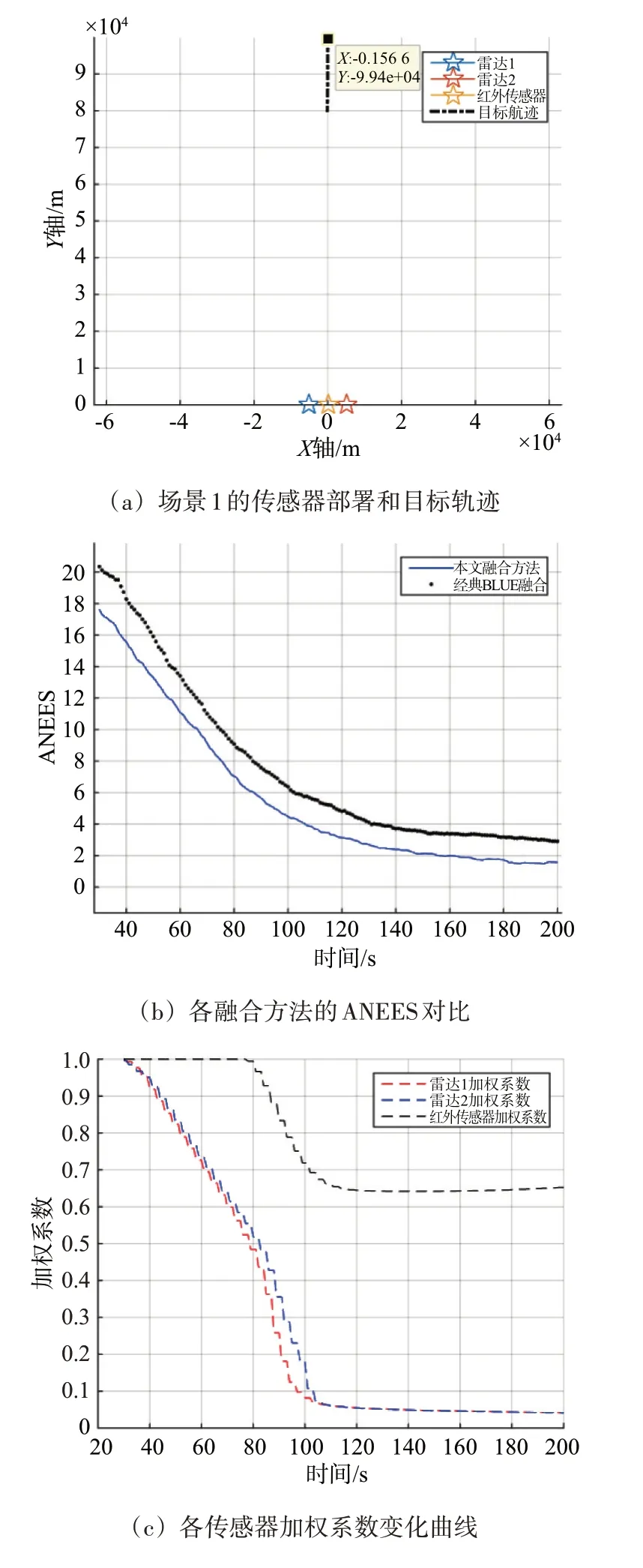

图2 场景1的跟踪性能对比
两种方法的初始跟踪性能接近,在跟踪稳定后(30 s 后),所提融合方法的ANEES 比经典BLUE融合更逼近1,也即滤波置信度更好,如图2(b)所示。由图2(c)可见,30 s 后,雷达加权系数小于1;80 s后,红外加权系数小于1,此时方位估计误差小于方位观测误差,所提融合方法的精度明显优于经典BLUE 融合,红外传感器的加权系数最终稳定在0.65,雷达加权系数稳定在0.05。所提方法位置融合精度(300 m)比经典BLUE 方法(800 m)提高2倍多,如图2(d)所示。
为评估所提方法在不同布局下的性能,场景2中,其他条件不变,将两部雷达间距由10 km 扩大到60 km。仿真结果如图3所示。
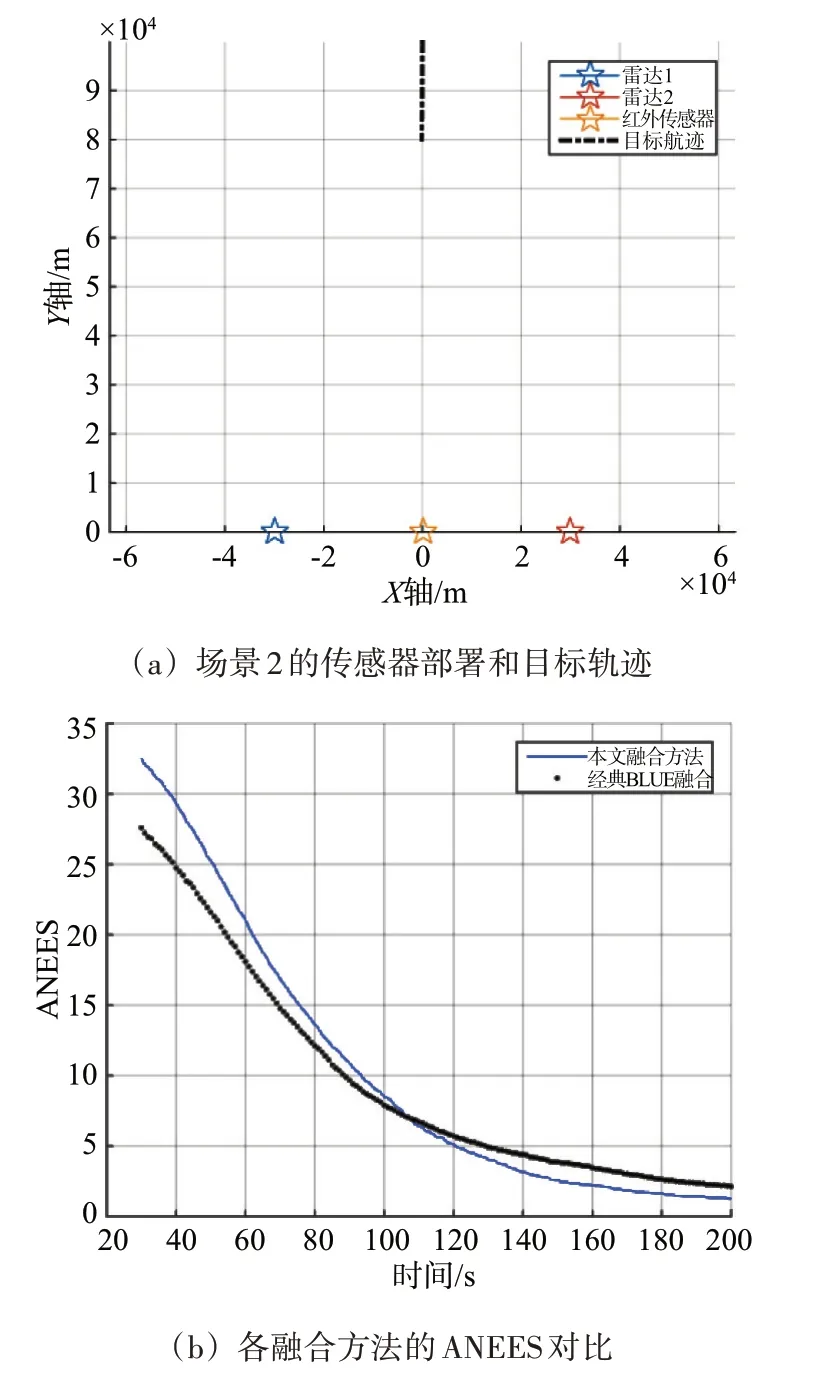
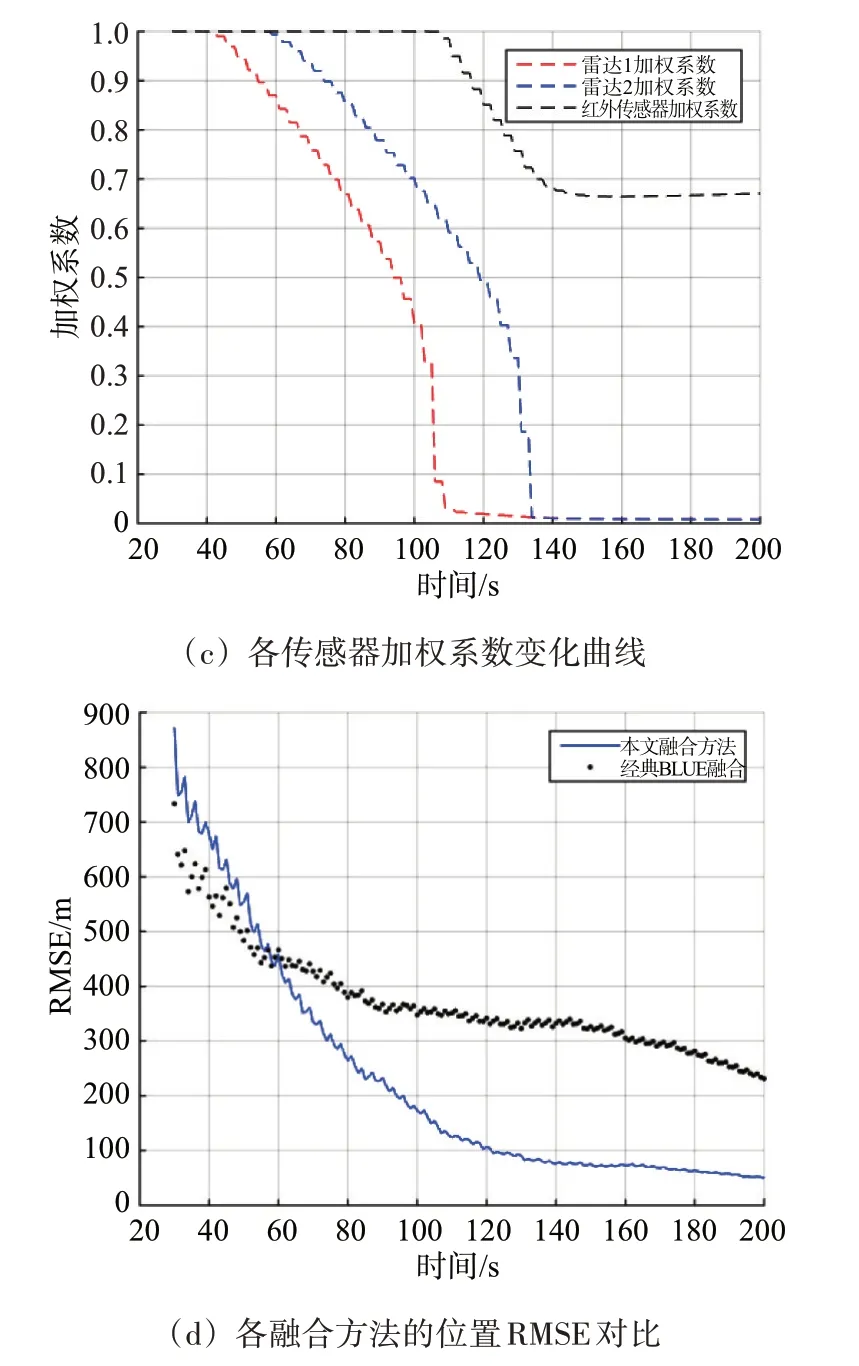
图3 场景2的跟踪性能对比
跟踪稳定后,两种方法的ANEES 变化情况类似,如图3(b)所示。在图3(c)中,红外传感器的加权系数约为0.65,雷达加权系数逼近0。几何布局的改善和方位估计精度的提高,使得所提方法的融合精度(50 m)比经典BLUE 方法(250 m)提高5倍,如图3(d)所示。
融合方法在两种仿真场景中的运行时间如表1所示。
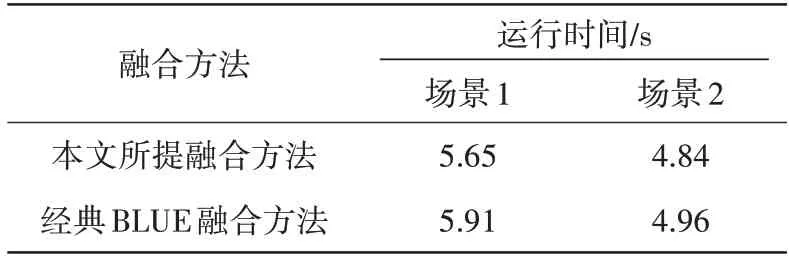
表1 各融合方法迭代运行时间对比(100次)
由表1结果可见,所提方法计算量略大于经典BLUE 方法,主要时间消耗在估计各传感器的加权系数上,相对于融合精度数量级的提升,这点时间开销可以承受。综上可见,基于BLUE的异步融合跟踪方法,可以用于雷达/红外传感器组网系统,在精度、置信度和计算量上具有优势,有较高的应用价值。
5 结束语
针对雷达/红外传感器组网,异步融合跟踪目标的问题,提出一种基于BLUE 的融合跟踪方法。在雷达跟踪目标时,采用改进的转换量测模型,提高估计精度;在红外传感器跟踪目标时,采用修正的转换量测模型,实现纯方位目标跟踪。理论分析和仿真实验证明:所提融合方法将估计精度提高2~5倍,实时性和鲁棒性都有所保证。其设计思想对其他多源信息融合的应用具有借鉴意义。

