计及负序控制策略的光伏逆变器故障特性分析

徐晓春，黄涛，谢华，赵青春

（南京南瑞继保电气有限公司，南京 211102）

0 引言

光伏发电通过全功率变流器并入电网，从电网看过去，其故障特性主要表现为逆变器的故障特性，与传统同步机存在较大差异。逆变器的故障特性由其采用的故障穿越控制策略决定，具有强可控性，研究清楚不同控制策略下逆变器的故障特性对以新能源为主体的新型电力系统的安全稳定运行具有重要意义。

光伏逆变器不存在恒定电势与阻抗串联的等值电路，对其故障特性的研究必须与详细的拓扑结构、控制回路、控制目标相结合。目前研究人员针对光伏逆变器的故障特性已开展了大量的研究工作。文献［1］通过理论与仿真结合，得出了光伏逆变器短路电流的基本组成、衰减速率以及幅值特征等与同步发电机存在较大差异；文献［2］仿真分析了交流电网故障、IGBT器件故障等多种情况下的逆变器输出短路电流特征，得出了短路电流不超过1.5倍额定电流的结论；文献［3］考虑PI控制器的限幅特性，研究了控制器分别工作在线性区、非线性区时逆变器短路电流暂态变化特征的差异；文献［4］推导了不依赖逆变器控制结构及参数的稳态短路电流计算公式；文献［5］在短路电流计算中计及了母线电压波动及卸荷电路的影响，并分析了PI控制器参数、电压跌落深度、负载水平等因素对光伏电源故障特性的影响；文献［6-7］研究了配电网中计及分布式电源的短路电流求解方法；文献［8-9］分别从光伏系统输出短路电流中含有衰减直流分量、负序分量出发，研究了逆变器输出电流中二次谐波、三次谐波的产生机理；文献［10-11］考虑锁相环的动态响应，给出了光伏逆变器更加准确的短路电流表达式。

但是上述文献在理论和仿真分析中，均没有考虑不同负序控制策略的影响，实际上光伏逆变器可以同时对正序电流和负序电流进行控制，文献［12］中详细研究了光伏逆变器可以采用的三种负序控制目标：抑制负序电流、抑制无功功率二倍频波动、抑制有功功率二倍频波动。在同步机系统中，故障期间负序网络中只存在故障点唯一的负序源，负序电压、电流的分布是比较明确的。如果逆变器对负序电流进行控制，则逆变器本身也可能成为一个负序输出源，将对逆变器的故障特性造成较大影响。目前有少量文献在逆变器故障特性的研究中考虑负序控制策略的影响，如文献［13］提到了三种不同的负序控制策略，但只选择了抑制负序电流这一种策略开展了研究；文献［14-15］针对不同的负序控制策略，研究了逆变型电源等效负序突变量阻抗相角特征对故障分量方向元件的影响，文中虽然推导了逆变型电源的短路电流表达式，但没有结合不同负序控制策略对不同故障类型下逆变器输出短路电流特性进行研究。

针对目前光伏逆变器故障特性的研究没有充分考虑不同负序控制策略的影响，本文首先推导逆变器短路电流的求解方法，然后重点考虑三种不同的负序控制策略，详细研究不对称故障情况下逆变器输出短路电流和等效负序阻抗在不同负序控制策略下的变化特性，并通过仿真进行验证。

1 逆变器短路电流推导

光伏逆变器一般采用功率外环和电流内环的双环控制架构，对输出电流具有很强的控制能力。当PI控制器设计合理时，逆变器输出电流能够快速地跟随上指令值［3］，可以忽略短暂的控制器暂态响应过程。

假设逆变器故障期间正向同步旋转坐标系下的正序电流d、q轴指令值为、，反向同步旋转坐标系下的负序电流d、q轴指令值为、。则逆变器输出稳态短路电流可表示为：

假设t=0时刻，d轴与a轴重合，对式（1）和式（2）分别进行正向、反向同步旋转坐标系下的Park反变换，然后两者相加可得到逆变器输出分相稳态短路电流：

式（3）可进一步整理为：

2 逆变器故障穿越控制策略

故障期间逆变器正、负序电流指令值的具体取值分别由其正、负序故障穿越控制策略决定。

2.1 正序穿越控制策略

当采用d轴电压定向控制时，分别控制d、q轴正序电流、可以实现逆变器输出有功功率、无功功率的独立解耦控制。

按照低电压穿越的要求，故障期间光伏逆变器应向电网输送无功功率支撑电压，无功电流指令值按照式（5）给定［16］。

式中：UT为并网点电压标幺值；IN为逆变器额定电流标幺值。

目前规范对故障发生至故障切除这段时间内的有功电流输出并没有要求，一般的做法是［9］：当UT＞0.9时，以有功电流输出优先，在限幅（本文取1.2IN）条件下，剩余裕度用于负序电流的输出；当UT≤0.9时，以无功电流输出优先，扣除无功电流输出及负序电流输出后，在电流限幅条件下如果还有额外的裕度则用来输出有功电流。

2.2 负序穿越控制策略

当系统处于不对称运行状态时，逆变器馈入电网的功率将发生振荡，导致输出电能质量大幅降低从而影响电网安全运行。当电网电压、电流不对称时，光伏逆变器输出功率可以表示为［15］：

式（6）中各项系数表达式如下：

式中：和分别为正向同步旋转坐标系下的正序d、q轴电网电压；和分别为反向同步旋转坐标系下的负序d、q轴电网电压。

国内外文献中已报道的负序控制目标主要有三种［12-15］：

1）目标Ⅰ：抑制电网负序电流，即i-=0。

2）目标Ⅱ：抑制逆变器的无功功率二倍频振荡，即Qc2=0、Qs2=0。

3）目标Ⅲ：抑制逆变器的有功功率二倍频振荡，即Pc2=0、Ps2=0。

采用d轴电压定向时，等于0，根据式（7）及式（1）、（2）可以得到各控制目标下负序电流指令值的统一表达形式如下：

式中：ρ=0、1、-1，分别对应控制目标Ⅰ、Ⅱ、Ⅲ。

3 逆变器故障特性分析

3.1 不对称故障电流特性分析

根据式（8），可进一步得到逆变器稳态输出正、负序短路电流之间满足关系：

由此推得：

由式（10）可知逆变器输出正、负序短路电流之间的相位关系取决于所采用的负序控制策略及负序故障电压。

1）单相接地故障

以A相接地故障为例，假设故障后电网A相电压跌至λ(0≤λ＜1)，则近似认为另外两相电压仍保持不变，即：

对式（11）进行反向同步旋转坐标系下的Park反变换，可得：

式中：ed和eq包含两部分，直流分量对应负序电压，两倍同步转速分量对应正序电压，即=(λ-1)/3、=0。

当采用负序控制目标Ⅰ时，i-=0，根据式（4）可知各相短路电流幅值相等均为|i+|。

当采用负序控制目标Ⅱ时，根据式（10）可得φ++φ-=180°，将其代入式（4），可得：

式中：φa、φb、φc的大小与|i+|、|i-|的相对大小有关。

可以看到，此时故障相A相短路电流幅值最小，B、C相短路电流幅值相等，这与传统同步机的故障特性存在明显差异。

当采用负序控制目标Ⅲ时，根据式（10）可得φ++φ-=0°，将其代入式（4），可得：

此时故障相A相短路电流幅值最大，B、C相短路电流幅值相等。

再结合式（3）可知，采用目标Ⅱ时，A相正序电流与负序电流相位差为180°，即两者反向；而采用目标Ⅲ时，A相正序电流与负序电流相位差为0°，两者同向。根据该特征可以画出图1所示的相量图，其中iφ(φ=a，b，c)为各相电流相量，为各相电流正序分量，为各相电流负序分量。从图1中看到，利用相量图可以很方便地得出与式（13）、（14）完全一致的结论。

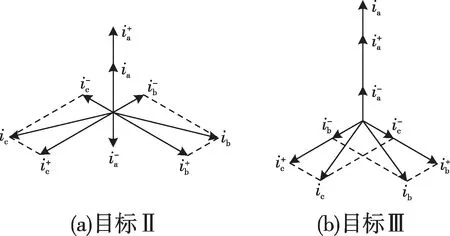
图1 不同控制策略下的相量图Fig.1 Vector graphics under different control strategies

其他单相接地故障可参照上述分析，结论与A相接地故障一致。

2）两相短路故障

以BC相间短路为例，根据边界条件及复合序网图可知，故障点A相电压仍为故障前电压，B、C相电压变为A相故障前电压的-0.5倍，有：

参照A相接地故障分析，有如下结论：当采用目标Ⅱ时，φ++φ-=0°，短路电流表达式与A相接地故障采用目标Ⅲ时一致；当采用目标Ⅲ时，φ++φ-=180°，与A相接地故障采用目标Ⅱ时的表达式一致。

两相短路接地故障可参考两相短路故障分析，同样可以得出类似结论。

综上分析，发生不对称故障时，在上述所设电压跌落前提下，不同负序控制策略下逆变器输出短路电流幅值特性如表1所示。

表1 不对称故障逆变器短路电流幅值特性Table 1 The characteristics of fault current magnitude of the inverter under an asymmetrical fault

由表1可以看出，当i-≠0时，逆变器输出稳态短路电流特性可以总结以下几点：

（1）采用负序控制目标Ⅰ时，各相短路电流幅值相等，短路电流中无负序分量。

（2）采用负序控制目标Ⅱ时，故障相短路电流幅值小于非故障相短路电流幅值。

（3）采用负序控制目标Ⅲ时，故障相短路电流幅值大于非故障相短路电流幅值。

（4）采用负序控制目标Ⅱ时的单相接地故障与采用负序控制目标Ⅲ时的另外两相短路（接地）故障特征相似。

（5）采用负序控制目标Ⅲ时的单相接地故障与采用负序控制目标Ⅱ时的另外两相短路（接地）故障特征相似。

需要说明的是，有些文献［3，10］中UT＜0.2时的无功电流指令值设定为限幅值，所有的电流裕度都将用来输出无功电流，不同负序控制目标下均不会有负序电流输出，逆变器三相短路电流始终对称，各相电流幅值相等。

逆变器输出短路电流特性的差异是由控制策略不同导致的，充分说明了逆变器输出短路电流的强受控特征，不同故障控制策略下，相同类型的故障呈现不同的故障特征，而不同类型的故障可能会呈现相同的故障特征，给传统故障选相、保护定值整定带来严峻的挑战。

3.2 等效负序阻抗特性分析

等效阻抗特性对继电保护原理分析非常重要，由于故障前不存在负序分量，等效负序阻抗可由故障后的负序电压和负序电流来计算［17］：

将式（9）代入，可以得到：

由式（17）可知，逆变器等效负序阻抗幅值等于正序电压与正序电流的幅值之比，阻抗相位与正序有功、无功电流及采用的负序控制策略有关。

假设故障后逆变器按照低电压穿越要求输出无功功率，即≥0，由于逆变型新能源一般都是送出有功功率，即≥0。在此前提下，如果逆变器采用负序控制目标Ⅰ，则其等效负序阻抗为无穷大，如果采用负序控制目标Ⅱ，则其等效负序阻抗角在-90°～-180°，如果采用负序控制目标Ⅲ，则其等效负序阻抗角在0°～90°。

可见，不同负序控制策略下，逆变器的等效负序阻抗特征差异显著，可能对传统利用负序分量的选相元件、方向元件造成影响。

4 仿真验证

利用电磁暂态仿真软件PSCAD/EMTDC搭建如图2所示的光伏逆变器并网仿真模型，1 MW光伏逆变器经两级升压后经并网线路接入110 kV无穷大电网。相关模型参数如下：35 kV变压器漏抗为0.065 pu、110 kV变压器漏抗为0.105 pu，变压器额定容量均为1.2 MW；并网线路正序阻抗为（0.19+j2.68） Ω、零序阻抗为（1.78+j8.6） Ω。

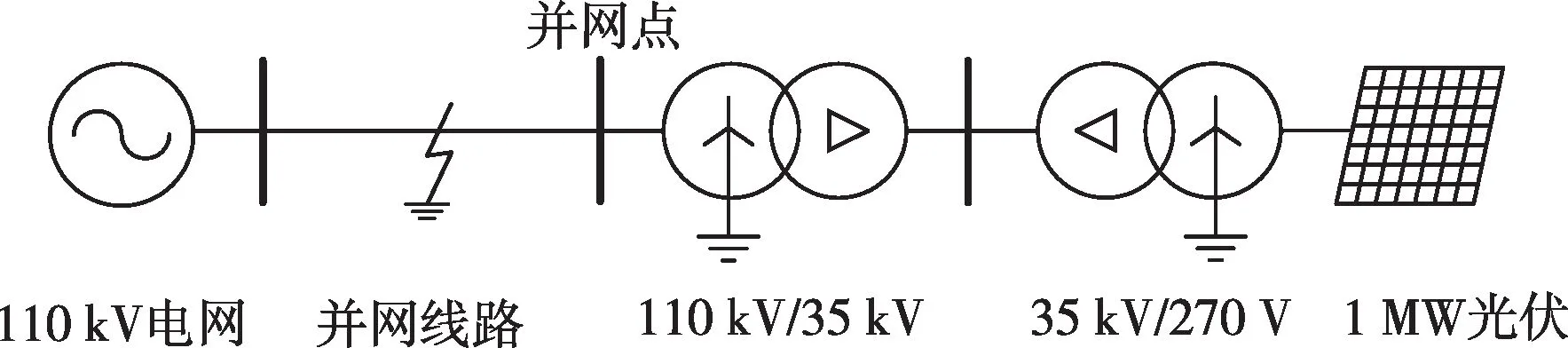
图2 仿真模型Fig.2 The simulation model

4.1 单相接地故障

故障前光伏逆变器输出0.5倍额定功率，0.4 s时在并网线路中点发生A相金属性接地故障。采用控制目标Ⅰ时的逆变器出口电压及不同控制目标下的逆变器输出电流波形如图3所示，电流波形中实线为仿真结果，虚线为用式（3）理论计算的结果。因故障后一个周波左右实际电流处在跟随指令值的动态过程中，理论值与仿真值存在稍许偏差，进入稳态后，两者基本重合，验证了稳态短路电流表达式的正确性。

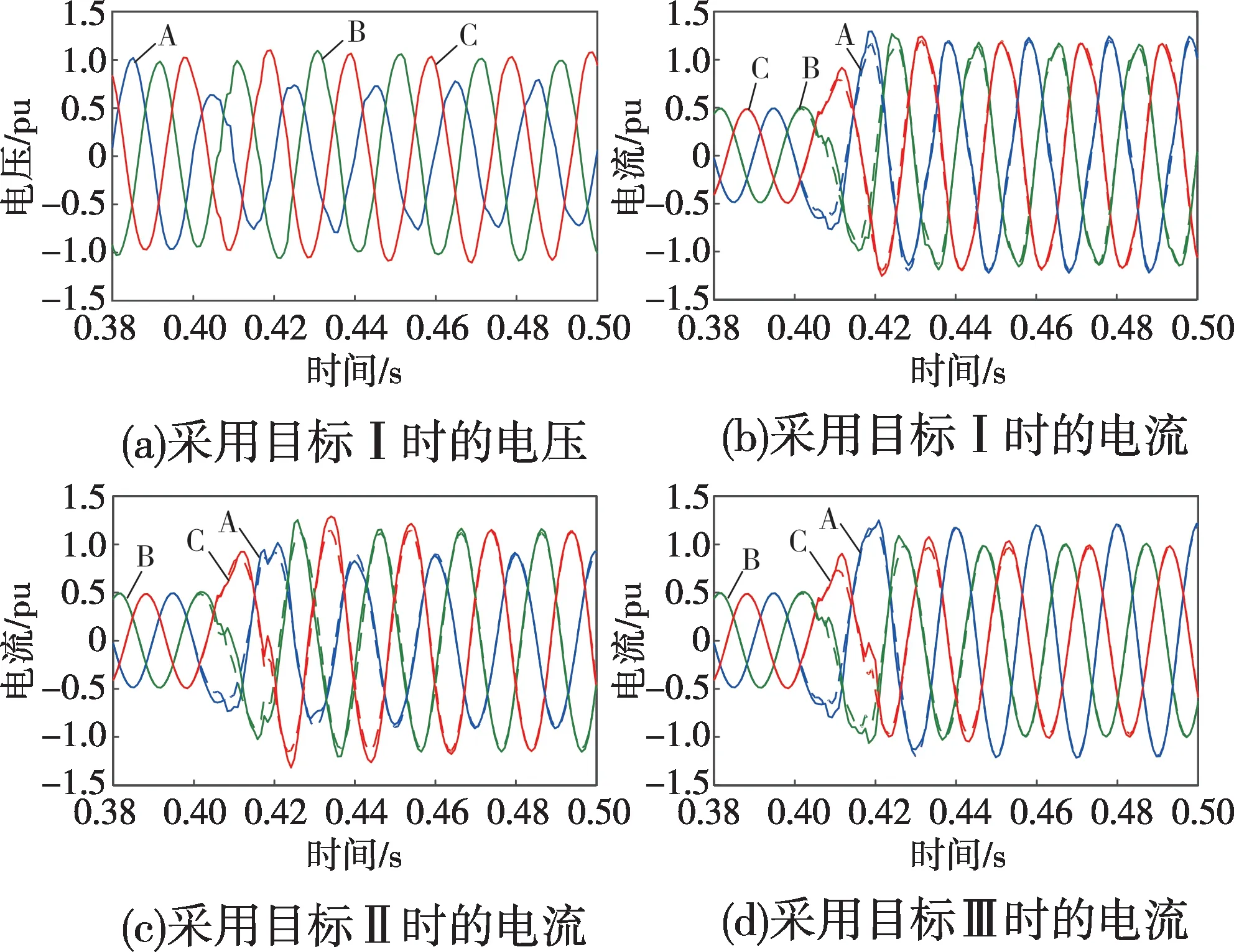
图3 A相接地故障逆变器输出电压、电流波形Fig.3 Output voltage and current waveforms of the inverter under phase A ground fault

从图3中看到，逆变器出口电压A相出现跌落，B、C两相电压基本保持不变，负序控制策略采用控制目标Ⅰ时，逆变器输出电流三相对称，基本无负序电流，采用目标Ⅱ时，故障相A相电流最小，采用目标Ⅲ时，故障相A相电流最大，与表1中的分析结果完全一致，直观地反映了不同负序控制策略对逆变器输出故障特性的影响。

不同控制目标下的逆变器等效负序阻抗幅值和相角特性如图4所示，其中实线为用逆变器出口三相电压、电流提取负序分量并采用全波傅氏算法计算相量求得的负序阻抗幅值和相角，虚线为用式（17）理论计算的结果。由于故障后电压、电流存在一个周波左右的暂态过程，且全波傅氏算法有一个周波的数据窗暂态，所以故障后前两个周波内理论值与仿真值存在一定的偏差，但是过渡到稳态后两者基本吻合。

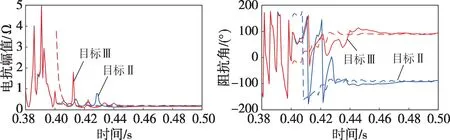
图4 A相接地故障逆变器等效负序阻抗特性Fig.4 Characteristics of equivalent negative sequence impedance of the inverter under phase A ground fault

由图4可知，采用控制目标Ⅱ和目标Ⅲ时，等效负序阻抗稳态幅值近似相等，但是相角差异较大，由于并网点电压跌落很大，逆变器有功电流指令值接近0，无功电流指令值为1.05 pu，可以看到采用目标Ⅱ时稳态相角在-90°左右，采用目标Ⅲ时稳态相角在90°左右，符合理论分析结果。

4.2 两相短路故障

故障前光伏逆变器输出0.5倍额定功率，0.4 s时在并网线路中点发生BC两相短路故障，采用控制目标Ⅱ时的逆变器出口电压及不同控制目标下的逆变器输出电流波形如图5所示。

图5 B、C两相短路故障逆变器输出电压、电流波形Fig.5 Output voltage and current waveforms of the inverter under short circuit faults of phase B and phase C

从图5中看到，逆变器出口A相电压稍有增大，B、C两相电压近似为A相电压的一半，相位相反。采用控制目标Ⅱ时，非故障相A相电流最大，采用目标Ⅲ时，故障相B、C相电流最大。从电流波形上可以看到，稳态时B、C两相短路采用目标Ⅱ时与A相接地故障采用目标Ⅲ时非常接近，而B、C两相短路采用目标Ⅲ时与A相接地故障采用目标Ⅱ时非常接近。说明不同故障类型下，采用不同负序控制策略可能得到相似的故障特性。

不同控制目标下的逆变器等效负序阻抗幅值和相角特性如图6所示，结果与A相接地故障相似，不再赘述。

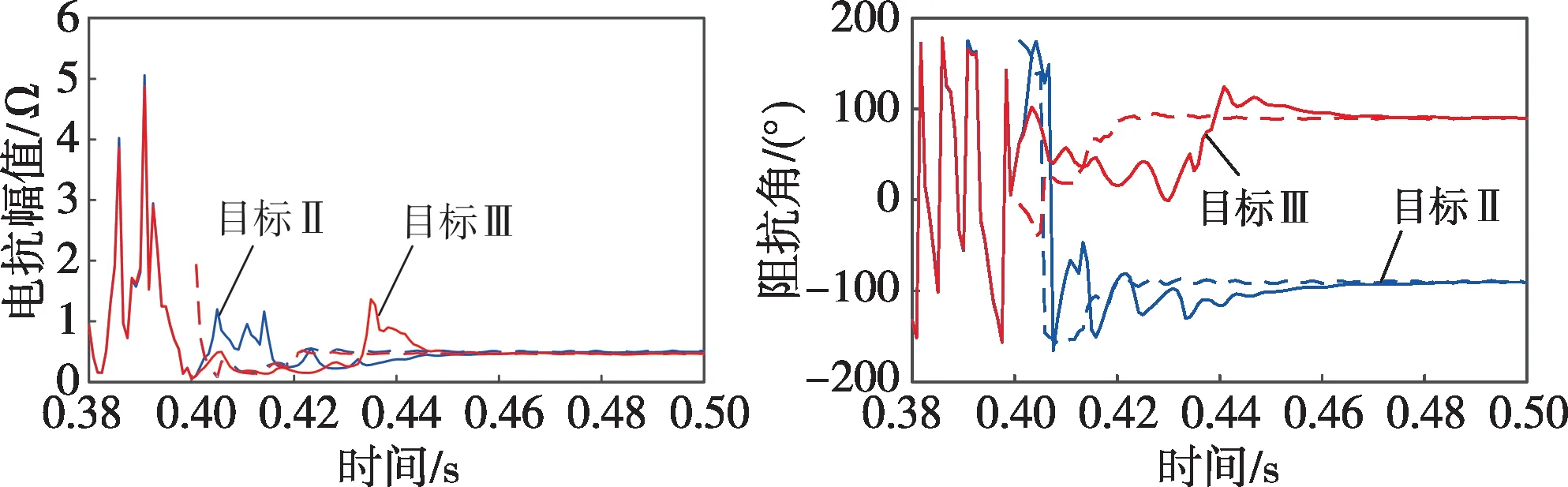
图6 B、C两相短路故障逆变器等效负序阻抗特Fig.6 Equivalent negative sequence impedance of the inverter under short circuit faults of phase B and phase C

5 结语

本文针对光伏逆变器，通过理论与仿真相结合，指出同一故障工况不同负序控制策略下，逆变器输出短路电流特性存在明显差异；而不同故障工况下，如果采用不同的负序控制策略，逆变器输出短路电流特性存在相似的情况。另外，不同的负序控制策略下，逆变器的等效负序阻抗的幅值和阻抗角同样存在明显的差异。因此，在新能源接入电网的故障特性及保护原理研究过程中需要充分考虑负序控制策略所带来的影响。