电力线中基于DFT 的信道估计算法改进

李冬娜，席回归，陈 忱，孙德乐

（兰州交通大学，甘肃 兰州 730070）

0 引 言

信道估计是正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）系统中的关键技术，通过接收端的信号采样和处理，对发送端与接收端的信道传输特性进行估计和建模。目前，OFDM 系统主要采用非盲信道估计，即先计算导频处的信道响应，后通过插值等方法估计完整的信道响应。在电力线通信中，因电网的分支结构和节点处阻抗不匹配，导致其信道的多径效应明显[1]。OFDM 技术可有效克服多径信道的影响，使得该技术广泛应用于电力线通信系统。前期学者在对信道估计问题的研究中，提出最小二乘（Least Squares，LS）算法、最小均方误差（Minimum Mean Square Error，MMSE）算法、离散傅里叶变换（Discrete Fourier Transform，DFT）算法等多种信道估计方法[2-4]。文献[5]通过在接收端对导频结构进行改进，采用压缩感知算法对限幅失真进行补偿来进行信道估计。文献[6]提出一种改进的加权范数最小化算法，以解决电力线脉冲噪声的问题。

电力线负载端频繁切换和线路老化发热，使得电力线信道具有衰减时变性和频率选择性[7]。对于脉冲噪声的干扰和阻抗不匹配引起的多径信道影响，传统的在加性高斯白噪声环境下的信道估计算法运用到电力线通信时效果较差。张华伟提出一种面向脉冲噪声环境的多径信道健壮估计方法；王毅对电力线信道相关性做了研究，对通信系统的性能具有重要意义；一些专家和学者在可编程逻辑控制器（Programmable Logic Controller，PLC）系统多径信道传输建模方面做大量研究，提出PLC 的多输入多输出（Multiple Input Multiple Output，MIMO）模型[8-10]。基于以上研究成果，针对电力线通信场景中多径效应带来的频率选择性衰落和噪声干扰等影响，提出一种基于DFT 改进的信道估计算法。

1 信道模型构建

载波信号在传输中会出现反射、透射等各种情况。信号从节点A到达节点C会出现多条不同路径，造成多径效应[11]。一旦信号到达传输媒体的边界，就会遭受反射的影响；透射为信号会穿透物体，同时改变方向和速度。多径信号的传播如图1 所示。

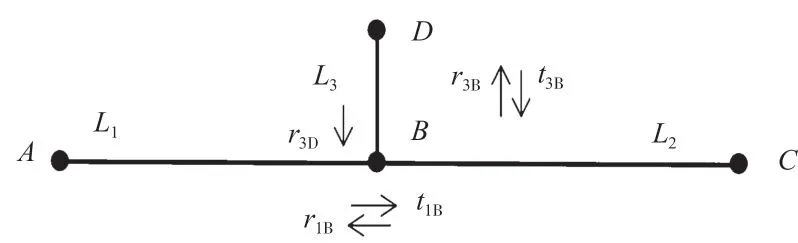
图1 多径信号传播示意

由图1 可知，该链路只有一个分支，由AB、BC、BD三段组成，长度分别为L1、L2、L3，阻抗分别为ZL1、ZL2、ZL3。假设A和C的阻抗与线路阻抗相互匹配，则可表示为ZA=ZL1和ZC=ZL2。其余反射点为B和D，反射因子记为r1B、r3D、r3B，透射因子记为t1B、t3B。在这些假设下，会引起无限多的传播路径，即A→B→C、A→B→D→B→C、A→B→D→B→D→B→C 等。

电力线信道同时可包含多种衰落特性，对于一些数字高速信号来说，低压电力线信道呈现为频率选择性衰落。M.Zimmermann 和K.Dostert 根据该假设提出一种经典的电力线多径信道模型[12]，其频率响应表示为

2 算法介绍及讨论

电力线多径信道中存在多个传播路径，造成传输信号的部分衰减，因此需要进行信道估计和均衡。基于DFT 改进算法的流程，如图3 所示。

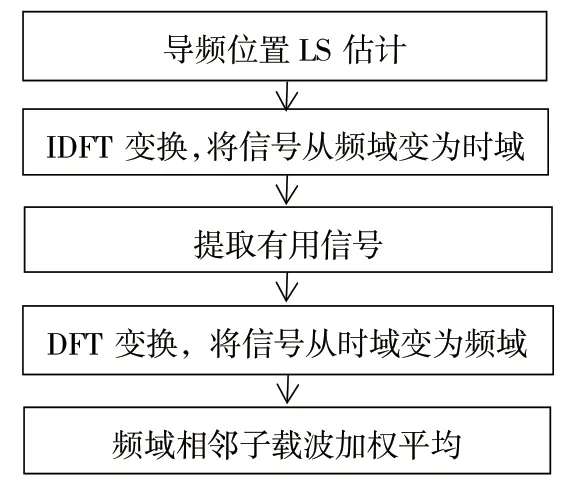
图3 改进DFT 算法流程

2.1 基于DFT 的信道估计算法

电力线信道为时变的频率选择性信道，因多径衰落对传输的OFDM 帧的影响，相邻子载波之间的信道存在相关性。

令Hi,L∈L×1，则。

Kp和Kd子载波对应的向量模型为

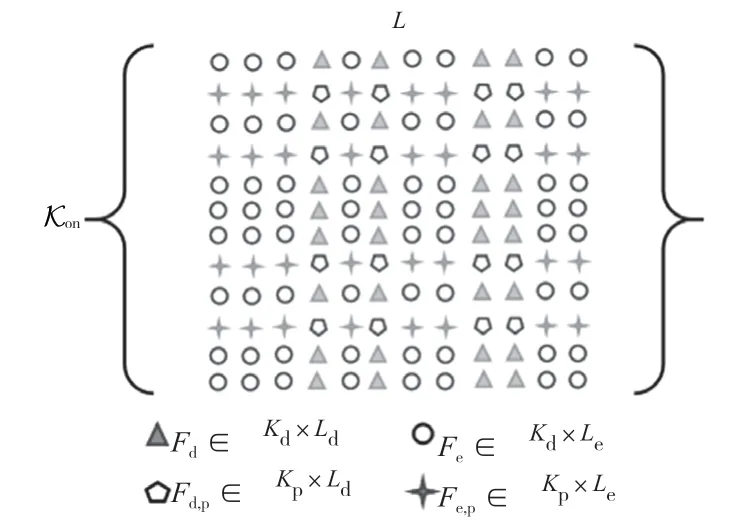
图4 截短DFT 矩阵

导频信号用于估计Hi,L，通过划分导频，可得

2.2 截断DFT 信道估计算法

电力线通信系统中的信道模型由15 个抽头组成。如文献[13]中所述，为减小多径效应带来的信号干扰，提出一种截断DFT 信道估计算法，目的是仅在主信道估计L 个抽头，使得Ld=Kp，其中主要抽头的索引为Ld，且Ld=|Ld|，可根据ρ[l,0]的信道脉冲响应幅度的最大值来选择。剩余小抽头由集合Le表示，Le=|Le|表示噪声，故Ld∪Le={0,…,L-1}。因此，令为对应于有效和次要信道抽头的向量，则导频信号可以改写为

类似地，数据子载波的信道增益可以表示为

先对其进行LS 估计，即

因此，PLC 信道条件下的截断DFT 信道估计算法可以表示为

因此，截断DFT 的MSE 可以表示为

2.3 考虑频率平均的FA-DFT 信道估计算法

电力线的信道频率响应随时间变化相对较慢，信道的相干时间的数量级比信道冲击响应的持续时间高出几倍[14]。

考虑电力线信道的慢时变性，一般采用块状导频，即将OFDM 每个子载波上估计的频率值直接用于信道估计。在现有研究中，子载波频率估计值之间的相关性往往被忽略，使信道估计的准确度下降。下面对相邻子载波之间的信道相关性进行分析[15,16]。

假设第m个子载波和第m+k个子载波的信道频率响应分别为Hm和Hm+k，且E{Hm}=E{Hm+k}=0，E{|Hm|2}=E{|Hm+k|2}[17]。

可知，信道频率值的相关系数为

由式（11）知，衰减系数hp、子载波间隔K及子载波数N影响子载波间的信道频域值，故有

由式（12）可以看出，此时的信号输出功率和噪声输出总功率分别为

因噪声与信号相互独立，则式（14）可改为

此时的加权处理增益为

一般情况下，K个相邻对称的子载波频域值加权且K为奇数时，则第n个子载波处的新的信道估计值为

这时的信号输出功率仍为Sout=Sin，噪声和总加权误差的输出功率为

式中：Δn+t,n=Hn+t-Hn。

此时，平均加权增益可以化简为

式中：p≠q且p≠0，q≠0。

当ρ≈1 时，式（19）进一步化简，即可获得信道平均的增益为

可见，子载波频域信道估计值的平均处理可减小冗余信息和噪声对信道估计的干扰。考虑到连续信道之间的频率相关性，令，其中是静态的，表示变化。同理，。因此，根据式（9）得到

FA-DFT 对应的信道表达式为

式中：γ为的权重。

这里整体误差项由为

该情况下，当i增加时，平均会降低噪声功率。在高信噪比时，误差受到非显著信道抽头误差c的影响，导致平均误差因的增大而增大。因此，平均增益在低信噪比下显著，在高信噪比下不显著，而在非常高的信噪比下更差。

3 仿真结果与分析

对信道估计算法进行仿真比较分析，具体仿真参数如表1 所示。

表1 仿真参数表

图5 给出不同算法在多径信道下的误码率曲线。可以明显看到：LS 算法的信道估计较简单易实现，但误码率较大且性能较差；MMSE 算法的信道估计受外界影响较小，性能好于其他算法，但该算法复杂度较高，没有获得广泛应用。相比于LS 算法，经典的DFT 算法在性能上更优，在此基础上提出的FA-DFT 改进算法进行相邻子载波间的加权平均，降低其信道估计的复杂度，提高信号传输的可靠性。

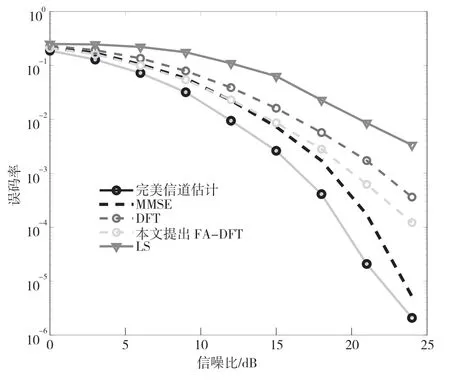
图5 多径信道下误码率曲线

图6 给出不同算法在多径信道下的均方误差曲线。当信噪比大于18 dB 时，所提的改进算法FA-DFT和其他算法的MSE 相差不大；当信噪比小于18 dB时，所提的改进算法FA-DFT 的MSE 比其他算法的MSE 都小。

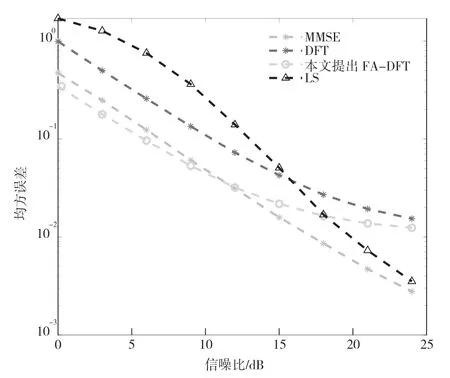
图6 多径信道下均方误差曲线

4 结 论

在DFT 算法的基础上，针对电力线通信中多径效应引起的噪声干扰和信号衰落问题，提出一种PLC系统下的改进DFT 信道估计算法——FA-DFT 算法。该算法对截断后的信道进行估计，对相邻子载波做加权平均，同时利用频率平均后的DFT 插值更新信道估计值，而不需要数据子载波和估计的信道统计数据。仿真结果表明，相比于其他算法，FA-DFT 算法在电力线多径信道下误码率最小、性能最优，可以有效提高信道估计的健壮性。