非显著特征数据挖掘中SOM聚类算法的优化
许丽娟,叶仕通
(广州华商学院 数据科学学院,广东 广州 511300)
1 引言
在数据泛滥的当下,对于兴趣推荐、故障检测、图像处理、传感数据融合等应用方面,数据挖掘需要面对越来越艰巨的挑战[1]。对于一些传统应用需求,其任务就是对信息流进行主特征的识别,比较流行的处理手段通常包括特征提取、关联规则,以及一些结合生物智能的聚类等[2]。数据特征深入研究可以分为显著与非显著,目前这些算法的提出主要针对显著特征的检测识别,很少有专门针对非显著特征的算法,对于当前日益增长的复杂应用场景,已经很难满足实际应用需求。比如存在稀疏甚至非规则数据,或者邻域范围内存在离群现象的场景,会因噪声数据引入很多伪点,影响数据挖掘精度的同时,也增加了挖掘耗时,使算法性能整体被拉低[3,4]。
为了增强对信息的识别性能,一些学者已经关注到非显著特征的数据处理领域。文献[5]为了降低视频图像检测的精度偏差,先将原始数据采取滤波操作,得到初步特征域,再根据SUSAN搜索其中的角点,推导灰度差异,最终完成特征识别。由于该算法是基于视频图像设计的,尽管在实验中表现出优秀的鲁棒性,可是很难将其迁移到数据的检索和挖掘应用中。文献[6]先对数据采取分解,再把各分解属性做匹配计算,从而得到特征分类。经过在云计算数据库上的仿真测试,验证了该算法拥有良好的实时性,而在精度方面还有欠缺。文献[7]针对多噪声干扰引入滤波操作,为防止滤波发散设计了协方差比较,并采用模糊推理进行结果纠正。基于云计算平台的数据实验,验证了该算法对于传感数据融合的可靠性,但是对于子域内的一些特征挖掘效果不够理想。
由于数据挖掘的目标就是确定数据发展倾向,这与聚类的目标不谋而合,而SOM[8]因其在文本处理上表现出良好的学习性,本文提出SOM与聚类算法结合,完成对非显著特征数据的挖掘。在传统的一些SOM模型设计中,由于神经元规模过于庞大,使得本应归为一类的特征却未被支配到同一个神经元[9],因此对特征分类结果产生严重干扰。而当前对SOM的优化模型,大部分是对数据特征的逼近效果做改善处理,从而也带来了算法过拟合的诟病。本文基于时频分析和宽平稳过滤,来得到非显著特征。并基于修正链接权重的SOM模型进行特征训练,最终改善聚类的敏感性和适应性,增强对非显著特征的挖掘效果。
2 非显著特征挖掘
假定原始数据为U={u1,u2,…,ue},其中任意元素都是矢量,将非显著特征基于频域进行分析,得到频域方程如下
ue=Uef+δeL(t)
(1)
f代表特征传函;δe代表估计偏差;L(t)代表负载平衡模型,公式如下
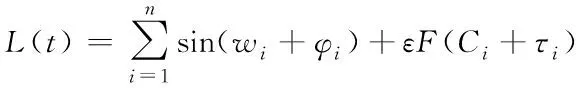
(2)
wi代表相位;φi代表融合程度;ε代表修正程度;F(Ci+τi)是拟合操作。通过宽平稳特征,对特征采取过滤,公式如下

(3)

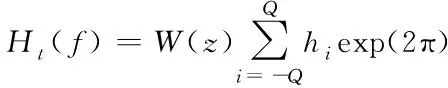
(4)
hi表示发送载波。通过时频域的分析,可以完成非显著特征的提取,以及拟合处理。在采用学习网络对特征数据进行挖掘训练的过程中,应该保证符合如下限定

(5)
ri(k)是序号为i的非显著特征。训练的期望公式如下

(6)
η是常系数;δ是训练偏差。
此外,在训练过程中,由于离群因子对特征分类的具有明显的影响作用,于是这里针对非显著特征将其进行重新定义。假定任意数据r,它的相似k近邻记作SK(r)={r1,r2,…,rl+1},l表示r邻域范围内的对象数量,且邻域范围内对象包含r自身。根据r的邻域情况,将离群因子公式表示如下

(7)
其中,Q(r)表示r的邻域对象集合;dis(i)表示对象i的相似k距离。
3 SOM网络聚类模型
SOM作为神经元聚类,具有无监督学习优势。利用输入与神经元的比较,决定网络输出结果,且每次比较输出具有唯一性。所有输出根据加权值向输入靠拢,直至全部近似特征完成汇集为止。
图1描述了SOM的神经元模型。其中,input为特征向量,表示为I={im|m=1,…,k},m代表I的维度。经过比较筛选,获胜的神经元来到output层,对于任意获胜神经元n,加权值可以描述成Wn={ωmn|m=1,…,k;n=1,…,d},d代表output神经元数量。由input层的I与加权值,就可以得到如下的欧氏距离求解公式
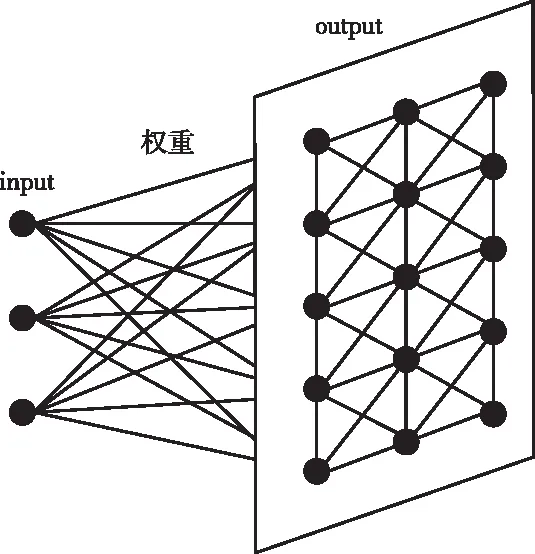
图1 SOM网络模型

(8)
对于SOM学习网络,ωmn代表的含义为input层第m维向量和output层第n个筛选结果的链接权重。利用式(1),求解出最小dn(I)所对应的神经元。并以此神经元作为基准,在一定范围内对其加权值进行调节,从而保证和input层向量的自适应近似性。在SOM模型中,output层筛选出的神经元数量对于最终结果有着重要影响。如果output层的输出不足,则会使得分类不够细致;而如果output层的输出超量,则会使得网络产生很多无效节点。基于此,本文提出如下方式计算output层输出数量
d=nc+as0+b
(9)
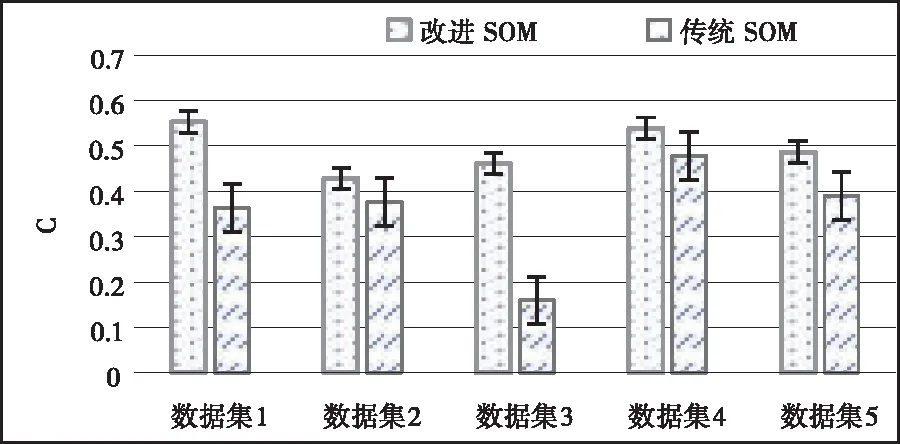
nc代表聚类的个数;s0代表原始节点规模;a代表s0的影响因子;0 根据加权值的变化范围,SOM链接加权的更新公式为 ω′mn=N(t)·Rm(t)·(in-ωmn) (10) t代表学习进行至第t轮;N(t)代表学习率;Rm(t)代表加权值的搜索空间。在学习轮次增加过程中,由于输出逐渐趋于稳定,学习率也将逐渐降低。 通过以上自组织投影,SOM便能够实现input层样本的训练工作,在ωmn作用下使网络输出结果稳定接近输入I。再经过属性计算,就可以达到聚类结果至output层神经元的投影计算。虽然此时的SOM中,任意样本仅存在唯一的活动神经元,可以有效保证ωmn和I具有相同的分布状态,但是为了能够令ωmn和所属类具有更好的拟合效果,需要对ωmn的调节方式采取进一步完善。引入加权调节修正因子,于是链接加权的更新过程描述为 ω′mn=N(t)·Rm(t)·(in-ωmn)+N(t)·C(t) (11) C(t)是修正向量,表示为 C(t)={c1(t),c2(t),…,ck(t)} (12) 其中,ck(t)是目标函数,它的数量由输入向量的维度决定,函数具体形式为 (13) (14) 假定α与β满足高斯分布,则根据maxck(t)能够推导出如下关系 (15) Trace(·)表示对矩阵对角线进行累加计算;T表示Hessen矩阵。 通过C(t)纠正神经元之间的链接加权。由于ck(t)值和逼近程度成反比关系,因此,纠正过程就是寻求最小ck(t)过程。基于此,再根据正则因子对纠正的过程进行约束,从而限定ck(t)值,防止出现过拟合现象。 仿真前,通过电商平台搜集五类商品数据,将其映射成固定格式作为原始数据集,具体的实例与特征情况如表1中所描述。基于Python的gensim对数据采取向量构造,并实现SOM训练模型。训练过程中邻域半径是0.3,学习率是0.5,原始节点规模的影响因子a=1,最大迭代数量是1000此。 表1 初始数据集 图2是对数据1进行非显著特征聚类的结果,实验设定了5个非显著特征的类别。 图2 聚类结果 通过可视化结果可以看出,经过SOM训练后,确实出现了5个非显著特征的聚集簇,其它类型数据分散周围。 为了定量分析所提SOM优化算法的聚类性能,引入如下评价指标: 1)准确率,用于衡量被正确分类的样本占全部样本的比例,计算公式为 (16) Ncorrect代表被正确分类的样本数量;Ntotal代表全部样本数量。ACC值越大,意味着聚类算法的识别效果越好。 2)凝聚程度,用于衡量分类中样本之间的耦合程度,计算公式为 (17) n代表聚类的数量;Ni代表聚类i中样本数量;i代表聚类i中错误分类的样本数量;ai代表与聚类i产生关联的神经元数量。C值越大,意味着样本聚类的越为紧凑,内敛效果越好。 将本文提出的改进SOM聚类与传统SOM算法做性能比较,针对5个数据集,分别得到两种聚类算法的ACC值与C值,结果比较如图3和图4。 图3 准确率对比 图4 凝聚程度对比 由ACC的结果可得,改进SOM算法对于不同数据集的聚类处理差异相对较小,平均准确率达到97.44%。而传统SOM聚类对于不同数据集的处理敏感度很高,聚类准确度波动明显,平均准确率仅为92.87%。这表明改进SOM算法具有良好的适应性与鲁棒性。 从凝聚程度对比可得,在5中数据集测试中,改进SOM算法的最高凝聚程度达到0.553,平均凝聚程度为0.493。而传统SOM的最高凝聚程度为0.478,平均凝聚程度仅为0.353。这表明改进SOM算法的输出结果具有更好的低耦合高内敛效果。 聚类效果的改善,主要得益于链接权重计算时采用了修正因子,并采取贝叶斯对链接权重进行更新计算,保证了算法对不同维度不同类型数据的适应性和识别率。 为了衡量数据挖掘性能,对算法的准确性和执行时间进行仿真测试。采用文献[5]、文献[6]和文献[7]中算法,以及传统SOM算法作为比较,引入均方根误差和执行时间指标。其中,均方根误差计算方式如下 (18) RMSE值越小,意味着数据挖掘的准确性越高。 关于RMSE的结果对比如图5所示。通过不同算法的比较可得,SOM优化算法的RMSE指标较文献[5]、文献[6]、文献[7],以及传统SOM算法分别降低了0.307、0.125、0.062、0.640,对非显著特征数据挖掘精度得到明显提升。 图5 RMSE结果对比 关于各算法的执行时间对比如图6所示。通过比较可得,SOM优化算法的执行时间虽然不是最短的,但是已经能够满足当前数据规模下的挖掘需求,且同时保证良好可靠的挖掘准确性。 图6 执行时间对比 本文针对非显著特征数据挖掘存在的问题,采取时频分析结合滤波算法的方式,降低稀疏与噪声影响。同时考虑到特征训练网络的非监督性,引入SOM,并对其output输出和链接权重的更新方式分别进行了优化设计。通过多个数据集上的可视化结果与数值结果,证明了改进SOM具有很高的准确度和凝聚程度;在非特征数据挖掘时,在较小的执行时间内,能够保证较低的挖掘误差,各项数据充分表明所提算法在非特征数据挖掘方面的性能优势。

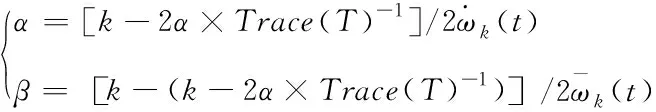
4 仿真与结果分析
4.1 仿真数据集

4.2 聚类效果仿真

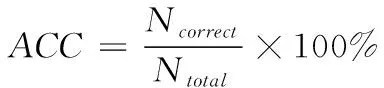


4.3 数据挖掘效果仿真
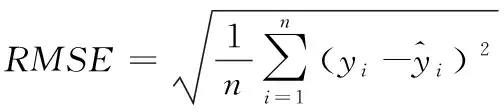


5 结束语

