液滴撞击非疏水性运动壁面的分析与研究

夏悦然,刘彩霞,张 静,田颍哲

(合肥工业大学物理学院,安徽 合肥 230009)

1 引言

液滴与固体表面撞击是常见自然现象,普遍存在于工业和农业等领域[1-5],如农业中喷涂杀虫剂,要求液滴在植物叶表面高附着率以提高杀虫效果;工业喷涂工艺,要求液滴在喷涂表面铺展均匀以提升喷涂质量;电力传输中,要求液滴在高压电线表面上的疏水性好以免结冰。因此液滴撞击表面产生损伤或粘滞于其上[6,7]的铺展、收缩、反弹等动力学行为引起了广大研究学者的关注。

近些年,研究人员对液滴撞击壁面的液滴铺展、反弹等过程进行了大量研究,Cheng M,Mohasan M和Pasandideh-Fard M等[8-10]学者利用数值模拟液滴撞击壁面演化过程,并对影响液滴演化过程的液滴下落速度、撞击角度、最大铺展直径等参数进行了研究,张振宇等[11]探讨了“气膜”对液滴最大铺展直径的影响;上述研究主要关注液滴撞击静止壁面的特性,而实际上在农业、工业和医疗领域中,液滴撞击移动壁面更为广泛。杨宝海等[12]利用高速摄像机研究了直径为2.58mm的液滴在不同速度下撞击静态接触角为156°超疏水壁面后的运动特性,结果表明液滴撞击壁面的速度对液滴的前进角、后退角,三相接触线的速度以及液滴反弹后的空中运动特性都有较大的影响;Palacios等[13]对液滴在不同的雷诺数与韦伯数下撞击干燥固体表面进行了实验研究,指出在低雷诺数下,液滴铺展的薄膜在薄气垫上移动。Chen等[14]人通过实验探究了液滴撞击旋转的圆柱形四氟乙烯表面时导致的部分反弹、沉积和分裂沉积,发现碰撞结果取决于法线韦伯数和切线韦伯数;Almohammadi等[15,16]研究了不同黏度液滴撞击疏水程度不同的表面时,液滴铺展与回缩的情况。Castrejón-Pita等[17]利用液滴撞击移动流体,研究了液滴与流动液面的融合、反弹等现象。

综上所述,已有研究工作主要集中在液滴与壁面接触后的演化过程上,对液滴与壁面的接触角、最大铺展直径及破裂后产生的子液滴研究较多;部分学者[18-20]关注到“空气薄膜”,其中Kim认为液滴反弹条件为空气薄膜存在,液滴具有足够的动能弹起,但其研究中仅提到空气薄膜会在液滴下落速度较小时存在,并没有对移动壁面能够产生“空气薄膜”的条件与液滴弹起机理进行探究。

为了探究液滴撞击移动壁面时“空气薄膜”形成与液滴弹起的条件,本文根据液滴与移动疏水表面撞击过程的物理现象及受力关系,推导空气薄膜形成的临界气场速度,基于质量守恒定律和动量守恒定律,利用数值仿真计算探究铺展液滴与固体表面之间空气薄膜的形成过程,分析壁面移速、液滴下落高度、液滴与壁所成角度对空气薄膜形成的影响,对液滴形变产生夹角进行详细分析,阐明液滴疏水性增加并弹起的机理。

2 理论分析

2.1 液滴撞击移动壁面的演化过程分析

液滴在不同条件撞击固体表面时,会发生破裂、粘滞、反弹等现象。Wu等人[21]研究了液滴破裂条件,即液体的韦伯数与雷诺数满足不等式 (1) 时发生破裂,分裂出子液滴:

(1)

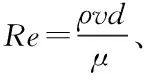
液滴撞击疏水表面时,动能转换为表面能并发生形变与铺展,在表面张力作用下铺展液滴迅速回缩,表面能转换为液滴动能,实现弹起[22]。一般情况,液滴撞击静止非疏水表面时,能量因黏性作用被耗散,黏滞在固体表面无法弹起。但液滴撞击非疏水性运动表面时,两者间形成空气薄膜减小液滴动能损耗,能够实现反弹。

根据液滴与移动疏水表面撞击过程的物理现象及受力关系,建立如图1液滴撞击移动壁面演化过程示意图。运动壁面带动表面附近空气作同方向运动,形成稳定流场u0,如图1 (a)。液滴下端液膜因接触流场发生形变,当固体表面以速度A向右运动时,流场对液滴产生向右剪切力,液滴非对称铺展,液滴下部空间空气向左右两边排出,如图1 (b) 所示。当液滴下降到运动壁面附近,由于空气流场的作用,液滴左下侧的空气阻力较大,液膜右下侧先与壁面接触,液滴变形为扁平椭圆液膜,液膜与壁面形成夹角。由于液滴左侧稳定流场阻止空气排出,使液滴与移动壁面之间形成空气薄膜,液膜与壁面间空气不再从右端流出,从而对液滴产生升力,如图1 (c)。受挤压影响,空气薄膜压强增加且其压强明显大于上方空气,为液滴提供向上作用力,在表面张力作用下液滴表面能转换为动能,实现液滴弹起,如图1 (d)。

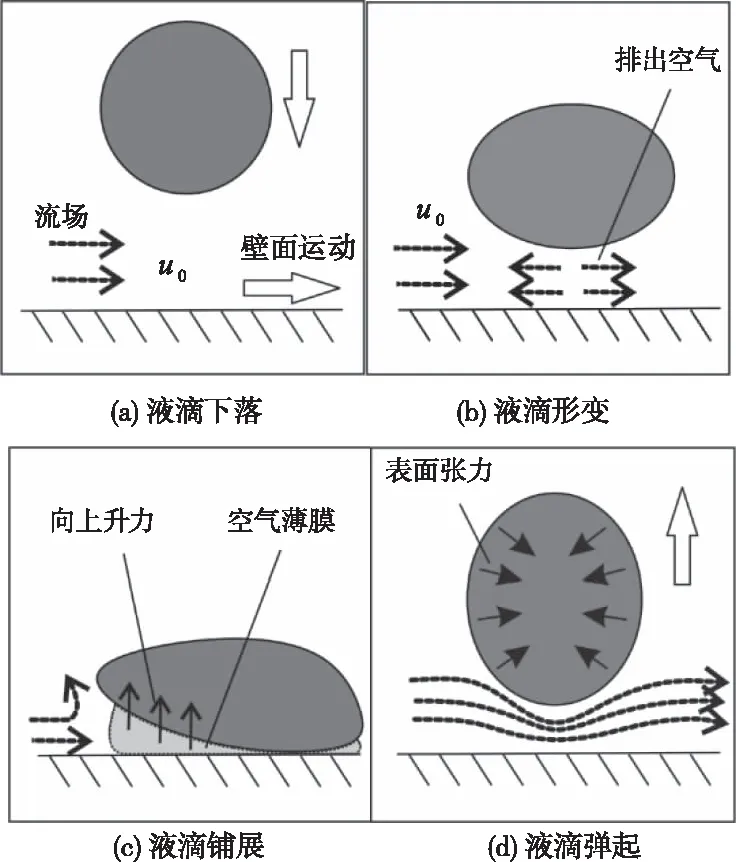
图1 液滴撞击向右移动壁面演化过程

2.2 基于流场理论的空气薄膜形成计算

由于液滴在下落和撞击过程中,沿壁面运动方向有铺展现象,在垂直于壁面运动方向上是中心对称的,因此在中心对称面上建立图2所示的坐标系xOz,X轴为壁面,其正方向与流场方向相同向右。液滴下端弧面与移动平面夹角为θ,为了方便计算,液滴下端弧面视为平面 (后续仿真结果显示可近似为平面),R为液滴半径。

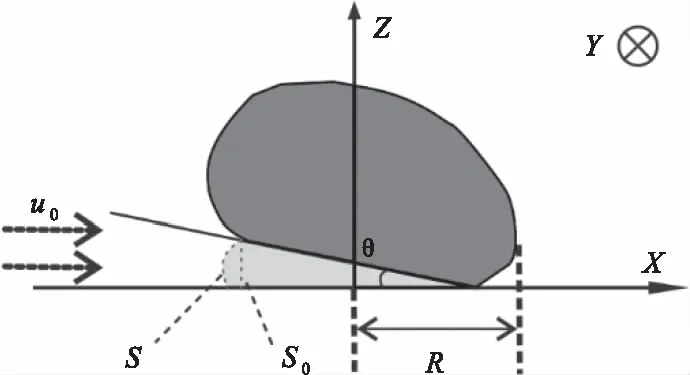
图2 液滴撞击平面坐标系

在空气流速较小 (远小于100 m/s) 且为室温时,可忽略空气密度的变化,视为不可压缩气体[23]。对空气薄膜区域应用质量守恒定律,得到如下表达式:

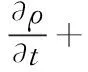
(2)

液滴下落撞击移动壁面产生空气薄膜,对空气薄膜所成的封闭区域进行分析,流体质量增加量等于该区域内流进和流出流量之差,得积分式

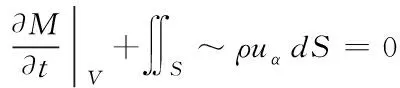
(3)

其中:M为空气薄膜质量,V为空气薄膜体积,S为空气薄膜与薄膜外空气接壤面积,空气流出量即为空气薄膜体积变化量,可得空气流出量为:

(4)

S=∮L(Rtanθ-xtanθ)dl=4πRtanθ,uα为无流场时,流出空气薄膜单位体积气体流量,表示为:

(5)

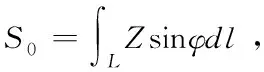
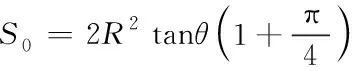
(6)

则封闭区域流体质量增加量为uβS0,uβ为空气流场总速度,利用动量守恒定律得:

-uαρS0uαdt+u0ρS0u0dt=uβρS0(uα+u0)dt

(7)

等式左侧第一项为S0投影至YoZ平面的流出空气动量,质量为ρS0uαdt,ρ为空气密度;第二项为流入空气动量;等式右侧为空气总动量。求解 (7) 得

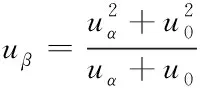
(8)

当流入空气体积大于或等于流出体积,即uβS0≥uα(S-S0)时,形成空气薄膜,否则液滴黏滞在移动表面。形成空气薄膜气流速度u0与下落高度h关系为:

(9)

其中:θ为壁面与液膜下端弧面夹角,与流场u0大小、液滴的黏度和表面张力系数有关,和孙志成提出的“铺展因子”概念[24,25]相似,用以描述液滴在撞击移动表面时铺展程度,即液滴受移动表面影响的形变程度,而该物理量无法通过理论推导出。控制液滴在1～10 cm高度下落,通过建模仿真研究液膜与移动壁面夹角θ。

3 数值模拟仿真研究

3.1 几何模型建立

基于前面的理论分析,本节探讨液滴在1～10 cm高度下落,通过数值模拟分析方法研究液膜与移动壁面撞击的夹角θ变形。建立液滴/空气的二维模型,液滴半径为0.5 mm,液滴中心坐标为 (-1,0) mm,液滴周围建立7mm×3 mm长方体区域代表空气,用COMSOL仿真软件对液滴及其周围空气进行网格剖分。为保证研究小尺度流体结果精确性,并减少计算机运算量、提高研究效率,对模型进行区域划分,如图3 (a)。蓝色区域内采用极细化网格,灰色区域因不涉及主要液滴撞击行为计算,采用较细化网格剖分,如图3 (b)。

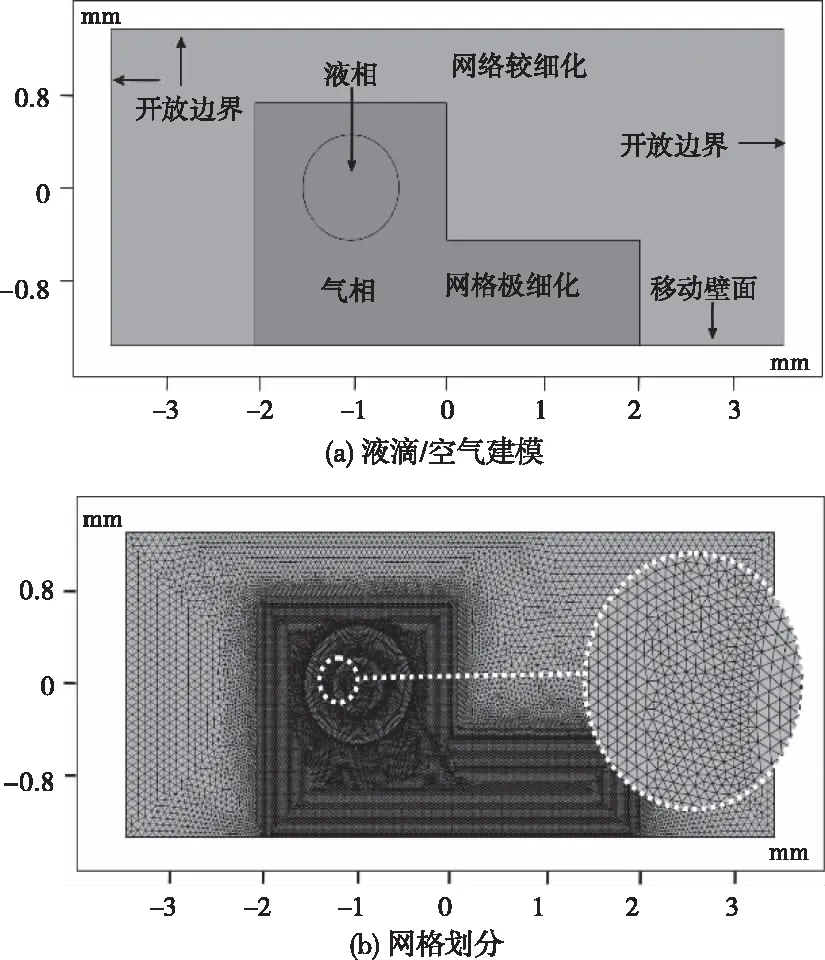
图3 液滴、空气模型及网格划分

3.2 两相流模型的数值求解

利用COMSOL中流体流动模块的两相流-层流接口,流体控制方程为动量守恒定律及质量守恒定律,基于相场对两相边界进行追踪、研究液体-气体二相流体的多物理场耦合,对其模型进行数值求解。

液滴与空气黏度采用COMSOL内置函数eta (T),T为温度,取293.15 K,液滴为水,动力粘度为μw=0.001 Pa·s,密度ρw=998.6 kg/m3。空气动力粘度为μa=1.813*10-5Pa·s,密度ρa=p*0.02897/R/T,p为压强,R为摩尔气体常数。液滴与空气表面张力系数为7.25·10-2N/m,润湿壁的接触角为90°。

3.3 边界条件

设置符合实际情况边界条件,利用有限元法计算动量方程及连续性方程。下边界设定壁面移动恒定速度A,其余边界设定为开放边界,气体可以随意流入流出,即液滴周围可看作无限大充满空气的区域。

3.4 网格独立性验证

为验证仿真结果可靠性及网格划分的合理性,且液滴铺展性能直接影响液滴撞击壁面结果,本文通过比较不同精细度网格划分下液滴铺展直径的偏差,选择计算时间少且精细度高的网格。对图3 (a) 蓝色与灰色区域以不同精细度进行网格划分,把蓝色区域网格划分分为极细化、超细化、较细化、细化、常规,灰色区域的网格划分精细度小于等于蓝色区域。

取计算时间步长值为0.00005 s,计算0～0.005 s液滴撞击壁面过程。图4(a) 为不同网格划分与液滴最大铺展直径关系;图4 (b) 为计算时间与液滴最大铺展直径关系。由图4可知,选择蓝色区域为极细化、灰色区域为细化或较细化,在保证计算精确度的情况下大幅减少了计算时间。本文按此方法进行网格划分,完整网格含有67592个域单元和1074个边界单元;大大提减少计算机运算量,且边界单元格减少将提高模型的收敛性与稳定性。

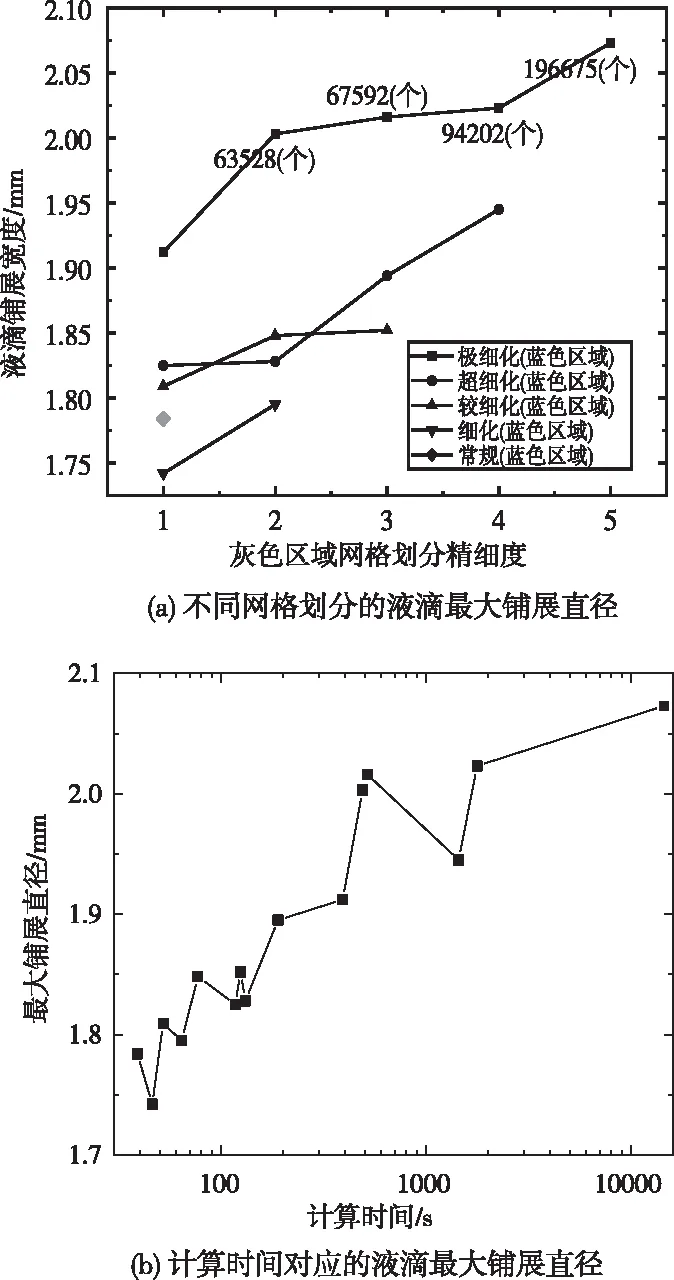
图4 网格划分、计算时间与液滴最大铺展直径关系

4 结果讨论

4.1 液滴下落回弹仿真分析

设置液滴从高度h0下落,为提高计算效率,对液滴施加初速度v0,满足

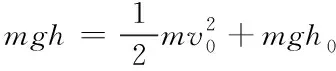
(10)

等效于液滴从h=10、20、30、40、50、60、70、80、90、100mm处下落,液滴初速度v0、使液滴弹起的壁面移动临界速度如表1。

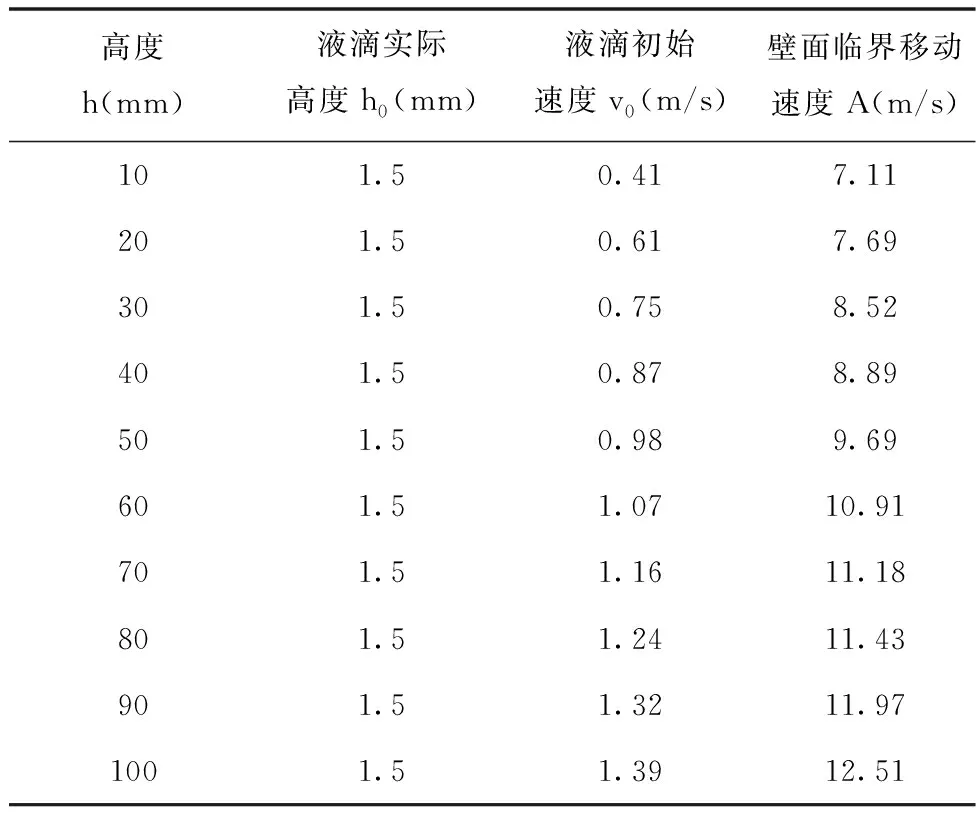
表1 等效高度与壁面移动临界速度关系

基于二分法寻找各等效高度h使液滴弹起的壁面移动临界速度,另加一组高度为10 mm,壁面运动速度为0 m/s、空气动力粘度为0 Pa·s及空气密度恒为1.29 kg/m3对照组作为比较。

仿真分析结果如图5所示,其中:图5 (a) 壁面没有移动时液滴下落直接与壁面接触,接触角90°为非疏水性壁面,液滴与壁面间粘连、能量被耗散,液滴未弹起;图5 (b) 壁面移动时带动空气流动形成流场,流场使液滴形变、横向铺展,并与地面形成一定夹角,由于流场阻挡液滴下方排开空气,液滴与壁面夹角形成的区域空气堆积且压强增大,使液滴弹起。图5 (c)、(d) 分别为空气动力粘度0 Pa·s、空气密度恒为1.29 kg/m3时对照组,与图5(b) 液滴下落、铺展形态相同,仅弹起后形态略有差别,因此液滴撞击壁面的极短时间内,可忽略空气黏度及空气密度变化造成影响。图5 (e)、(f) 液滴下落高度增加,液滴弹起的壁面临界移速相应增加,液滴形变增大,由于液滴下落时冲量较大导致部分液滴与壁面接触,与壁面接触的液滴随壁面移动,液滴中部发生断裂,剩余未随壁面移动的液滴在空气薄膜向上升力的作用下弹起。

图5 不同高度、不同壁面移速、不同黏度及密度的液滴下落演化过程

4.2 液滴动力学分析

图6 (a-d) 所示为壁面移动速度为10 m/s,液滴从高度h=30 mm下落,不同时刻液滴与空气的压力分布图。在t=0.0017 s时刻,液滴下端触及壁面,受流场影响发生形变,弧面变平且与壁面存在夹角,左侧存在向右流场,该区域气体出现堆积,气压变大(图6 (a))。在t=0.0026 s时刻,液滴在流场作用下变为扁平椭圆,液滴下端弧面与壁面夹角变大,与移动壁面接触部分出现脱离,造成质量损失,受壁面剪切力影响液滴中部出现低压区域,液滴铺展,空气薄膜形成 (图6 (b))。在t=0.0033 s时刻,液滴中部低压区域扩大,两端压强大于中部,产生向中部张力,液滴下方空气薄膜将液滴与壁面完全隔断,空气薄膜压力大于液滴上方空气,液滴开始向上运动 (图6 (c))。t=0.0040 s时刻,液滴在空气薄膜作用下弹起,受表面张力作用变为球状,表面能转化为动能,液滴弹起 (图6 (d))。

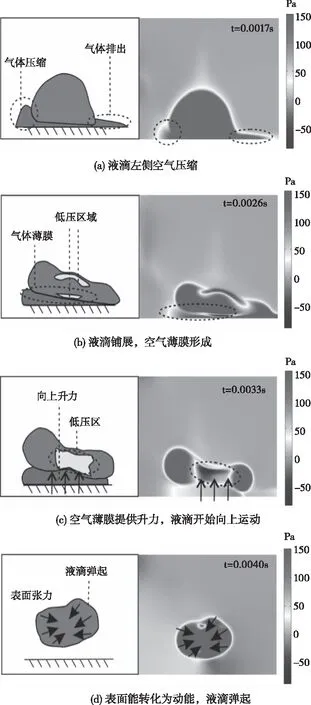
图6 液滴下落过程压力分布图

式 (9) 描述了形成空气薄膜时,流场速度与液滴下落高度关系,而流场速度是随距地面高度变化的函数,在工程实际中难以测量,得出下落高度与壁面移动速度的关系,对工程应用具有重要意义。

图7 (a) 为t=0.0001 s时速度分布,壁面带动其上方气体流动,产生稳定梯度流场。图7 (b) 为t=0.0017 s时速度分布,液滴接近壁面,流场阻挡液滴下方排开空气,液滴排开气体对流场有向左力作用,流场速度减小,部分流体反弹。

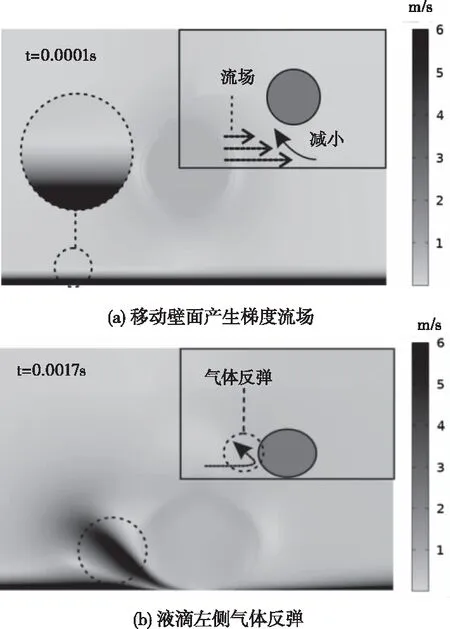
图7 液滴下落过程速度分布

求解牛顿粘性式 (11)

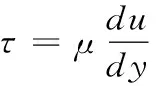
(11)

得图7 (a) 中壁面上方流体速度分布

Y(y)=Ae-σy

(12)

其中:μ为空气黏度,σ是与空气密度ρ呈正比、与空气黏度μ呈反比的系数,A为壁面移动速率,由于式 (11) 基于不可压缩牛顿流体求解,式 (12) 适用范围应远远小于100 m/s。图8中,空气薄膜进风口高度约为0.2 mm,对该高度以下流体速度进行积分,求空气流速平均值,可得该部分气流占总流场的0.8699。利用最小二乘法进行拟合,得A=15.8 m/s,σ=-10.2,拟合度 (R-squared) 为0.9817,标准差为0.2859。

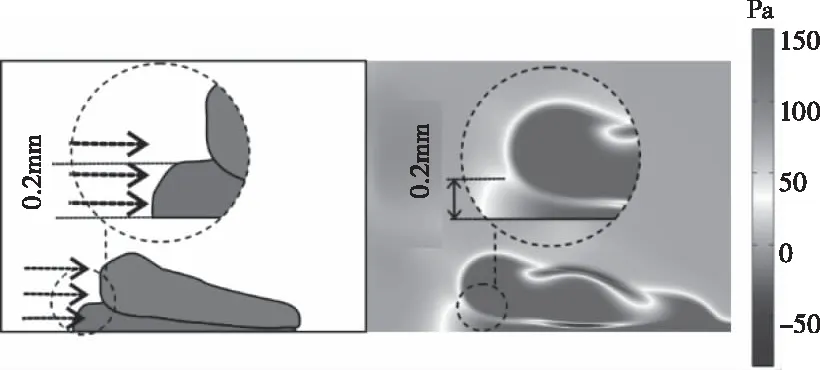
图8 空气薄膜高度

4.3 理论结果修正

液滴下端弧面与壁面间夹角θ表征液滴形变情况,壁面速度增大使液滴形变变大,θ变大。通过对仿真结果分析与测量,得到液滴与壁面夹角θ与壁面移动速度关系,在壁面移速为7.11 m/s时θ角较小,约为13.91°,在壁面移速为11.97 m/s时θ角达24.20°。图9为基于最小二乘法壁面移动速度与液滴夹角进行拟合,二者呈线性关系:θ=1.776u+3.066,拟合度为0.9141,式 (10) 应修正为:

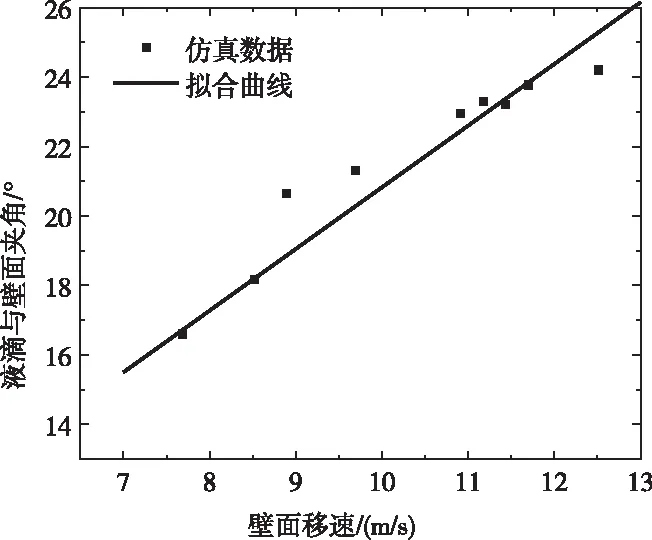
图9 壁面移速与液滴夹角仿真数据与拟合曲线

(13)

其中:θ=1.776u+3.066。

通过 (9) 式与仿真数据比对,计算得出拟合度为0.9592,理论与仿真结果对应较好,图10为使液滴弹起的壁面临界移动速度与液滴下落高度关系的仿真数据、理论计算修正前后数据。

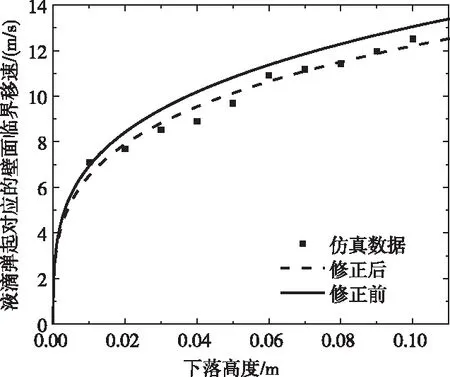
图10 仿真数据与修正前后数据比较

5 结论

本文对液滴撞击非疏水运动固体表面的液滴演化现象进行了分析,建立液滴-气体二相流体模型,通过数值模拟仿真探索了非疏水运动固体表面对液滴动力学行为,得到如下结论:

1)理论推导了液滴撞击移动壁时产生空气薄膜的临界气场速度,结合仿真数据拟合得到了优化的修正因子和壁面夹角的表达式,可量化描述液滴的铺展程度。

2)对液滴撞击非疏水运动固体表面的形成机理与液滴动态行为演变做出了阐述,稳定的空气使液滴与壁面间产生空气薄膜,空气薄膜减少液滴撞击运动固体表面能量损耗,为液滴弹起提供动力。

3)流场速度增大加剧液滴的形变,液滴与壁面夹角增加。壁面速度A、液滴与壁面夹角θ之间服从线性关系。

4)流场速度是随距地面高度变化的函数,在工程实际中难以测量,研究结果表明流场速度与液滴下落高度呈指数衰减关系,得出下落高度与壁面移动速度的关系,对工程应用具有重要意义。