基于ESO的高超声速飞行器姿态鲁棒控制

李大华,张紫依,吉月辉,刘俊杰*

(1. 天津理工大学电气工程与自动化学院,天津 300384;2. 天津市复杂系统控制理论及应用重点实验室,天津 300384)

1 引言

飞行器姿态控制器的设计是高超声速飞行器实现其飞行可靠性能的关键技术之一。俯仰、滚转和偏航等姿态运动是高超声速飞行器必不可少的运动,但由于其运动过程中具有快时变、强耦合、非线性以及不确定等特点,因此对姿态控制设计提出了极大挑战[1-3]。

面对这些挑战,近些年各位学者运用了预测控制、动态逆控制、滑模控制、鲁棒控制、自适应控制等多种控制策略。文献[4]基于高超声速飞行器研究并提出了自适应动态面控制方法。文献[5]结合反步法和动态逆控制技术对姿态纵向模型进行控制设计。文献[6,7]分别在滑模控制和反步控制的基础下研究并提出了一种高超声速飞行器的自适应容错姿态控制律。文献[8]将姿态系统分为了内部子系统和输入输出子系统,并研究提出了非最小相位的鲁棒自适应神经控制。文献[9]研究了一种基于扰动估计的姿态跟踪控制方法。文献[10]利用滑模、自适应、神经网络提出了近空间高超声速飞行器鲁棒跟踪控制。文献[11,12]分别针对高超声速再入飞行器,研究并提出了基于反步的终端滑模控制方法。文献[13]针对高超声速飞行器飞行轨迹和姿态控制在六自由度模型框架下提出了深度神经网络的控制方法。文献[14]研究了自适应和坐标变换技术,提出一种输出约束非仿射的控制策略。文献[15]采用了凯恩方法建立了高超声速飞行器的姿态运动学方程,在此基础上提出了一个基于反步法的滑模姿态控制思想。文献[16]提出了基于切线障碍的控制方法,并采用鲁棒预测控制技术对高超声速飞行器全状态约束进行姿态跟踪。文献[17]提出了一种综合的控制方法,在高超声速飞行器纵向模型的基础上建立含有扰动的二阶系统故障模型,并设计快速自适应终端滑模控制器。

上述文献中所用的控制方法大多需要基于完整并且精准的数学模型,对模型的依赖性较强,但是高超声速飞行器的模型不确定性比较强,上述方法对其难以获得较好的控制效果。而自抗扰控制技术中的扩张状态观测器能解决此问题,它能将模型不确定性所带来的扰动进行实时估计和补偿。本文基于扩张状态观测器做出了如下贡献:

首先,采用扩张状态观测器对高超声速飞行器姿态通道间的耦合、参数不确定性以及外部扰动等进行估计补偿;其次,采用神经网络最小参数学习法设计自适应控制器,消除系统姿态角的跟踪误差,提高系统控制精度,并增强系统的抗扰能力。

2 六自由度运动模型

本文采用的是NASA兰利研究中心给出的高超声速飞行器Winged-cone结构模型,它的六自由度模型完整运动方程由下述方程组表示[19]

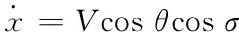
(1)

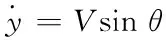
(2)

(3)

(4)

+LcosγV-NsinγV-mgcosθ

(5)

+LsinγV+NcosγV+mgsinθ

(6)

(7)

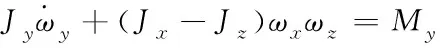
(8)

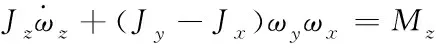
(9)

(10)

(11)

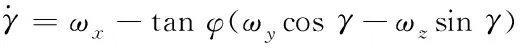
(12)

sinβ=sin(ψ-σ)cosγcosθ

+sinφsinγcos(ψ-σ)cosθ-cosφsinγsinθ

(13)

sinαcosβ=cos(ψ-σ)sinφcosγcosθ

-sin(ψ-σ)sinγcosθ-cosφcosγsinθ

(14)

sinγVcosθ=cosαsinβsinφ

-sinαsinβcosγcosφ+cosβsinγcosφ

(15)

其中,m,V,g分别为飞行器的质量,速度,及重力加速度;θ,α,β,γV,σ,φ,ψ,γ分别为飞行器的弹道倾角、攻角、侧滑角、速度倾角、弹道偏角、俯仰角、偏航角以及滚转角;ωx,ωy,ωz分别为飞行器运行时绕x轴、y轴、z轴的转动角速度;Jx,Jy,Jz分别为飞行器绕x轴、y轴、z轴的转动惯量,其各自的导数分别为各转动惯量的变换率,该变换率受质量变换的影响;Mx,My,Mz分别为飞行器滚转通道、偏航通道、俯仰通道的气动力矩;T,D,L,N分别为飞行器的推力、阻力、升力和侧力。相关的气动力和气动力矩表达式可参考文献[19]。

3 姿态角控制器设计

3.1 扩张状态观测器设计

将欧拉角微分式(10)至式(12)中的各通道间的角速度耦合视为扰动误差Ex,Ey,Ez则欧拉角动态可表示为

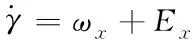
(16)

(17)

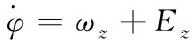
(18)

且

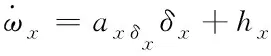
(19)

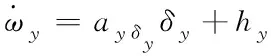
(20)

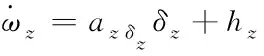
(21)

其中,axδx,ayδy,azδz分别为三通道各自的稳态控制增益,hx,hy,hz则表示各个通道间的扰动误差。

再将微分方程(16)至(18)求导,可得欧拉角和控制输入舵偏的关系式

(22)

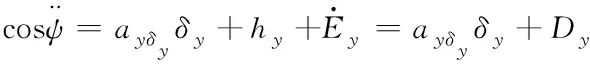
(23)

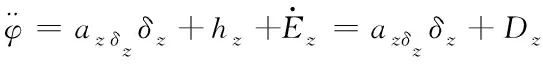
(24)

其中,Dx,Dy,Dz是各通道间的总扰动。

基于上式,分别为俯仰通道、偏航通道、滚转通道设计了三个降阶ESO为

(25)

(26)

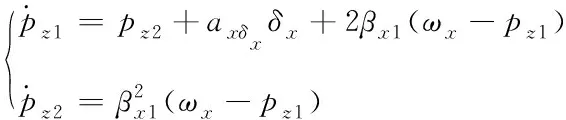
(27)

其中,qz1,rz1,pz1分别为俯仰角速度、偏航角速度、滚转角速度的估计值;qz2,rz2,pz2分别为三通道各个总扰动的估计值;βk1(k=x,y,z)为观测器的增益。

3.2 神经网络最小参数学习法自适应控制器

以俯仰角为例进行控制器设计,考虑高超声速飞行器的俯仰角控制,俯仰角的微分动态可以表示为如下二阶非线性系统

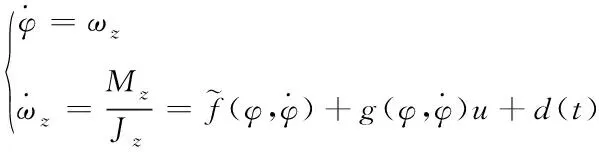
(28)

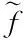
e=φ-φd

(29)

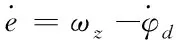
(30)

设计切换函数为

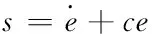
(31)

其中,c>0,于是

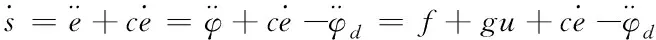
(32)

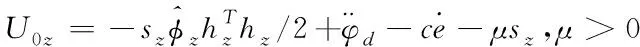
(33)

同理可得,偏航角和滚转角的自适应控制律为

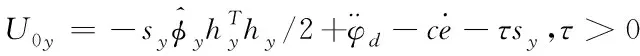
(34)

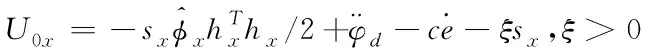
(35)

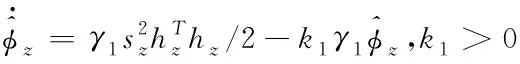
(36)

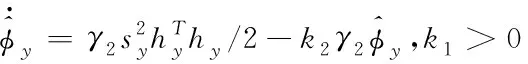
(37)

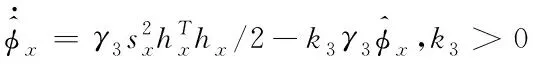
(38)

则,最终的姿态控制律表达如下所示

(39)

3.3 稳定性分析

定理1:考虑系统(10)(12),在式(39)所示自适应控制律式和式(36)(38)所示自适应律式的作用下,俯仰角φ、偏航角ψ和滚转角γ的控制是渐近稳定的。

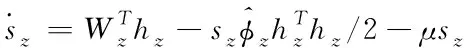
(40)

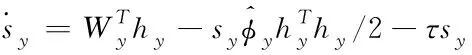
(41)

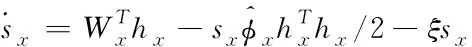
(42)

定义Lyapunov函数如下

L=L1+L2+L3

(43)

其中,L1,L2,L3的表达式如下所示

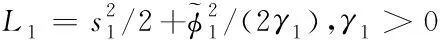
(44)

(45)

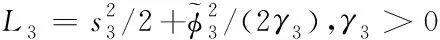
(46)

对L求导,求导整理可得

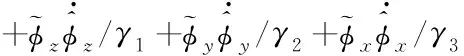
(47)

将式(47)进行推导,整理化简可得

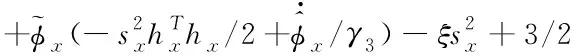
(48)

将自适应律式(36)(38)代入式(48)化简得

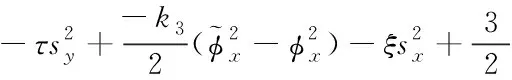
(49)

取

k1=2μ/γ1,k2=2τ/γ2,k3=2ξ/γ3

(50)

将式(50)代入式(49)中,进一步可得

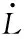
=-2μLz+Q1-2τLy+Q2-2ξLx+Q3

(51)

此处,采用不等式求解定理式(52)解不等式(51)

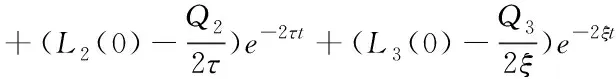
(52)

最终整理为

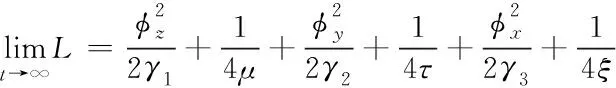
(53)

定理证毕。

4 仿真研究

将本文所提方法与传统线性自抗扰控制方法进行对比。采用本文方法的控制器参数如下

azδz=2、ayδy=2、axδx=2.45、βz1=5、βy1=5、βx1=5、c=8、bj=1、τ=15、μ=15、ξ=15、γ1=0.2、γ2=0.2、γ3=0.2、cj=[-2-1 0 1 2;-2-1 0 1 2]。俯仰角和滚转角的设定值是周期为20s,幅值为5弧度的信号,偏航角的设定值为0,在第五秒至六秒的时间段内在φ上加了0.005弧度的扰动。仿真结果如图1至图3所示。

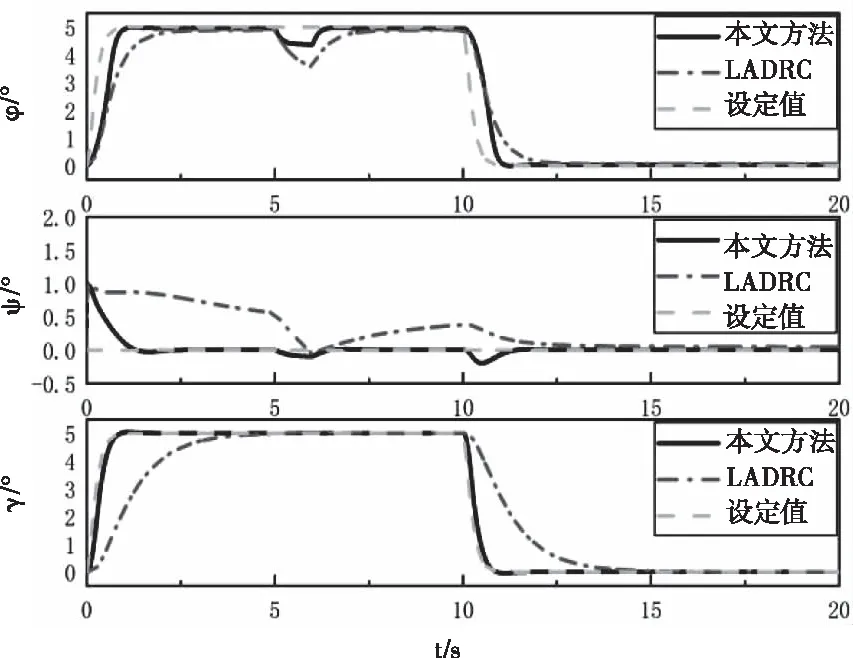
图1 姿态角跟踪曲线

图2 角速度跟踪曲线

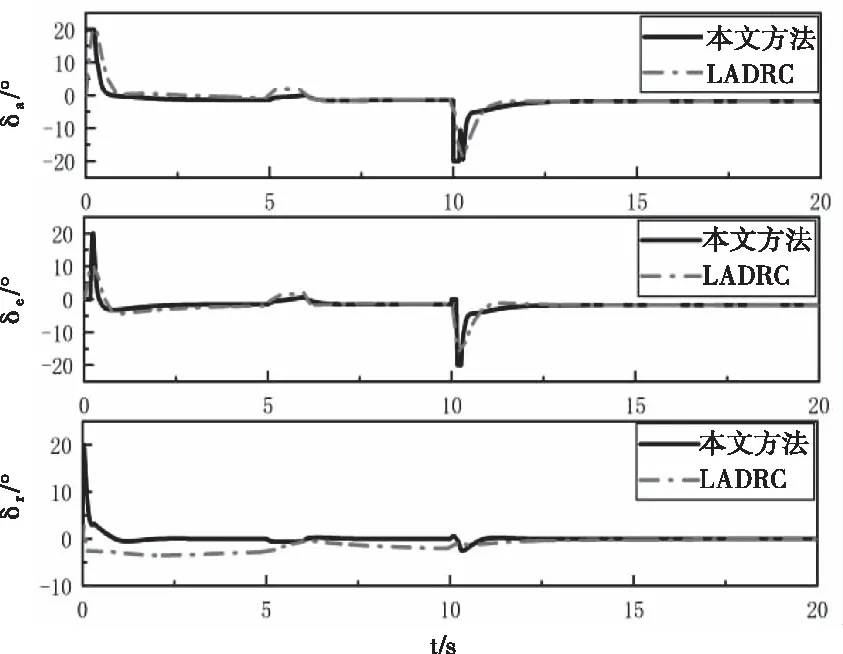
图3 舵机跟踪曲线

图1至图3中本文控制方法相比于传统线性自抗扰控制方法而言抗干扰效果好,且受干扰后能快速恢复稳定。如图1所示,可看到本文控制方法下的俯仰角在第5秒开始数值变成4.4弧度,在第6秒左右重新跟踪上设定值,而LADRC在有扰动的情况下数值变成3.5弧度且在第7.5秒才恢复稳定,表明本文所提方法抗干扰能力好。

5 结论

本文针对NASA公布的高超声速飞行器六自由度模型,针对其姿态控制问题,提出了一种基于ESO的姿态鲁棒控制方法,用扩张状态观测器对总扰动进行补偿估计,再结合神经网络最小参数学习法减少系统跟踪误差,并采用李雅普诺夫理论进行控制器闭环稳定性分析,最后通过数值仿真验证了所提控制策略的有效性。