基于级数法的热弹各向异性层合板兰姆波频散特性分析1)

吕 炎 林晓磊 高 杰,2) 何存富

* (北京工业大学信息学部,北京 100124)

† (北京工业大学材料与制造学部,北京 100124)

引言

随着材料科学的不断发展,单向纤维复合材料因其具有高强度、耐热性等优势广泛应用于航空航天、电子信息等领域[1-3].然而,复杂的服役工况将致使各向异性单向纤维材料易出现分层或裂纹等典型缺陷,严重影响材料的综合性能.当前,考虑到声波在材料传播过程中携带着大量的材料信息[4],且超声检测法具有厚度可层析及现场可操控等优势,促使其成为了材料缺陷检测较为有效的无损检测手段[5].其中,准确获取复杂工况(如含温度场等)波导结构中导波的传播特性是实现材料内部缺陷声学表征的重要前提.

当前,众多学者针对波导结构中超声导波频散曲线的数值计算方法开展了研究,其中矩阵法是处理层状介质中波动问题的经典方法,如全局矩阵法[6]、刚度矩阵法[7]和散射矩阵法[8]等.然而,随着多层介质层数的增加,矩阵法易产生数值不稳定的现象,造成明显的漏根和错根现象[9-10].为了避免上述勘根算法的弊端,Lefebvre 等[11]提出了勒让德多项式展开法来叠加拟合位移分量,将传统的超越方程求解转换为了特征值问题的处理,实现了多层介质超声导波传播特性的数值计算.随后,Wang 等[12]将勒让德多项式法拓展应用至功能梯度材料,压电半导体材料[13],分数阶热弹板[14]等复杂波导结构中的超声导波频散特性理论计算分析.然而,当提高截止项阶数以克服逐渐凸显的大频厚积问题时,矩阵维度的增加及冗余的积分运算致使运算成本大幅度提升,而较低的截止项将导致数值计算结果难以收敛.

与此同时,材料的热力学性质亦将影响声波的传播特性.李妍等[15]研究了半无限大薄板热弹扩散瞬态响应问题,着重分析了薄板温度、应力和浓度等物理量随热时间及扩散时间迟滞因子等参数变化的分布规律.Toki 等[16]利用薄壳理论,数值模拟了热环境下碳纤维增强复合材料的振动特性,并揭示了其与纤维体积、纤维方向和温度变化等因素间的作用机理.吴楠等[17]研究了极低温度环境下碳纤维复合板的热变形机理,并仿真分析了影响热变形特性的主要因素.在处理热弹性材料中的导波传播问题时,Green 等[18-20]发展了无能量耗散的热弹性线性化理论,基于此着重分析了弹性固体中的无阻尼热波,同时,对热力学中材料本构方程的基本假设进行了新检验.随后,Qahtani 等[21]利用势函数法求解了热弹性氮化硅板中导波的频散曲线,并利用半解析有限元法进行了对比验证.Verma 等[22]利用广义热弹性理论,详细推导了平板结构的对称模态和反对称模态对应的频率特性方程,并数值模拟了热弹性波在薄板中的频散和能量耗散特性.Li 等[23]通过结合二维高阶谱元与有限元方法,提出了无能量耗散的热弹性波在空心圆柱中传播的波动方程修正公式,并考虑了谱元阶数的影响,以数值分析空心圆柱结构中声波的频散特性.Wang 等[12]和Yu 等[24-25]通过联立G-N 理论与勒让德级数联合法,数值分析功能梯度板结构在自由应力及等温边界条件下的导波频散特性,并对比分析了非均匀热弹性板和纯弹性板导波频散曲线的分布规律,并将其拓展应用至处理热弹性弯曲板的波动问题[25].随后,提出一种改进的勒让德正交多项式方法,以求解分数阶热弹板中的导波传播问题[12],着重分析了分数阶次对频散、衰减曲线等的影响.此外,Dodson 等[26]基于实验获取的铝合金板不同频率下的群速度以及群速度温度敏感性曲线,深入探究了兰姆波波速在不同温度下的变化.Gandhi 等[27]建立了受双轴均匀应力场作用的各向同性介质的声弹性兰姆波传播理论,指出频散曲线在大多数应力、模态和频率下呈现各向异性变化.基于上述研究,Yang 等[28]提出了一种结合半解析有限元方法的热声弹性理论,探究了均匀和非均匀热效应对声弹性导波传播的影响.为了提高理论建模的准确性与求解效率,依然需要发展更为可靠的计算方法来探究温度场下各向异性层合板中的导波传播特性.

为了避免传统级数法中冗余的积分运算,实现多种复杂波导结构中高频波动问题的精确求解,本文提出了状态矩阵与勒让德多项式联合法.理论建模方法的核心在于: 通过引入状态矩阵法,将控制方程、几何方程及本构方程以状态矢量的方式进行表达,即引入状态矢量矩阵将相关参数矩阵转化为上三角矩阵和对称矩阵,可实现复杂波导结构中频散方程的推导;并运用勒让德级数的正交完备性及递推特性,并导入多个线性因子的积分表达式解析解,将频散方程的求解问题转换为特征值求解问题,以此克服传统勒让德级数法高截止项的计算难题,并解决传统矩阵方法求解数值不稳定所带来的模态错位及漏根问题[9-11].本研究将其拓展应用至温度场状态下各向异性层合板中热弹波的频散特性数值分析.通过建立各向同性层合板的声学频域仿真模型,验证了所提理论方法的正确性.最后,建立了三层单向纤维复合材料层合板的导波传播特性理论模型,细节分析了堆叠顺序、温度变化对单向纤维层合板中导波传播特性的影响规律.

1 理论分析

1.1 声传播理论模型

针对第z层碳纤维材料,对应的局部坐标系可表示为().此时,x1与x1z之间的旋转角φ即为第z层材料在全局坐标系中的方位,而相应的弹性常数表达式可整理为

基于小变形假设,材料的应力应变关系可整理为

为模拟含温度场的多层碳纤维层合板中兰姆波的传播特性,基于无体力的线弹性材料,引入了Green-Nagdhi 热弹性理论[18-20],此时热弹性材料的波动方程可表示为

其中,σijz为应力分量,εijz为应变分量,uiz为位移分量;Cez为恒定应变下的比热,T0z为参考温度参数,Tz为温度参数.随后,将第z层材料的位移及应力分量整理为状态矢量的形式,以实现未知参数的同步简化求解

其中,kz和ωz为波数和角频率分量,T表示温度的幅值.此时,波动方程可重新整理为

同样地,本构关系可重新表示为

其中,Dijz为由力学参数组成的系数矩阵.随后,将式(7)中沿x2方向的应力表达式转换成位移变量形式,并代入至x1方向的应力表达式,可得

将其整理为矢量矩阵形式,并联立x2方向的应力表达式的向量形式,即

可推导得出第z层的状态矢量常微分方程

其中

将式(9)代入式(10)中,即可得到简化后的频散方程

其中,ς=k/k0表示归一化的相对波数.

1.2 勒让德多项式展开

将含有位移及温度分量的A矢量以勒让德多项式叠加拟合的形式进行展开,可表示为

式中,Pn(χ)为第n阶的勒让德多项式,当勒让德级数的截止项为n时,表示z-th 的两个方向位移分量幅值un,vn以及温度幅值Tn,N为勒让德多项式的截止项阶数.考虑到勒让德级数的有效作用区间为χ∈[-1,1],因此有必要对x2进行坐标转换

随后,将式(13)～式(15)代入至式(12),并对其进行正交投影,可以得到线性方程组

由于矢量线性算子的偏导影响,使得勒让德多项式的下标n与m的有效范围缩减为[0,N-2]及[0,N-3].此时,上述线性方程组仅能提供3(N-2)个方程,难以实现3N个未知幅值及温度量求解.因此,考虑了界面处的自由应力边界条件,以及层间界面处应力与位移的连续性边界条件

随后,将线性方程组与边界条件进行结合,即联立式(16)～式(18),以推导得出完整的频散特征线性方程组

最后,通过MATLAB 中的eig 函数求解式(20)中的特征值(ϛ)与特征向量(E),即可实现含温度场的多层材料超声导波频散曲线、位移及应力波结构的同时绘制.

2 温度场下各向同性层合板导波频域仿真分析

2.1 声学频域仿真模型建立

借助COMSOL 有限元仿真软件,建立了温度场作用下多层各向同性材料的声学频域仿真模型,如图2 所示.在建模过程中,考虑利用固体传热模块来模拟温度场分布,同时赋予每层材料导热系数与恒压热容,同时在四周边界处施加热绝缘条件,上下界面设置自由温度边界.结合固体力学模块,赋予每层线弹性材料杨氏模量、泊松比和密度等力学参量,层间设置连续性条件,实现多层各向同性材料中导波传播特性的数值模拟.其中,上述模型中多层材料的堆叠顺序为铜/钢/铜,每层材料厚度均为1 mm,所需各层材料的性能参数如表1 所示.在模拟声传播过程中,考虑在模型两侧设置Floquet 周期边界[30],使得模型沿着长度方向无限扩展,以弱化声波沿长度方向的反射与折射效应.同时,采用三角形精细化网格分割,利用物理场控制网格序列类型,提高仿真计算的精度.最后,通过参数化扫描特征频率获取所需频率范围内的波数,进一步求解出导波相速度频散曲线.

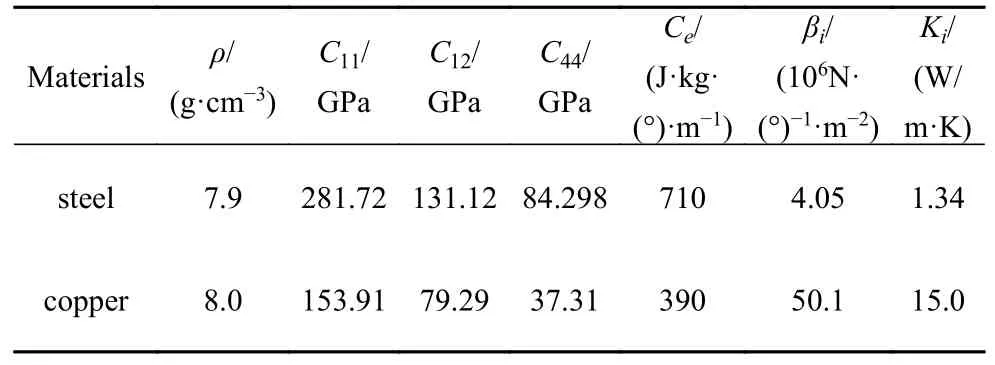
表1 钢与铜的性能参数[10,31]Table 1 Performance parameters of steel and copper[10,31]

2.2 理论与仿真结果对比分析

基于所建立的声学频域仿真模型,通过提取不同特征频率下的波数,数值计算了温度为293 K (20 °C)时铜/钢/铜层合板与3 层各向异性层合板的超声导波频散曲线,如图3 所示.其中,红色圆圈表示仿真计算的结果,黑色实线为所提理论计算得到的超声导波多模态频散曲线.可以看出,在低频范围内(0～1 MHz),仿真结果与理论数据均可以实现良好的吻合,有效地证明了所提理论模型的正确性和有效性.

3 温度场下各向异性层合板的声传播特性

基于G-N 热弹性理论及状态矢量与勒让德级数联合法,建立了由不同铺层方向单向纤维复合材料堆叠而成的各向异性层合板声传播特性理论模型,着重探究了堆叠顺序、温度变化对导波频散曲线及位移与应力波结构的影响规律,以验证所提方法的通用性和有效性.

3.1 堆叠顺序对导波传播特性的影响分析

以单向纤维增强复合材料T300/914 为研究对象,着重探究纤维取向对多层各向异性介质中导波频散行为的影响.其中,沿主轴方向单向纤维复合材料的力学性能参数如表2 所示.需要指出的是,当纤维铺层方向沿着不同角度分布时,可通过建立局部坐标系,以坐标转换的形式(即局部坐标系与全局坐标系的旋转夹角为φ)来描述对应材料的力学性能参数.随后,依据上述提出的理论方法,建立了相邻层铺层方向不同的3 层理论模型.其中,上下层单向纤维的铺层方向均沿主轴方向,即顶层和底层的纤维取向均沿着x1轴方向平行,并且中间层的取向角φ从0°到90°以30°的增量变化,以此形成了具有不同堆叠顺序的各向异性层合板理论模型.需要指出的是,每层单向纤维材料的厚度均为1 mm,所在温度场的温度为293 K.基于所提理论方法,数值计算了上述4 种理论算例的超声导波频散曲线,如图4(a)～图4(d)所示.

表2 单向纤维复合材料的性能参数[32]Table 2 Performance parameters of unidirectional fiber composites[32]

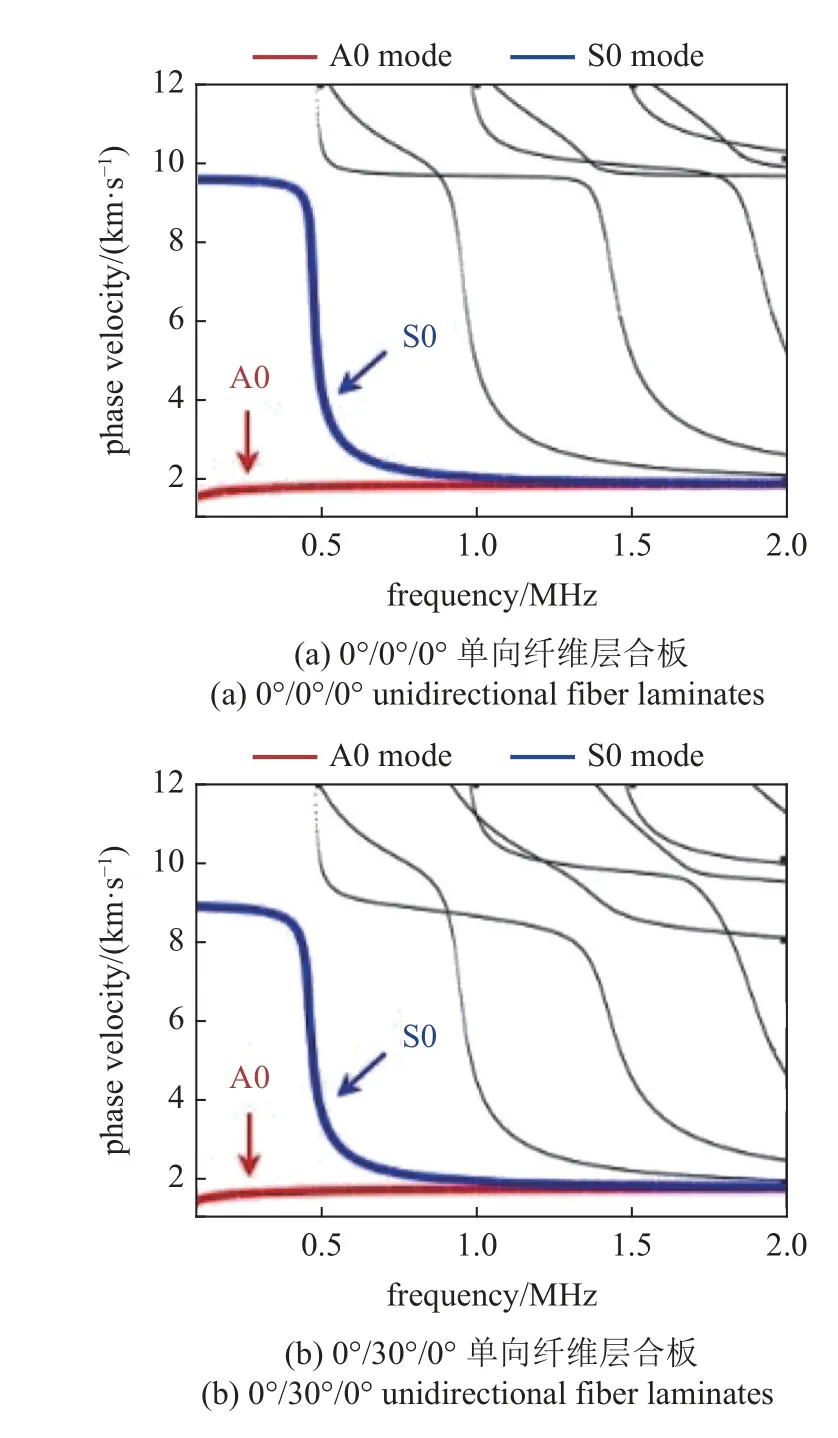
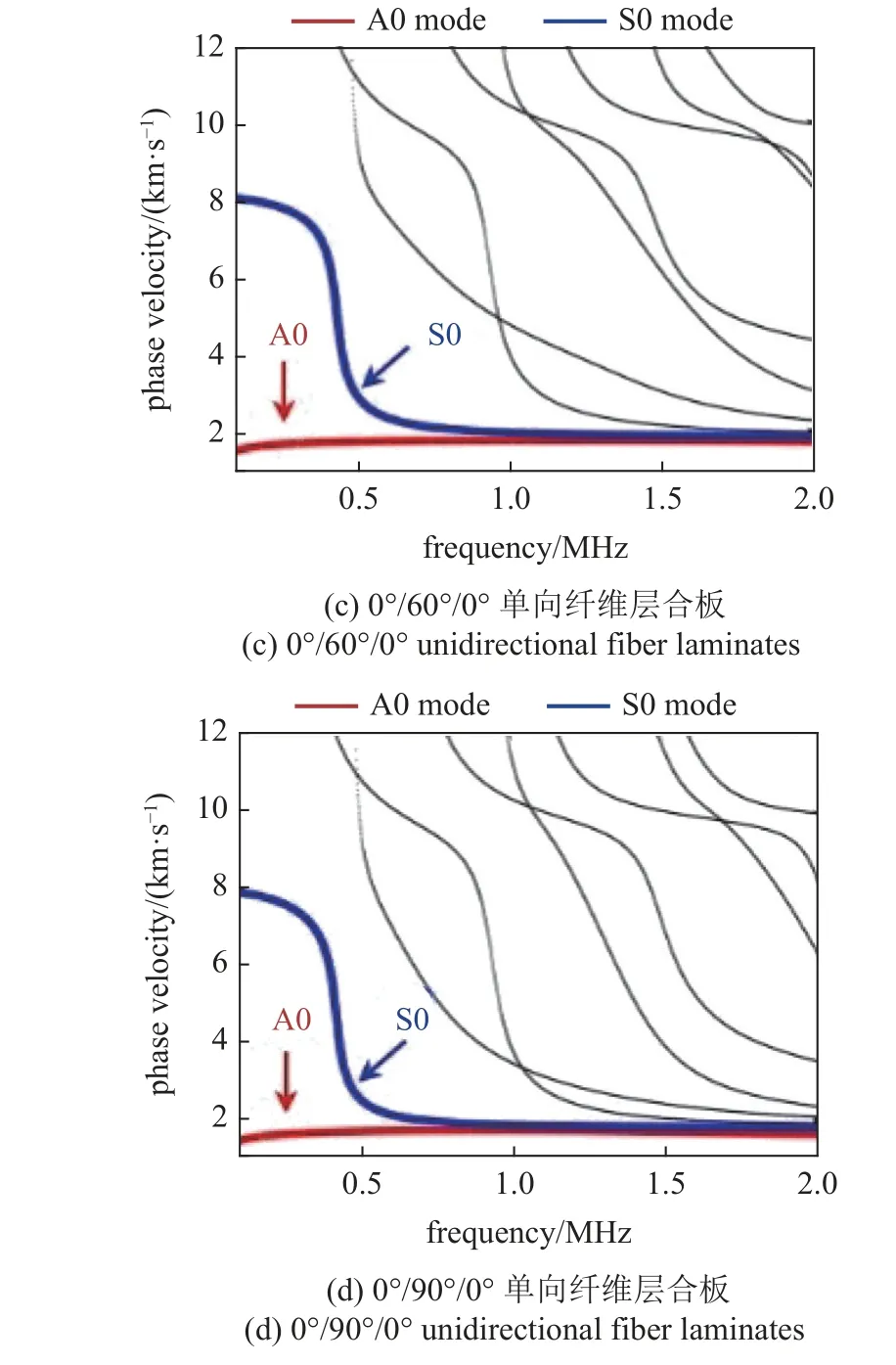
图4 不同堆叠顺序各向异性层合板导波频散曲线Fig.4 Guided wave dispersion curves of anisotropic laminates with different stacking orders

可以看出,在0～2 MHz 频率范围内,含温度场的各向异性层合板的多模态频散曲线均可以完整有效地绘制出来.其中,红色实线表示A0 模态,蓝色实线代表S0 模态,其余黑色实线代表高阶Lamb 波模态.通过对比可以看出,随着中间层碳纤维旋转角度的增加,相速度频散曲线的模态数量呈现出了递增的趋势,且整体逐渐向左偏移.与此同时,在截止频率处S0 模态的相速度值表现为大幅度降低的变化现象,而A0 模态的相速度值却并未呈现明显的偏移特征.此外,当单向纤维中间层的纤维角度不断增加时,高阶模态的截止频率亦不断向低频处偏移,对应的相速度值存在降低的现象.

3.2 位移及应力的波结构分布特征

通过求解式(20),可同步获取线性方程组的特征值(ζ)与特征向量(E).同时,将特征向量代入至位移及应力的表达式中,温度场下各向异性层合板中任意导波模态的位移及应力波结构均可以实现有效地重构.此处,以293 K 下堆叠顺序分别为0°/0°/0°与0°/30°/0°的单向纤维层合板为研究对象,绘制了1 MHz 频率处A0 模态的位移与应力的波结构分布曲线,如图5 所示.其中,红色虚线分别表示沿x1传播方向的位移与应力分布曲线,蓝色点划线分别表示沿x2方向的位移与应力分布曲线.

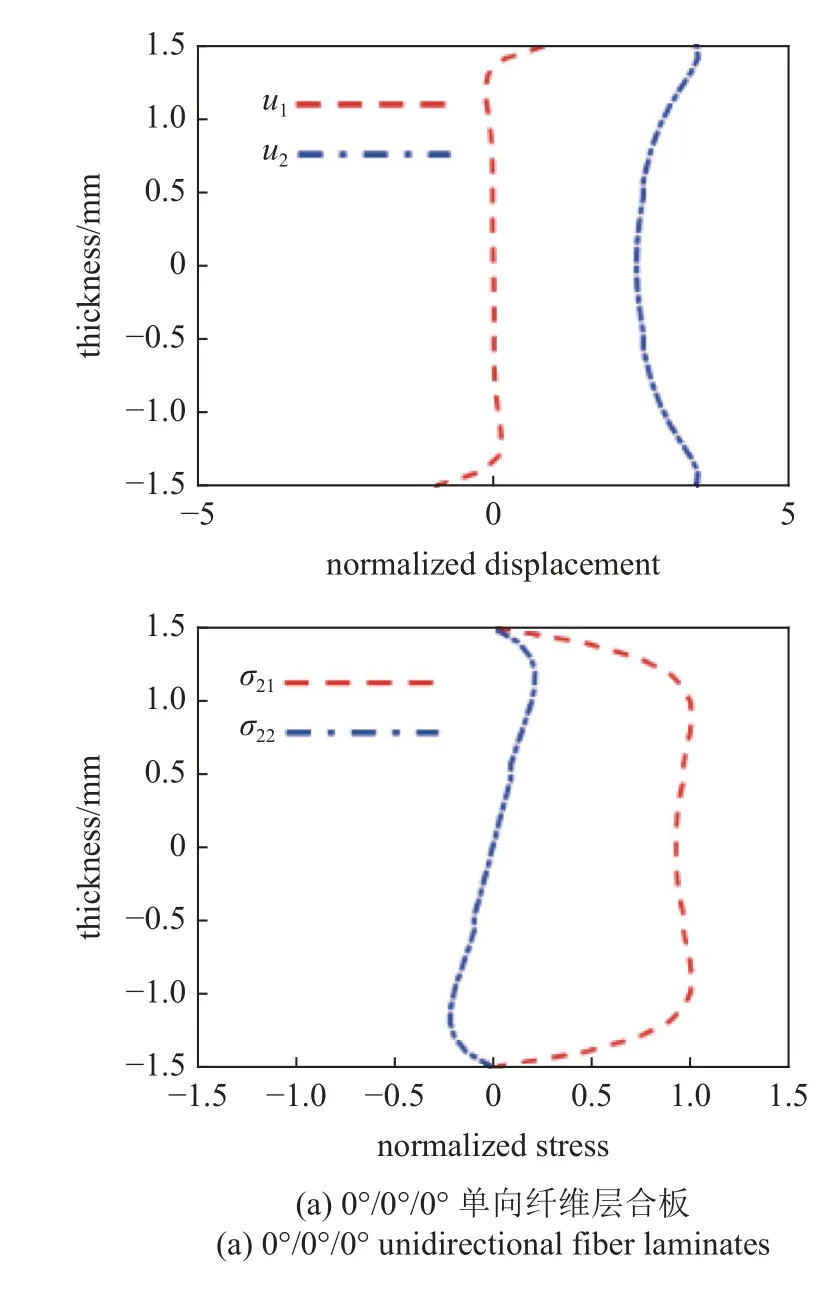
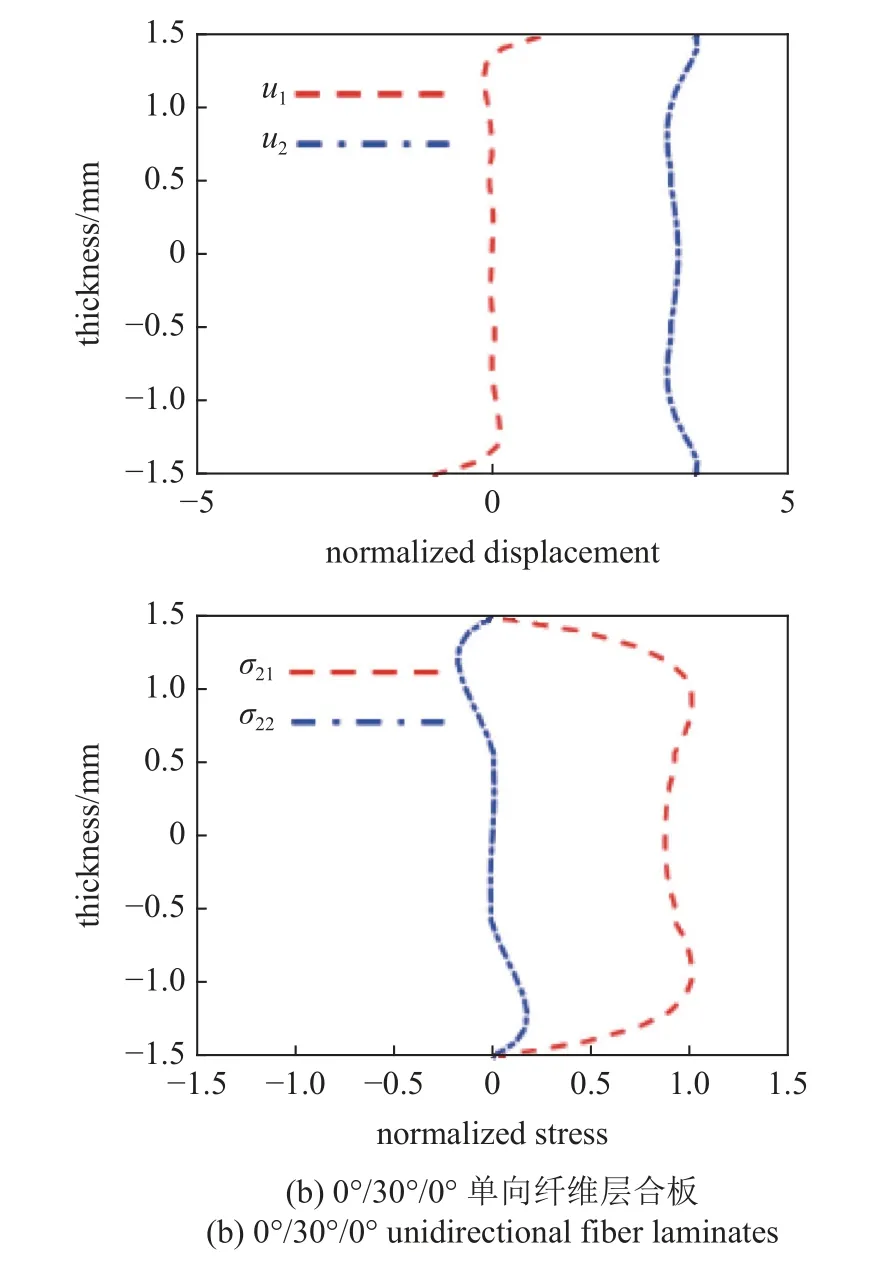
图5 293 K 下,0°/0°/0°与0°/30°/0°单向纤维层合板A0 模态位移与应力分布曲线Fig.5 A0 modal displacement and stress distribution curves for 0°/0°/0° and 0°/30°/0° unidirectional fiber laminates at 293 K

可以看出,对于A0 模态来说,离面位移u2关于中间层对称,而面内位移u1呈现反对称特性.其中,离面位移远大于面内位移,即A0 模态的质点振动将沿着厚度方向的离面位移为主占.同样地,正应力σ22关于中间层呈现反对称分布,而剪切应力σ21表现出明显的对称现象,且剪切应力远大于正应力.此外,在各向异性层合板的整个厚度范围内,两种堆叠顺序的单向纤维层合板的位移与应力分布曲线均呈现出了良好的连续性.尤其是在层与层的界面处,位移及应力均保持稳定的连续性.同时,上下界面处的应力值均为0,其与理论模型的预设边界条件一致.上述位移及应力波结构的分布特征有效地验证了所提方法的有效性.随着中间层纤维角度的增加,致使相邻层材料的性能参数的差异性逐渐增大.此时,位移与应力的分布曲线亦将呈现出明显的波动现象.

3.3 温度对各向异性层合板导波传播特性的影响

为了理论揭示温度变化对单向纤维层合板中超声导波传播特性的影响,基于所提理论方法,分别数值计算了堆叠顺序为0°/0°/0°与0°/90°/0°的单向纤维层合板的导波频散曲线.考虑到低频范围内的基础模态具有独特的弱频散特征,常作为超声导波检测技术的实验首选模态.为了便于分析温度对导波频散特征的影响,以低频范围内(0～0.5 MHz)基础模态的相速度频散曲线为例,着重讨论了温度变化与频散特征的内在关系,如图6 所示.其中,带有蓝色实心六角星形、五角星形、三角形、菱形、正方形、圆形的蓝色实线分别表示温度为293 K,323 K,353 K,383 K,413 K,443 K 时的S0 模态频散曲线,而带有红色实心六角星形、五角星形、三角形、菱形、正方形、圆形的红色实线分别代表了温度为293 K,323 K,353 K,383 K,413 K,443 K 时的A0 模态相速度频散曲线.通过对比可以看出,在给定的温度范围内,无论是A0 模态还是S0 模态的相速度值均呈现出了相应的变化规律.为了便于分析,分别将红色圆圈与蓝色圆圈所示范围的基础模态进行局部放大,如图6(a)和图6(b)所示.有趣的是,随着温度的逐渐递增,A0 模态相速度值均呈现均匀性的递减趋势;然而,S0 模态的相速度值却表现为非均匀间隔的递减现象,尤其是当温度从323 K 上升至353 K 时,S0 模态的相速度值出现了明显的突减现象,如图6(b)所示.因此,揭示温度场变化对超声导波传播特性的影响,可为含温度场各向异性层合板的内部缺陷或粘接状态等无损检测与评估提供理论指导.

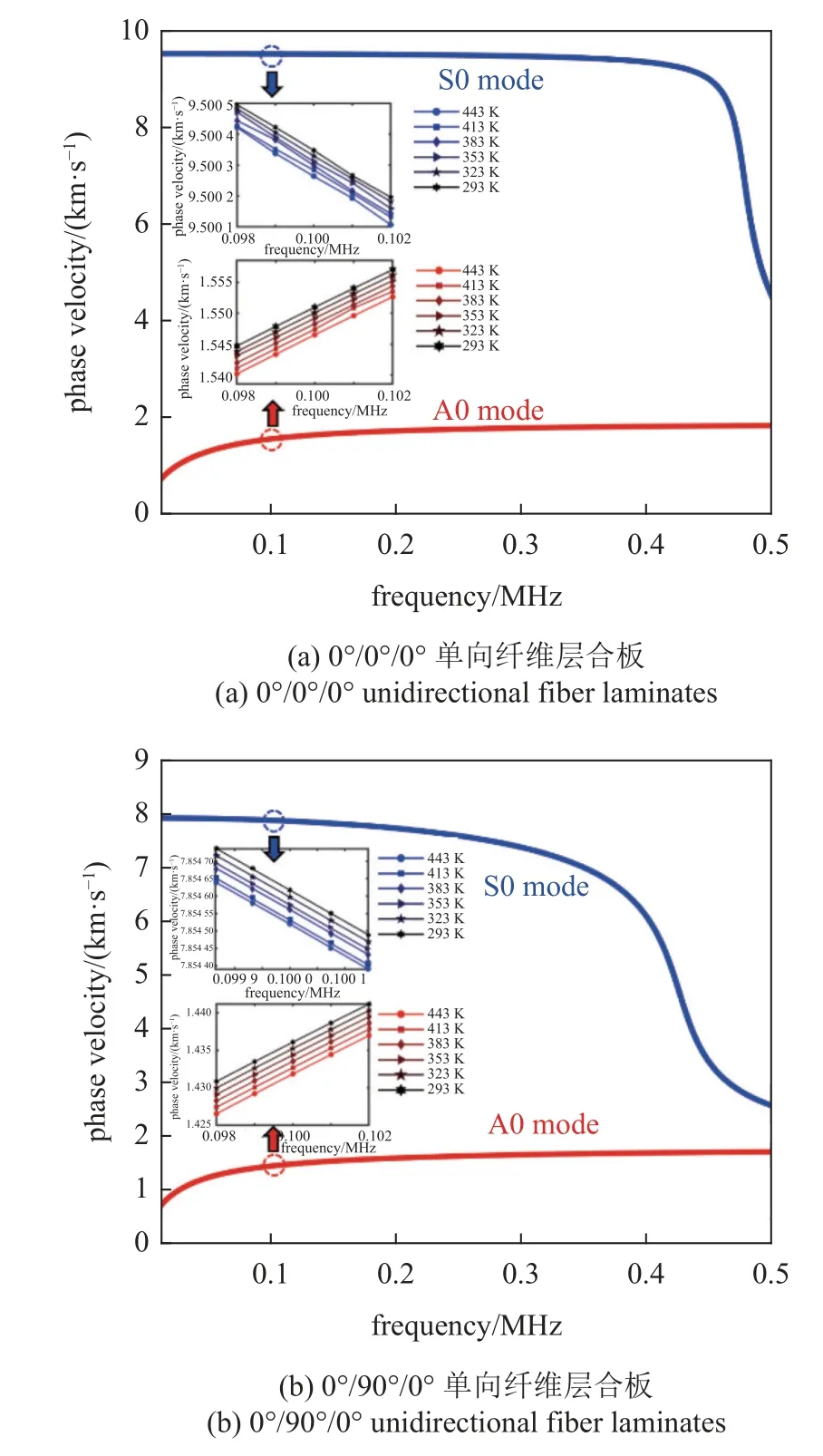
图6 不同温度下单向纤维层合板的频散曲线Fig.6 Dispersion curves of unidirectional fiber laminates at different temperatures

为了进一步量化温度对不同频率处基础模态的影响,详细列举了堆叠顺序0°/0°/0°与0°/90°/0°的单向纤维层合板A0 模态与S0 模态的相速度值,如表3 与表4 所示.可以看出,在任意频率处,基础模态的相速度值均随着温度的增加呈现出降低的趋势.

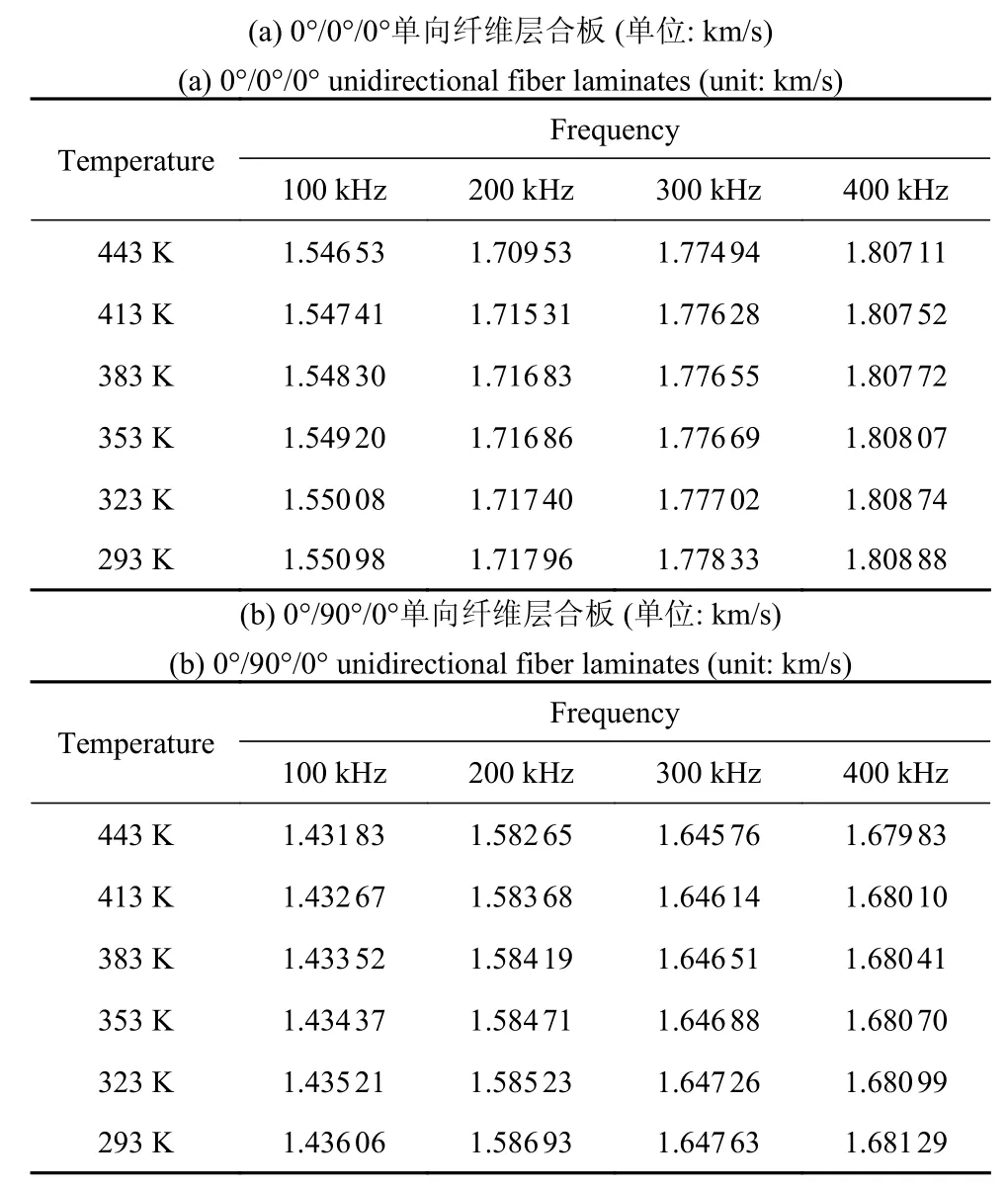
表3 不同频率与温度下的A0 模态相速度值Table 3 Phase velocity values of A0 modes at different frequencies and temperatures

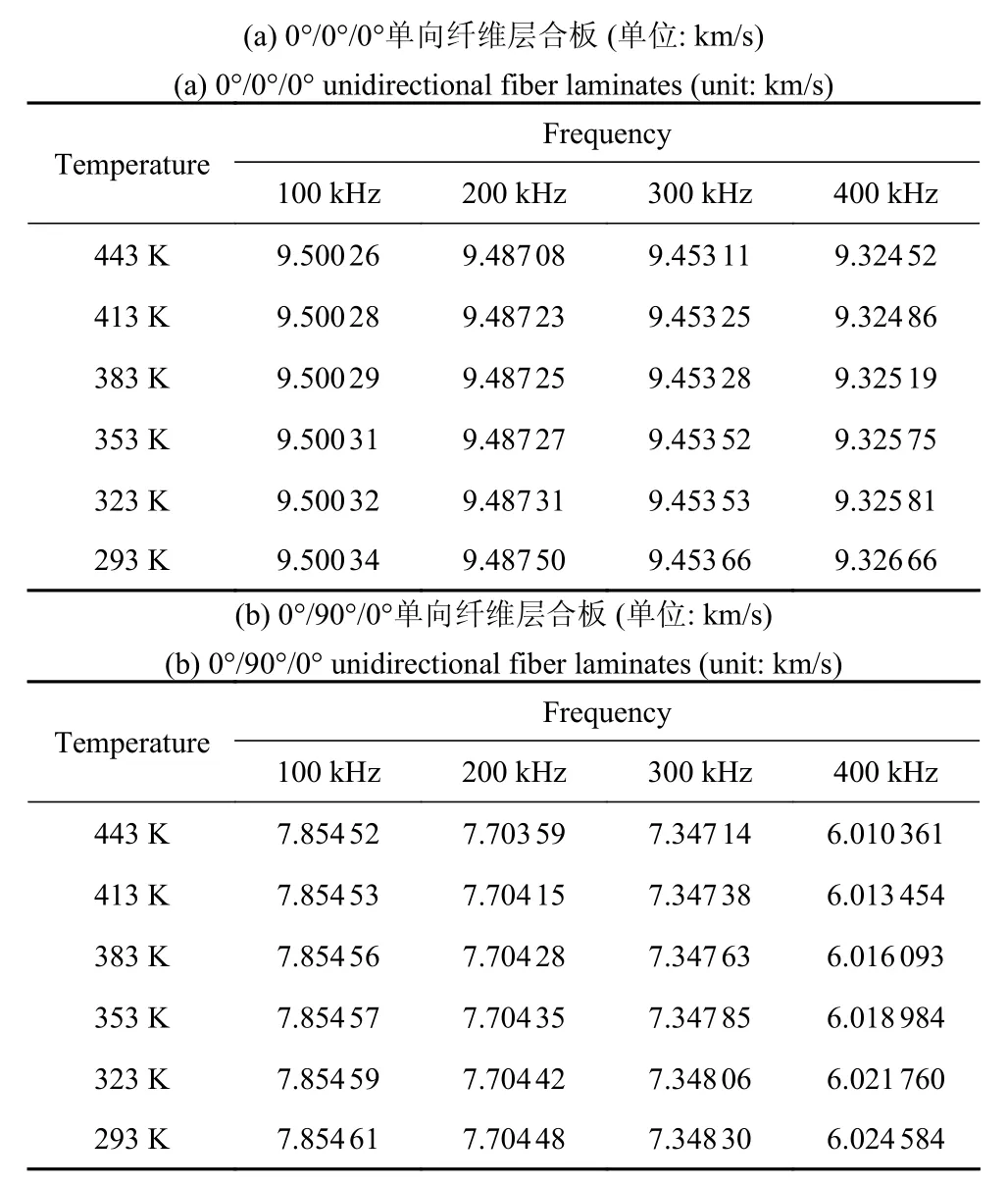
表4 不同频率与温度下的S0 模态相速度值Table 4 Phase velocity values of S0 modes at different frequencies and temperatures

3.4 各向异性层合板导波相速度温度敏感性分析

为了揭示不同频率下温度场变化对多模态相速度的影响规律,以堆叠顺序为0°/90°/0°的复合材料层合板为例,将温度场为493 K 的各向异性层合板的超声导波频散曲线与环境温度293 K 结果进行差值处理,以获取不同频率下不同模态的相速度温度敏感度变化曲线[28,33],如图7 所示.可以看出,在0～1 MHz 频率范围内的相速度温度敏感度均为负值,且对称与反对称模态的导波相速度温度敏感度均呈现一定的频散现象.其中,对于反对称模态来说,高阶模态A1 与A2 比基础模态A0 对相速度的温度敏感性更高,且在高阶模态的截止频率处表现出了很强的相速度热敏感性.对于对称模态来说,S2 模态的截止频率处呈现出较强的相速度热敏感性.

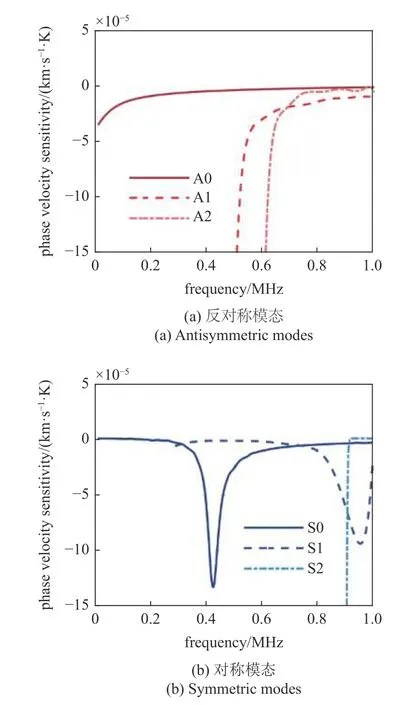
图7 不同频率下相速度温度敏感变化曲线Fig.7 Temperature-sensitive variation curves of phase velocity at different frequencies

4 结论

针对温度场下各向异性层合板结构中的超声导波传播特性分析方法,开展了理论及仿真研究,数值分析了温度场变化对各向异性单向纤维层合板中导波频散特性的影响规律,并得出以下结论.

(1)基于G-N 理论及状态矩阵与勒让德级数联合法,并考虑界面间的位移、应力与温度场的连续性边界条件和自由应力边界条件,构建了温度场下各向异性层合板导波传播特性的理论求解模型,实现温度场状态下各向异性层合板中导波频散曲线及波结构的同时获取.

(2)建立了温度场下的多层各向同性材料的有限元仿真模型,从频域角度分析了温度场环境下铜/钢/铜层合板中导波的传播特性,并借助所提理论方法,计算了相同结构的超声导波频散曲线,此时仿真结果与理论数值计算结果吻合较好.

(3)基于所提理论模型,着重分析了堆叠顺序、温度变化对3 层单向纤维层合板中超声导波传播特性的影响规律.结果表明,随着单向纤维层合板中间层旋转角度的增加,S0 模态相速度呈现明显的下降趋势,而A0 模态相速度的变化较为轻微.同时,因层间材料性质的差异,A0 模态的位移及应力分布曲线的波动性逐渐严重.此外,随着温度的逐渐升高,相比于S0 模态而言,A0 模态表现出了理想的均匀性递增趋势.

(4)以堆叠顺序为0°/90°/0°的复合材料层合板为例,分析了不同频率下多模态相速度的温度敏感度.结果表明,在0～1 MHz 频率范围内的相速度温度敏感度均为负值,且对称与反对称模态的导波相速度温度敏感度均呈现一定的频散现象.后续将在状态矩阵与勒让德级数联合法的基础上,将热应力引入至所提理论模型中,进一步揭示预应力场及温度场对热弹性导波传播特性的影响.