中国首座自制风洞关键技术参数再解读

李国峰 冯立昇

(1.内蒙古师范大学 科学技术史研究院,呼和浩特 010022;2.内蒙古科技大学 理学院,包头 014010;3.清华大学 科技史暨古文献研究所,北京 100084)

风洞(wind tunnel)自1871年由英国人弗兰克斯·赫伯特·维纳姆(Francis Herbert Wenham,1824—1908)发明以来,一直是飞行器研制及航空研究必需的实验设施。清华大学1936年建成中国首座自制风洞。学界对这座风洞的研制过程和取得的成就十分关注,做过许多研究和介绍[1-7],搞清了所涉机构、主要人员和具体过程等,但对《清华大学机械工程系之航空风洞》[8]、TheFirstChineseWindTunnel[9]、TheenergyratiooftheTsinghuawindtunnel[10]等核心史料的解读还不够细致。这些研究尽管注意到了这座风洞的雷诺数、能量比、扰流度和天秤感量等关键技术参数的数值颇为优秀,然而缺乏深入分析,未将雷诺数的理论值与实际值加以区分以致引起误读,亦未探寻能量比被清华风洞设计者最为重视所蕴涵的独特设计理念,也没有从关乎工作精度的扰流度和天秤感量等参数出发深究这座精密风洞对中国早期的风洞技术发展有怎样的贡献。本文在前人工作基础上做了进一步研究,获得了新的认识。

1 中国首座自制风洞：主体结构与关键技术参数

1932年,清华大学创建机械工程学系,下设飞机与汽车工程组,开始发展航空教育与学术研究。1933年8月,机械工程学系开始筹建航空馆与飞机库房、研制实验风洞等。工学院院长顾毓秀(1902—2002) 和机械工程学系主任庄前鼎(1902—1962) 指派王士倬(1905—1991) 负责筹建航空馆并设计风洞。1936年4月风洞建成,一般称为清华首座风洞(以下简称“清华风洞”)。清华聘请冯·卡门(Theodore von Krmn,1881—1963) 的学生、风洞专家华敦德(Frank L.Wattendorf,1906—1986) 制定风洞实验研究计划并负责风洞的运营。[9]七七事变爆发后,风洞毁于日军。

清华风洞主要包括洞体、风扇和发动机组成的驱动系统及天秤为核心的测量控制系统(图1)。洞体由直径粗细不一的实验段、扩散段、回流段和收缩段组成封闭环状(图2)。运行时风扇驱动气流在洞体内循环,流过悬挂在实验段内的待测模型,其受力情况由洞体外部的天秤实时测出。测试时,根据运动相对性原理,模拟飞行器的飞行。由于气流在洞内循环,故称回流式。用于测试模型的实验段直径1.52米(5英尺),可根据需要开、闭。该段气流均匀且速度最大,一般所说的风洞尺度与风速均指此处。[8]

图1 中国首座自制风洞外部侧视图(1)图1和图2,本文引用时添加了部分文字说明。[8]

对于清华风洞,评价其技术水平的关键技术参数主要有雷诺数(Reynolds number)(2)雷诺数是为纪念英国力学家、物理学家、工程师雷诺(Osborne Reynolds,1842—1912)而命名,记作Re,可用来表征流体的流动情况,判别粘性流体的流动状态,例如流体是层流还是湍流,也可用来确定物体在流体中运动时所受到的阻力。、能量比(energy ratio)、扰流度(turbulence degree)及天秤感量4项,分别反映风洞3个不同方面的性能。

雷诺数的物理意义是物体在静止空气中运动时所受到的惯性力与粘性力之比。气动特性中与粘性有关的现象,诸如附面层流态、气动阻力、分离流动与失速特性、激波与附面层相互干扰等,都受雷诺数的影响。风洞实验中,要求保持模型与全尺寸飞行器飞行状态的相似,雷诺数相似是一条重要准则。对于规模较小的风洞而言,实验一般采用缩比模型,因此实验雷诺数往往小于飞行器飞行雷诺数。欲使用实验结果,必须将其修正到飞行雷诺数。但是,将实验雷诺数修正到飞行雷诺数,其过程比较复杂,故而设计风洞时力求提高雷诺数,使之与飞行雷诺数接近。风洞的雷诺数越接近真实飞行器的雷诺数,则从模型采集的空气动力学数据对于预测飞行器的飞行性能就越准确。

能量比是实验段气流的动能流率,即单位时间通过的动能与通过动力系统输入风洞的功率之比。它反映风洞的能源利用效率,能量比的数值越高,表明风洞的效率越高。

扰流度和天秤涉及风洞的工作精度。前者表征流体的流动性,扰流度越小,表示流体的流动越稳定、均匀;后者关系到模型空气动力学数据的读取精度,主要体现在天秤的感量上,感量越小,测量越精确。

前人的研究存在三个问题：(1)对雷诺数存在误读;(2)对能量比未予足够重视;(3)对扰流度和天秤精度缺乏进一步的分析。这些状况影响到对这座风洞的精准认识。

2 雷诺数：误读与再解读

风洞的雷诺数决定于实验段口径尺寸、气流速度和气体物性(3)主要是气体密度ρ和粘性系数μ两项参数。。对于清华风洞这样的常压风洞,在实验段口径确定、气体物性稳定的情况下,其雷诺数最高值决定于最大气流速度。然而学界对清华风洞的最大气流速度说法不一,进而导致对最高雷诺数未能形成统一意见。

2.1 雷诺数的三个值

黄延复给出的数据是最大风速44.7米/秒(100英里/时或146.7英尺/秒(4)原文的有关数据采用了英制,本文改用通行的国际单位制。下同。),没有说明雷诺数值。[1]《建国前中国空气动力学的发展》说最高雷诺数为5.5×106,未讲明该值为何种情况下所得,还说风洞气流速度为22.4米/秒。[3]姜长英的说法是,风洞配备的发动机是52千瓦(70马力),风速可达53.6米/秒,雷诺数为5.5×106。[4]金富军、王向田的数据是风速53.6米/秒、雷诺数5.5×106,但缺发动机功率数据。[6]

分析以往各家数据,不难发现,清华风洞的最大气流速度存在3个值,分别为53.6米/秒、44.7米/秒、22.4米/秒,那么相应的最高雷诺数当是3个值,除了上面提到的5.5×106,其余两个值是多少,未见有人提及。

风洞设计者王士倬等人的重要论文《清华大学机械工程系之航空风洞》记载,设计风洞时推算所能达到的最高雷诺数为5.5×106,前提是如果配备了功率为95千瓦的发动机,此时气流速度为53.6米/秒。[8]而清华大学实际订购的发动机为德国造52千瓦电动机,当时估算风洞气流速度可达44.7米/秒[11],亦属理论推算。按照王士倬的公式(5)现在通行的雷诺数计算公式为Re=ρvL/μ,其中ρ是流体密度,v是速度,L是特征长度(例如风洞实验段直径),μ是流体的动力粘性系数。王士倬使用的公式为Re=vL/γ,用运动学粘性系数γ代替了通行公式中动力粘性系数与密度的比值,即γ=μ/ρ,并在计算时使用了英制单位,其中v=176英尺/秒,L=5英尺,γ=0.000 159英尺2/秒(王士倬引自 Warner著1927年版Airplane design,但未指明温度条件,合0.000 014 7米2/秒)。如果用现代通行的雷诺数公式,在一个标准大气压、20℃条件下,取ρ=1.141kg·m-3、μ=17.9×10-6Pa·s(此时γ=μ/ρ=0.000 015 7米2/秒),则计算得到3个风速对应的雷诺数分别为5.2×106、4.3×106、3.5×106,稍低于王士倬计算值,系相关系数取值条件不同所致。可算得此时雷诺数为4.6×106。德制电动机“1936年2月初运到校内之后,适逢日本武力威胁北京,时局震摇,随校中图书仪器,一同装车,设法运往汉口保藏”,乃至风洞“缺电动机,只好收罗旧卡车发动机代替”。[2]汽车的品牌是别克(Buick)[9],发动机型号不详,但其功率很可能较小(6)该发动机的功率,目前所见资料均无记载,可从风洞实际最大风速22.4米/秒推知为41千瓦。,以致风洞动力不足,运行时的实际最大风速小于原设计值,仅为22.4米/秒。[2]

据上述情况,通过王士倬所用雷诺数计算公式对以上风速稍加计算,便可得知风洞存在3个动力、气流速度及雷诺数组合：(1)95千瓦、53.6米/秒、5.5×106;(2)52千瓦、44.7米/秒、4.6×106;(3)41千瓦、22.4米/秒、3.7×106。第1、2组的雷诺数均是推算,第3组的雷诺数是当时实际运行时的数值。即清华风洞实际配备的动力仅有41千瓦,风洞的最大气流速度为22.4米/秒,此时的最高雷诺数只有3.7×106。当然也不能认定风洞设计的雷诺数只有3.7×106,由于风洞设计和运行都非常成功,而订购的发动机为52千瓦电动机,如安装这一电动机,应当可以达到4.6×106。但这与以往认为的雷诺数5.5×106仍有一定差距。以往相关研究多未能区分清华风洞雷诺数的理论计算值与实际达到值,造成误读。

以上仅从风速出发讨论了清华风洞的雷诺数,实际上雷诺数涉及的因素不止于此。温度也有很大影响,温度越高空气粘性系数越大,从而雷诺数会相应减小。现在研制的高雷诺数风洞,往往通过液氮冷却,使之在低温下运行,从而实现高雷诺数。清华风洞没有配备此类冷却系统,当风洞运行时,洞内空气因摩擦而升温,雷诺数会有所降低。此外,粘性系数还与风洞实验段的尺寸与光滑度有关,风洞口径越小、内壁越粗糙,对提高雷诺数越不利。因此,考虑到这些因素,清华风洞的实际雷诺数恐怕要比3.7×106还要低些,特别是在长时间连续运行后。

2.2 与外国风洞的比较

清华风洞的雷诺数究竟是高还是低,与同时代的世界同类风洞比照,较易做出判断。表1列出了一些国家代表性风洞及其核心参数值。表中风洞包括两类,正常气压小口径风洞、常压大口径风洞。清华风洞属于常压小口径风洞。剔除大口径风洞,限定在小口径类风洞中讨论。

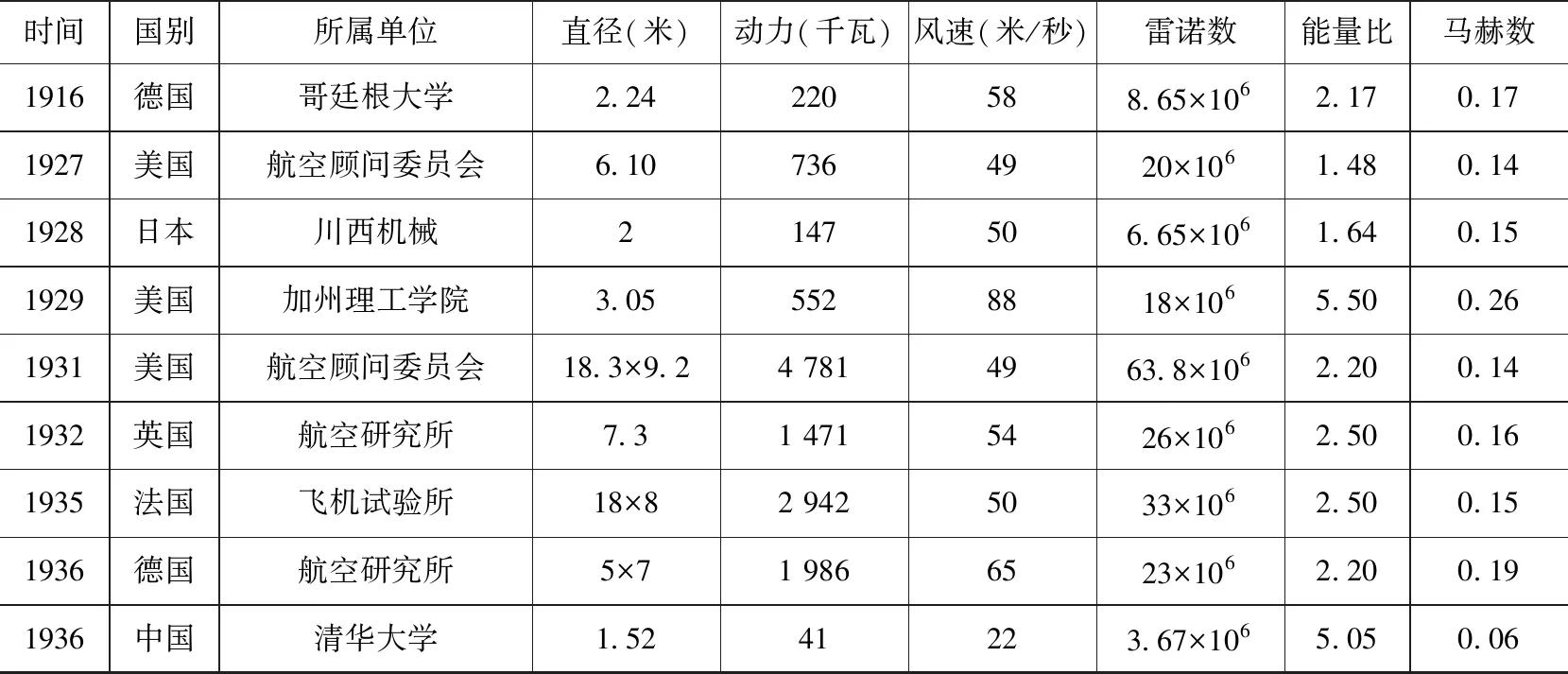
表1 清华风洞与截至1936年世界代表性风洞主要实测数据对比1)

口径与清华风洞接近的有1916年建成的德国2.24米风洞和1928年的日本2米风洞。3座风洞在雷诺数上,不存在数量级的差别。从这项关键参数看,清华风洞的技术水平,整体上相当于德国1916年或日本1928年的水平。但清华风洞的能量比极为优秀,仅次于美国加州理工学院1929年建成的3.05米风洞。

衡量风洞技术的关键参数,除雷诺数外还有马赫数(Mach number)(7)以奥地利物理学家恩斯特·马赫(Ernst Mach,1838—1916)的姓命名,简称M数。,它们均与气流速度有关。马赫数是指气流速度与音速之比,其物理意义在于表示了物体所受空气的惯性力与弹性力之比。弹性力反映了空气的压缩性,所以马赫数也体现了压缩性的影响。作为一项关键参数,马赫数常被用以对风洞进行分类。马赫数小于0.3的风洞称为低速风洞;马赫数在0.3—0.8范围内的风洞为亚音速风洞;马赫数在0.8—1.2范围内为跨音速风洞;马赫数在1.2—5.0范围内为超音速风洞;马赫数大于5.0的风洞为高超音速风洞。

风洞实验是利用相似性原理,通过模型来模拟实际飞行,要求实验流场与飞行器实际飞行的流场之间遵循多个相似性准则,其中雷诺数与马赫数是极其重要的两项。如果撇开马赫数,仅仅基于雷诺数的比较来评价清华风洞与同时代类似规模风洞的技术水平是否可行?

实际上,风洞实验不能同时满足相似律所提出的所有相似准则。在不同速度范围内或类型的实验中,主要相似准则是不同的。在低速范围内,气流是不可压缩流,马赫数影响很小,可以忽略不计,主要的相似准则是表征空气粘性影响的雷诺数。而超过音速时,气流是可压缩流,马赫数对物体的气动影响非常明显,为了保持实验流场与实际流场之间的相似性,必须满足的相似准则是马赫数相似。即在低速范围内主要考虑雷诺数,而在超过音速时则以关注马赫数为主。[12]

表1所涉风洞的马赫数均未超过0.3,俱属低速风洞。在这一前提下,占主导地位的是雷诺数相似准则。故通过雷诺数的比较来衡量同类风洞的技术水准,具有相当参考价值。清华风洞所处的时代,尽管超音速风洞已经出现,但低速风洞是主流,当时风洞技术的改进也是围绕如何提高雷诺数推进的。学术界以往在研究清华风洞的关键参数时聚焦于雷诺数而忽略马赫数,原因盖在于此。

3 能量比：优先级与风洞设计者的理念

以往的研究,尽管也提到清华风洞的能量比[2,4,6],但局限于强调其具有较高数值,并未深入分析。事实上,能量比这项参数对于清华风洞有特殊重要的意义,需要重新加以审视。

风洞的雷诺数、能量比、扰流度及天秤感量等参数在风洞设计时的排序,反映了风洞设计者的设计理念。当时国外风洞设计师最优先考虑雷诺数,而王士倬的设计首重能量比。“查清华风洞中费用最大之一项,即为电气马达,亦即其中唯一之外国制造品,既掷重资以购原动力,自必须尽力使效率增高,其它皆属次要”,“尤其注意能量比与雷诺数”。[8]风洞建造完成后,经实测能量比达到5.05[10],该值仅次于加州理工学院风洞的5.5[8],完美地实现了当初的设计意图。将能量比置于风洞设计的最优先考虑位置,体现了王士倬效率优先的设计理念,契合当时国情。

王士倬将能量比较高的加州理工学院风洞作为参考对象。该风洞“为冯·卡门所设计,乃由普朗特式改良,堪称当代最经济之建筑,清华风洞,大致仿该式设计”[8]。有关档案记载,在设计风洞之初,清华大学曾经“分别致函美国麻省理工大学及加州理工学院航空工程系,索取各种风洞图样”。[13]

根据考虑能量比、效率优先的总设计理念,结合建成后的用途,确定了风洞的规模与构型。小型风洞主要用于基础研究和先进气动技术探索;中型风洞用于中小型飞行器选型、校核和定型实验;大型风洞用于大型飞行器的选型、校核和定型实验等。风洞越大越有利于增大雷诺数。但风洞尺寸越大,建设难度越大、运行成本越高,必须找到模拟准确度、可行性与经济性等几个因素的最佳结合点,合理确定风洞尺寸。清华在筹建风洞之初,经过综合考虑,决定建造用于科研的小型风洞。先是计划建造实验段口径1.22米、总长度30.5米的风洞[14],后改为口径1.52米、长度15.24米[15]。至于风洞的构型,当时可选维纳姆发明的直流式,这是个两端开口的木箱,气流从一端进入,在另一端排出;也可选德国人普朗特(Ludwig Prandtl,1875—1953)1908年创制的回流式。回流式优于直流式的地方是：在发动机功率相同时,气流的速度更高、均匀性更好,且雷诺数和能量比更高些。当时直流式风洞只被法国等少数国家采用,回流式为多数国家所采用。清华风洞亦选用较为优越的回流式构型。

4 扰流度与天秤感量：高精度与风洞设计的新探索

清华风洞的扰流度和天秤感量两项参数的指标在当时颇为优异。研究人员通过这座风洞进行空气动力学相关研究,发表了中国最早的几篇航空研究论文。该风洞的建造和应用为中国早期风洞技术的进步做出了重要贡献。学界对其达到的精度多有赞誉,但对其作用和影响却探讨不足。

清华风洞的扰流度是1%,“能量比良好,流动条件令人满意,湍流适中,用典型机翼剖面模型所得实验结果,可与其他类似雷诺数的风洞相媲美”。[9]“与德国哥廷根2.2米风洞及美国加省理工学院3米风洞比较,颇为符合。”[16]清华风洞的天秤可测量阻力、升力及扭力等6个分力,感量为0.25克。[17]冯桂连测试了R.A.F15薄型翼、克拉克Y中厚度翼以及哥廷根387高厚度翼3种典型机翼模型,其结果与世界同类风洞所测结果相符合。[17]冯·卡门说“没想到,中国能建造如此精确的风洞,已经达到国际水平”。[7]

得益于风洞的高精度,科研人员做出了很有意义的发现,为更高水平风洞的设计做了十分有益的探索。一是发现雷诺数达到一定数值时,大直径风洞所需的发动机功率更少[18],这就为较大型风洞装配较小的发动机提供了理论依据,对节省建设资金有利。二是发现风洞扩散段扩散角在6°附近时能量损失最小[18],此点对风洞结构的设计具有指导意义。这些成就为深入了解回流式风洞的内在规律奠定了基础,也为高能量比风洞的设计建立了理论基础。清华1936年设计的南昌4.5米大型风洞和浙江大学1949年设计的0.9米风洞就应用了这些成果。[19]清华风洞对中国航空学术的早期发展发挥了重要而独特的作用,是一座奠基性风洞。

5 余论：是自制还是仿制?

以上解读与分析,对清华风洞有了更为深刻全面的认识。不过还有一个重要问题需要做出定论,即风洞的研制方式问题。

一种意见认为清华风洞是仿制[4],另一种则认为是自制[6]。即使参加研制的当事人,在这一问题上的看法也不完全一致。王士倬的助手张捷迁(1908—2004) 在回忆文章中谈到风洞建造时说：“自制实验风洞,主张谨慎进展。首先仿造外国著名风洞数种,制作模型,实验性能,研究制造上的难处”[2]。他认为先仿制了模型风洞,在此基础上自制清华风洞。而根据王士倬“大致仿该式设计”的说法,清华风洞似为仿制。

应当说当事人的说法都有道理,关键是如何界定“仿制”和“自制”。一般情况下,仿制是测绘仿制,对已有成品进行测绘获得图纸,通过摸索,搞清楚原理和制作工艺,然后制造出性能相同或接近的产品。清华风洞显然不属于这种仿制。自制一般是指自主研发。其中,高水平的自制,从概念设计到原型设计、再到试生产全部依托自身力量,属于原创性很高的自主研发,是自主创新。清华的风洞研制,应该还不是这一层次的自制。

称清华风洞为自制或自主研发也是合适的。清华的设计只是参考了加州理工学院风洞的设计思想,从设计到选材和制造全程都是依靠自己力量完成的。“除用以转动螺旋桨之电气马达系购自外国外,其余一切,均由该校自行设计制造,即所用之自动平衡式天秤五具,亦由该校工厂自制”[8],而设计目标和方案显然与加州理工学院风洞不同。突出特点是根据国情对风洞参数的优先级做了调整,考虑了实际需要和材料、成本等多种因素,并先研制了小的模型风洞进行测试,然后才制造了研究用实验风洞。从这些事实看,清华风洞的研制属于自主研发范畴。王士倬称“大致仿该式设计”,应当指的是参考了加州理工学院风洞的方案,并非是通常意义下对该风洞的仿制。因此,清华大学研制的风洞无疑是一座自制风洞。