剪下最大的图形

◎相 辉

数学活动课上，高老师给同学们出了一道题目：

例题

在一个长是20厘米，宽是8厘米的长方形中，剪下一个最大的正方形，求正方形的面积。如果剪下一个最大的三角形，三角形的底和高分别是多少？面积是多少呢？

机灵的周米多马上站起来说：“要想使正方形的面积最大，肯定要使正方形的边长达到最大数值。长方形最长的边是20 厘米，所以正方形的面积是20×20=400（平方厘米）。同样，要使剪下的三角形面积最大，底和高也要达到最大数值，所以三角形的面积是20×20÷2=200（平方厘米）。”

爱思考的乔璞瑞举手发言道：“周米多同学想得不对。我们可以联系实际动手剪一剪。20 厘米长的长方形不可能剪出边长是20 厘米的正方形。在长方形里剪最大的正方形时，正方形的边长只能和长方形的宽一样长，而不能和长方形的长一样长。所以，在这个长方形中剪下的正方形的最大面积是8×8=64（平方厘米）。同样，要剪出一个最大的三角形，三角形的底和高只能是长方形的长和宽，因此这个三角形的最大面积是20×8×=80（平方厘米）。”

同学们都赞同乔璞瑞同学的想法，高老师也投来了赞许的目光。随后，高老师又给同学们出了一道题目：

在一个梯形中剪下一个最大的长方形，求长方形的周长。如果剪下一个最大的三角形，三角形的底和高分别是多少？

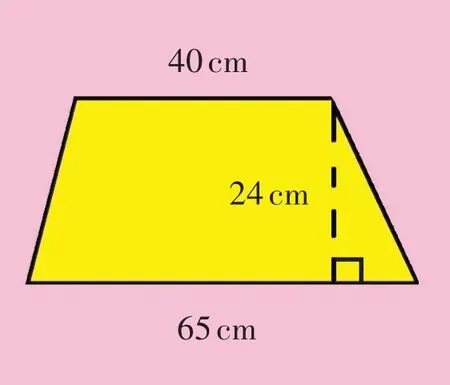
不一会儿，高朗同学发言说：“在这个梯形中剪下一个最大的长方形，长方形的长只能是上底40厘米，不可能是下底65厘米，宽是梯形的高24厘米，因此长方形的周长是（40+24）×2=128（厘米）。要想剪下一个最大的三角形，要用梯形的下底作为三角形的底，梯形的高作为三角形的高。所以剪下的三角形的底是65厘米，高是24厘米。”

同学们一致同意高朗同学的想法，同时也体会到：解决此类问题时，既要考虑图形的特征，还要联系实际，亲自动手实践来验证猜想是否正确。

最后高老师问道：“如果在这个梯形里剪下一个最大的正方形，它的边长应该是多少呢？请大家再想一想。”