考虑负荷时序特性的居民柔性资源低碳协同方法
熊伟笑,高 辉,陈 璐,杨凤坤
(1.南京邮电大学 自动化、人工智能学院,南京 210003;2.国电南瑞科技股份有限公司,南京 210016)
0 引言
据统计,电力行业碳排放占全国总碳排放的四成以上[1],是实现“双碳”目标的关键。从表面上看,发电企业是二氧化碳的直接排放者[2],但电力系统“源随荷动”特征表明用户侧才是全网碳排主要责任人[3],实现用户侧用能低碳性具有重要意义。文献[4]以碳排放因子为引导信号,提出了一种引导用户侧主动响应并降低系统碳排放的低碳需求响应机制,并建立相应的减碳效益分析模型,验证用户侧低碳需求响应机制具有较大的减碳潜力。文献[5]引入奖惩阶梯型碳交易机制,建立了一种计及氢能利用和需求响应的综合能源系统低碳优化调度模型。文献[6]建立了电-热综合区域能源系统下的低碳经济调度模型,利用需求侧响应对用电负荷进行针对性优化,以降低系统负荷的峰谷差水平。
目前,我国居民家电保有量已达到较高水平,导致居民用电量飞速增长[7]。居民家电负荷具有响应资源多样[8]、可控性强[9]、聚合潜力大[10]等特点。针对居民柔性资源协同优化问题的研究主要涉及削峰填谷[11-12]、节能降耗[13]、用电经济性[14-15]等方面。文献[11]将家电设备按负荷特性分为开关型、分档型和连续型,考虑负载方差建立相应负荷调度模型,并采用改进粒子群算法进行求解;文献[12]提出了居民用户参与电网调峰的调控机制,在最小化用电成本时考虑了居民用户的调峰潜力;文献[13]从居民负荷与系统负荷相关性出发,提出了反映居民用电对电网调峰贡献度的调峰激励机制,并综合考虑用电成本、舒适度和调峰激励建立居民用户用电优化策略。文献[14]基于非侵入式负荷监测算法,对家电设备用电信息进行实时监测,以用电成本和舒适度为目标建立家庭用能管理优化调度模型;文献[15]将家用电器分为可平移负荷、可中断负荷、HVAC设备3类,并通过功效系数法建立基于经济性和舒适度的多目标优化模型。上述研究侧重于以经济性为目标的需求响应,且大多采用物理建模、数据驱动等传统分析方法提取居民用电行为特征,难以准确发掘居民用电行为的时序特征,造成居民响应潜力无法匹配等问题。
进一步地,文献[16-18]开展了居民低碳需求响应研究,提出以平均碳排放因子来核算碳排放量的居民低碳需求响应模型,并以碳市场中用户收益最大以及电力系统运行成本最小为目标,提出一种基于碳价的低碳需求响应方法,但是并未考虑碳排放因子的实时特性。随着新能源占比不断增加,且新能源随机性与波动性等特征使得不同时段发电机机组组成显著不同,用户侧等效碳排放差异明显变大,平均碳排放因子无法衡量这种差异。因此,在居民柔性资源低碳协同方法引入实时碳排放因子计量具有重要意义。
基于上述背景,本文充分考虑居民负荷的时序特性,提出了基于贝叶斯网络构造居民柔性资源用能概率模型,实现居民家电负荷舒适度精准建模;并引入实时碳排放因子,提出考虑负荷时序特性的居民柔性资源低碳协同方法。
1 需求响应特性下居民柔性资源类型划分
家电设备按功率是否可调分为恒功率设备和可调功率设备;按其运行特性分为可转移设备和可中断设备;按其储能特性分为储能设备和非储能设备。如照明及娱乐类设备,需求时间固定,一般需保持稳定运行,无功率可调、可转移、可中断及储能特性,称为固定负荷;如洗衣机、洗碗机等设备,运行时间可以平移,但开启后必须连续运行至工作结束,称为可平移负荷;如热水器、空调等设备,工作过程中可以中断运行,负荷高峰时期可通过中断负荷来削减用电量,称为可中断负荷;如电动汽车及电池类设备,充放电过程中可调节功率大小,且具备可转移、可中断、储能特性,称为储能设备。3类负荷典型实例如表1所示。
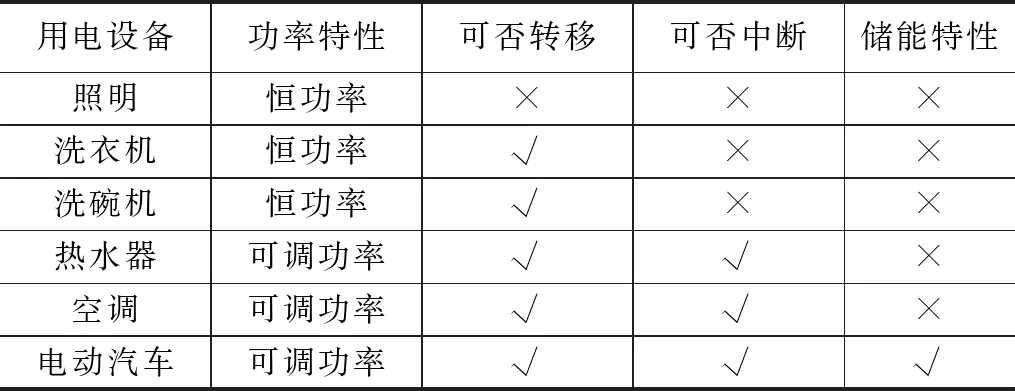
表1 典型设备及其负荷特性示例
以一天(0:00-24:00)为调度周期进行家居设备用电优化,将一天分为24个时段,各时段时长为Δt=1,t∈[1,2,3,…,24];家电设备集合用A表示,对于任意属于A的家电负荷a,其运行功率情况Pa={Pa,1,Pa,2,…,Pa,24};引入0~1辅助变量sa,t表示设备a的工作状态,1为开启状态,0为关闭状态;居民用户t时段用电需求为:
(1)
2 基于贝叶斯网络的负荷用电概率建模
针对居民负荷用电行为影响因素众多、不确定性大等问题,为进一步分析居民用电行为的时序特征,实现家电负荷用电舒适度精准建模,本文提出了一种基于贝叶斯网络的居民负荷用电概率分析方法。
2.1 基于贝叶斯网络的负荷时序状态分析
贝叶斯网络基于贝叶斯公式,将概率论与图论相关知识联系起来,通过观测先验知识与样本数据来获取预测变量的概率信息,能够表征变量间复杂不确定性关系、挖掘数据间潜在关联[19]。本文结合居民用电行为与外部数据相关等特点,从居民负荷的时间序列特性出发,充分考虑用户用电意愿及行为习惯,基于贝叶斯网络构建负荷用电的时序状态分析模型。
以环境温度、日期类型、负荷历史用电数据及设备开启状态为节点变量,构建网络拓扑结构如图1所示。为便于分析,对环境温度、日期类型、负荷历史用电数据及用电设备开启状态属性范围进行划分。
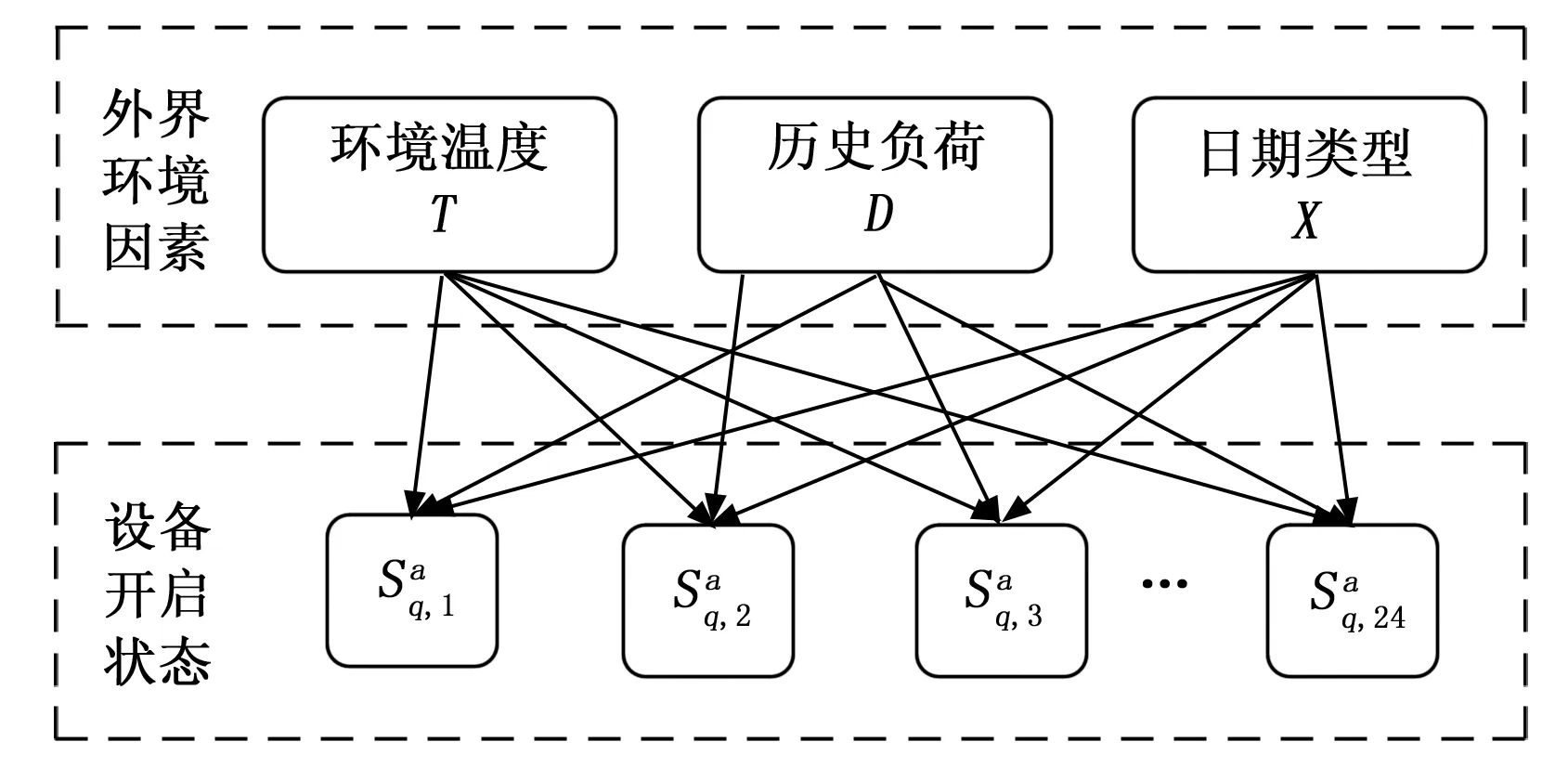
图1 负荷时序状态分析贝叶斯网络模型
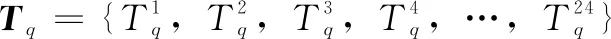
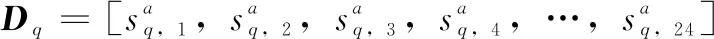
(2)
(3)

X={1,2,3,4,5,6,7,8}:1~7表示周一到周日七天,8表示节假日。
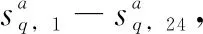
(4)
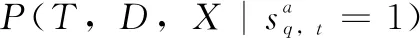
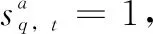
(5)
根据式(4)~(5)可求出家电设备a在一天中各时段的用电概率。构建各类设备的负荷时序状态分析模型,可得负荷的用电状态概率矩阵p,矩阵元素由负荷各时段用电概率构成。基于此,分析各时段内各设备的用电可能性大小。
(6)
式中,pm,t为第m种用电负荷t时段的用电概率,pm,t越大说明居民在该时段使用该负荷的意愿越强,参与调控的意愿越小。
2.2 基于用电概率的舒适度建模
居民柔性负荷用电舒适度体现在调度前后居民家电使用习惯的改变;以家电设备使用概率最高点为最佳运行点,定义居民负荷用电时段用电概率偏离最佳运行点用电概率的程度为柔性设备a运行在时段t时用户对其的舒适性:
(7)
(8)
式中,pa,max为用电设备a在各时段用电概率中的最大值;pa,min为用电设备a在各时段用电概率中的最小值;ωa为权重系数,即负荷a用电行为对居民用户影响程度;Ca值越大表明优化方案对用户使用习惯改变越小,用户对该用电设备用电满意度越高。
3 居民柔性资源低碳协同优化模型
3.1 实时碳排放因子
考虑到不同时段能源供给侧发电机机组组成成分存在差异,居民用户不同时段用电行为对应发电侧产生的碳排放显著不同[20]。传统采用平均碳排放因子的电力碳计量方法无法表征不同时段多类型发电机机组不同占比带来的差别。同时,考虑清洁能源就地消纳对区域电网碳排放因子的影响,提出实时碳排放因子的计算方法。
(9)
ej,t=εj,t·(1-βj,t)
(10)
式中,εj,t为区域电网j时段t单位购电碳排放计量因子;h∈[1,2,…,H]表征各种发电机机组类型;αh,t为各类型发电机机组发电量占比;eh,t为h类发电机机组时段t单位发电碳排放因子;ej,t为区域电网j时段t的实时碳排放因子;βj,t为区域电网j时段t的清洁能源发电占比;αh,t、βj,t均由电网日前调度数据获得。
3.2 优化模型
用户参与需求响应主要是调整家庭内各设备的用电时间,达成降低用电成本的目的。目标函数如式(11)所示:
(11)

在“双碳”目标推动下,利用用户侧低碳需求响应减少碳排放备受关注,碳减排也应纳入居民柔性资源协同优化的目标函数中,为开展低碳居民柔性资源协同优化方法设计提供新思路。用户单日碳排量最低如式(12)所示:
(12)
为同时兼顾经济性和低碳性,采用加权方式构建目标,如式(13)所示:
minF=α1Ccost+α2CCO2
(13)
α1+α2=1
(14)
式中,α1、α2为每个子目标的权重因子。
3.3 约束条件
3.3.1 功率平衡约束
居民侧负荷消耗的电能由电网和分布式电源发电供应,应时刻满足功率平衡约束:
(15)
3.3.2 用户用电舒适度约束
需求响应行为对居民用电舒适度产生不利影响,应保证用户用电舒适度大于等于某一阈值[21],如下:
Ctotal≥Cset
(16)
式中,Cset为用户用电舒适度设定值,由用户根据自身用电习惯设定。
3.4 求解流程
考虑负荷时序特性的居民柔性资源低碳协同优化模型包括用电成本、碳排放量两个目标函数,采用粒子群算法对模型进行求解。电器在某个时段是否开启是模型的决策变量。设置最大迭代次数为Nmax,当前迭代为t,粒子种群规模为S,每个粒子维度为(m+n),具体求解步骤如下所示。
步骤1:输入实时电价、实时碳排放因子、居民侧负荷运行参数、舒适度等参数。
步骤2:初始化粒子群参数,包括种群规模、粒子维度、最大迭代次数、惯性权重、学习因子;
步骤3:初始化每个粒子的位置和速度,令迭代次数t=1;
步骤4:计算优化函数的初始适应度值F,得出个体最优值pbi=(pi1,pi2,…,piD)与全局最优值gbi=(gi1,gi2,…,giD);
步骤5:根据式(29)~(30)更新粒子j的速度和位置[22];
(17)
(18)
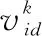
步骤6:计算个体适应值F,更新个体与全局最优值,更新迭代次数等参数;
步骤7:判断是否满足终止条件,若当前迭代次数达到Nmax则输出最优方案,否则重复步骤5~7。
4 算例分析
4.1 基础数据
本文选取洗衣机、洗碗机、空调、热水器、电动汽车设备作为可调度柔性设备进行优化运行仿真实验。为方便仿真,对用电设备进行较为理想化的假设和简化,设备运行时均以额定功率运行且每个时段保持连续运行,采用文献[17]中的用电设备数据,如表2所示。调度周期从00:00—24:00,仿真步长Δt=1 h。
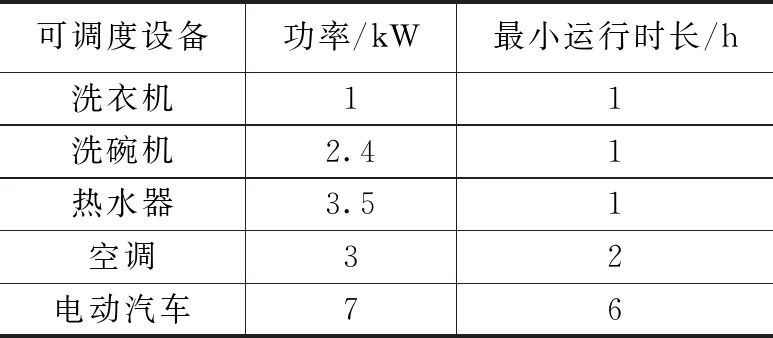
表2 可调度设备基本信息
4.2 负荷时段挖掘结果分析
选取预测日前150天洗衣机、洗碗机、空调、热水器、电动汽车历史负荷数据作为训练样本集,基于负荷用电时段挖掘方法预测第151天的使用情况。表3显示了洗衣机、洗碗机、空调、热水器、电动汽车一天中不同时段的用电行为概率。
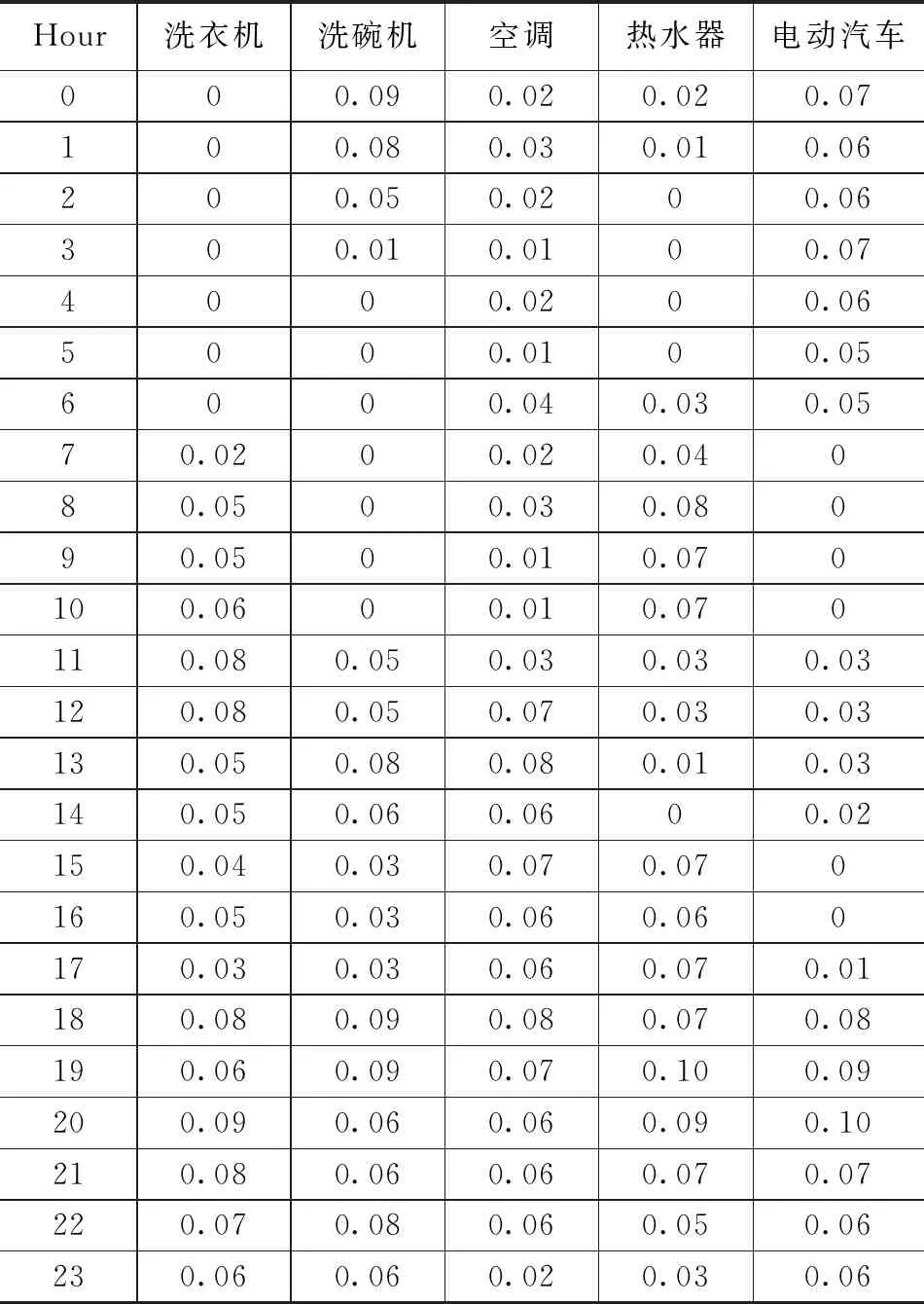
表3 用电状态概率矩阵
表3给出了5种负荷的用电状态概率矩阵,通过分析可以发现,洗衣机使用行为集中分布在早上7:00到晚上23:00之间;洗碗机的时段属性也较为明显,在中午11:00至次日凌晨时段运行较为频繁;空调负荷在全天内都有使用行为发生;热水器使用行为的发生时间主要集中在08:00-10:00与15:00-23:00,其他时段的使用行为较少;电动汽车使用的最高概率分布在晚上18:00之后至次日凌晨时间段。
4.3 优化结果分析
为验证本文协同优化方法的有效性,以式(12)为目标函数,设定权重因子α1=0.3,α1=0.7进行优化仿真,各时段实时碳排放因子计算结果参考文献[4],光伏电源出力数据参考文献[23],实时电价数据参考文献[24],设置粒子群种群规模S=200,惯性权重ω=0.718,学习因子c1=c2=1.510,最大迭代次数Nmax=200,舒适度参数Cset=0.6,未优化前各家庭用电设备运行时段如图2所示。

图2 响应前家庭用电设备运行图
图3展示了该用户参与响应前后的负荷变化情况。经优化后各用电设备运行时段如图4所示。

图3 响应前后用户用电行为对比

图4 响应后家庭用电设备运行图
由表4可以看出,居民参与响应后的碳排放量相较于响应前降低了22.6%,在实时碳排放因子的引导下,该优化方法起到了明显的碳减排效果;同时,响应后的用电费用相较于响应前降低了11.9%,经济性和低碳性都达到了较高的效果,且响应后负荷曲线峰谷差降低了21.4%,均方差减少了11.8%,有效降低了负荷波动。从结果分析来看,利用考虑负荷时序特性的居民柔性资源低碳协同优化模型,可在降低用户用电费用的同时,有效地提升低碳性,降低二氧化碳的排放量。

表4 响应前后数据对比
4.4 场景对比分析
为验证考虑负荷时序特性的居民柔性资源低碳协同优化模型的优势,设计以下几种场景进行对比分析。
场景1:以低碳性为目标进行优化仿真;
场景2:以经济性为目标进行优化仿真;
场景3:以低碳性和经济性为目标,并且设定权重因子α1=0.3、α2=0.7进行优化仿真。
3种场景下响应前后用户用电行为对比如图3、图5、图6所示,响应结果对比如表5所示。
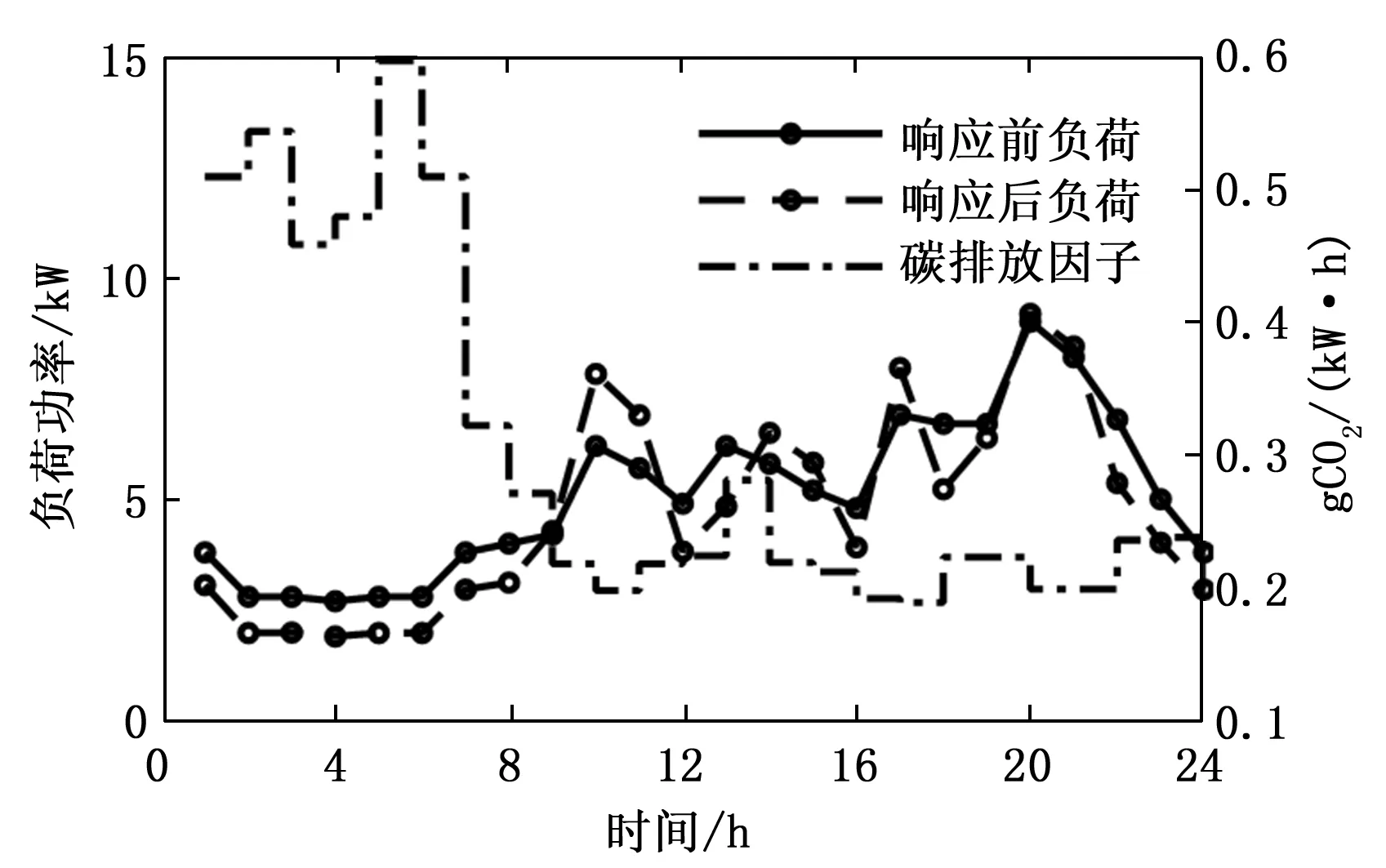
图5 场景1响应前后用户用电行为对比

图6 场景2响应前后用户用电行为对比
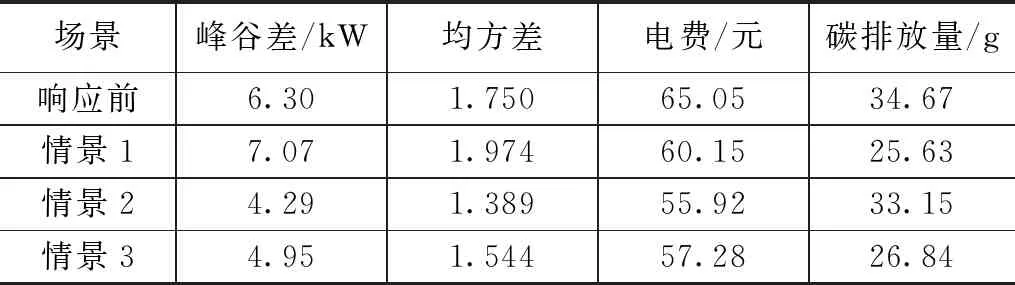
表5 响应前后用电负荷数据对比
由表5可以看出,情景1中,居民参与低碳需求响应后的碳排放量相较于响应前降低了26.07%,在实时碳排放因子的引导下,该低碳需求响应策略起到了明显的碳减排效果;同时,响应后的用电费用相较于响应前降低了7.5%,此处用电费用降低主要有两个原因:一是以低碳性为目的的优化调度关闭了部分可中断家庭柔性负荷的使用,使用电量降低,从而降低了用电费用;二是分布式电源在11:00-16:00时出力较大,用户在该时段使用分布式能源抵消部分电器功率消耗,使耗电量曲线明显降低,用电费用也随之下降。但是,居民参与响应后的负荷曲线相较于响应前的曲线峰谷差增加12.2%,均方差增加12.8%,低碳需求响应策略使谷时负荷水平变得更低,同时也没有降低峰时负荷水平,造成峰谷差进一步加大,负荷曲线抖动更加严重,并不符合期望的用电曲线变化趋势。
情景2中,参与响应后相较于响应前的峰谷差降低了31.9%,均方差减少了20.63%,在实时电价激励下,高峰时段的用电量明显减少,该响应策略起到了明显的调峰效果。同时,响应后的用电费用相较于响应前减少了14.04%,用电成本节约效果较为显著;碳排放量相较于响应前减少了4.4%,此处碳排放量减少原因与情景1中用电费用降低原因相同,且碳减排效果明显低于情景1。
由以上分析结果可知,若只考虑碳排放最小时,低碳性达到最优,经济性最低,且此时优化后负荷曲线的峰谷差、均方差均高于优化前,不符合期望的用电曲线变化趋势;若只考虑用电费用最小时,经济性达到最高,优化后负荷曲线峰谷差、均方差最小,但是低碳性优化结果明显低于单一低碳性的优化。
从表5还可以看出,情景3中,参与响应后相较于响应前用电费用降低了11.9%,碳排放量减少了22.6%,经济性和低碳性都达到了较高的效果,且响应后负荷曲线峰谷差降低了21.4%,均方差减少了11.8%,有效降低了负荷波动。
在构建考虑负荷时序特性的居民柔性资源低碳协同优化模型时,目标兼顾低碳和经济需求,可在降低用电成本的同时,同步降低用户的用电碳排放量,实现经济性、低碳性多目标趋优。
5 结束语
本文针对居民用电时段不确定性特点,提出了基于贝叶斯网络构造居民柔性资源用能概率模型,通过模糊聚类的方法挖掘柔性资源使用时段,实现居民家电负荷精准建模;并在此基础上引入实时碳计量模型,基于实时电价,提出了一种考虑用电经济性和低碳性的居民柔性资源低碳协同优化方法,得到以下结论:
1)先基于贝叶斯网络构建居民负荷用能概率模型,挖掘出居民用电时序特征,再参与需求响应,可保证用户参与需求响应过程中,不会违背用户自身消费偏好。
2)本文所构建的居民柔性资源低碳协同优化模型,在降低居民用户用电成本的同时,同步降低了用户的用电碳排放量,且相对于单一经济性目标,该模型减碳作用更加明显;相对于单一低碳性目标,该模型有效降低了负荷峰谷差,对系统的负荷波动起到了较好的平抑作用。
所提模型并未考虑用户在低碳需求响应中如何获取经济收益,碳减排量如何与居民用户收益协同问题是下一步研究方向。

