预警机制的鲸鱼算法及时间约束的航迹规划

闫浩泉，杨柳庆，张 勇

(1.南京航空航天大学 自动化学院，南京 211106；2.南京航空航天大学 无人机研究院，南京 211106；3.南京航空航天大学 中小型无人机先进技术工业和信息化部重点实验室，南京 211106)

0 引言

无人机技术的高速发展使其在石油、军事、农业、气象、地理测绘等领域展现广泛的应用潜力。不同于四旋翼无人机，军用固定翼无人机的发展越来越重视对控制系统的实时性设计。无论是无人机蜂群技术的小型化发展趋势[1]，还是高超声速无人机的超高速发展趋势[2]，短距离与长续航均对航迹规划的求解提出了快速性要求。

无人机航迹规划是典型的多目标优化问题。旨在综合考虑环境威胁、战场威胁、飞行时间、油耗等多约束条件下，寻找一条从起始点到目标点的最优或可行的飞行轨迹。目前的优化求解算法可大致分为两类，传统优化算法与智能优化算法。基于图论的Voronoi图法[3]、基于随机抽样的随机搜索树算法RRT[4]，动态规划等均属于传统优化算法。此类算法提出时间早，理论成熟，但在解决凸优化等日益复杂的优化问题表现乏力。新型智能优化算法包括不限于各类群智能优化算法：蚁群算法(ACO，ant colony optimization)[5]、粒子群算法(PSO，particle swarm optimization)[6]、灰狼算法(GWO，grey wolf optimizer)[7]、鲸鱼优化算法(WOA，whale optimization algorithm)[8]等。各类机器学习算法：Q学习算法[9]、深度确定性策略梯度算法(DDPG，deep deterministic policy gradient)[10]等。多数群智能算法是通过观察自然界中的生物群体并分析对应的群体智能性发展而来的仿生算法。个体的数量决定并行运算的规模，个体之间的信息交流决定并行运算的效率。算法具备收敛性前提下，二者合力影响求解的效率。鲸鱼优化算法相比ACO算法与PSO算法，参数少，信息交流机制丰富，具有、易于实现、高效、普适性等特点。即便对比于新兴的机器学习算法，也具有无训练时间成本、应用成熟的优势。

WOA算法[11]的生物模拟对象是捕食过程中的座头鲸群。已有众多学者通过对算法的自身改进以及算法的融合改进完成性能优化。算法的初始化方式以及随机机制是改进的常选对象，张永、王坚浩分别采用不同的混沌映射改善初始化方式、Zhang、liu等通过变异算子[12]以及莱维飞行扰动改进随机机制[13]，提高算法的探索能力。通过对自身种群进行分组还可以实现结构层面的改进。文献[14]将种群分成搜索组与猎物组，利用搜索组的最优个体引导猎物组。Kaveh提出的与碰撞优化算法混合的改进方法具有相似的机制[15]。刘小龙[16]将种群划分为多个相互独立的子群，使用横向和纵向两种对比方式影响个体。

融合改进则是融合其他群智能优化算法原理进行结构、随机机制优化的方法。Korashy将GWO的领导层结构引入WOA中，实现结构分级的优化[17]，Strumberger等人则将人工蜂群算法的搜索结构代替原有搜索机制[18]，提高种群丰富度。

针对WOA算法高维优化问题收敛速度慢，多极值问题易于早熟、陷入局部极值的问题，且为满足航迹规划的实时性要求，本文提出基于预警机制的鲸鱼优化算法(APWOA，adaptive probabilistic whale optimization algorithm)用于优化求解。同时将算法解算时间计入航迹代价的优化模型，提高实时性的优先级。APWOA算法引入与个体适应度相关的自适应概率控制3种更新机制的选取，对适应度低的个体发出预警，提高其进行随机更新的概率。从整体层面提高算法个体的差异性。同时自适应概率还参与WOA特有的螺旋式更新机制的自适应权重定义，控制收缩范围实现机制层面的探索与开发的平衡。为验证算法的收敛能力，使用优化算法的基准测试函数作为工具，与多种算法进行对比分析。针对航迹规划问题，在联合坐标等分法基础上，通过控制步长实现变维度的航迹序列生成，完成不同规划维度方面的仿真对比。

1 场景与鲸鱼优化算法

1.1 规划场景设计

1.1.1 地形威胁

根据飞行环境和任务要求建立适当的规划空间是解决路径规划的前提。数字高程地图(DEM，digital elevation map)为指定投影平面上的空间水平间隔的高程值矩阵，本质是关于高程平面坐标(x，y)的连续函数，实际使用时作为一个有限的离散集。采用文献[19]提及的地形模型函数采集DEM所需高程数据，具体为：

(1)

其中：(x，y)为水平面的点坐标，z为坐标(x，y)相对应的高度。a，b，c，d，e，f为相关系数，改变相关系数以获得不同地形数据。

第k山峰对无人机造成的山峰威胁表示为：

(2)

其中：d为无人机至山峰k对称轴的距离；dmin为地形最小作用距离。H(k)为山峰k的高度Rt为山峰的最大延伸半径；Rt(h)的计算公式为：

Rt(h)=(H(k)-h)/tanθ

(3)

其中：θ为该山峰地形的坡度。

式(2)、式(3)中各变量间的关系如图1所示。

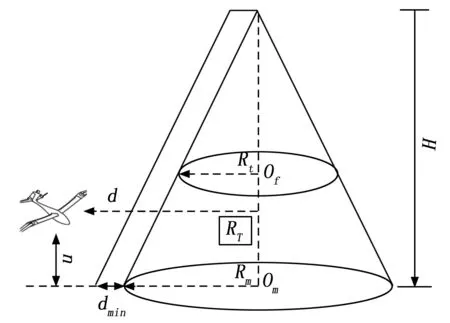
图1 地形威胁示意图

1.1.2 雷达威胁

雷达通过发射电磁波搜寻并分析空间内物体，获知物体的方向、高度和速度信息，进而达到侦查目的。雷达的威胁程度与其信号强度成正比，后者满足信噪比公式：

(4)

S/N表示雷达接收器的信噪比，Pt为雷达发射器功率，Gr为接收天线增益，Gt为发射天线增益，σ表示被探测目标的有效雷达散射面积。λ为工作波长，Ks表示波兹曼常数，Lm为损耗因子，Bn为滤波器带宽，Ts为工作时绝对温度，最后的dR表示无人机与雷达的距离，若仅考虑dR为变量，其余参数视为常数，则信噪比公式可简化为：

(5)

不难看出，雷达威胁关于距离的四次方成反比。

1.2 基本鲸鱼优化算法

WOA算法将种群个体的位置信息作为特征信息进行交互。澳大利亚研究学者Seyedali Mirjalili将座头鲸群捕食过程划分为3个阶段：包围猎物阶段、气泡网攻击阶段、以及搜寻猎物阶段。并提出三类更新机制：收缩环绕包围机制、螺旋更新机制、以及随机游走机制。采用何种机制由系数a及对应的|A|控制。系数生成方式为：

A=2·a·r-a

C=2·r

a=2(1-t/Max_iter)

(6)

(7)

螺旋式更新机制数学模型表示为：

(8)

式中，d表示当前鲸鱼与猎物—最优解之间的距离。b为对数螺旋的形状参数，一般设置为1，l为[-1，1]内的随机系数。

WOA算法采用随机游走机制模拟鲸鱼群的搜索猎物阶段。此阶段鲸鱼相互选择进行位置的随机更新。更新法则为：

(9)

三类更新机制关于系数|A|与随机概率p的关系可归纳为：

(10)

WOA依靠随机游走机制进行全局搜索，依靠收缩包围机制与螺旋式更新机制进行局部开发。

2 基于预警机制鲸鱼优化算法的无人机航迹规划

2.1 改进算法设计

2.1.1 混沌理论的初始化

目前几乎所有的群智能优化算法都属于随机性质的优化算法。鲸鱼群的初始化方式对算法的后续走向有着重要影响。使用传统的随机函数容易引入计算机的伪随机性。混沌映射可以用于替代伪随机数生成器，其生成的序列在解空间内分布较为均匀，因此能提高初始种群的遍历性。采用混论理论中的Logistic映射完成对算法随机初始化的改进，计算式表示为：

x(n+1)=μx(n)(1-x(n))

(11)

μ为可调参数，且μ∈[0，4]。除去Logistic映射，Tent映射也被广泛使用。式(9)定义的游走机制通过随机选取种群个体进行更新的方式，扩大了算法的搜索范围，一定程度提供了算法跳出局部最优的能力，但较优个体不可避免地会出现跟随较差个体随机游走地状况，出现个体搜索倒退、收敛缓慢的情况。为避免过度盲目性，以最优位置为导向，添加莱维飞行扰动保证一定程度的随机性。计算方法表示为：

(12)

式中，α⊕Levi(β)为莱维飞行添加项。其中⊕表示元素相乘，α为比例系数，β为参数，通常取1.5，μ与ν均为服从标准正态分布的随机参数。

2.1.2 预警机制的自适应概率选取

式(10)表明WOA执行螺旋式更新或其他两种机制取决于p，各自发生率为50%。概率p实质控制种群处于局部开发与全局搜索的何种阶段。本文依据个体适应度对种群个体的p数值进行自适应选取。对排名靠后的个体发出预警，适应度越差，在|A|>1时，其游走机率越大。在保持个体差异化的同时，优化收敛能力。个体概率pi表示为：

(13)

第i个体游走的概率与自身适应度排名有关，N为个体总数，rank(fitnessi)为个体适应度排名。游走概率pi限定在范围rank(fitnessi)。

2.1.3 自适应权重系数

收缩包围与游走机制处于|A|>1范围内，|A|<1范围内仍需进行探索能力与开发能力的平衡。在|A|<1内的螺旋更新机制内，添加权重因子w控制螺旋更新的范围，更新机制表示为：

(14)

其中：w参数的大小依据式(13)预警机制的概率pi决定，表达式为：

wi=0.75+pi

(15)

式(15)表明个体i的权重因子wi限定范围[0.75，1.25]。当wi<1时，收紧位置更新，当wi>1时，放宽位置更新，扩大更新范围。由wi所处范围不难看出收紧与放宽概率各占50%。

综上，APWOA算法的基本步骤如下：

APWOA的Python伪代码

Setting: lb, ub, N, D, ObjFun, and T

Logistic映射随机初始化种群位置;初始化种群最优解,式(11);

while (t<=T):

边界检测与处理;

根据航机代价定义公式计算种群个体适应度;

更新最优解best_fitness,best_position

for i inrange(1, N) do

根据适应度的排序计算各个体的预警概率p,式(13);

根据预警概率p计算出自适应权重w,

式(15);

Ifp< 0.5:

If |A|<1:

依据添加莱维飞行的游走机制更新位置信息,式(12);

else:

包围猎物,依据收缩包围机制更新位置信息,式(7);

else:

依据自适应权重的螺旋机制进行位置更新,式(14);

更新最优解best_fitness,best_position

t=t+1

end while

returnbest_fitness,best_position

2.2 考虑算法时间的航迹代价

常规航迹规划指标考虑无人机自身性能约束条件、以及地形威胁、雷达威胁等威胁条件。自身性能约束可分为角度代价、航程代价、高度代价。

航程代价指标是航迹代价函数的重要组成部分，航迹规划在多数情况下以寻求最短的安全可飞行航程为主要目标。算法规划得出的节点序列，将航路划分为对应的航迹分段，则总航程代价为各分段之和，表示为：

(16)

i为当前航迹节点，path为第(i，i+1)段航程，通过计算节点之间距离获得。

考虑爬升角/下滑角为主要角度代价指标。航迹序列中的每一个航迹段均需满足爬升角度与下滑角度的约束条件。超出最大角度约束则认为该航迹不可飞行，优化失败。

角度代价指标Jangle表示为：

(17)

若存在任意航迹段的爬升角/下滑角θi大于最大角度，则给予较大的惩罚值Ca，约束条件内，总的角度代价Jθ为各代价指标总和。Jθ越小，表明角度变化越小，则规划出的轨迹越平滑，这是角度纳入航迹代价的重要原因之一。

战场存在雷达威胁的条件下，还应考虑飞行高度代价指标。较高的飞行高度会加大被雷达发现的概率，而过低的飞行高度则难以应对起伏的地形。定义安全高度Hsafe为当前飞行高度与地面的最小安全距离。高度代价指标Jheight表示为：

(18)

威胁Jthreat主要考虑地形威胁与雷达威胁两种。式(2)为山峰地形威胁的计算方式。为保证存在雷达威胁情况下的无人机安全性，定义雷达绝对威胁领域，该领域内无人机毁伤概率为100%，则雷达威胁指标表示为：

(19)

dr为无人机与雷达j之间的距离，Rj为雷达j的领域半径，Cr为无人机落在领域内的惩罚值。由此可得总威胁代价Jthreat为：

Jthreat=Tterrain+Jradar

(20)

综上所述，本文定义常规航迹代价Jcost为：

Jcost=w1Jpath+w2Jangle+

w3Jheight+w4Jthreat

(21)

式中，Jpath为航程代价，Jangle为爬升角代价，Jheight为高度代价，存在雷达威胁的战场环境下，应控制无人机的飞行高度，Jthreat为威胁代价，包括第二章节提及的地形山峰威胁以及雷达威胁。w1，w2，w3，w4为各航迹代价的权重系数。

为完成实时航迹规划的实时性要求，本文将优化算法的求解时间内引入航迹代价函数。时间代价Jtime与航程代价Jpath具有相同的表达式，即为：

(22)

time为算法的实际运行时间，Tmax为预定的规划时间上限，应与威胁数量、规划距离成正相关。C为施加的惩罚值，惩罚值数值根据实际情况自定义选取，实时性要求极高的环境下，C可设置为无穷大，保证实时性的最高优先级。

综合常规航迹代价以及时间代价，总航迹代价Jtotal表示为：

Jtotal=α1Jcost+β1Jtime

(23)

α1与β1为常规航迹代价Jcost、运行时间代价Jtime相对应的权重系数。在实际使用时依据需求自适应选取，面临威胁环境复杂、远距离航迹情况，优先保证无人机安全抵达，应着重考量威胁代价以及航迹代价，可适当提高α1权重。反之，短距离、实时性要求高的情况，提高β1权重以增加机动性。

2.3 可变维度的航迹节点序列

WOA算法中，每个个体对应一条候选航迹规划，航迹的生成方法定义个体信息的表达方式。节点数量决定算法优化问题的维度。针对三维航迹规划，本文采用坐标等分法将其简化为二维航迹规划，以此，算法的优化维度简化为水平面内的(x，y)两个维度。x轴坐标等分法示意图如图2所示，仅为作图方便，山峰威胁与雷达威胁投影视为圆形。

图2 x轴坐标等分法示意图

单独使用x坐标等分法或y坐标等分法会造成算法模型失效的风险。如只采用x坐标等分法，模型会在无人机起始点与目标点x轴坐标相等情况时失效，且当x坐标变化远小于y坐标变化时，计算的规划航迹点过少，导致航迹不具有飞行价值。为防止上述问题，本文采用联合坐标等分法。选取x坐标等分法与y轴坐标等分法的结果最大值确定航迹待规划节点数量。避免单一坐标等分法失效的同时，规划较多数量的节点保证航迹的可行性。节点数量pointn表示为：

(24)

step为规划步长，固定起始点与目标点情况下控制节点数量，改变step即实现航迹规划问题的维度。航迹规划节点之间，常使用采样的方法进行碰撞点检测，起到降低规划维度的同时还可以对轨迹完成优化。虽然改变起始点与坐标点的方法可以实现对不同维度的算法仿真，但会引入不同雷达威胁与山峰威胁，变量过多导致对比困难。本节设计步长step控制的可变维度航迹生成方法则更方便仿真数据对比。

3 仿真实验与分析

3.1 基准函数测试与分析

基准测试函数是进行算法性能测试的基本工具，为分析本文改进WOA算法的优化性能，采用文献提及的18个广泛使用的基准测试函数进行性能测试。选取群智能优化算法中典型的PSO算法、原WOA算法[11]、使用莱维飞行该进的灰狼算法LGWO[20]，以及文献最新改进的基于莱维飞行的WOA算法LWOA[21]进行测试比较。测试函数的基本信息参考文献[22]。仿真实验的硬件平台为联想笔记本AIR14计算机，运行内存为16 g，CPU为AMD Ryzen 4800U，集成显卡为AMD 512mb。软件平台为：MATLAB R2016b，以及Pycharm 2021。

设置种群数目为30，迭代次数500次。除此之外，上文提及的对比算法的必要参数设置如表1。关于基准测试函数，f1～f5为高维基准函数，选定维度为30。f14～f18为多峰值基准函数，维度以及搜索范围遵循自定义。为降低实验偶然性，每类算法独立运行30次取平均值。测试结果(最小值、平均值、方差)汇总至表2。

表1 各算法参数设置

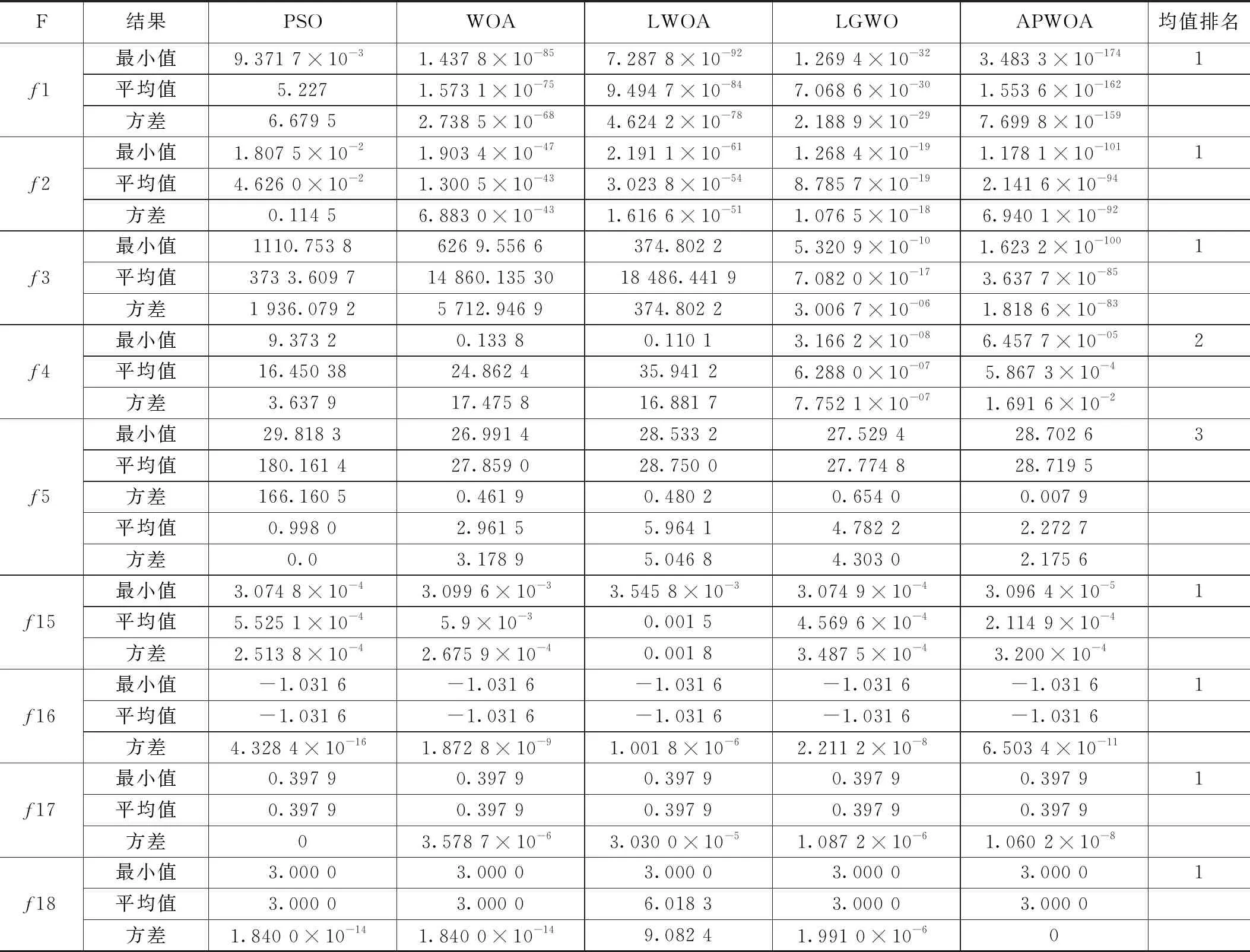
表2 基准函数测试结果

f1～f5的高维函数测试中，WOA算法相比PSO算法，本身就具有较高的收敛能力。但本文改进的APWOA算法比只添加莱维飞行扰动的LWOA算法具备更高的收敛精度与收敛稳定性。APWOA在f1～f3的测试中表现出优异特性，但APWOA与LWOA算法在f4～f5表现落后于LGWO算法。关于多峰函数f15～f18测试，APWOA能够搜索出f16～f18的理论最优解，并在f15上搜索出相比于其他算法的较小值。综合而言，基准函数的测试仿真表明，在保证低维函数的局部寻优能力的同时，APWOA在高维函数的收敛速度与精度得到明显改善。

3.2 三维航迹规划测试

为验证改进的APWOA算法对于时间约束的航迹规划的有效性，基于Pycharm开发平台和python开发语言进行仿真验证，并使用Matlab2016b进行数据处理与图像绘制。

3.2.1 变维度的航迹求解精度测试

仿真场景数据由式(1)计算得出，DEM的范围为100 km×100 km×500 m。式(1)地形函数设置为a=0.1、b=0.01、c=1、d=0.1、e=0.2、f=0.4、g=0.02。除去基础地形外，添加雷达作为战场威胁的代表。初始两个雷达的水平面坐标为(65，10)、(12，85)。雷达不可飞行的区域半径为10 km，设定该领域内无人机毁伤概率为100%，领域外雷达威胁遵从式(5)计算。航迹代价求解的维度为待规划的节点数目，本文使用改变步长的方法实现节点数目、以及维度的变化。航迹步长分别选取8 km、5 km以及3 km。为进行维度变化的测试，选定起始点为(3，3，60)，目标点为(92，58，60)，并固定每个航迹分段的碰撞点检测数目，以控制计算量的数据误差。比较上文基准函数对比试验参与的PSO算法、WOA算法与本文的APWOA算法的航迹解。为同时获取算法收敛精度与收敛速度信息，迭代次数选取200次。每类算法的每个步长维度运行10次取平均值，汇总结果(平均航迹代价、单次迭代运行时间、运行方差)至表3。

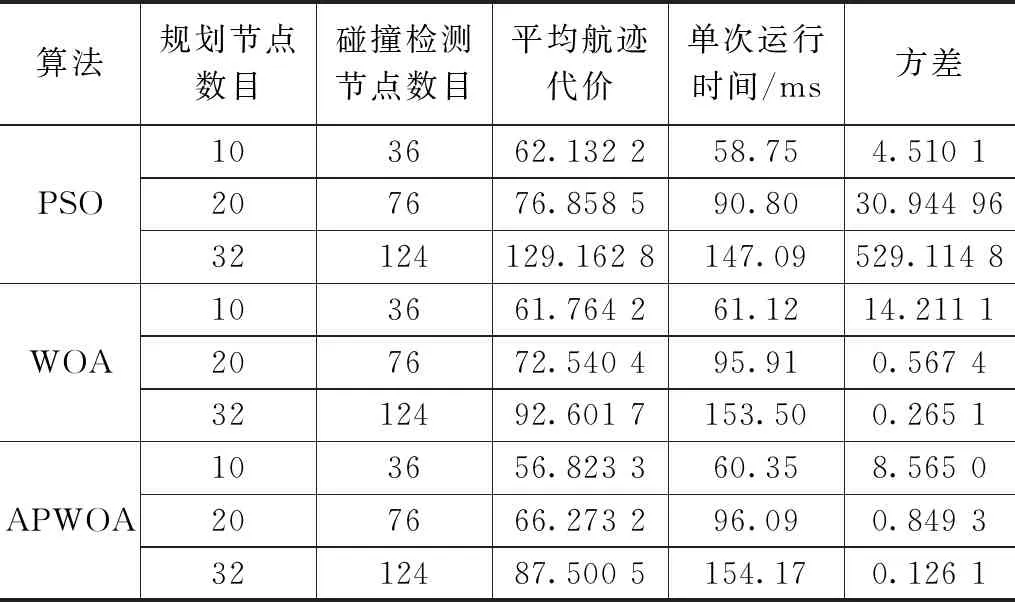
表3 不同维度的航迹规划测试结果

从表3看出，APWOA算法以及WOA算法相较于PSO算法，面对高维航迹规划仍然可以得出较优解，且规划解优势明显。而相较于WOA算法，APWOA算法在运行时间基本持平的情况下，可获得代价更小的规划解。10维度规划中相较WOA算法提升8.0%，32维度规划中相较WOA算法提升5.5%。这表明APWOA算法具备更高的收敛精度。实际航迹规划采用的步长应根据目标点起始点距离、地形复杂度、威胁数目综合考量，部分文献甚至设有最小规划步长。表中选取20，30高维度情况多作为极限测试以及数据分析使用。根据表3，实验选取3种算法的航迹均值作为典型代表，关于8 km步长10维度的航迹规划路线如图3所示。关于3 km步长32维度的航迹规划路线如图4所示。

图3 8 km步长的航迹规划结果对比

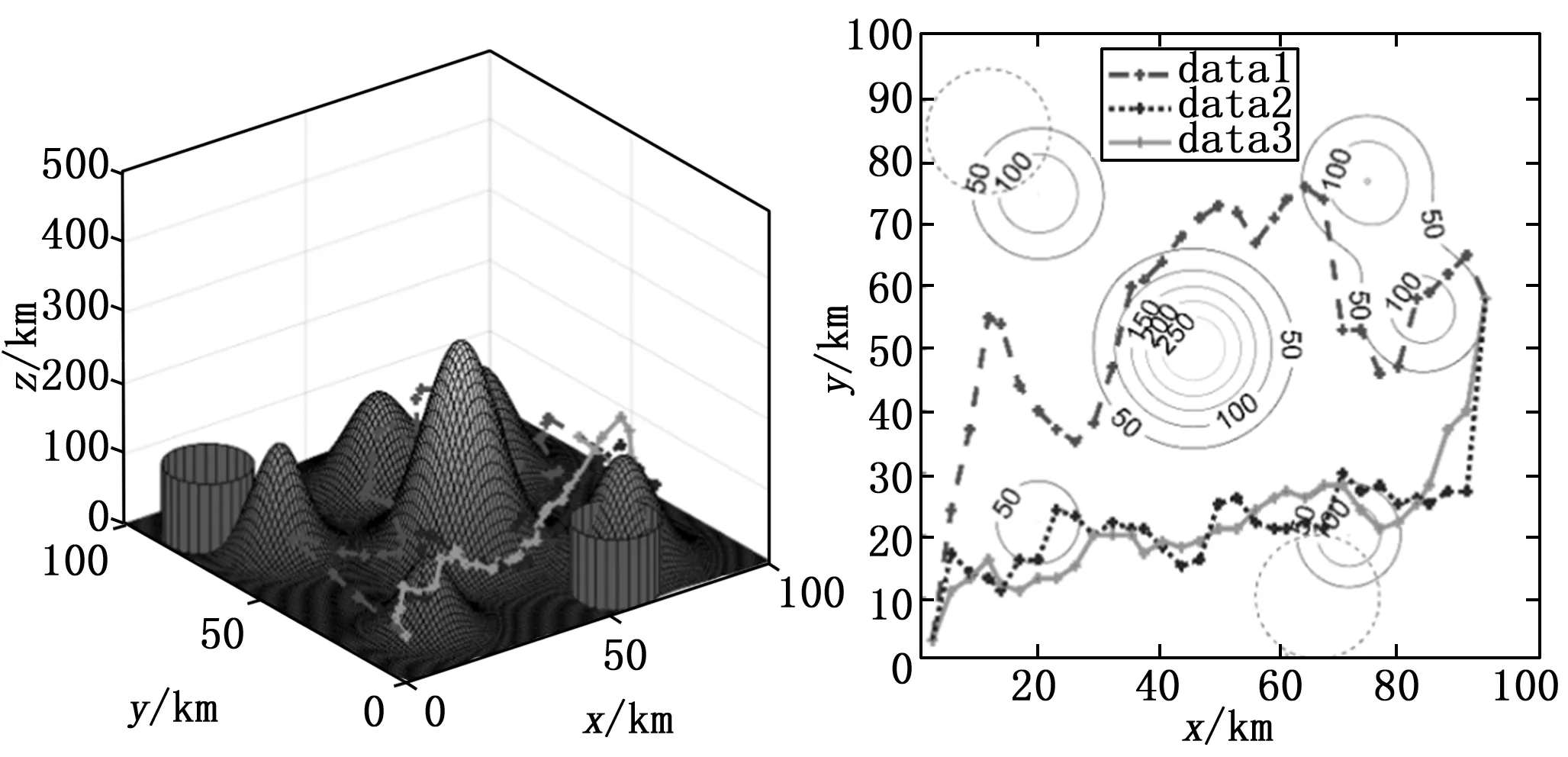
图4 3 km步长的航迹规划结果对比

图3中，在8 km步长，维度较低的测试中，3种算法均可以搜索到可飞行的航迹路线。其中APWOA算法规划出的路线最短，表明其优化能力相对较强，PSO算法相对于其他算法，相同迭代次数花费较少的运行时间，所以3种算法求解出的时间约束的航迹代价差距较小。在图4的3 km步长的高维度测试下，APWOA算法解算出的航迹代价则远优于PSO算法，相较于原WOA算法也具有明显提升。

3.2.2 航迹求解实时性测试

使用上节的测试数据，取3 km步长与8 km步长规划中接近航迹代价平均值的测试路线，绘制3种算法关于迭代次数的收敛曲线，如图5所示。

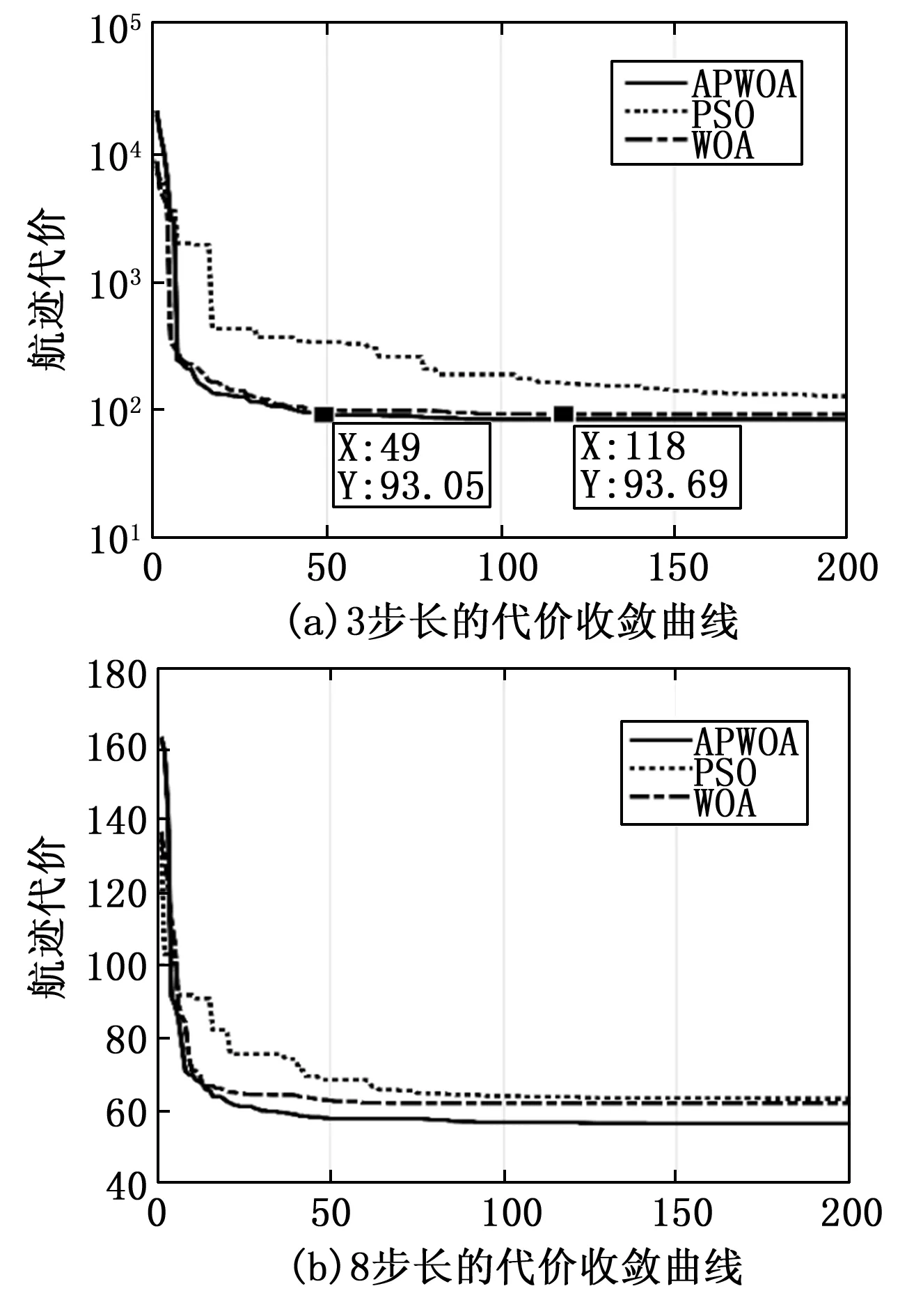
图5 不同步长各算法的收敛曲线

图5(a)中，APWOA早69次迭代获得WOA算法可获得的最优解，依据表3中WOA的单次迭代运行时间，则APWOA算法在3 km步长32维度的极限测试下可节省时间成本6.7 s左右，占WOA算法总用时的58.5%。在正常维度的(b)图中，基于APWOA算法的航迹规划实时性依旧具有不俗提升，APWOA算法20次迭代内即可获取优于WOA算法的航迹代价，总耗时1.2 s。

4 结束语

本文针对无人机三维航迹规划问题，主要进行两方面的改进研究。针对航迹优化模型，将算法运行时间计入航迹代价，建立起规划航迹与运行时间的互反馈通道。针对优化求解算法，本文提出基于预警机制的鲸鱼优化算法。对3种机制的选取概率实现自适应，并依次概率实现对螺旋更新机制的收缩控制，实现全局探索与局部优化的平衡。关于算法验证，使用可变维度的航迹生成方法，验证了算法的有效性与优越性。