基于遗传算法优化粒子群算法的支斗两级渠系优化配水研究

高 建，张运鑫，2

（1.河北工程大学水利水电学院，河北 邯郸 056038；2.河北省水资源高效利用工程技术研究中心，河北 邯郸 056038）

0 引 言

中国是世界上13 个贫水国家之一。2021 年我国用水总量为5 920.2 亿m³，其中农业用水量3 644.3 亿m³，占总用水量的61.5%[1]。水资源短缺问题日益成为制约我国农业和经济社会发展的重要因素。因此，优化灌区输配水渠系运行管理对提升灌区渠道输配水效率，改善灌区灌溉供用水状况具有重要意义。

明渠是被广泛应用于灌区的输配水方式[2]。灌区输配水渠系一般由干、支、斗、农、毛五级渠道构成，其中支、斗两级渠道是灌区渠系配水由续灌转变为轮灌的关键衔接部分，对实现灌区渠系优化配水和提高渠系水利用系数方面具有重要作用。

有学者对支、斗渠合理配水调度进行了研究，Suryavanshi和Reddy提出将轮灌分组问题转化为数学问题，引入了流管概念，将0-1规划模型中的二元决策变量Xij看作第i个流管的第j个分水口，它的值为0或1，0表示该分水口关闭，1表示该分水口打开[3]，通过这种数学规划的方式获得最优配水调度方案。吕宏兴等改进了Suryavanshi 的模型，通过进行引水时间的均一化处理，解决了渠道配水时需要多次调节进水闸的问题[4]。

目前，大多数灌区仍凭借以往管理经验来确定灌溉渠系的水量和流量分配，即采用经验配水法。尽管采用经验配水方法可以进行灌区配水，但经常出现渠系输配水时间长、小流量配水以及水资源浪费等问题。经验配水方法无法实现精准配水，也难以对供需变化做出及时响应[5]。随着水资源供需矛盾日益加剧，对提升灌区供需水管理水平的要求也越来越高[6]。为了实现渠系的高效优化配水，学者们开始研究将智能优化算法引入到渠系配水中，如遗传算法[6-12]、粒子群算法[12-15]、模拟退火算法[16]、灰狼优化算法[17]等，通过对这些算法应用获得渠系最优调度方案。马孝义等建立了下级渠道引水流量不相等情况下的渠道优化配水模型，通过遗传算法获得优化配水方案，输水损失更低[9]；刘照等以渠道输水损失最小与轮灌组间引水持续时间差异值最小为目标建立多目标优化配水模型，通过双层粒子群算法求解优化方案，不但可减少渠道弃水量，同时统一了轮灌组闸门关闭时间，减少了闸门启闭次数[13]；刘叶等以渠系输水损失最小为目标构建两级灌溉渠系优化配水模型，通过遗传算法确定的方案，不但能满足灌溉要求，同时减少渠系配水时间以及闸门启闭次数[10]；徐淑琴等以灌区渠道输水损失最小及干渠水位变化均匀为优化目标，运用带精英策略非支配排序遗传算法确定运行方案，在满足优化目标的前提下，可以缩短各生育期的配水时间，且流量变化幅度较小[11]。

针对优化离散空间约束问题，Kennedy 和Eberhart 在传统粒子群算法(PSO)基础上改进并提出离散二进制粒子群算法(BPSO)[18,19]。本文在已有研究基础上，综合考虑离散二进制粒子群算法(BPSO)和遗传算法(GA)的优缺点[20]，研究提出了混合二进制粒子群算法（GA-BPSO），用于灌区支、斗两级渠系优化配水研究。用二元决策变量Xij描述每一个支渠向斗渠配水的分水口配水运行状态，其中赋值0表示该分水口关闭；赋值为1 则表示该分水口开启。应用MATLAB 对BPSO 算法和GABPSO算法进行模拟计算，并通过应用案例进行检验分析。

1 支斗渠系优化配水模型

当支渠向斗渠配水时，往往将斗渠分为几个组，按照“组间续灌，组内轮灌”的模式运行，支渠向斗渠配水灌溉如图1所示。

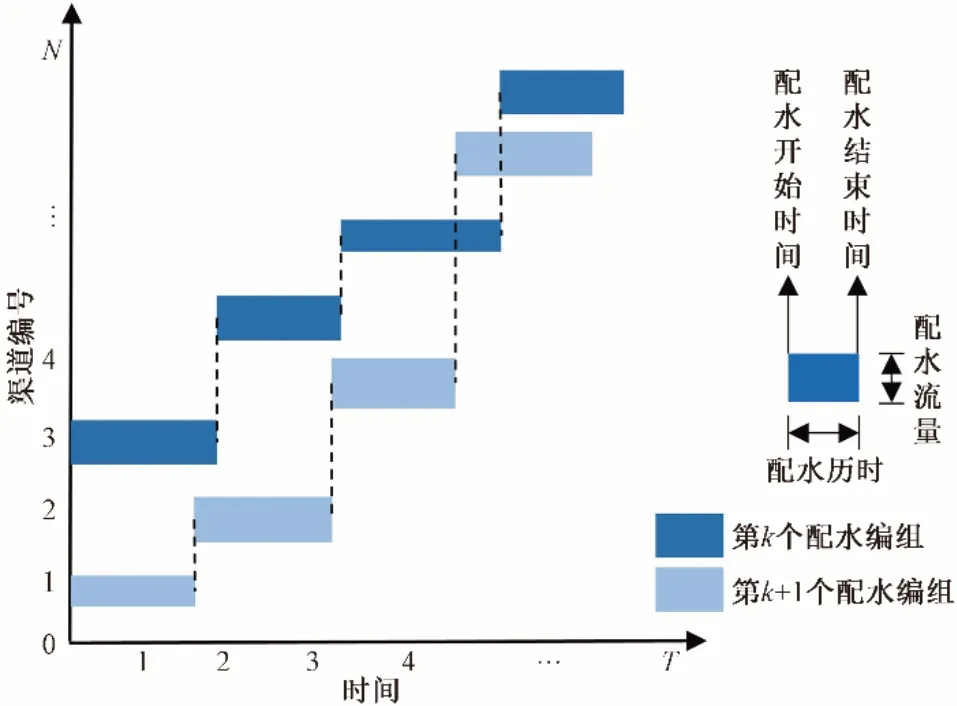
图1 支渠向斗渠配水示意图Fig.1 Irrigation schematic from branch canal to lateral canal

设支渠的净流量为Q净，各斗渠的流量为q，斗渠渠道水利用系数为η，并用向上取整公式ceil 和向下取整公式floor 进行取整，灌溉编组数M计算公式如下：

本研究提出的模型以支渠向斗渠输配水运行时间最短作为目标，模型的决策变量主要包括灌溉组数、分水口数和每个分水口的连续引水时间。约束条件包括引水流量和任意分水口开启次数等，优化模型如下：

式中：Tb表示支渠运行时间，s；Tl表示M 个灌溉斗渠编组中运行时间最长的灌溉斗渠编组运行时间，s；M 为灌溉编组个数；N 为被配水斗渠条数；ti为第i 组灌溉斗渠编组运行时间，s，其中i=1,2,…,M；tj表示第j条斗渠配水运行时间，s，其中j=1,2,…,N；Sj表示第j 条斗渠所需的灌水量，m³；qj表示第j 条斗渠配水流量，m³/s；ηj表示第j条斗渠渠道水利效率；Xij表示第i个灌溉编组中第j个分水口的状态，Xij=0 为i个灌溉编组中第j个分水口是关闭状态，即第i个灌溉编组内的第j个分水口没有配水计划；Xij=1 为i 个灌溉编组中第j 个分水口是打开状态，即第i个灌溉编组内的第j个分水口有配水计划。

约束条件如下：

设第i 灌溉编组供水时间为ti，则其总供水时间不应大于灌溉周期T，即：

任意分水口在灌溉周期T内只能开启一次，即：

决策变量取值约束：

各灌溉斗渠编组净流量之和不大于对应支渠来水净流量，即：

式中：Qi表示第i个灌溉斗渠编组的净流量，m³/s。

2 混合二进制粒子群算法

2.1 粒子群算法原理（PSO）

传统粒子群算法（Particle Swarm Optimization，PSO）[18]是在连续区域内对所求问题进行优化求解的一种算法，粒子群中的每一个粒子个体均表示一种可行的解决方案，其算法原理是通过粒子之间的简单行为，经过交互得出最优解，具有较快的收敛效率和局部搜索能力但容易陷入局部最优解的特点。

粒子群算法的基本求解计算表达式如下：

式中：v(i)(t)表示第i 个粒子在第t 次的移动速度；x(i)(t)表示第i个粒子在第t次粒子所在的位置；x(i)(t+1)表示第i个粒子在第t+1次所在的位置；c1、c2为粒子的学习因子；rand1、rand2为分布在[0,1]的随机数；p(i)best为第i个粒子历史最优解；gbest为当前历史最优解。

进一步分析可将式(10)中第i个粒子在第t+1次的移动的速度可分解为三部分：w v(i)(t)为第一部分，称为“惯性”部分，这一部分反映了粒子原有的运动趋势；c1rand1[p(i)best-x(i)(t)]为第二部分，称为“个人认知”部分，这一部分就反映了粒子向自身粒子最优解移动的趋势；c2rand2[gbest- x(i)(t)]为第三部分，称为“社会认知”部分，这一部分反映了粒子向全部粒子中的最优解移动的趋势。粒子移动过程图和粒子群算法基本流程图分别如图2和图3所示。

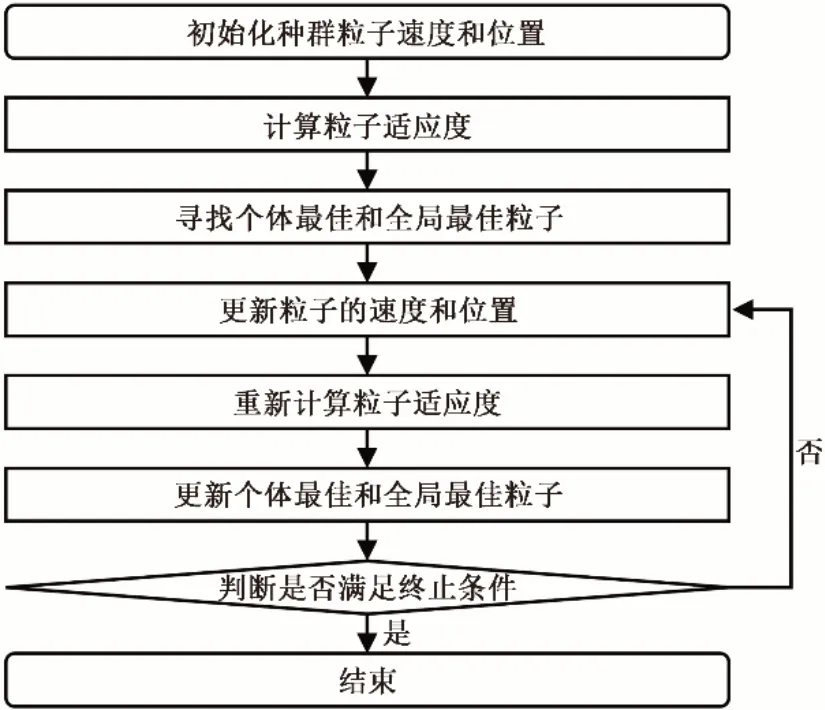
图2 PSO流程图Fig.2 Flow chart of PSO

图3 PSO粒子移动过程图Fig.3 PSO particle movement process diagram

典型粒子群算法步骤如下：

（1）按照需求对粒子进行初始化，包括粒子速度和粒子位置；

（2）构建适应度函数，对每个已经生成的粒子按照适应度函数计算相应的适应度；

（3）根据已经计算出的适应度评价出个体最佳粒子以及全局最佳粒子；

（4）根据公式（10）和公式（11）更新每个粒子的速度和位置；

（5）重新计算更新过后的每个粒子的适应度；

（6）重新计算过后的适应度与个体最佳粒子和全局最佳粒子进行比较，重新选出个体最佳粒子和全局最佳粒子；

（7）依照结束条件进行判断，满足结束条件结束算法；若不满足则重复执行上述步骤4）、5）、6）直到满足条件。

2.2 离散二进制粒子群算法原理（BPSO）

Kennedy 和Eberhart 为解决离散型或二进制类型的问题从而改进了常规的粒子群算法，提出了离散二进制粒子群算法（Discrete Binary Particle Swarm Optimization Algorithm，BPSO）[19]。该算法是采用二进制编码0或1对粒子中某一维度的状态进行表示，速度更新公式同基本粒子群算法的速度更新公式相同，但没有使用粒子群算法位置更新公式，取而代之使用sigmoid函数将速度值映射到[0,1]区间，以此表示取0或1 的概率。通过rand 随机数与sigmoid 函数映射之后的值进行比较，得到位置的具体值[21]。

下式分别为sigmoid函数以及位置更新公式：

2.3 遗传算法（GA）

遗传算法（Genetic Algorithm，GA）借鉴了达尔文的进化论和孟德尔的遗传学说，是通过模拟生物在自然环境中的遗传和进化的过程而形成的一种自适应全局优化搜索算法，具有全局搜索能力强，局部搜索能力较弱的特点[20]。图4 为遗传算法流程图。

图4 GA流程图Fig.4 Flow chart of GA

其算法流程大致如下：

（1）按照编码需求（二进制编码，实数编码等）对种群进行初始化；

（2）构建适应度函数，对每个已经生成的个体按照适应度函数计算相应的适应度；

（3）根据需求对已经生成的个体进行选择，一般选择适应度较高的个体为父代；

（4）按照设定好的交叉概率及交叉规则，将选择出来的父代进行随机配对，进行交叉运算，生成新的个体；

（5）按照设定好的变异概率及变异规则，将选择出来的父代进行变异操作，生成新的个体；

（6）重新计算适应度并更新种群；

（7）依照结束条件进行判断，满足结束条件结束算法；若不满足重复执行上述步骤（3）、（4）、（5）、（6）直到满足条件。

2.4 混合二进制粒子群算法（GA-BPSO）

根据GA 和BPSO 的特点，在BPSO 的基础上融入GA 的方法，融合两种算法的优点并弥补相应不足，得到一种整体性能更优的混合二进制粒子群算法(GA-BPSO)。图5为GA-BPSO基本流程图。

图5 GA-BPSO流程图Fig.5 Flow chart of GA-BPSO

其算法流程大致如下：

（1）按照需求对粒子进行初始化，包括粒子速度和粒子位置；

（2）对每个已经生成的粒子按照适应度函数计算相应的适应度；

（3）根据已经计算出的适应度评价出个体最佳粒子以及全局最佳粒子；

（4）根据公式（10）更粒子新速度，根据公式（12）、（13）更新粒子的位置；

（5）计算更新后的粒子适应度；

（6）重新选出个体最佳粒子和全局最佳粒子；

（7）按照需求选择出一定数量的个体作为父代，并进行交叉的相关操作；

（8）按照需求选择出一定数量的个体作为父代，并进行变异的相关操作；

（9）对新生成粒子进行适应度计算，根据结果更新粒子并重新选出个体最佳粒子和全局最佳粒子；

（10）依照结束条件进行判断，满足结束条件结束算法；若不满不足重复执行步骤（4）、（5）、（6）、（7）、（8）、（9）直到满足条件。

3 实例应用

某灌区一条支渠下有7 条斗渠，支渠设计流量2.5 m3/s，渠道水利用系数为0.92，各斗渠设计流量、控制面积以及渠道水利用系数如表1 所示。支渠灌溉周期为7 d，本次灌水定额确定为900 m3/hm2，优化配水目标为渠系输配水时间最短。

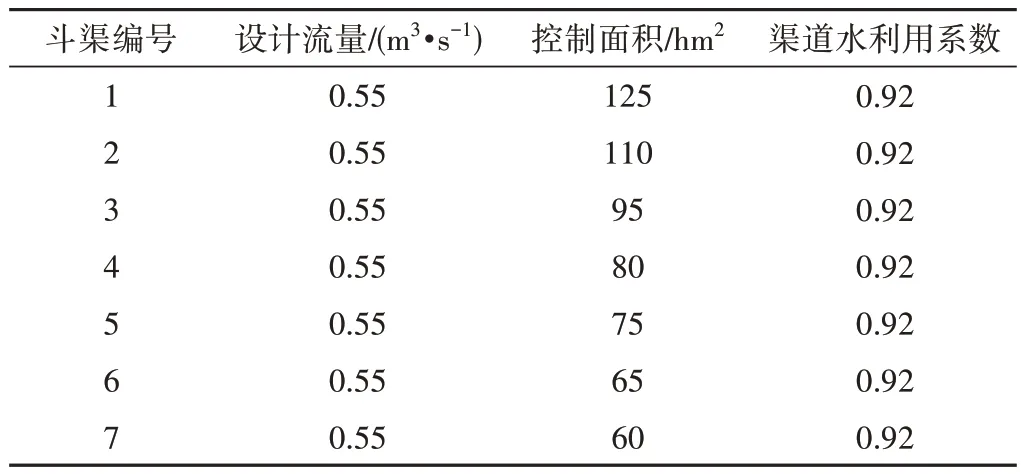
表1 各斗渠参数Tab.1 Parameters of each lateral canal

3.1 案例分析

根据该灌区支渠、斗渠相关信息以及公式(1)确定灌溉编组数M=4 最佳。根据相关约束可知每条斗渠只能在一个灌溉编组中运行，结合算法可将每一条斗渠看作一个1×4 的列向量，均由0 或1 组成。其中0 代表该斗渠在某灌溉编组内的配水口为关闭状态，即该灌溉编组内该支渠没有配水计划；1代表该斗渠在某灌溉编组内的配水口为打开状态，即该灌溉编组内该斗渠有配水计划。如[1,0,0,0]T表示该斗渠在第一个灌溉组中运行，而不在其余灌溉组中运行，示意如图6(a)所示。

图6 算法分析图Fig.6 Algorithm analysis graph

按照上述设想，如果将灌溉编组和渠道成生一个只包含0或1 的二维数组，初始化各灌溉斗渠编组分水口状态如表2 所示，则当前配水状态为7条斗渠均在第一个灌溉编组中，其余灌溉编组无斗渠配水计划，按此设定方式会降低算法的运行效率。所以对BPSO 的粒子初始化做出改变，在生成粒子时，生成一个7 维的向量，每一个维度可看成每一条斗渠变化状态，其中：假设这个粒子初始化时为[0,0,0,0,0,0,0]，当粒子某一维度发生变化时则对应斗渠分水口在灌溉编组中工作状态就会发生变，从第i个灌溉编组变换到第i+1个，具体如图6(b)所示。当粒子由[0,0,1,0,0,0,0]变为[0,0,0,0,0,0,0]则第三条斗渠会从第三个灌溉编中有配水计划变为在第四个灌溉编组中有配水计划。当某斗渠在最后一个灌溉编组中有配水计划时下一次变换就会变换到在第一个灌溉编组中有配水计划；如果粒子某一维度未发生改变则对应的斗渠分水口在灌溉编组中的状态就保持不变。

表2 初始化各灌溉斗渠编组分水口状态Tab.2 Initialize the status of each irrigation lateral grouping manifold

3.2 算法应用

本文在PC 端使用MATLAB 软件求解算法。将渠系配水时间作为适应度函数值，最佳配水方案将具有最小的适应度函数值。算法参数确定：种群Z=20，迭代次数N=100，惯性权重W=0.9，个体学习因子C1=2，社会学习因子C2=2，交叉概率Pc=0.7，变异概率Pm=0.05。按照公式（1）确定灌溉斗渠分组数M=4，根据各灌溉斗渠编组分水口状态，按照公式（4）计算出每个灌溉斗渠分组运行的时间ti，再根据公式（3）得出所有ti运行时间最长的灌溉斗渠分组运行的时间Tl，将Tl作为算法的适应度函数值，使其尽可能小以达到算法求解要求。

3.3 结果分析

针对上述两级渠系输配水问题案例，可得到如下分析：

（1）两种算法得到的配水编组的方式都可以将渠系配水时间降到最低，具体方案如表3和表4所示。

表3 BPSO和GA-BPSO计算最优配水方案结果（1）Tab.3 Results of BPSO and GA-BPSO calculations of optimal water distribution schemes (1)

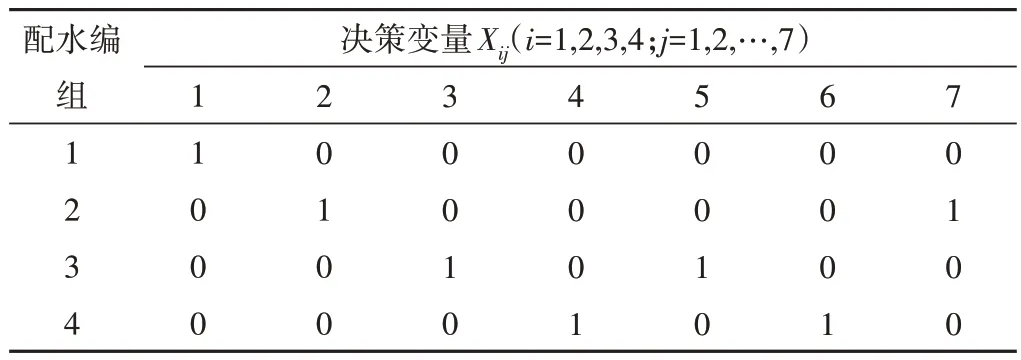
表4 BPSO和GA-BPSO计算最优配水方案结果（2）Tab.4 Results of BPSO and GA-BPSO calculations of optimal water distribution schemes (2)

（2）通过表5 以及图7 可知，在参数相同的情况下BPSO在大概21 代左右能得到最优解，而GA-BPSO 则在大概12 代左右得到最优解，且两者最优解相同。可见，针对BPSO 的不足之处结合GA 之后的新算法GA-BPSO 的整体性能优于BPSO。

表5 BPSO和GA-BPSO迭代终止时的性能对比Tab.5 Performance comparison between BPSO and GA-BPSO at iterative termination

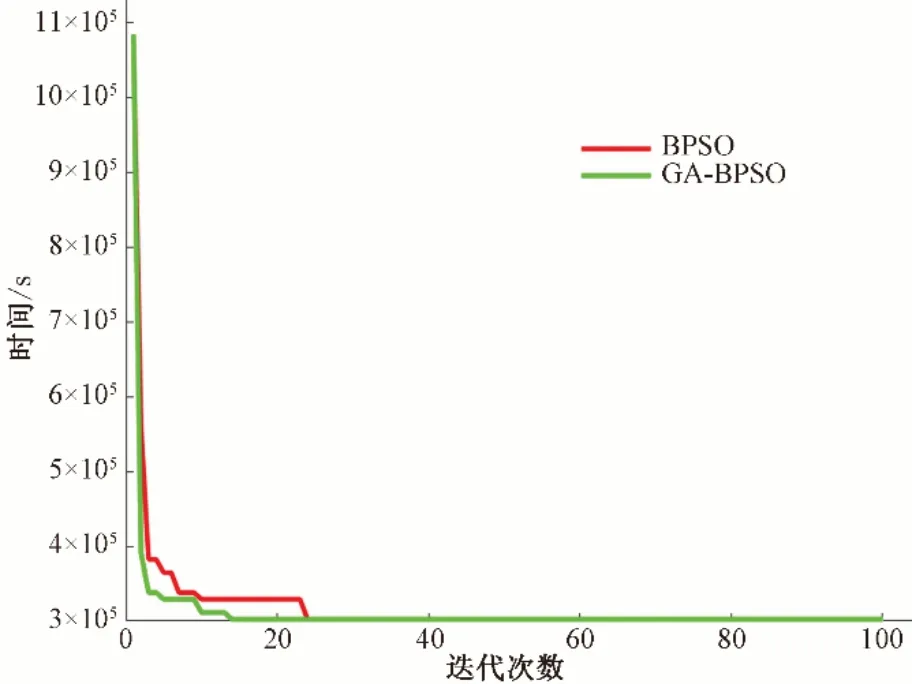
图7 算法结果对比Fig.7 Comparison of algorithm results

（3）由于在BPSO 中包含速度和位置两个变量，在与GA结合时交叉、变异操作会导致速度、位置均发生相应改变，而速度变化会影响下一次迭代时位置发生改变的概率，所以在模拟过程中会出现个别GA-BPSO效果不如BPSO的情况。

4 结 论

本文针对灌区支斗两级渠系输配水优化问题，根据BPSO和GA的优缺点，在BPSO基础上融合GA的思想，构建一种更为高效的GA-BPSO。通过GA-BPSO 对案例问题进行优化，模拟结果表明GA-BPSO 达到最优解的平均收敛代数要比BPSO达到最优解的平均收敛代数要低，说明结合后的GA-BPSO 的整体性能相比BPSO 要更好。证实了支斗两级渠系在“组间续灌，组内轮灌”的输配水模式下GA-BPSO 具有更好的可行性和高效性，可为灌区用水调度提供一种较优的解决方案。由于遗传操作对速度的改变可能会对下一次迭代时位置的改变产生影响，在未来算法优化的方向上可以进一步研究GABPSO 运行过程中的速度更新方式及更高效的交叉、变异方式。