数线估计及其教学意蕴

徐玉嫚，陆世奇，徐文彬

数线估计及其教学意蕴

徐玉嫚，陆世奇，徐文彬

（南京师范大学 课程与教学研究所，江苏 南京 210097）

数线估计是衡量和预测儿童数学能力的一个重要工具．儿童在NLE上的表现体现了其对数字的理解，NLE的准确性越高，意味着儿童在数学方面有着更大的成就．已有研究表明：NLE分有界NLE和无界NLE两种；个体表征数字的模型包括线性模型、对数模型等；影响NLE表现的因素包括NLE的不同类型与数值范围和家庭经济状况与文化教育等外部因素，以及个体的数学认知能力和认知加工过程等内在因素．结合数线和NLE的特点，在教学中，教师可以将其作为辅助学生学习的工具，运用无界NLE丰富识数计数教学，发展学生的数感、运用有界NLE辅助比例知识教学，发展学生的推理和测量能力等，以促进学生数学认知及其它数学能力的发展．

数线；数线估计；数字心理表征；影响因素；教学意蕴

1 问题提出

“数”与“形”是贯穿数学教育的两条主线，“数”与“形”的相互转化、结合也是数学解题的重要方法[1]．数线（Number Line，NL）是数与形相结合的典型．首先，数线是一种“形”，它以线的形式呈现．其次，数线本身就是一种“数形结合体”，数线上，数字按照顺序排列，每个数字在线上都有自己的位置，“数”在“形”上得以体现并与之结合．最典型的就是数轴，它规定了原点、正方向和单位长度，由于它严格拥有三要素，一些研究者也将其称为结构化数线[2]．最后，数线也有其自身的“形”，且并不局限数轴，它可根据具体的情境和学习需要进行变换，在不同的表现形式中将“数”与“形”结合起来．例如，双数线能够帮助理解比例知识，直观展示两个量之间的共变关系[3]．空数线（没有任何端点和数字标记的一条线）则可用来让学生进行心理计算的时候记录和分享他们的思考策略，是增强学生心算能力的有力工具[4]．数线正是以这样的特性达到“以形助数”，启发学生触及问题的本质与核心，培养直观思维与抽象思维，发展学生的数学认知能力．

数线估计（Number Line Estimation，NLE）是依据数线特点所设计的一种数字估计任务．它以数线为载体，将“数”“形”“估计”相结合，是测量儿童数字估计能力的一项重要工具．数字估计对数的认知具有重要意义，数字估计能力也是儿童早期数学认知能力发展的关键，它可帮助儿童建立关于数字顺序、数量大小、数字之间相互关系以及数字空间表征的相关概念[5]．国内外对儿童数字估计的相关研究中，数线估计扮演了重要角色，常被用以展开对儿童数学学习与认知、能力发展或心理发展等的研究[6-7]，如追踪个体成长过程中不断增长的数字知识[8]、对数字量级理解的发展[9-10]等．

从操作的角度来看，数线估计属于一种空间—数字任务．诸多研究揭示，空间任务完成得好的人，其数学方面的表现也较为优异[11-12]，空间—数字任务的提升有助于提升儿童早期的数学能力[13]．通过对儿童进行数线估计任务训练，其数学成绩能够得到有效提高[14-16]．若能在教学过程中合理运用数线及数线估计，或许可以对学生的数学学习和能力发展产生一定的促进作用．但在已有研究中，数线估计更多地是被作为一种实验工具，较少有研究探讨其在教学情境中的运用、对于教学的意义．因此，将聚焦数线估计任务，从数线估计类型、数线估计的心理表征模型、数线估计表现的影响因素等方面来探讨数线估计所应有的教学意蕴．

2 数线估计

2.1 数线估计的内涵——估计与数量估计

数量估计是估计的主要类型之一，是指在不同数量表征之间转换的过程，这些数量表征可能是数字的也可能是非数字的，其中至少有一个数量表征是不精确的[6]，其本质是一种导致数字判断的数学解决问题的形式，它反映的是一种高水平的认知加工过程[17]．数线估计属于数量估计的一种，同时还体现了估计的核心——数值表示和空间表示之间的转换[18]，是一种跨模态匹配任务，因为它要求参与者将数字与相应的线的长度相匹配．数线估计分为两种情况：数字—位置（number-position，NP）任务，即个体对给定的某个数字（即目标数字）在数线上所对应的位置进行估计；以及位置—数字（position-number，PN）任务，即个体估计数线上某个点所对应的数字．目前已有的相关研究大多采用经典的NP任务，对PN任务的使用则相对较少[19]，因此，后续相关研究可以加强对同样经典的PN任务的使用，或许会有不一样的发现．

NLE的一个主要衡量指标是估计的准确性，即个体对数字的估计位置与其实际位置之间的符合程度．根据Siegler等的研究，数线估计的准确性是用绝对误差百分比（percent absolute error，PAE）来表示的，其计算公式为=（估计值—正确值）/被估计的数字范围|×100%[6]．也就是说，如果要求学生在一个0～100的数线上估计52的位置，而他将标记点放在了60的位置上，那么估计的准确度记为8%（=|(60-52)/100|×100%）．的值越高，数线估计的准确度就越低．但不管数线估计所涉及的过程如何，更高的准确性预示着在数学方面有更大的成就[9]．

2.2 数线估计的类型——有界数线估计和无界数线估计

传统意义上的数线估计任务是有界数线上的数字—位置任务，称为有界数线估计任务．有界NLE有特定的数字范围（如0到100，0为左侧端点，100为右侧端点），参与者被要求估计给定数字的位置，给定数字通常呈现在数线的正上方（如图1所示）．自Sigler等在其研究中推广使用有界数线估计之后，许多研究都是围绕其开展的，并把它作为测量和培养儿童数感的重要工具[20-22]．Siegler等人认为，儿童在有界NLE任务上的表现有效地表明了儿童潜在的数字心理表征，是儿童对数字理解的直观体现，因而数线估计所测量的核心能力就是个体的量级表示能力[6，18]．Opfer等指出，有界NLE为直接测量儿童潜在的数量表征提供了一个相对简便的理想模板[23]，原因在于“线本身的长度在心理上并不具有压缩性或延展性”，从而可以评估儿童如何在心理上压缩数字以把它们表征在数线上．

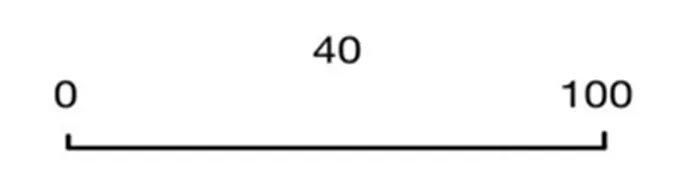
图1 在0～100范围的有界数线上估计40的位置

有部分研究者对有界数线估计能够直接推断数字量级的心理表征这种观点提出了质疑，他们认为有界数线任务存在自身的局限性：由于有界数线存在着规定的端点，会限制估计中可能出现的错误及程度，即左侧端点限制了个体低估小值的可能，右侧端点限制了个体高估大值的可能[24]．儿童之所以能成功进行有界NLE任务是因为使用了适当的策略，只有对这些策略进行研究才能够揭示出儿童潜在的数量表征．

这些研究者提出，儿童在进行有界NLE任务时，依赖于一种比例判断策略，有界NLE所测量的是个体的比例判断或比例推理的能力．比例判断策略是由Hollands和Dyre在研究个体如何进行比例估计时提出的，参与者被要求根据数线的左边界和右边界来估计目标值的位置[25]，例如，在0～100范围上估计50的位置，个体会将50转换为与整体的比例，即“50是100的一半，应该在0和100的正中间”，而不是使用整数估计策略直接对50这个数进行估计，认为“50就是0右边的50个单位”．Barth和Paladino首先提供了证明这一观点的系统证据，他们发现个体对位于参考点（如起点、中点和终点）附近的数值估计得更加准确，证明了有界NLE中个体所表现出来的估计模式确实反映了个体更熟练地使用越来越多的参考点，因而提出有界数线估计任务本质上就是一个比例判断任务，数线的端点显示出了其作为整体的价值[26]．还有一些研究也指出个体在完成有界NLE时会应用比例判断策略[27-29]．

为了克服有界数线在探究学生数字心理表征上的缺陷，使数线估计能够测量个体的量级表示能力，Cohen等提出了一个无界数线估计任务[24]．在无界NLE中，数线没有完整的端点，除了起点外还有一个单位距离（例如0到1这样一个单位距离），从这个单位距离开始，目标数必须位于给定的直线上（如图2）．参与者只能根据所给出的比例单位来估计目标数字的位置，这是为了防止参与者使用参考点和比例判断策略，使他们仅诉诸于量级估计．但Cohen等人发现，在无界NLE中，参与者倾向于使用另一种名为航位推算的策略，参与者首先在数线上移动一个单元，然后根据当前位置估计下一单元的位置，依此类推．实验数据表明，尽管有界NLE和无界NLE都用到了基本相同的数字认知结构，但无界NLE是一种更纯粹地测量个体数字表示的工具．

图2 无界数线估计任务

Cohen和Sarnecka比较了有界和无界数线估计任务发现，它们分别与不同的基本算术技能有关[30]．有界NLE需要参与者进行某种形式的减法或除法．个体通过估计与数线端点的距离，从而将目标数字放在数线上．为此，个体必须要能从数线上限的值中减去目标数字，例如，要将数字13放在从0～20范围的数线上，个体要能够从20中减去13，从而估计距离数字20左侧7个单位的位置．而在无界NLE中只需要加法，个体只需将给定的单位长度多次重复直至变成目标数字，即个体必须将13个单位长度相加，或者将单位长度乘以13．

3 数线估计的心理表征模式

已有研究常用数线估计任务探究儿童的数字估计．数字估计的核心问题是数字表征，个体在心理上如何表征数字体系体现了他们对数字的理解，也直接关系到数字估计的准确与否[31]．关于个体数字表征的模式，研究者持有多种看法，其中有一些具有代表性的表征模型．

3.1 线性模型与对数模型

线性模型（linear model）是Case等人提出来的，是指个体对所有数字的表征具有相等的心理空间距离，相邻数字之间的距离不会因数量的增加而改变[32-33]．该模型认为儿童的数字表征形式是线性的，但这种线性表征只有达到特定的年龄阶段才会出现．Case等人指出，不同年龄阶段的儿童会采用不同的表征，但特定年龄阶段的儿童只使用单一表征，6岁及以上年龄的儿童始终依赖于线性表征．只有掌握了线性表征，个体才能做到精确地估计．例如，4岁儿童无法准确估计两个个位数中哪个距离第三个数更近（譬如，3与8哪个距离6更近），他们仅仅能比较大小或多少，而6岁儿童一般都能进行精确估计，更大点的儿童则一直使用线性表征[34]．

Dehaene等人则在研究中发现，个体在表征数字时所采用的是一种对数模型（logarithmic model），个体在主观上认为1和2、2和4、4和8之间的空间距离是相等的．按照这种表征方式，对于某一范围内的数字，个体倾向于扩大低端数字间的距离，而缩小高端数字间的距离[35]．例如，对于0～1 000的数字范围，个体在心理上会认为1与75的距离比75与1 000的距离要大[31]．Dehaene等人通过对婴儿和动物的研究有力证明了这一模型的存在[36]，他们在对亚马逊地区没受过正规教育的Mundurucu土著居民的相关研究数据进行分析后发现，这些居民无论是儿童还是成人，对0～10的符号数和非符号数的表征都呈对数模式．而西方的成人只对较大的非符号数字采用对数表征，对较小的非符号数字和所有的符号数字均采用线性表征．这一结果表明：人类最初的表征形式是对数表征，线性表征是教育及文化的产物[37]．

3.2 对数—线性转换模型

Siegler等人考察了不同年龄段儿童数线估计的内部表征，提出了对数—线性转换模型（logarithmic-to-linear model）．Siegler等人提出了一种多重表征说，认为个体知道并能够使用多种数字表征方式，发展不是一种表征取代另一种，而是各种表征共存并竞争，不同的情境下会使用不同的表征模式，随着年龄和经验的增长，儿童会逐渐根据特定情境而依赖于最适合的表征．儿童对数字的心理表征最初呈不太准确的对数模式，而后逐步转化为更加准确的线性表征．这种从对数到线性的转换在多个数线估计的研究中被观察到[10，18，38]，且在不同的年龄段和数线的数值范围都有所呈现[6，8，39]．在1～100范围的数线估计任务中，大部分幼儿的估计结果与对数函数拟合；一年级的学生中大约有一半拟合对数函数，还有一半拟合线性函数；而二年级的学生大多符合线性函数．另外，对于同一年龄段，不同的数字估计范围也会有不同的表征，二年级学生在1～1 000范围的数线估计中，更加拟合对数函数．一些研究者将这一对数到线性转换的框架运用于描述数学学习障碍的要素[40-41]，以及探究数学终极起源的跨文化研究[37]当中．

3.3 线性—对数转换模型的质疑

一些研究者对于对数—线性模型并不认可．Ebersbach等人提出了一种分段线性模型（segmented linear model），他们认为在每个个体中可能只有一种表征，但这一表征至少由两个线性片段组成．在相对熟悉的数字范围内，个体能很好地进行线性估计和区分数字，表现为所呈现出的线性函数的斜率较大．一旦超过了熟悉的数字范围，估计仍然遵循线性曲线，但线性函数的斜率较小，表明在这个范围内，个体对数字位置的辨别能力较低[42]．Moller等人的研究也支持分段线性模型，但不同的是，Moller等人认为两条线性函数的分界点代表了从一位数到两位数的变化，而不是从熟悉的数字到不熟悉的数字，并推断随着年龄的增长和教育的影响，个体会逐渐转变为单一线性表征[21]．

Barth和Paladino也不赞同个体表征从对数到线性的转换，他们认为儿童估计准确性的线性增加可能只是反映了他们越来越熟练地应用比例判断策略，相比于大范围数字，个体在小范围数线上更容易准确利用参考点，更易呈现出线性表征．Barth等人指出，比例判断模型（proportion-judgment model）为个体的数字估计模式提供了一个很好的说明，特别是对儿童在NLE中所表现出的周期性偏差具有较好的解释力，而这种偏差是对数到线性表征模型或其它任何模型都无法解释的[26]．Slusser、Santiago和Barth发现，学前儿童无法使用中点作为参考，但随着儿童的发展，他们逐渐掌握通过参考点的位置来提高估计精确性的方法[43]．因此，他们认为儿童表征的发展可能是一个连续的过程，并不存在表征模式的转换．

儿童数字估计的心理表征发展引发了激烈争论，除上述数字心理表征模型外，还有研究者曾提出过独特的想法．比如Gibbon和Church所提出的存储器模型（accumulator model），将人的大脑比喻为存储器，数字以相等的空间距离被表征，表征数的过程像是数数的过程，也像是用杯子向存储器里倒水的过程，每数一个数便向存储器里倒一杯水，所数的最后一个数会存入记忆（存储器）中表征成主观量，当遇到目标数字时，这个量就会从记忆中被读出，读取的过程也是一个数数的过程[44]．这些表征模型大抵可以分为两类，即单一表征假说和多重表征假说．单一表征假说认为，个体在同一时期依靠单一规则进行数量表征，多重表征假说则认为，个体能根据具体情境采用不同的表征模式．

4 数线估计表现的影响因素

数线估计的表现受多种因素影响，把握这些因素，通过调节可控因素适当干预学生的数线估计，能够有效提高学生数线估计的准确性．

4.1 外在因素

Cohen和Sarnecka通过对比有界NLE和无界NLE的数据发现，儿童的表现只在有界数线上才会随着年龄的增长而发生显著变化，在无界数线上却相当稳定[30]．他们认为这是因为儿童面对不同类型的数线任务会采用不同的技能，最终导致NLE表现的变化．另外，数线上的数值范围也影响着儿童的NLE表现，Siegler和Opfer研究发现，二年级儿童估计的表征模式在0～100区间呈线性表征，而在 0～1 000区间呈对数表征[18]．Siegler等还对幼儿园和一年级儿童数线任务表现进行了探究，随着数字的增大，数字估计的准确性经历了一个由高变低，然后又逐渐变高的过程[6]．中国研究者分析了二年级儿童数线估计的数据，也得出随着数字范围扩大，估计的准确性降低的结论[45]．

Siegler等考察了美国中产阶级家庭与低收入家庭幼儿（平均年龄4.7岁）在0～10范围的NLE表现．与低收入家庭的幼儿相比，中产阶级家庭幼儿的估计数据更加接近线性函数[14]．Dehaene等人的跨文化研究发现，亚马逊地区的土著居民即便是成人，其数字估计依旧呈对数模型，这是由于他们缺乏系统的数学符号和正规的数学教育[37]．对中美幼儿园儿童的数线估计进行的跨文化研究结果指出，中国儿童在数线估计任务上的表现要优于美国同龄儿童[46]．周广东等人探讨了中国幼儿园和小学儿童数字估计能力的发展，并与Siegler等人对美国儿童的研究做了对比，发现在0～100范围上，中国儿童在一年级就能进行较为精确的估计，而美国儿童在二年级才达到相似水平；在0～1 000范围上中国儿童的估计在三年级时就较为精确了，相比之下美国六年级儿童才能对该范围的数字进行精确估计[31]．

4.2 内在因素

Geary对数学学习困难、学业成就低和正常儿童的数字估计能力的追踪研究发现，数学学习困难和低数学成绩的儿童估计准确性显著低于正常儿童[41]．Fanari等人通过使用符号和非符号知识任务研究发现，涉及符号知识的任务对NLE表现差异的解释力较高，而非符号数字知识任务并不能预测NLE的表现，因此得出5岁幼儿在NLE上的表现取决于符号知识的结论[47]．对于幼儿来说，数数能力是一个主要的影响因素．较小的儿童会使用数数策略去解决数线估计问题，他们或是从最小值往后数，或是从最大值往前数，又或是从中间的值往两端数．而对于稍微年长一点的儿童和成人，有关比例的知识会使得他们在数线估计中表现较好．例如，六年级儿童和成人在进行0～1 000范围的数线估计时，相较于其它数字，他们对处于0、250、500、750、1 000附近的数字的估计显然要准确得多[18]．这表明个体能够依据特殊的参考点如有界数线的端点、中点等，在心理上把数线平均分成若干等分，以其中的一份为基准展开对数字的估计．刘国芳等人也考察了5～6岁幼儿在0～100范围的数线估计表现，结果发现幼儿是一个“灵活的策略使用者”，他们倾向于使用中点和端点策略进行数线估计[48]．邢强等人对二、四、六年级的学生在0～100范围的数线估计表现进行了分析，结果发现3个年级的学生都对数字50的估计明显要准于其它数字，说明他们在估计中准确运用了分半策略[38]．

Siegler提出反馈是一种有效的改善NLE表现的方式，个体一旦获得了有关精确表征的经验就会放弃旧的表征形式，选择新的表征形式，且这种变化是突然的、整体性的，无论延时反馈还是实时反馈都能显著影响后续儿童数线估计的准确性[6]．李晓芹考察了中国小学儿童的NLE表现，得出结论：相比于无反馈组，反馈组儿童估计的准确性会得到显著提高[49]．莫雷等人提出“心理长度”的概念，是指儿童将低端数字与固定的线段长度对应起来的特点．莫雷等人认为，年幼儿童数字估计之所以呈对数模式，并不是他们真正在运用对数策略进行数字估计，而是由于他们在一定长度数字线范围内对低端的数字有着对应的固定不变的心理长度，这种对应关系不会随着数字范围及数线长度的变化而变化．心理长度的存在反应了儿童对数的等距属性的认识，在没有发展到认识等比属性之前，真正的线性表征是不可能出现的．因此，心理长度是导致儿童在不同数字范围下产生不同表现的根本原因[50]．

5 数线估计的教学意蕴

从上述内容可知，有界NLE和无界NLE对学生不同的数学能力提出了要求，利用相关因素可以改善儿童数线估计表现进而促进其数学能力的提升．由此可见，数线估计具有一定的教学意义，不失为教学的良好辅助工具．结合当前已有研究内容来看，数线估计的教学运用主要存在小学数学的“数与代数”领域，教师若能在教学过程中寻找合适的时机加以利用，或许会对学生的数学学习和早期数学能力发展起到一定的促进作用．

5.1 运用无界NLE丰富识数计数教学以发展学生的数感

数感的良好发展是形成数学核心素养的前提[51]．数感的发展，需要经历感悟多少、用数表示多少、建立数之间的关联、对数进行运算、形成数系概念等过程．学生用数表示多少的第一步是数数，通过数数可以抽象出数与数之间的关系，如大小、顺序、分解与组合等[52]，从而建立数的概念．数的概念的建立并非一蹴而就，学生理解和掌握数的概念需要经历一个循序渐进的过程[53]．小学低年级是培养数感的重要时期，识数、计数是发展低年级学生数感的重要途径．但对低年级学生来说，他们对数的理解尚未达到抽象水平，还需要依托具体实物来认识数和理解数．数线就是一个很好的辅助学生认识数的实体工具．以一年级教材为例，“认识10以内的数”单元就可使用数线估计辅助教学．

认识数字1～9时，教师可以先采用具体情境中的数量如小圆片、小棒等，再过渡到数字表达，让学生体验1～9的从数量到数的抽象过程．系统认识了1～9之后可以引入数线，让学生自行在数线上表示出各个数字所在的位置或是填出数线上缺少的数（如图3），这一过程将学生脑中抽象的数又转化为数线上具体有形的数，加深对数字的认识．在之前识数的过程中，学生已经感受到数字是有序排列的，利用数线表示数能够加深对数字有序性的认识以及对数字顺序与数字大小二者之间关系的体验．

图3 运用无界数线识数

在学生基本熟悉了数字在数线上的表示后，引入无界NLE，让学生估计某个数在无界数线上的位置，发展学生对数的等距属性的认识．五年级初步认识负数以后，无界数线及无界NLE还可以拓展到负数领域（如图4）．另外，无界数线并没有固定的长度，因而具有一定的开放性，教师可以使用无界数线让学生直观感受到随着数线往右（左）无限延伸，数字是可以无限增加（减小）的．教师可以在学生认识完20以内的数后将其作为拓展，为后续认识百以内、万以内的数甚至更大的数埋下伏笔．在感受数字系统的无限性的过程中发展学生的空间想象力，培养学生数形结合的数学思想方法．

图4 运用无界数线认识负数

学生在小学低年级阶段学习的数学概念与计数有密切联系．通过真实的计数经验，学生发展基本概念和策略，帮助他们理解和描述数字，发现数字之间的关系和模式[54]．无界NLE需要依靠加法完成，学生在无界数线上进行估计时需要将所给出的单位距离逐步累加至目标数字，在这一过程中产生计数的操作．在教学1～5的加减法之前，教师可以采用无界数线估计任务，先发展学生的计数经验，让学生有“在一个数上加上1”的意识，为后续加减法教学打下基础．还可以使无界数线以“2”“3”等数字为初始单位距离，从“在一个数上加1”变成“在一个数上加2”“在一个数上加3”等，以多种形式丰富学生的计数经验．例如，在初始单位为1的无界数线上分别估计数字2和5的位置，学生需要分别将单位距离累加1次和4次，依托具体实物完整经历抽象的计数过程．学生在累加时教师要引导其注意保持每个单位距离是相同的，它们是代表相等大小的“1”．最终结果呈现以后，教师可以让学生比较两次无界数线估计的结果，发现线的长度不同，同时可以引导学生在2的后面补上3段一样的单位距离就能够和5一样长（如图5），以将抽象数字变具象的方式使学生加深对数字大小的认识和对量的大小的体验，发展学生的数感与量感．

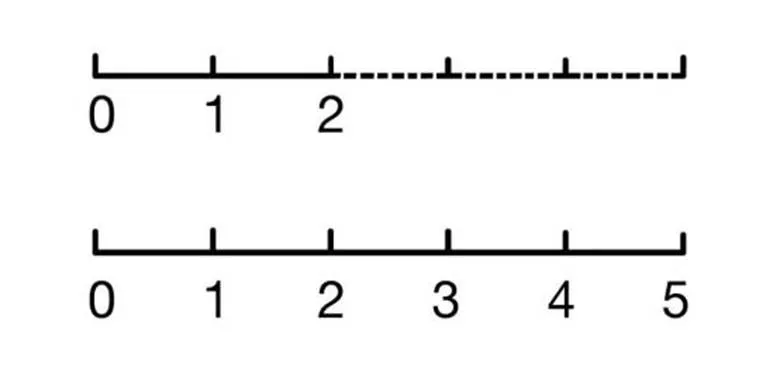
图5 在无界数线上分别估计2和5的位置

5.2 运用有界NLE辅助比例知识教学以发展学生的比例 推理能力

数学推理作为一种基本思维方式贯穿了数学学习活动的全过程．不同的学习内容，数学推理的表现形式也有所不同[55]．在学校数学教学中，比例推理是一种常见的数学推理，它主要基于比和比例知识的学习．比是对数量的倍数关系的一种刻画[56]．比例推理是关于数量关系的思考，是基于比和比例知识进行推理的一种能力[57]，要求同时对几个数量或值做出比较[58]，也是根据已知信息和比例的相关性质进行判断和计算的思维过程[59]，要基于具体情境把握其中的数量关系变化．比例推理能力的发展对学生数学推理能力的发展至关重要．

小学阶段，涉及比例推理的内容主要包括数与代数领域中的“正比例、反比例”以及“路程=速度×时间”等数量关系的建构[55]．但实际上，小学数学课程的许多部分都直接或间接涉及到比，例如分数、百分数、概率等，可以说比例推理贯穿小学数学的始终[60]，对于更高层次的数学理解必不可少．因此在小学低年级就可以考虑将比例推理的思想融入数学教学，逐步培养儿童的比例推理思维，发展比例推理能力．比例推理的发展是一个渐进的过程，其基础是日益复杂的乘法思维和比较两个量的相对而非绝对大小的能力．有界NLE其实属于Lamon所划分的比例推理类问题中的“部分—整体”型问题[61]，它对相对思维提出了要求，学生需要把握数字之间的相对大小关系才能进行准确估计．在教学中，有界NLE可以在正式学习比的相关知识之前呈现给学生，学生在估计时可能会参照中点、四分之一位点等参考点的位置，实际上就是在比较数字之间的关系．例如，在0～100的数线上估计23的位置，学生可能会先将20转化为在整体中所占的比重即“100的五分之一”，进而标记在数线的五分之一处往右一点．这一过程初步启发了学生的比例推理思维．

除了有界NLE能够帮助学生发展比例推理能力，双数线也是一种培养学生比例推理意识的直观手段．由于比涉及两个量之间的关系，在教学中利用双数线可以向学生直观展现两个量之间的共变，发展学生的比例推理意识．双数线可以在学习比的相关知识之后，在练习题中作为解题的辅助工具引入．例如，要求写出等式中的缺失值8∶5=32∶（ ），教师可以在双数线上标出已知的三个数，并将其对应（如图6），以直观的方式让学生感知这两个量之间存在着的共变关系．此时，教师要让学生明白，这两条线可以无限延长，它们的比也可以写出无限多对，但存在一个最简整数比．类似地，还可以换成实际问题．例如：用13个梨可以换2个西瓜，那用6个西瓜可以换几个梨？

图6 运用双数线进行比例推理

由于比和分数存在密切联系，有界NLE对分数教学也有一定意义．小学阶段最为注重数与运算的表征，尤其是对分数概念与运算的表征[62]．分数具有多重意义[63]，其表征形式也复杂多样．不同于一些图象表征可能造成的“分数是两个整数的组合”的认知偏向，有界NLE在保留直观性的前提下又增加了适当的抽象性，在一定程度上帮助理解分数的部分—整体意义的同时，又可以避免“整数偏向”[64]，帮助学生过渡到对分数的度量意义的理解，从而将分数看成是一个数．另外，还有研究发现：在早期阶段，直接比较和非标准测量是儿童测量能力的主要表现形式，其中非标准测量是指用自然物形成的非标准测量单位对物体进行比较衡量[65]．而有界NLE所使用的是标准单位，给定线段长度，数量大小要与固定的长度相对应．因此，使用有界NLE还能够帮助学生从早期的非标准测量逐步过渡到标准测量，发展基础的标准测量能力．

5.3 运用NLE进行教学评价以促进学生早期数学能力的发展

数线估计是数字估计研究中常用的研究范式，它能衡量学生的数字认知等一系列数学能力．利用这一点，可以将其作为一种教学评价工具．譬如，对一年级学生而言，教师可以利用数线估计编制小测验用以评估入学新生的数字认知状况，以便把握学生的现有水平，有针对性地展开教学，这有助于做好幼小衔接工作．在之后认识10以内的数、11～20各数、100以内的数这样一个阶段的学习结束后，均可利用数线估计测量学生已达到的数字认知水平，及时获得教学结果的反馈．如此，NLE在认识数的教学中的使用或许可以形成一个流程：利用NLE进行前测—借助NLE辅助数的认识和加减教学—利用NLE进行后测．

数线估计的准确性越高预示着个体在数学上有更高的成就．一方面，个体在头脑中如何表征数字会影响其数线估计的准确性．从准确性角度来说，对数表征是儿童对数字的一种不精确表征，而线性表征则是比较理想的表征方式，个体的估计模式越接近线性其估计结果越准确．然而，线性表征并非是个体生来就有的，个体最初似乎更倾向于不太准确的对数表征．因此，为引导学生的表征模式向着更为准确的线性模式发展，改善学生的数线估计表现，促进学生数字估计能力的发展，教师可以对学生的数线估计进行适当干预．教师要对学生的数线估计结果予以及时反馈，反馈能够引发学生的认知冲突，是一种矫正偏差的有效方式，特别是在学生出现较大的估计偏差时．得到对估计结果的反馈后，学生会修正或坚持自己最初的估计以提高之后估计的准确性，从而逐步向线性表征发展．

另一方面，个体数线估计的准确性会随着年龄的增长而提高，到达一定年龄后估计的准确性才会趋于稳定，在这一过程中还会产生个体差异，部分学生可能相对发展较为缓慢．因此，在儿童发展早期，教师可以采取一些游戏训练促进他们对数字的认知．例如，教师可以让学生进行数字分类．数字分类是指让儿童基于数量对数字形成主观的大小分类，比如“非常小”“小”“中”“大”“非常大”这些类别．Laski等通过让儿童对数字进行分类，再进行数线估计任务训练，最终发现对儿童数字分类的训练能够有效提高数线估计的准确性[20]．教师可以将数字做成一张张小卡片，利用课间或课前准备时间，与学生进行分类小游戏，学生分类后教师要给予反馈，反馈不仅会提高他们在数字分类方面的水平，而且会提高他们在其它数字认知方面的水平[41]．教师还可以开展数字棋盘游戏以促进学生对数字的理解．常见的是线性数字棋盘，是指具有连续编号、呈线性排列、空间大小相同、颜色相间隔的方格棋盘，棋盘上印有数字0～99，本质上是物化了的数线．儿童通过掷骰子的点数确定棋子要移动的格数，一边移动棋子一边要说出所走过的数[14]．有研究者指出，数字棋游戏能提高儿童数数和识数的水平，提高儿童对数字顺序和数量大小的认知能力[66]．

数线是体现数形结合思想的数学实体，既是数学学习的内容，也是数学教学的有效辅助工具；数线估计是依据数线特点所设计的数学学习任务或情景，既可以有效地辅助学生学习数学，也可以帮助教师判断甚至诊断学生数学学习结果的成效或成因．尽管数线及数线估计似乎相对简单，且其运用于教学的效果可能无法立刻显现出来，但其潜在的价值如对学生数感萌芽的促进是不可估量的，教师若能在小学低年级运用好数线和数线估计或许会有效促进学生早期的数字认知以及其它数学能力的发展．

[1] 黄继蓉，陈光喜，黄文韬．多媒体技术与数学“数形结合”教学[J]．数学教育学报，2009，18（2）：76–78．

[2] WONG M. Identifying fractions on a number line [J]. Australian Primary Mathematics Classroom, 2013, 18 (3): 13–18.

[3] ORRILL C, BROWN R. Making sense of double number lines in professional development: Exploring teachers’ understandings of proportional relationships [J]. Journal of Mathematics Teacher Education, 2012, 15 (5): 381–403.

[4] IANNONE P. Number tracks, number lines, number strips…Are they all the same [J]. Mathematics Teaching, 2006 (197): 9–12.

[5] 许晓晖．儿童数字估计能力的研究进展及其启示[J]．首都师范大学学报（社会科学版），2015（3）：148–155．

[6] SIEGLER R S, BOOTH J L. Development of numerical estimation in young children [J]. Child Development, 2004, 75 (2): 428–444.

[7] LAI M, ZAX A, BARTH H. Digit identity influences numerical estimation in children and adults [J]. Developmental Science, 2018, 21 (5): 1.

[8] BOOTH J L, SIEGLER R S. Developmental and individual differences in pure numerical estimation [J]. Developmental Psychology, 2006, 42 (1): 189–201.

[9] BOOTH J L, SIEGLER R S. Numerical magnitude representations influence arithmetic learning [J]. Child Development, 2008, 79 (4): 1 016–1 031.

[10] 宋广文，李晓芹，朱振菁．小学儿童数字线估计的心理表征模式[J]．数学教育学报，2013，22（5）：52–56．

[11] MIX K S, CHENG Y L. The relation between space and math: Developmental and educational implications [J]. Advances in Child Development and Behavior, 2012 (42): 197–243.

[12] CHENG Y L, MIX K S. Spatial training improves children’s mathematics ability [J]. Journal of Cognition and Development, 2014, 15 (1): 2–11.

[13] 李梦霞，郑杨玲．感知—运动空间训练对儿童早期数学能力的影响[J]．数学教育学报，2022，31（3）：56–63，102．

[14] SIEGLER R S，RAMANI G B. Playing linear numerical board games promotes low-income children’s numerical development [J]. Development Science, 2008, 11 (5): 655–661.

[15] RAMANI G B, SIEGLER R S. Reducing the gap in numerical knowledge between low- and middle-income preschoolers [J]. Journal of Applied Developmental Psychology, 2011 (32): 146–159.

[16] FISCHER U, MOELLER K, BIENTZLE M, et al. Sensori-motor spatial training of number magnitude representation [J]. Psychonomic Bulletin & Review, 2011, 18 (1): 177–183.

[17] 黄大庆，陈英和．小学二至六年级数学困难儿童数学认知能力的发展[J]．数学教育学报，2016，25（2）：70–74．

[18] SIEGLER R S，OPFER J E. The development of numerical estimation: Evidence for multiple representations of numerical quantity [J]. Psychological Science, 2003, 14 (3): 237–243.

[19] 张帆，赖颖慧，陈英和．儿童数字线表征的发展——心理长度的影响[J]．心理发展与教育，2015，31（2）：149–156．

[20] LASKI E V, SIEGLER R S. Is 27 a big number? Correlational and causal connections among numerical categorization, number line estimation, and numerical magnitude comparison [J]. Child Development, 2007, 78 (6): 1 723–1 743.

[21] MOELLER K, PIXNER S, KAUFMANN L, et al. Children’s early mental number line: Logarithmic or rather decomposed linear [J]. Journal of Experimental Child Psychology, 2009, 103 (4): 503–515.

[22] BERTELETTI I, LUCANGELI D, PIAZZA M, et al. Numerical estimation in preschoolers [J]. Developmental Psychology, 2010, 46 (2): 545–551.

[23] OPFER J E, THOMPSON C A, KIM D. Free versus anchored numerical estimation: A unified approach [J]. Cognition, 2016 (149): 11–17.

[24] COHEN D J, BLANC-GOLDHAMMER D. Numerical bias in bounded and unbounded number line tasks [J]. Psychonomic Bulletin and Review, 2011, 18 (2): 331–338.

[25] HOLLANDS J G, DYRE B P. Bias in proportion judgments: The cyclical power model [J]. Psychological Review, 2000, 107 (3): 500–524.

[26] BARTH H C, PALADINO A M. The development of numerical estimation: Evidence against a representational shift [J]. Developmental Science, 2011, 14 (1): 125–135.

[27] ASHCRAFT M H, MOORE A M. Cognitive processes of numerical estimation in children [J]. Journal of Experimental Child Psychology, 2012, 111 (2): 246–267.

[28] DACKERMAN T, KROEMER L, NUERK H C, et al. Influences of presentation format and task instruction on children’s number line estimation [J]. Cognitive Development, 2018 (47): 53–62.

[29] COHEN D J, QUINLAN P T. The log-linear response function of the bounded number-line task is unrelated to the psychological representation of quantity [J]. Psychonomic Bulletin & Review, 2018, 25 (1): 447–454.

[30] COHEN D J, SARNECKA B W. Children’s number-line estimation shows development of measurement skills (not number representations) [J]. Developmental Psychology, 2014, 50 (6): 1 640–1 652.

[31] 周广东，莫雷，温红博．儿童数字估计的表征模式与发展[J]．心理发展与教育，2009，25（4）：21–29．

[32] CASE R, SOWDER J T. The development of computational estimation: A neo-piagetian analysis [J]. Cognition and Instruction, 1990, 7 (2): 79–104.

[33] BRANNON E M, WUSTHOFF C J, GALLISTEL C R, et al. Numerical subtraction in the pigeon: Evidence for a linear subjective number scale [J]. Psychological Science, 2001, 12 (3): 238–243.

[34] CASE R, OKAMOTO Y. The role of conceptual structures in the development of children’s thought [J]. Monographs of the Society for Research in Child Development, 1996, 61 (1–2): 1–265.

[35] DEHAENE S. The number sense: How the mind creates mathematics [M]. New York: Oxford University Press, 1997: 73–78.

[36] DEHAENE S, DEHAENE-LAMBERTZ G, COHEN L. Abstract representations of numbers in the animal and human brain [J]. Trends in Neuroscience, 1998, 21 (8): 355–361.

[37] DEHAENE S, IZARD V, SPELKE E, et al. Log or linear? Distinct intuitions of the number scale in western and amazonian indigene cultures [J]. Science, 2008, 320 (5 880): 1 217–1 220.

[38] 邢强，徐争鸣，蔡新华．小学生数字线估计中的分段策略[J]．数学教育学报，2015，24（4）：82–87．

[39] OPFER J E, SIEGLER R S. Representational change and children’s numerical estimation [J]. Cognitive Psychology, 2007, 55 (3): 169–195.

[40] GEARY D C, HOARD M K, BYRD-CRAVEN J, et al. Cognitive mechanisms underlying achievement deficits in children with mathematical learning disability [J]. Child Development, 2007, 78 (4): 1 343–1 359.

[41] GEARY D C, HOARD M K, NUGENT L, et al. Development of number line representations in children with mathematical learning disability [J]. Developmental Neuropsychology, 2008, 33 (3): 277–299.

[42] EBERSBACH M, LUWEL K, FRICK A, et al. The relationship between the shape of the mental number line and familiarity with numbers in 5- to 9-year old children: Evidence for a segmented linear model [J]. Journal of Experimental Child Psychology, 2008, 99 (1): 1–17.

[43] SLUSSER E B, SANTIAGO R T, BARTH H C. Developmental change in numerical estimation [J]. Journal of Experimental Psychology General, 2013, 142 (1): 193–208.

[44] GIBBON J, CHURCH R M. Time left: Linear versus logarithmic subjective time [J]. Journal of the Experimental Analysis of Behavior, 1981 (7): 87–107.

[45] 曹碧华，曾春雲，廖虹，等．心理长度对二年级儿童数字线估计表征的影响[J]．心理发展与教育，2021，37（2）：190–198．

[46] SIEGLER R S, MU Y. Chinese children excel on novel mathematics problems even before elementary school [J]. Psychological Science, 2008, 19 (8): 759–763.

[47] FANARI R, MELONI C, MASSIDDA D. Early numerical competence and number line task performance in kindergarteners [R]. The International Association for Development of the Information Society (IADIS) International Conference on 14th Cognition and Exploratory Learning in Digital Age. Algarve, 2017–10–18.

[48] 刘国芳，辛自强．数字线估计研究：“模型”背后的策略[J]．心理研究，2012，5（2）：27–33．

[49] 李晓芹．小学儿童数字线估计的发展研究[D]．曲阜：曲阜师范大学，2008：48．

[50] 莫雷，周广东，温红博．儿童数字估计中的心理长度[J]．心理学报，2010，42（5）：569–580．

[51] 孙虎，张伟平，陈志辉，等．基于核心素养的六年级学生数感现状调查研究[J]．数学教育学报，2021，30（4）：41–47．

[52] 史宁中，吕世虎．对数感及其教学的思考[J]．数学教育学报，2006，5（2）：9–11．

[53] 马云鹏，史炳星．认识数感与发展数感[J]．数学教育学报，2002，11（2）：46–49．

[54] 张文宇，宋军．加拿大小学数学课程标准中的数感与运算能力评析——以安大略省为例[J]．数学教育学报，2016，25（3）：38–43．

[55] 张侨平，邢佳立，金轩竹．小学数学教学中数学推理的理论和实践[J]．数学教育学报，2021，30（5）：1–7．

[56] 朱立明，马云鹏．小学数学中“除法”“分数”与“比”的辨析与思考[J]．数学教育学报，2020，29（5）：32–35．

[57] 李晓东，蔡梦婕，江荣焕．克服比例推理的过度使用——抑制控制与工作记忆的视角[J]．数学教育学报，2021，30（3）：73–77．

[58] 李晓东，江荣焕，钱玉娟．中小学生对比例推理的过度使用[J]．数学教育学报，2014，23（6）：73–77．

[59] 巩子坤，杨婷，张都，等．三～六年级学生分数概念的错误理解及其发展[J]．数学教育学报，2021，30（5）：14–20．

[60] 巩子坤，程玲，陈影杰．小学生比例推理学习进阶模型的构建[J]．数学教育学报，2022，31（5）：48–53，64．

[61] LAMON S J. Ratio and proportion: Connecting content and children’s thinking [J]. Journal for Research in Mathematics Education, 1993, 24 (1): 41–61.

[62] 沈阳，张晋宇，鲍建生．表征在数学教育中的研究现状[J]．数学教育学报，2022，31（2）：82–89．

[63] 赵莉，王春英，史宁中．分数概念表述和分数除法运算的比较研究及其对教学的启示[J]．数学教育学报，2021，30（3）：46–51．

[64] 丁锐，卫冰倩，RON T，等．分数度量意义发展的认知根基及轨迹：分数图式进阶理论[J]．数学教育学报，2021，30（3）：64–72．

[65] 张华，庞丽娟，陶沙，等．儿童早期数学认知能力的结构及其特点[J]．心理学报，2003（6）：810–817．

[66] 白璐．5～6岁儿童数字估计能力的干预研究[D]．北京：首都师范大学，2014：60–63．

Number Line Estimation and Its Teaching Implications

XU Yu-man, LU Shi-qi, XU Wen-bin

(Curriculum and Teaching Institute, Nanjing Normal University, Jiangsu Nanjing 210097, China)

Number Line Estimation is an important tool for measuring and predicting children’s mathematical abilities. Children’s performance on NLE reflects their understanding of numbers; higher NLE accuracy indicates greater achievements in children’s mathematics. Studies have shown that there are two types of NLE, bounded NLE and unbounded NLE. Models for individual representation of numbers include linear representation model, logarithmic representation model and so on. The factors influencing NLE performance include external factors such as different types andnumericalranges of NLE, family economic status, culture and education, and internal factors such as individual mathematical cognitive abilities and cognitive processing. Combining the characteristics of number lines and NLE, teachers can use it as a tool to assist students in learning. For example, teachers can develop students’ number sense by using unbounded NLE, develop students’ reasoning and measuring ability by using bounded NLE to assist students’ proportional knowledge learning, and promote the development of students’ mathematical cognition and other mathematical abilities.

number line; number line estimation; numerical mental representation; influencing factors; teaching implications

G622.4

A

1004–9894（2023）05–0068–08

徐玉嫚，陆世奇，徐文彬．数线估计及其教学意蕴[J]．数学教育学报，2023，32（5）：68-75．

2023–07–07

安徽省高校协同创新项目——“双减”背景下教学和谐的理论证成、实践省察与行动构建（GXXT-2021-058）

徐玉嫚（1998—），女，江苏盐城人，硕士生，主要从事小学数学教学研究．

[责任编校：陈汉君、张楠]