结合放射线法和无人机影像提取冠幅估算杉木碳储量研究
王杰芬,夏磊,林露花,胡璐璐,徐怀兴,王聚中,徐小军
(1. 浙江省龙泉市林业局,浙江 龙泉 323700;2. 浙江农林大学 环境与资源学院,浙江 杭州 311300)
全球气候变化给人类生产和发展带来巨大的影响,开展森林碳循环研究对减缓气候变化具有重要意义。森林生态系统是陆地生态系统中最大的碳库,其年固碳量占整个陆地生态系统年固碳量的2/3,具有很强的碳储存能力[1]。我国森林年固碳量约为4.34 亿t,人工林对我国森林碳库持续增长起到重要的作用[2],尤其是杉木Cunninghamialanceolata人工林种植面积大、分布范围广,其碳储量约为3.03 亿t,位居前列[3]。因此,开展杉木碳储量估算研究,有利于准确掌握杉木碳储量现状和动态变化,对提升杉木林碳储量和固碳潜力具有重要的意义。
目前,森林碳储量估算的方法主要包括生物量法、模型模拟法和遥感估算法等[4-5]。通过树高、胸径等测树因子建立异速生长方程估算碳储量,是最常用的方法。Mei 等用胸径、树高和木材密度建立了杉木个体生物量模型,对福建将乐国有林场的杉木林分进行了生物量估算[6]。庄红蕾等用异速生长方程法对崇明岛水杉Metasequoiaglyptostroboides幼龄林、中龄林和成熟林进行了碳储量估算,取得较高的精度[7]。但通过样地调查方法获取树高、冠幅和胸径等测树因子构建异速生长方程,不仅费时费力、效率低,而且难以大面积应用[8]。随着无人机遥感技术的发展和普及,为树高、冠幅和胸径等参数的获取提供了新方法[9]。徐永胜等用改进的分水岭分割算法提取单木冠幅和树冠投影面积,精度分别为79.84%和76.04%[10]。王越等采用无人机倾斜摄影测量技术构建三维模型,进而提取树高和冠幅[11]。谢巧雅等利用无人机影像构建数字表面模型和数字高程模型,通过两者相减,从而提取杉木树高,精度达90.8%[12]。但是,对于郁闭度较大的林分,地面信息获取难度很大,难以获取精准的数字地形模型,造成树高提取误差大[13]。另一方面,树高提取通常需要单木树冠顶点信息,当树冠顶点提取存在偏差时,会导致树高低估的现象[12]。因此,通过无人机可见光影像提取山区高郁闭度林分树高仍然存在较大的不确定性。冠幅信息在无人机可见光影像中能够得到直观的反映,且与树高和胸径有较强的相关性,冠幅越大,胸径也越大[14-16]。张玉薇等将提取的冠幅和树冠面积与胸径建立回归模型,能够准确地估算胸径,相对误差低于5%[17]。贾鹏刚等采用无人机影像提取银杏Gingkobiloba单木树冠面积、冠幅和树高三个因子可较高精度地估算出胸径,精度满足森林资源调查要求[18]。Gonzalez-Benecke 等研究得出树冠面积对提高单木胸径和蓄积估算精度起到重要作用[15]。因此,以冠幅为自变量,可较准确地估算单木胸径,为基于无人机影像估算单木和林分水平杉木碳储量提供可行性。
浙江省是杉木主要分布省份,丽水市是浙江省杉木主要分布区域。本研究借助大疆无人机M300 获取可见光影像,对影像进行正射校正后,采用放射线法提取单木冠幅,并对冠幅进行精度验证,然后,建立冠幅与胸径以及胸径和树高之间的回归模型,估算出胸径和树高;最后,将树高和胸径代入杉木碳储量异速生长模型,估算出单木和林分水平碳储量,并进行精度评价。本研究成果将验证基于无人机影像提取的冠幅信息在估算杉木胸径、树高以及单木和林分水平碳储量上的可行性,为快速准确估算杉木林碳储量提供技术和方法支撑。
1 数据与方法
1.1 研究区概况
研究区位于浙江省西南部的丽水龙泉市,地理坐标为27°42' ~ 28°20' N,118°42' ~ 119°25' E,东西长为70.25 km,南北宽为70.80 km,总面积为 304 486 hm2。属中亚热带季风气候区,四季分明、雨量充沛、温暖湿润。全市森林资源丰富,以针叶林、阔叶林、针阔混交林为主,林业用地面积为 26.6 万hm2,活立木总蓄积量为1 987 万m3,森林覆盖率高达84.38%,位居浙江省前列[20]。全市杉木林面积为11.15 万hm2,平均蓄积量为 97 m3·hm-2[19]。
1.2 样地调查数据获取
在龙泉市查田镇和八都镇分别选择1 个杉木纯林样地,林地面积分别为774.2 m2和920.4 m2。样地1 位于查田镇,地理坐标为118°57'56.8'' E,27°53'11.4'' N,为18 年生人工中龄林,初植密度为3 300 株·hm-2。样地2位于八都镇,地理坐标为118°57'18.8'' E,27°59'33.7'' N,为27 年生人工成熟林,初植密度为2 700 株·hm-2。2个样地均开展间伐抚育、割灌除草、除藤等经营措施。样地1 和样地2 的坡度分别为12°和5°。采用十步抬头法,沿样地两条对角线记录被枝叶遮挡次数,计算样地1 和样地2 杉木林冠层郁闭度分别为0.8 和0.4。样地1林下以土壤、枯枝为主,有少量蕨类植物;样地2 林下植被茂密,覆被灌木、蕨类和草本植物。样地大小参考浙江省森林资源连续清查标准样地(28.28 m×28.28 m)[20],并将样地划分为9 个小样方。为了能够在无人机影像中准确地找出每个小样方的位置,在每个小样方角点上竖立标杆,标杆上放置易识别的红布。由于小样方角点被杉木遮挡,导致在无人机上无法识别,因此将标杆移至距离小样方角点最近的林窗内,最终,将每个大样地划分为9 个不规则小样方(图1)。记录每个小样方内的每株杉木坐标并绘制杉木分布图。对样地内的杉木进行每木检尺,起测径阶为5 cm,调查样地内每棵杉木的胸径和冠幅等。另外,从森林资源二类调查数据中获取查田镇和八都镇杉木小班平均胸径和平均树高,查田镇有1 016 个杉木小班,八都镇有1 360 个杉木小班,用于构建树高和胸径关系式。

图1 样地和杉木分布图Fig. 1 Sample plots and distribution of C. lanceolata
1.3 无人机影像获取
2022 年2 月,选择晴朗无风天气,使用大疆无人机M300 搭载的禅思H20T 可见光传感器获取影像数据,航拍高度设置为100 m。样地1 拍摄时间在11:20—11:40,样地2 拍摄时间在09:50—10:10。在2 个样地分别拍摄16 张单幅影像,然后将无人机单幅影像导入Agisoft PhotoScan Pro 软件做拼接和正射校正处理,生成正射影像,影像的空间分辨率为3.48 cm·pixel-1。
1.4 基于放射线法提取冠幅
放射线法是单木冠幅估计的一种常用方法,该方法以树冠中心点为起点,向四周发射射线,根据树冠中心点亮度值大于树冠边缘点亮度值的前提假设,即由中心点向四周延伸的射线经过的像元亮度值呈递减的趋势,并且在树冠边缘处递减的梯度最大,因此可以通过对射线亮度值曲线做多项式拟合平滑处理,然后找出平滑后曲线亮度值变化最大处所对应的位置,即为树冠的边缘点,计算各边缘点到树冠中心点的距离就可得到冠幅[21]。本文基于放射线法的原理,在找寻树冠边缘点时,将各个方向射线上亮度值最小且与树冠中心点距离最近的像元作为树冠边缘,并且加入了树冠边缘点位置调整系数(α)以及各射线冠幅估计值异常值剔除百分数(β),来提高单木冠幅估算精度。具体步骤如下:
(1)以树冠中心点(通过目视解译方法获取)为中心,以N为窗口大小,构建一个N×N大小的窗口。以窗口左上角像元为起点,依次按顺时针方向提取经过树冠中心点的射线。对于一个N×N的窗口,共有2×N-2 条射线。窗口越大,射线数量越多,N通常稍大于影像中树冠冠幅最大值。
(2)依次提取出各射线的特征曲线(亮度值)并进行平滑处理。找出特征曲线的最大值及其对应的像元,以该像元为分割点,分别搜索分割点两边离分割点最近的最小亮度值。然后,分别计算分割点两边亮度值的变幅,即最大值与最小值之差,查找两边亮度值与α×变幅+最小值最接近的像元,记为左侧边缘点和右侧边缘点,然后计算出左侧边缘点和右侧边缘点之间的距离,即为该射线得到的冠幅估计值。依次计算出每条射线的冠幅估计值。
(3)为了剔除由于树冠内大孔隙背景、树冠周边相似背景以及树冠重叠等原因造成的过小或过大的冠幅估计值,计算出所有射线冠幅估计值的百分位数β和100-β对应的冠幅估计值CLβ和CL100-β,取冠幅估计值位于CLβ与CL100-β之间的数值,并取均值作为最终的单木冠幅估计值。
1.5 杉木碳储量估算
首先,根据样地调查中实测的378 棵杉木胸径和冠幅数据,建立胸径和冠幅回归模型;其次,根据小班杉木平均胸径和平均树高数据,建立胸径和树高回归模型;然后,将基于无人机提取的冠幅值代入胸径和冠幅回归模型,得到胸径估计值,将胸径估计值代入胸径和树高回归模型,得到树高估计值;最后,将胸径和树高估计值代入杉木全株碳储量相对生长模型,计算出样地内每棵杉木的碳储量。杉木全株生物量相对生长模型采用由刘雯雯等构建的区域尺度杉木生物量通用相对生长方程,见式(1)[22]。该方程适用胸径和树高范围广、通用性强,决定系数(R2)为0.93。杉木生物量转换为碳储量的系数为0.5[23-24]。
式中,W为全株生物量;D和H分别为胸径和树高。
1.6 精度评价
根据每棵杉木的坐标及绘制的杉木位置分布图,在无人机影像中标记出每棵杉木,确保每棵杉木实测冠幅与无人机影像提取冠幅一一对应。采用实测的冠幅对无人机影像提取的冠幅进行精度评价。采用样地实测胸径对胸径估计值进行精度评价。将实测胸径和树高估计值代入杉木碳储量相对生长模型计算出碳储量作为参考值,用于评价基于估算的胸径和树高得到的杉木碳储量估计值的精度。评价指标包括R2、均方根误差(RMSE)、相对均方根误差(RMSEr)、相对误差(RE)和偏置(Bias)。
2 结果与分析
2.1 样地调查数据分析
样地1 和样地2 的小样方面积及杉木株数、胸径和冠幅情况见表1。由表1 可知,样地1 和样地2 的面积分别为774.2 m2和920.4 m2,两个样地的小样方面积分别在64.0 ~ 121.2 m2和77.3 ~ 122.9 m2之间。样地1 共有257 棵杉木,其平均胸径和冠幅分别为13.12 cm 和2.16 m,小样方中的杉木株数在14 ~ 37 棵之间,冠幅在2.36~ 2.96 m 之间,胸径在11.97 ~ 15.36 cm 之间。样地2 共有121 棵杉木,其平均胸径和冠幅分别为15.98 cm 和2.77 m,小样方中的杉木株数在9 ~ 21 棵之间,胸径在15.01 ~ 17.94 cm 之间,冠幅在2.23 ~ 3.11 m 之间。样地1 中的株数要大于样地2,样地2 中杉木的胸径和冠幅大于样地1 的。

表1 样地内杉木每木检尺调查数据Tab. 1 Tally of the sample plots
2.2 胸径与树高和冠幅建模
2.2.1 胸径与树高建模 利用2016 年森林资源二类调查小班杉木的平均胸径与平均树高,建立以胸径为自变量,树高为因变量的回归模型,两者散点图和表达式见图2。由图可知,样地1 和样地2 中杉木胸径和树高回归关系符合线性函数,其拟合决定系数R²分别为0.91 和0.89。对样地1 和样地2 中杉木胸径和树高关系式进行交叉验证得出,样地1 中杉木树高实测值与估计值之间的RMSE=0.79 m、RMSEr=11.29%、Bias=0.28 m;样地2 中杉木树高实测值与估计值之间RMSE=0.82 m、RMSEr=11.80%、Bias=-0.30 m。样地1 和样地2 中杉木胸径和树高回归模型精度分别为88.71%和88.20%,均能准确地预估杉木树高。

图2 胸径与树高模型构建与评价Fig. 2 Model establishment and evaluation between DBH and height
2.2.2 冠幅与胸径建模 利用实测的杉木冠幅和胸径数据,建立冠幅与胸径之间的回归模型,其散点图和表达式见图3A。由图可知,样地1 和样地2 中杉木的冠幅与胸径之间都存在较好的线性关系,拟合决定系数R2分别为0.55 和0.61。对样地1 和样地2 中杉木胸径和树高关系式进行交叉验证得出,样地1 中杉木实测胸径和估计胸径之间的RMSE=3.29 cm,RMSEr=25.41%;样地2 中杉木实测胸径和估计胸径之间的RMSE=3.31 cm,RMSEr=20.90%。样地1 和样地2 中杉木采用实测冠幅估算胸径的精度分别为74.59%和79.10%。
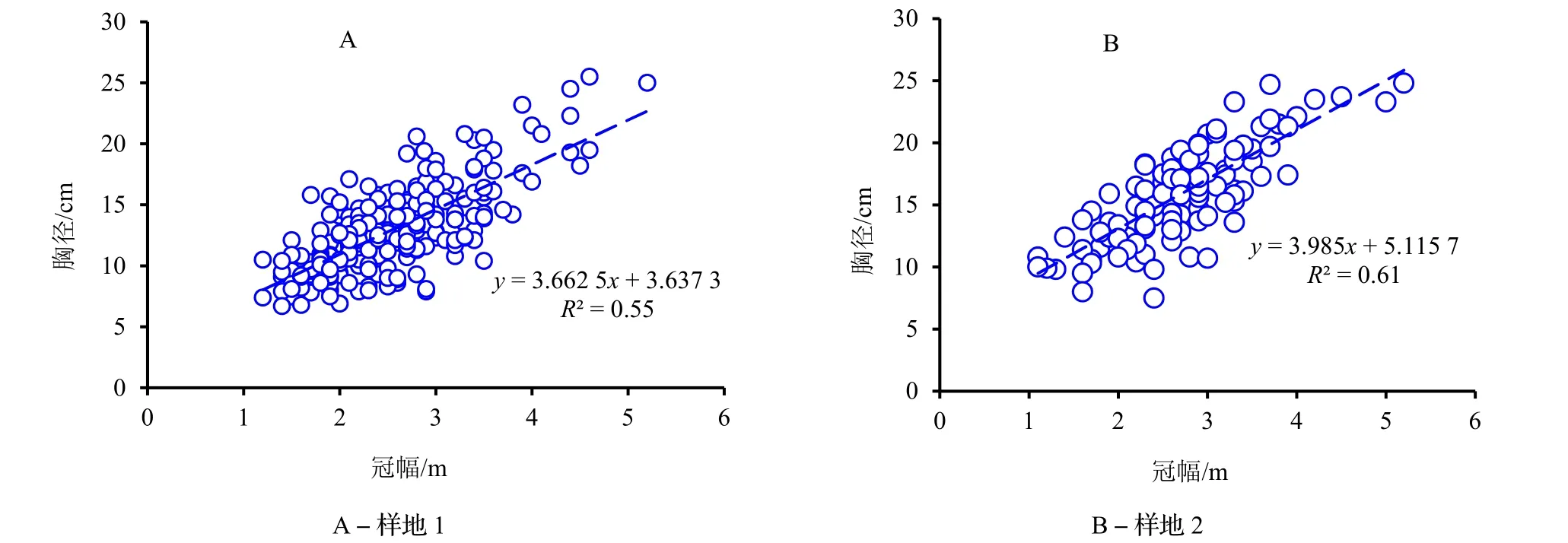
图3 冠幅与胸径模型构建与评价Fig. 3 Model establishment and evaluation between crown width and DBH
2.3 冠幅提取精度分析
以无人机影像绿光波段亮度值为特征值,采用放射线法提取样地1 和样地2 中杉木的冠幅。参考样地实测杉木冠幅最大值,样地1 和样地2 的窗口大小N分别为4.2 m 和4.9 m。树冠边缘点位置调整系数(α)和异常值剔除百分数(β)分别为0.1 和10%。分别以提取冠幅和实测冠幅为圆直径绘制杉木树冠边界,两个样地中杉木的冠幅提取结果见图4。从图4 可见,放射线法提取的杉木树冠边界与实测树冠边界能够较好地重合,但存在少部分树冠边界被明显放大和缩小问题。

图4 提取冠幅与实测冠幅对比图Fig. 4 Comparison on detected crown width and measured one
杉木的提取冠幅与实测冠幅之间存在显著(P<0.01)相关性,决定系数R2=0.22(图5A)。但大多数样本点聚集在1∶1 线附近,说明大部分树冠的冠幅能够被准确地提取,但是也存在较小的冠幅被高估和较大的冠幅被低估的情况。样地1 中杉木提取冠幅与实测冠幅之间的RMSE、RMSEr和Bias分别为0.63 m、24.10%和0.09 m;样地2 中杉木提取冠幅与实测冠幅之间的RMSE、RMSEr和Bias分别为0.79 m、28.45%和-0.22 m。从Bias可得出,样地1 中杉木的提取冠幅与实测冠幅之间系统误差很小,说明杉木的提取冠幅均值能够准确反映实测冠幅均值,但样地2 中杉木的提取冠幅存在系统高估。
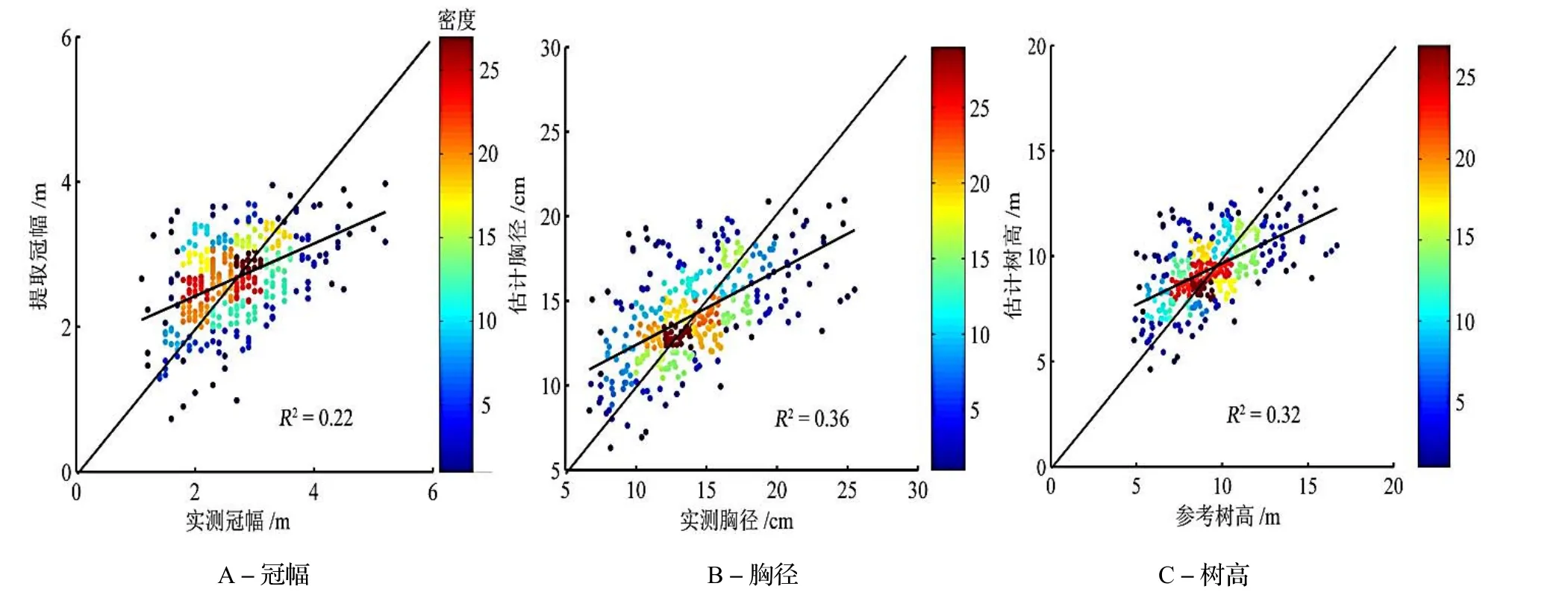
图5 杉木测树因子实测值与估计值之间散点图Fig. 5 Scatter plot of measured and estimated growth factors
将无人机影像提取的杉木冠幅代入杉木冠幅与胸径关系模型估算出胸径。由估计胸径与实测胸径对比结果表明(图5B),估计胸径和实测胸径之间R2= 0.36(P<0.01),大多数样本靠近1∶1 线,表明能够得到准确估算。样地1 中杉木估计胸径与实测胸径之间RMSE=2.85 cm、RMSEr=21.76%、Bias=0.27 cm,胸径估计值系统偏小;样地2 中杉木估计胸径与实测胸径的RMSE=3.47 cm、RMSEr=21.69%、Bias=-1.05,胸径估计值系统偏大。将杉木估计胸径代入胸径和树高关系模型进行树高估算,杉木估计树高与参考树高对比结果表明(图5A),估计树高和参考树高之间的R2=0.32(P<0.01),大多数样本能够得到准确估算。样地1 中杉木估计树高与参考树高的RMSE=1.79 m、RMSEr=20.16%、Bias=0.17 m,树高估计值系统偏小;样地2 中杉木估计树高与参考树高的RMSE=2.06 m、RMSEr=20.20%、Bias=-0.63 m,树高估计值系统偏大。
2.4 单株碳储量估算精度分析
将基于无人机影像提取的冠幅估计的胸径和树高代入杉木碳储量相对生长模型估计单株碳储量,并与参考的单株碳储量进行比较,结果如图6 所示。由图可知,样地1单株杉木碳储量估计值和参考值分别在3.92 ~ 35.49 kg 之间和4.46 ~ 86.53 kg 之间,两者平均值分别为19.27 kg 和21.46 kg。样地2 单株杉木碳储量估计值和参考值分别在15.07 ~ 53.72 kg 之间和5.55 ~ 78.36 kg 之间,两者平均值分别为34.40 kg 和31.50 kg。杉木的估计单株碳储量与参考单株碳储量的线性拟合R2为0.31(P<0.01),单株杉木碳储量较大的值存在明显的低估,但大部分样本靠近1∶1线,说明大部分样本能够被准确估计。杉木的估计单株碳储量与参考单株碳储量精度分析表明,样地1 中杉木单株碳储量估计值与单株碳储量参考值之间的RMSE=11.59 kg、RMSEr=54.00%、Bias=2.20 kg;样地2 中的RMSE=14.30 kg、RMSEr=45.40%、Bias=-2.90 kg,估计值系统偏大。样地1 和样地2 中的杉木单株碳储量估计精度分别为46.00%和54.60%,精度相对较低。

图6 单株碳储量估计值与参考值散点图Fig. 6 Scatter plot of estimated and reference carbon storage of individual tree
2.5 样地水平测树因子和碳储量估算精度分析
将两个样地内单株杉木碳储量累加得到样地1 碳储量估计值和参考值分别为63.98 t·hm2和71.27 t·hm2,样地2 碳储量估计值和参考值分别为45.23 t·hm2和41.42 t·hm2。由样地尺度杉木测树因子和碳储量估计值与参考值的精度比较得出(表2),样地1 的9 个小样方中杉木的平均冠幅、胸径、树高和碳储量估计值的RE变化幅度分别在-8.64% ~ 13.64%、-9.19% ~ 15.22%、-8.45% ~ 14.25%和-16.80% ~ 33.35%之间。样地2 的 9 个小样方中杉木的平均冠幅、胸径、树高和碳储量估计值的RE变化幅度分别在-34.90% ~ 5.50%、-35.11% ~ 5.58%、-32.13% ~ 5.23%和-80.52% ~ 13.16%之间。整个样地的平均冠幅、胸径、树高和碳储量估计值的RE都低于11%。样地2 的第9 个小样方中的杉木冠幅估计值明显高估,导致其他因子估计精度也较低。相对单株尺度精度而言,在小样方和整个样地水平上的各测树因子和碳储量估计值精度都得到明显提高。样地1 和样地2 水平各测树因子及碳储量精度分别在89.77%和90.79%以上。
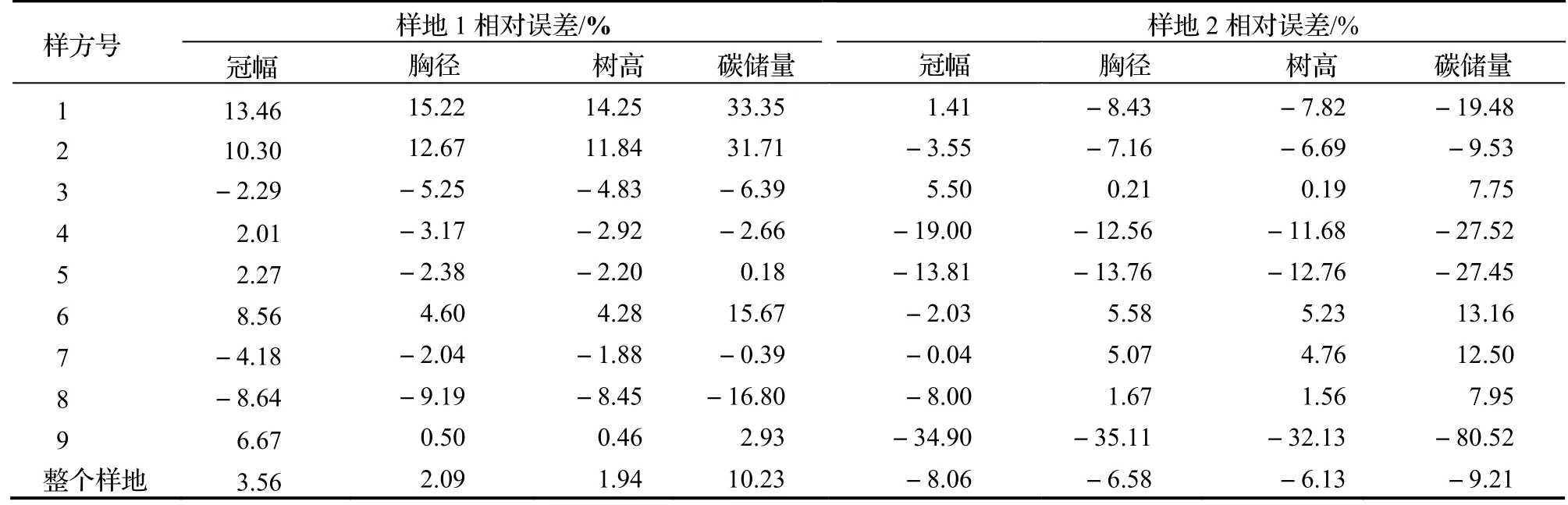
表2 样地水平测树因子和碳储量估计值相对误差Tab. 2 Relative errors of the growth factors and carbon storage estimation at the sample level
3 结论与讨论
3.1 讨论
(1)结合无人机可见光影像和放射线法提取的杉木林中的杉木冠幅与实测冠幅之间存在较高的误差,主要原因是实测冠幅采用自下而上观测方式,受冠层重叠遮挡影响小,而基于无人机影像自上而下观测树冠,受冠层重叠遮挡影响较大,往往造成提取冠幅小于实测值[17]。另外,受树冠内孔隙阴影等影响,使得树冠内阴影像元被误判为树冠边缘点,造成提取冠幅小于实测值[25]。受林下植被等影响,树冠边缘像元与背景像元非常接近,将背景像元误判为树冠边缘点,使得提取冠幅高于实测值。
(2)单木碳储量估计精度较低的主要原因是基于无人机提取的单木冠幅、胸径和树高精度还不够准确,存在高值低估和低值高估的问题。此外,仅采用冠幅一个变量估算胸径也存在不足,研究表明以冠幅和树冠面积为自变量能够提高胸径估算精度[17]。胸径和树高之间的关系受立地条件、林分条件和竞争等影响,不同区域或样地之间具有差异性[26]。构建含林分变量或基于混合效应的树高和胸径关系式,能提高树高预测精度[26]。对于整个样地,高估和低估的冠幅估计值相互抵消后,样地的平均冠幅、胸径和树高估计值精度明显提高,进而样地碳储量精度也较高。本研究树冠中心点采用目视解译方法获取,未考虑株数提取误差对样地碳储量估计精度影响。
3.2 结论
本研究利用无人机可见光影像,采用放射线法实现了杉木单木冠幅自动提取,然后基于无人机影像提取的冠幅数据,结合样地调查数据建立的冠幅-胸径以及胸径-树高回归模型,估计出单木胸径和树高,将两者代入杉木碳储量相对生长模型估计单株和样地碳储量。由上述方法得到的单木冠幅、胸径、树高和碳储量精度相对偏低,存在高估和低估问题,说明本研究方法在估算单木尺度杉木结构参数和碳储量上精度还有待提高。但将尺度上升到与浙江省森林资源连续清查标准样地面积时,样地平均冠幅、胸径、树高和碳储量估计精度在89%以上。本研究方法能够满足样地尺度的冠幅、胸径、树高和碳储量估算精度要求,具有较高的实用性。

