堰槽组合量水设施水力性能数值模拟研究
凌 刚,王文娥,王 惠,胡笑涛
▪灌溉水源与输配水系统▪
堰槽组合量水设施水力性能数值模拟研究
凌 刚,王文娥*,王 惠,胡笑涛
(西北农林科技大学 旱区农业水土工程教育部重点实验室,陕西 杨凌 712100)
【目的】堰槽组合量水设施适用于流量变幅较大的山区溪流流量测量,以数值模拟的手段全面分析其流场分布规律和水力特性,以期为堰槽组合量水设施的结构优化提供理论依据。【方法】在模型试验的基础上,采用FLOW-3D软件对10.13~200.00 L/s(试验最大流量的2.8倍)范围内的17种流量工况下该设施的水力性能进行数值模拟,分析了槽内流和堰槽流的沿程水深、佛汝德数()及流速的变化规律。【结果】所有流量工况下堰槽组合量水设施中心纵剖面和流速均沿程先增大后减小,呈单峰分布;设施上游水流平稳,为0.1~0.3,流速为0.08~0.5 m/s,随流量的增加逐渐加大;水流进入该设施后,和流速急剧增大;设施下游出现较大范围的薄水层区域,最大值达到3.0~4.6,流速最大值为1.05~2.06 m/s;槽内流时下游产生弱水跃,堰槽流时下游均为急流(>1),同时扩散水流在侧岸处发生折冲,产生菱形波;流量小于100 L/s时,模型试验建立的测流公式最大相对误差为6.11%,流量超过100 L/s时,相对误差逐渐增大。对流量大于100 L/s的模拟结果进行分析,建立了流量大于100 L/s时的测流公式,该公式相对误差小于0.87%,满足河流量水要求。【结论】基于FLOW-3D软件对堰槽组合量水设施进行的水力性能数值模拟与模型试验有着较好的一致性,建立了大流量下的测流公式,扩充了堰槽组合量水设施的测量范围。
堰槽组合;数值模拟;佛汝德数;水力特性;FLOW-3D
0 引言
【研究意义】河流水位、流量监测是水资源利用的重要基础数据,我国主要河流均已建立水文测站。但山区溪流数量多、位置偏远,汇流时间短且变幅大,更易受降水和汇流条件等因素的影响,适宜的流量监测设施匮乏[1-5]。【研究进展】目前山区河流量水设施的研究主要为量水堰,如Piton等[6]通过长期的小尺度水槽试验研究了拦河堰对山区陡坡河流上高度波动的推移质输沙的影响,结果表明拦河堰能改善河流侵蚀及泥沙传播的规律;Kupferschmidt等[7]通过室内堆石堰水力性能模拟试验,分析堰的几何形状、河床坡度对堆石堰中的水流流态、速度、湍流动能等湍流特性的影响,并提出V形堆石堰有利于鱼类迁徙。但横跨整个河道的拦河堰容易造成上游水位壅高、泥沙淤积等问题,流量较小时堰上水头过小,测流精度低;流量较大时容易引起下游冲刷,失去流量监测功能。灌区特设量水设施已超过100多种,主要为量水槽和量水堰等,诸多学者[8-13]研发的机翼型量水槽、梯形喉口无喉道量水槽、梯形薄壁侧堰、三角形长喉道量水槽及量水柱等,这些量水设施主要适用于断面规则、流量变幅不大的灌溉渠道。针对山区季节性溪流流量变化大导致量水精度低的问题,Wessels等[14-15]、王文娥等[16]提出堰槽组合量水设施,通过试验建立了测流公式,分析了薄水层区域、垂线纵向时均流速等水力特性。
当前,计算流体动力学(CFD)方法凭借成本低,可视化程度高的优势被广泛应用在各种复杂结构的流场模拟分析,成为研究结构参数与水流内部流场关系的有效手段[17-22]。数值模拟软件Fluent、FLOW-3D等不仅常应用在水轮机[23-25]、涡轮机[26]、泄洪洞[27]等大型水工建筑物的水力特性研究中,对渠道侧堰[28]、田间便携式短喉槽[29]、梯形喉口无喉道量水槽[30]、明渠[31]等小型水工建筑物的水力性能模拟研究也十分常见,其研究结果也均表明数值模拟结果能够与试验结果整体吻合较好,模拟方法可行、湍流模型适用,并可通过对不同结构设施的水力性能数值模拟结果进行结构优化。
【切入点】由于堰槽组合量水设施结构复杂,不同流量范围内过流宽度及水深差异较大,需全面分析不同流量范围内的流场分布规律及影响因素,为结构优化提供依据,而通过模型试验[16]分析得到的水力特性存在一定的局限性,对于流速等水力特性在空间上的分布规律还有待深入研究。【拟解决的关键问题】因此,本研究在模型试验的基础上,采用FLOW-3D软件对该量水设施在10.13~200.00 L/s(试验最大流量的2.8倍)范围内的水力性能进行数值模拟研究,分析不同流量条件下堰槽组合量水设施水深、佛汝德数等沿程变化,流速分布规律及影响因素,进一步改进和扩充流量公式。
1 数值模型建立
1.1 堰槽组合量水设施结构
堰槽组合量水设施[16]如图1所示,其结构包括排淤量水槽以及两侧的克伦普堰,其中排淤量水槽沿水流方向依次为分水段、矩形段、过渡扭面段和梯形窄段4个部分;两侧克伦普堰迎水面坡度为1∶2,背水面坡度为1∶5。堰槽组合量水设施利用堰、槽具有的稳定水位与流量关系,小流量时槽内过流(槽内流)、大流量时槽与堰同时过流(堰槽流),可在较大的流量范围内均达到较高的量水精度,对山区溪流流量变幅大的特点具有很大的监测优势;中部的量水槽还具备排沙冲淤及为鱼类提供生态通道的作用;两侧堰体可控制主流方向,防止水流冲刷两侧岸坡,同时增加上游水深,满足鱼类和浮游生物生存需求。
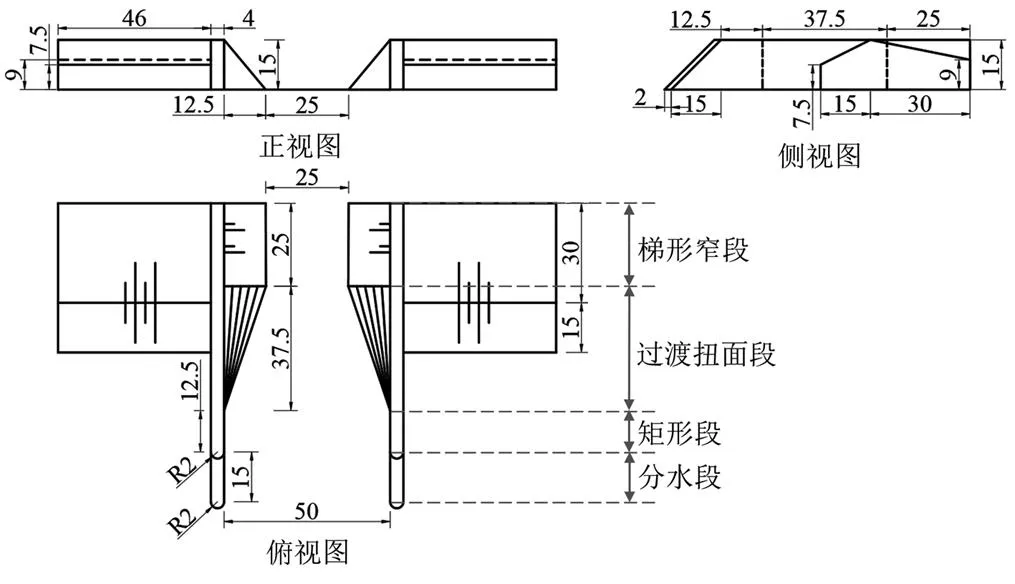
图1 堰槽组合量水设施三视图(单位:cm)
堰槽组合量水设施测流机制试验研究中,以距离量水设施进口前120 cm处的断面为起始断面沿中轴线布置测点,上游段6个测点(M1~M6),排淤量水槽12个测点(1~12),槽外出口段5个测点(13~17),下游薄水层区域5个测点(S1—S5),共28个测点。测点位置如图2所示,测点1~17所在断面到起始测点所在断面的距离详见表1。
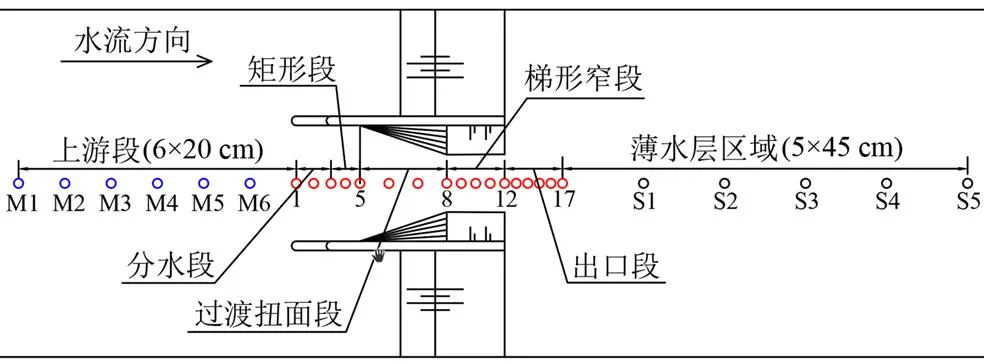
图2 堰槽组合量水设施测点布置

表1 量水槽槽内及出口段控制断面位置
1.2 数值模拟控制方程
堰槽组合量水设施的过流为不可压缩流体运动,可由下面的连续性方程和雷诺方程[32-33]描述。

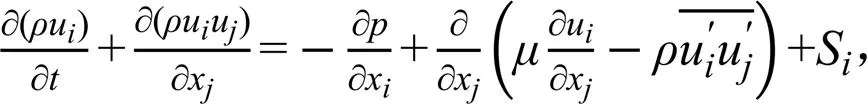
由于水流从进入堰槽组合量水设施时,断面大小急剧变化,流线弯曲,适宜采用RNG模型[12]。故本文选用RNG紊流模型。湍动能和湍动能耗散率方程[33]分别为式(3)和式(4)。
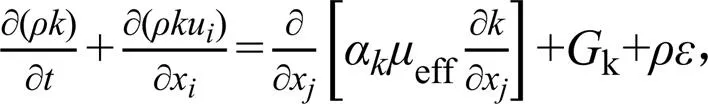
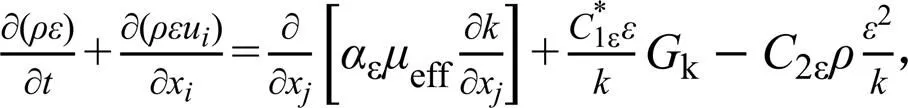
1.3 模型范围及网格划分
本文根据堰槽组合量水设施模型试验尺寸建立三维几何实体模型,为保证水流流态不受进出口条件的影响,综合考虑模拟运行时间,选取堰槽组合进口上游4 m(大于25倍堰高及30倍最大堰上水头)和出口下游5.83 m(实际下游至尾水的长度)的区域进行模拟。
通过4种宽度(3.0、2.5、2.0 cm和1.0 cm)的均匀网格、流量为78.7 L/s时的模拟结果,对上述模型范围的整个计算域进行了网格无关性检验,图3给出了4种网格尺寸下模拟得到的沿程水深。由图3可知,当网格宽度为2 cm和1 cm时,模拟结果已经接近稳定,沿程水深已基本不再变化,综合考虑模拟运行时间和精确度,本研究拟对全计算区域选用网格尺寸为2 cm´2 cm´2 cm进行网格划分,又由于在模型试验中,小流量情况下(=10.02 L/s和19.98 L/s等)堰后薄水层区域水深较浅,为适当提高精度,防止累计误差带来的影响,所以在对全体计算域采用2 cm´2 cm´2 cm网格进行划分的基础上,再次对堰后3 m的区域(即图3中=210~510 cm)用尺寸为1 cm´1 cm´1 cm的网格进行加密处理,整体计算域网格数量约为322万。

图3 不同网格大小稳定后沿程水深
1.4 计算方法与边界条件
对流项采用二阶迎风格式,扩散项采取二阶中心差分格式,最小时间步长为10-7s。对自由表面的模拟计算采用FLOW-3D独特的Tru VOF方法,其只计算含有液体单元不考虑气体单元的计算方式能够更为准确的追踪自由液面的变化[28]。
渠道上游进口边界设为流量进口边界,并根据试验中实测流量设置流量值,从10.13~70.63 L/s共8种流量工况(10.13、19.92、30.08、32.75、40.15、50.30、60.04、70.63 L/s),其中32.75 L/s为槽内流与堰槽流的流量阈值;为进一步研究量水设施在大流量情况下的相关水力特性,选取80~200 L/s范围内,共9种流量工况(80、90、100、110、120、140、160、180、200 L/s),共计17种模拟流量;下游出口设置为自由出流边界;渠道底部及侧壁均选择无滑移固壁边界;渠道顶部空气入口设为压力值与水体体积分数值均为0的压力边界,边界条件设置如图4所示。
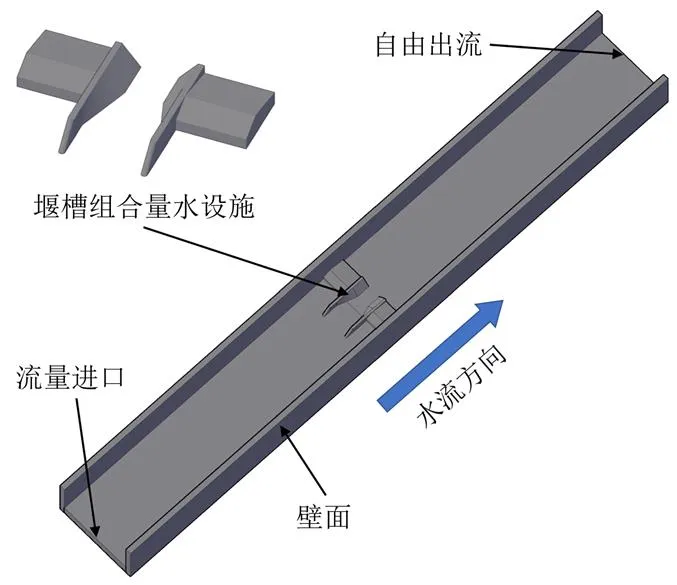
图4 三维模型与边界条件
2 数值模拟可靠性验证
为验证模拟结果的准确性,根据模型试验得知槽内流与堰槽流的流量阈值为32.75 L/s[16],因此选取了流量阈值范围内外4种流量(19.92、32.75、40.15、60.04 L/s)下渠道中心纵剖面沿程水面线的试验及数值模拟结果进行对比(图5)。从图5可以看出,4种流量下水面线沿程变化的模拟结果与试验吻合。
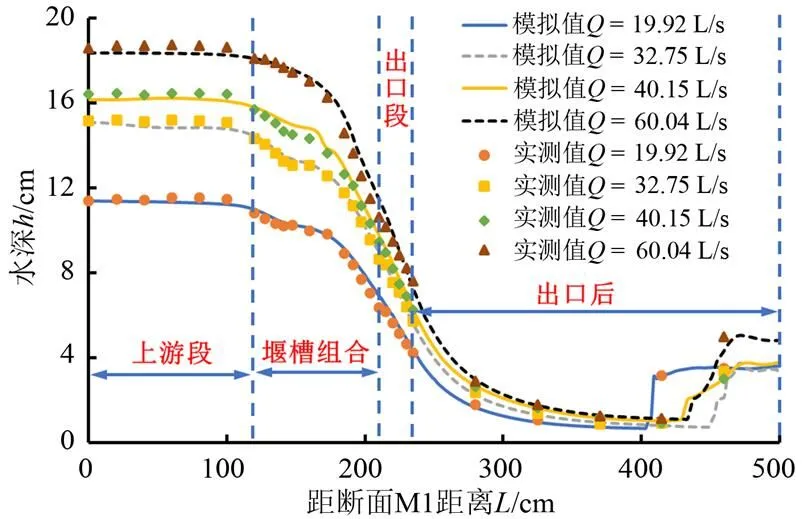
图5 不同流量下渠道中心纵剖面水面线变化规律
结合图5与图6,当流量小于阈值时,槽内过流,在排淤量水槽进口上游水面线平稳,水流相对平顺;水流刚进入排淤量水槽时,经迎水面为45°倾角的半圆柱状隔墙的分水段得以平稳过渡,进而流入排淤量水槽内,水面开始下降;进入矩形段后水面线下降幅度进一步减小,呈相对平缓的状态;进入过渡扭面段后,槽内两侧水流开始发生交叉,在槽中线汇聚,水面在承接前一段相对平缓的状态后跌落较为明显;最后进入梯形窄段,该段水面线下降最快,出现临界流,水流由缓流变至急流;当水流流出排淤量水槽来到出口段时,因过流断面突扩,水面线进一步下降,水流流态呈放射状,并在下游出现两侧水深大,中间水深小的薄水层区域;同时,两侧的堰后出现回流区。当流量大于阈值时,槽内过流和堰顶溢流同时发生,堰后出现水流冲击区域,且在设施下游,因渠道两侧对放射状水流的约束作用,过流水流产生了扩散、汇集、再扩散的过程,呈菱形波的形态逐渐向下游发展。
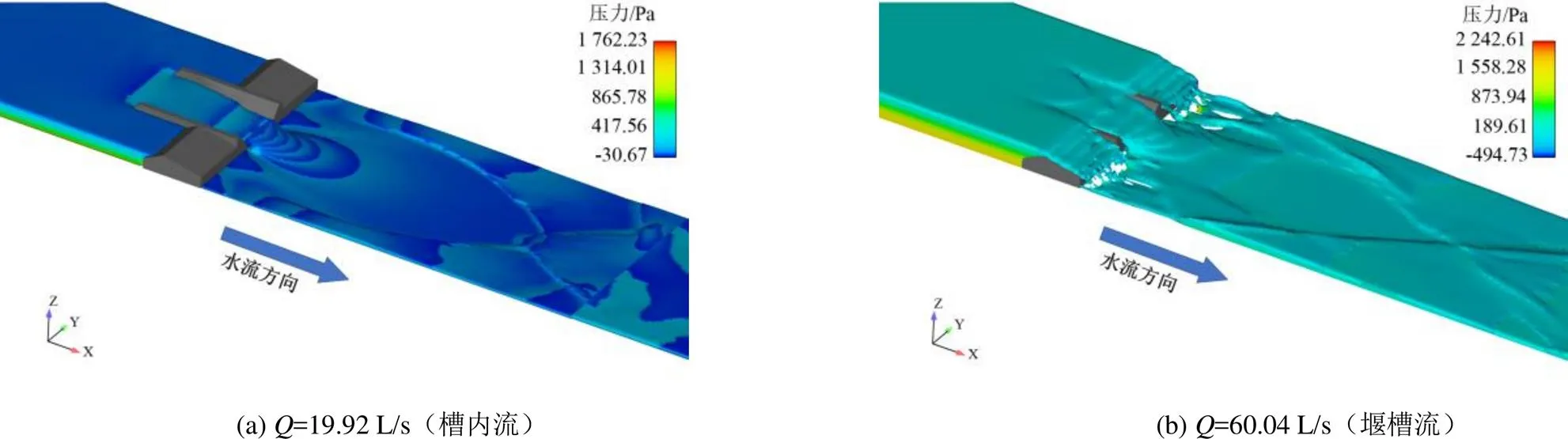
图6 堰槽组合量水设施模拟流态
在模型试验中,测点4的水深(4)与综合流量系数的相关性最强,其水深是进行流量计算的基础[16],所以将模拟工况测点4的模拟水深与实测结果对比分析,如表2所示,所有工况最大相对误差均在5%以内,表明本研究采用的数值模拟方法合理可靠。

表2 不同流量下测点4模拟水深值与实测水深值对比
3 结果与分析
3.1 佛汝德数分析
佛汝德数()是明渠流重要的无量纲数,可作为判别水流流态的标准。根据模拟结果,选取设施上下游分布的3种典型情况(=19.92、60.04、160.00 L/s,图7)。第一种是水流只通过的排淤量水槽过流(槽内流)的情况,如图7(a)所示,在上游较小且稳定均匀,经过量水槽之后逐渐变大,在槽后薄水层区域呈放射状分布,随后逐渐变小向下游发展;第二种如图7(b)所示,槽内流与堰顶溢流同时发生(堰槽流),在堰后冲刷区极大,槽后放射状分布经两侧渠道的约束更显集中,呈三角分布,在尖角处值更大,下游整体与流态分布一致,呈菱形波的形态;第三种如图7(c)所示,其堰后冲刷区值相比于图7(b)更小,槽后的三角区域更小,下游也呈现菱形波的分布,虽然该情况下过流水流也是槽内流与堰顶溢流同时发生,但分布情况更接近堰流,通过槽内的水流对整体分布的影响逐渐降低。
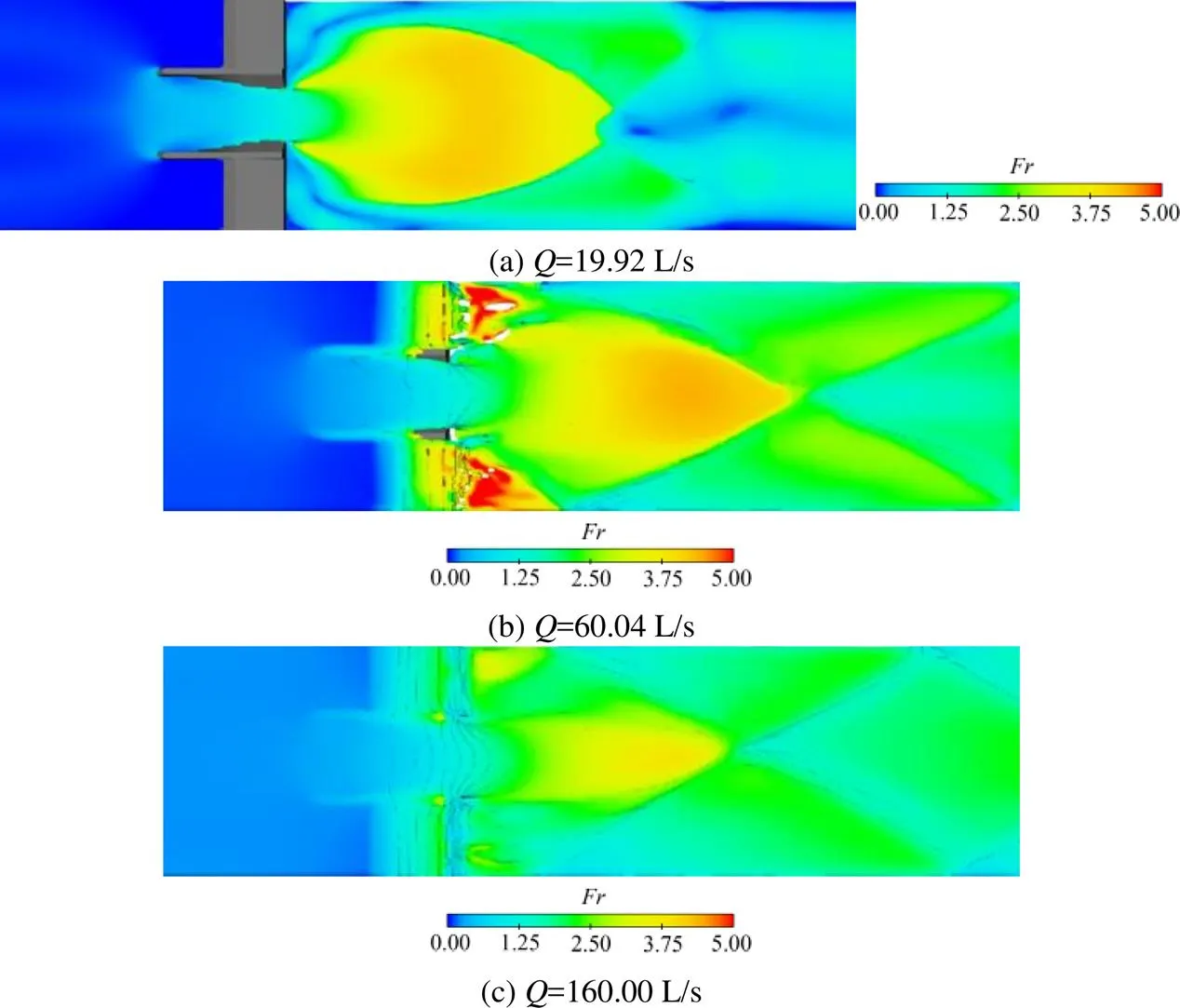
图7 不同流量下Fr分布
图8给出了不同流量工况下渠道中心纵剖面沿程变化规律。在流量小于流量阈值32.75 L/s(图8(a))时,沿程变化总体趋势相似,呈现单峰分布,在上游段值基本稳定在0.1左右,波动幅度很小,当水流进入到排淤量水槽之后,过流断面面积的逐渐减小导致值逐渐增大;水流流出排淤量水槽之后,进入薄水层区域,进一步增大至峰值后逐渐下降,同时有突变点产生,突变点处急剧减小,之后稍有起伏,但基本保持稳定。并且,随着流量的增大,最大值位置和突变点位置逐渐向下游发展。
当来水流量大于流量阈值32.75 L/s时,如图8(b)所示,总体变化规律呈单峰分布,随着流量的增大,最大值逐渐增大,最大值位置也逐渐向下游发展,但当流量达到80 L/s之后,最大值却逐渐减小,最大值位置逐渐向上游发展;同样产生了急剧减小的突变点,但所有模拟工况的并没有急剧减小到1以下,表明出口后的水流均是急流流态,突变幅度随着流量的增大逐渐减小,突变位置随着流量的增大逐渐向上游移动。
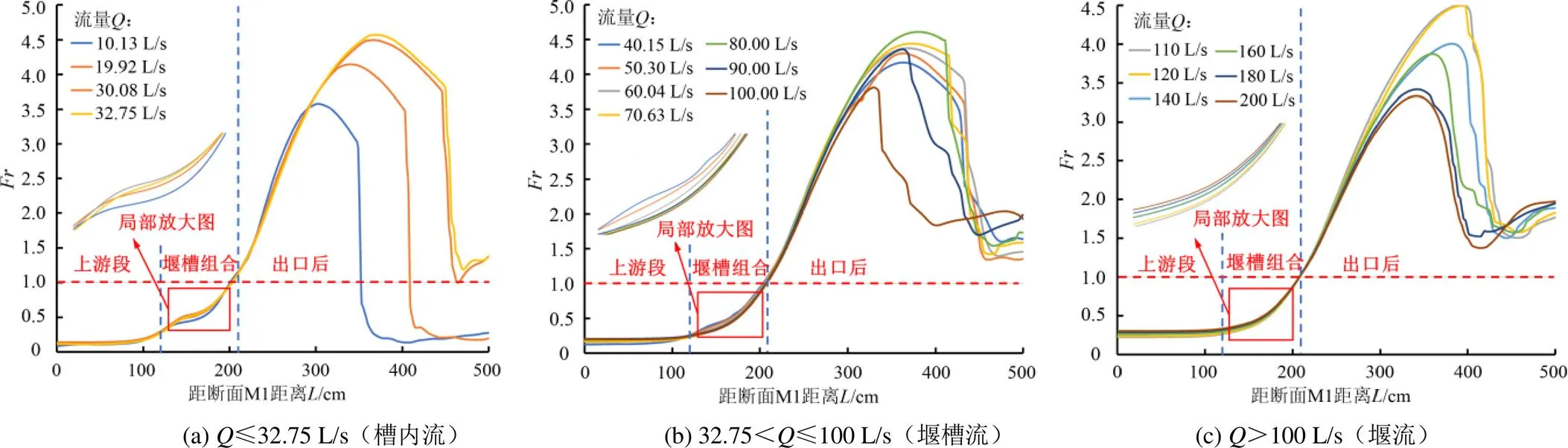
图8 不同流量下渠道中心纵剖面Fr沿程变化规律
值得注意的是,结合图8(a)和图8(b),在来水流量小于30.08 L/s时,突变点处的急剧减小到了1以下,说明该处的水流形成了临界流,水流由急流变为缓流,而来水流量大于等于30.08 L/s之后,突变点处的虽然同样急剧减小,但并没有小于1,表明在大流量情况下,薄水层区域的结束并不是由于水跃现象的产生,而是由于两侧渠道对堰槽后放射状冲击水流的约束,水流经侧岸阻挡,折冲至薄水层区域,薄水层提前结束。
然而,当流量达到110 L/s时,如图8(c)所示,最大值并没有按照80~100 L/s的规律逐渐减小,而是突然变大,最大值位置也突然下移;之后,随着流量的增大又恢复了最大值逐渐减小,最大值位置逐渐向上游发展这一变化规律;并且在=1处明显产生交点,即各工况的临界水深断面的位置都在梯形窄段和出口段的交界处(=210 cm)。
从图8中堰槽组合段内(=120~210 cm)的变化规律的局部放大图可以看出,槽内流时,堰槽组合段内的变化曲率有一个放缓的过程(即曲线的斜率有一段减小的过程);随着流量的增大,在堰槽流时,这个过程逐渐消失,该段曲线逐渐变得平滑;图8(c)的局部放大图中,曲线的变化曲率已经没有放缓的过程(即曲线斜率一直增大),这说明随着流量的增大,排淤量水槽对水流的影响逐渐减弱直到几乎无影响。并且,图8(b)的局部放大图中,堰槽组合段内的值随流量的增大逐渐减小,图8(c)的局部放大图中,堰槽组合段内的值随流量的增大逐渐增大,2种变化规律的不同说明这是2种形式的水流流态,即堰槽流和堰流。这说明本研究在原模型试验以32.75 L/s区分槽内流与堰槽流的基础上,以100 L/s再次将堰槽流与堰流进行区分是有一定意义的。
3.2 流速分析
流速分布决定了设施上游泥沙淤积和下游冲刷程度。图9为不同流量工况下渠道中心纵剖面速度沿程变化规律。从图9可知,在流量小于流量阈值32.75 L/s时,渠道中心纵剖面沿程变化总体趋势相似,同佛汝德数变化规律一样呈单峰分布,峰值随流量的增大而增大;在上游段(=0~120 cm),流速变化从基本稳定逐渐缓慢增大,变化曲率较小,增幅不大,进入排淤量水槽之后,过流断面收缩,流速变大,变化曲率增大,在过渡扭面段(=147.5~185 cm)曲率有轻微减小,进入梯形窄段(=185~210 cm)之后,流速大幅增长,流出排淤量水槽后达到峰值,后缓慢下降,薄水层结束位置处流速急剧下降,同佛汝德数的变化规律相对应。当来水流量大于流量阈值32.75 L/s小于100 L/s(堰槽流)时,整体变化规律呈单峰分布,且随流量增大,流速峰值逐渐增大,各流量工况下的流速曲线在过渡扭面段和梯形窄段之间还有交点产生,上游段流速变化同流量阈值内的变化一致,进入排淤量水槽之后,流速急剧增大,变化曲率增大,达到峰值后缓慢下降,在薄水层之后流速开始变得相对稳定。在流量超过100 L/s(堰流)之后,出口后的流速有一段急剧下降的过程,且下降点逐渐向上游发展,与堰槽流有所不同的是,堰流的流速曲线在过渡扭面段和梯形窄段之间无交点产生,流速随流量的增大而增大。
为进一步探究水流运动的基本规律,以流速流线分布图来描述水流的运动状态能够更为直观,图10和图11分别是=19.92和70.63 L/s时模拟的流速流线沿程分布图。从图10可以看出,在流量阈值内,槽内流时,从上游段开始,流速逐渐增大,流线因为过渡扭面段和梯形窄段的收缩而逐渐变得密集,水流流出排淤量水槽之后,流线呈放射状向外延展,经渠道边壁的约束作用后向渠道中心汇集,且两侧堰的堰后产生了回旋区。水流经过扩散、碰撞和再汇集之后流速相对减小。从图11可知,在流量阈值外,上游段和量水槽内,流速分布和在阈值内时同样有一个向中心集中的过程,流出量水槽之后也呈放射状分布;不同的是,两侧堰堰顶有水流过流,堰前有部分水流跨过侧壁向量水槽内汇集,堰后回旋区由冲刷区代替,由于流速更大,渠道边壁的约束作用更明显,流过水槽的水流产生了扩散、汇集、再扩散的过程,过流水流呈现菱形波的形态逐渐向下游发展。

图9 不同流量下渠道中心纵剖面速度沿程变化规律
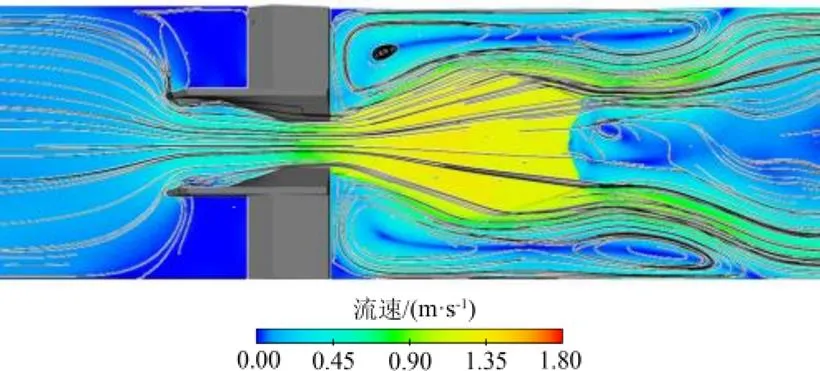
图10 Q=19.92 L/s时流速流线沿程分布
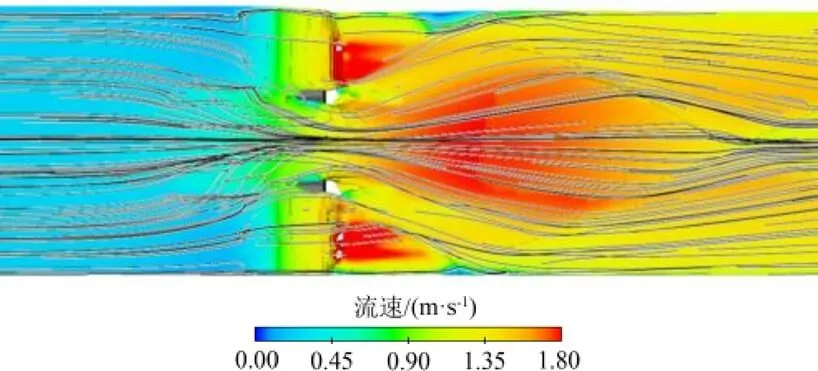
图11 Q=70.63 L/s时流速流线沿程分布
3.3 流量公式与测流精度
在模型试验研究中[16],通过临界断面水深与流量的关系,结合能量方程推导出了槽内流流量公式(式(5)—式(6)),此时测点4水深需满足4/≤0.885;将迷宫堰与克伦普堰的流量公式相结合,建立了堰槽流流量公式(式(7)—式(8)),此时测点4水深需满足4/≥0.885。
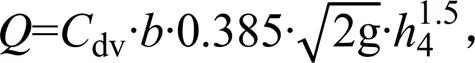



式中:为流量(m3/s);dv为堰槽组合量水设施槽内流时的综合流量系数;为排淤量水槽出口底部宽度(m);4为距断面M1距离=141.25 cm的测点4(槽内矩形段中间断面)的水深(m);为排淤量水槽高度(m);0为堰槽组合量水设施堰槽流时的综合流量系数;w为堰槽组合量水设施的有效过水宽度,为两侧堰的堰宽加上量水槽侧壁进口至与堰顶齐平处的长度总和(m);为侧堰的堰高(m)。
将所有模拟结果中测点4的水深带入上述流量公式,得到堰槽组合量水设施模拟值与计算值的误差如表3所示。由表3可知,在流量阈值内相对误差最大为4.78%;在流量阈值外相对误差呈现先减小后增大的规律,在80 L/s左右达到最小值-1.12%。由于堰槽组合量水设施适宜于流量较小的山区溪流流量测量,测流精度要求较高,由表3可知,当流量超过100 L/s之后,绝对误差已经达到-7.74 L/s,相对误差达到-7.04%,结合图8(b)和图8(c)中的变化趋势看,在80~100 L/s之间发生突变,无明显规律,流量达到110 L/s后又逐渐规律起来;综合考虑,文献[16]中堰槽组合量水设施模型试验得到的流量公式适用范围是0~100 L/s。
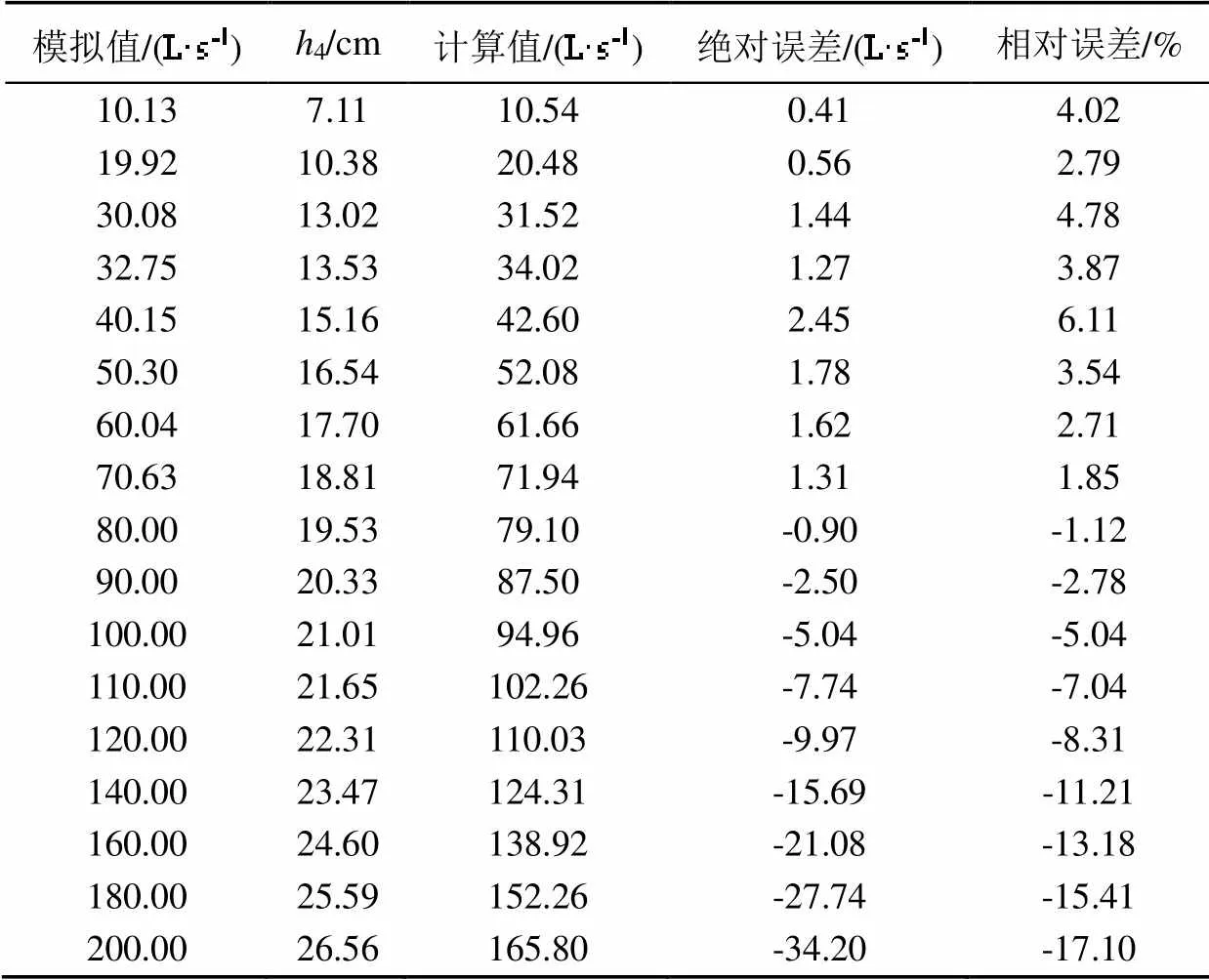
表3 模拟流量值与计算流量值对比
为完善堰槽组合量水设施的流量公式,扩大测量范围,将110~200 L/s的模拟结果进行进一步研究。同文献[16]的研究相同,采用迷宫堰和克伦普堰相结合的公式:
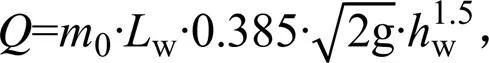
式中:w为堰槽组合量水设施上游测点水深减去堰顶高度后的水深,本研究中取w=M1-,M1为堰槽组合量水设施上游段M1处的水深(m)。
根据模拟结果对0进行公式拟合,得到式(10),其相关系数达0.992 5,图12为来水流量在110~200 L/s范围内,堰槽组合流量系数0随着测点M1的相对作用水头w/(w+)的变化情况。

但在试验中发现,上游段常常会有淤积现象而导致M1点水深产生测量误差,需要在不会产生淤积的量水槽内找一个测点水深代替测点M1水深,研究发现量水槽中测点4与测点M1有较强相关性,图13为测点4与测点M1在110~200 L/s流量范围内二者的水深关系图,其拟合的经验公式如式(11),复相关性达到0.999 9。

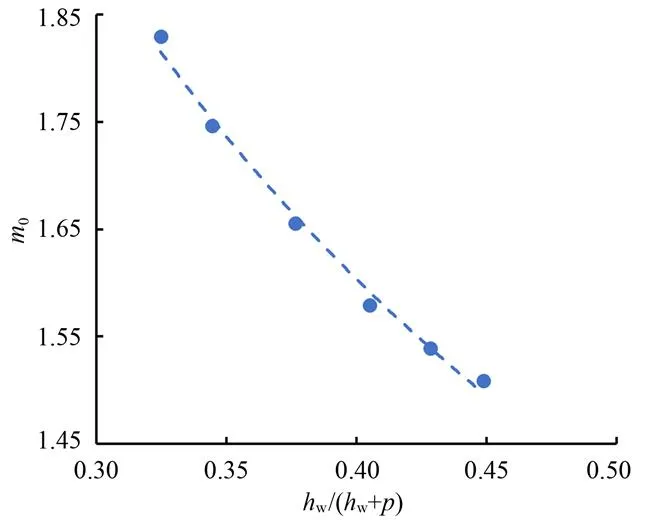
图12 堰槽组合流量系数随相对作用水头的变化

图13 测点4与测点M1之间的相对水深关系
综合前文,得到流量式(12)和式(13),此时测点4水深需满足4/d≥1.4。将流量大于100 L/s的6种流量工况下测点4的模拟水深代入公式(式(12)—式(13))得到计算流量值,与模拟值对比结果见表4。由表4可知,最大流量相对误差为-1.08%,相对误差绝对值的平均为0.54%,所有相对误差的绝对值均小于1%,满足河流量水要求,说明拟合的流量公式计算精度较高,能有效推广应用。
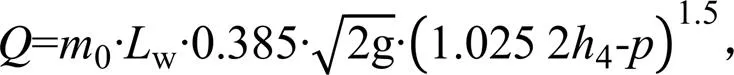
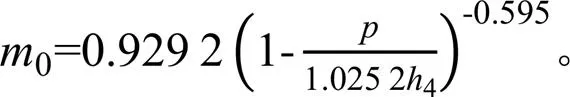

表4 模拟流量值与计算流量值对比结果
4 讨论
堰槽组合量水设施的研究相对较少,Wessels等[15]仅给出了槽内流和堰槽流的判别和流量计算公式,王文娥等[16]在此基础上分析了中垂线纵向时均流速、槽内中垂线佛汝德数的变化,但对于空间平面上的流速分布并未做深入探究。本研究中采用数值模拟这一可视化程度较高的手段对堰槽组合量水设施进行分析,得到中垂线佛汝德数和流速在量水槽内时的变化规律与王文娥等[16]的一致,并在此基础上增加了对量水槽上游和下游水力特性变化规律的分析,同时展示了过流水力特性在空间上的分布。此外,还弥补了模型试验中流量范围不够大的缺点,建立了大流量下新的测流公式,扩大了堰槽组合量水设施的测量范围。
本文仅对一种结构参数的堰槽组合量水设施进行了数值模拟研究,为该堰槽组合量水设施的改进和优化提供了相关理论依据。对于槽宽、堰顶坡度等结构参数对堰槽组合水力性能的影响还有待进一步研究。
5 结论
1)采用RNG紊流模型模拟堰槽组合量水设施过流水流流动,水深最大相对误差均在10%以内,水流流态变化规律相一致,通过数值模拟的方法进行量水设施水力性能的探究是可行的。
2)17种流量(范围10.13~200.00 L/s)下堰槽组合量水设施中心纵剖面和流速均沿程先增大后减小,呈单峰分布;设施上游水流平稳,为0.1~0.3,流速为0.08~0.5 m/s,随流量的增加逐渐加大;水流进入该设施后,和流速急剧增大;设施下游出现较大范围薄水层区域,最大值达到3~4.6,流速最大值为1.05~2.06 m/s;除槽内流时(小流量)下游产生弱水跃,堰槽流时(流量较大)下游均为急流(>1),同时扩散水流在侧岸处发生折冲,产生菱形波。
3)在来水流量小于100 L/s时,模型试验建立的测流公式最大相对误差为6.11%,超过100 L/s之后,相对误差将逐渐增大甚至超过10%;结合变化规律,得到模型试验建立的测流公式最适宜的测流范围是0~100 L/s(对应4/≤1.4)。建立了流量大于100 L/s时(对应4/>1.4)新的测流公式,新测流公式的最大相对误差为-0.87%。
(作者声明本文无实际或潜在利益冲突)
[1] 吴志勇, 徐梁, 唐运忆, 等. 水文站流量在线监测方法研究进展[J]. 水资源保护, 2020, 36(4): 1-7.
WU Zhiyong, XU Liang, TANG Yunyi, et al. Research progress of on-line discharge monitoring methods in hydrometry stations[J]. Water Resources Protection, 2020, 36(4): 1-7.
[2] 徐立中, 张振, 严锡君, 等. 非接触式明渠水流监测技术的发展现状[J].水利信息化, 2013(3): 37-44, 50.
XU Lizhong, ZHANG Zhen, YAN Xijun, et al. Advances of non-contact instruments and techniques for open-channel flow measurements[J]. Water Resources Informatization, 2013(3): 37-44, 50.
[3] 张振, 徐枫, 王鑫, 等. 河流水面成像测速研究进展[J]. 仪器仪表学报, 2015, 36(7): 1 441-1 450.
ZHANG Zhen, XU Feng, WANG Xin, et al. Research progress on river surface imaging velocimetry[J]. Chinese Journal of Scientific Instrument, 2015, 36(7): 1 441-1 450.
[4] 周昱瑛, 刘信华, 黄伟军. 山区河流主要特性分析及滩险整治方法初探[J]. 水运工程, 2005(1): 50-54.
ZHOU Yuying, LIU Xinhua, HUANG Weijun. Characteristics analysis of mountainous rivers and regulation method investigation of rapids[J]. Port & Waterway Engineering, 2005(1): 50-54.
[5] 曹浩, 汪成刚, 李吉涛. 大样本数据模型方法在中小河流流量测验中的应用[J]. 长江科学院院报, 2019, 36(11): 40-44.
CAO Hao, WANG Chenggang, LI Jitao. Application of large sample data analysis method to flow calculation of medium and small rivers[J]. Journal of Yangtze River Scientific Research Institute, 2019, 36(11): 40-44.
[6] PITON G, RECKING A. Effects of check dams on bed-load transport and steep-slope stream morphodynamics[J]. Geomorphology, 2017, 291: 94-105.
[7] KUPFERSCHMIDT C, ZHU D Z. Physical modelling of pool and weir fishways with rock weirs[J]. River Research and Applications, 2017, 33(7): 1 130-1 142.
[8] 吕宏兴, 刘焕芳, 朱晓群, 等. 机翼形量水槽的试验研究[J]. 农业工程学报, 2006, 22(9): 119-123.
LYU Hongxing, LIU Huanfang, ZHU Xiaoqun, et al. Experimental research on airfoil-shaped flow flume[J]. Transactions of the Chinese Society of Agricultural Engineering, 2006, 22(9): 119-123.
[9] 潘志宝, 吕宏兴, 张晓斐, 等. 梯形渠道机翼形量水槽试验[J]. 农业机械学报, 2009, 40(12): 97-100, 143.
PAN Zhibao, LYU Hongxing, ZHANG Xiaofei, et al. Experiment on airfoil-shaped measuring flume in trapezoidal canal[J]. Transactions of the Chinese Society for Agricultural Machinery, 2009, 40(12): 97-100, 143.
[10] 冉聃颉, 王文娥, 胡笑涛. 梯形喉口无喉道量水槽水力性能试验研究[J]. 水力发电学报, 2017, 36(9): 82-90.
RAN Danjie, WANG Wen’e, HU Xiaotao. Hydraulic performance experiment of trapezoidal cut-throated flume in trapezoidal channel[J]. Journal of Hydroelectric Engineering, 2017, 36(9): 82-90.
[11] 王莹莹, 王文娥, 胡笑涛. 矩形渠道梯形薄壁侧堰流量系数及分水研究[J]. 水力发电学报, 2017, 36(3): 38-45.
WANG Yingying, WANG Wen’e, HU Xiaotao. Discharge coefficient and flow division of trapezoidal sharp-crested side weirs in rectangular channel[J]. Journal of Hydroelectric Engineering, 2017, 36(3): 38-45.
[12] 王文娥, 薛城, 胡笑涛. 沟灌三角形长喉道田间量水槽水力特性试验及数值模拟[J]. 农业工程学报, 2019, 35(3): 109-116.
WANG Wen’e, XUE Cheng, HU Xiaotao. Numerical simulation and test of hydraulic performance for triangle long-throat flume for water measurement in furrow irrigation[J]. Transactions of the Chinese Society of Agricultural Engineering, 2019, 35(3): 109-116.
[13] 刘英, 王文娥, 胡笑涛, 等. U形渠道圆头量水柱测流影响因素试验及模拟[J]. 农业工程学报, 2014, 30(19): 97-106.
LIU Ying, WANG Wen’e, HU Xiaotao, et al. Experiment and simulation of factors affecting flow measurement of water-measuring column with round head in U-shaped channel[J]. Transactions of the Chinese Society of Agricultural Engineering, 2014, 30(19): 97-106.
[14] WESSELS P, ROOSEBOOM A. Flow-gauging structures in South African Rivers Part 1: An overview[J]. Water SA, 2012, 35(1): 1-10.
[15] WESSELS P, ROOSEBOOM A. Flow-gauging structures in South African Rivers Part 2: Calibration[J]. Water SA, 2012, 35(1): 11-19.
[16] 王文娥, 廖伟, 陈土成, 等. 堰槽组合设施测流机制试验研究[J]. 水科学进展, 2021, 32(6): 922-932.
WANG Wen’e, LIAO Wei, CHEN Tucheng, et al. Experimental study on the flow measurement mechanism of a weir-flume combination facility[J]. Advances in Water Science, 2021, 32(6): 922-932.
[17] MAHDHAOUI H, CHESNEAU X, LAATAR A H. Numerical simulation of flow through a porous square cylinder[J]. Energy Procedia, 2017, 139: 785-790.
[18] 刘英, 王文娥, 胡笑涛, 等. U形渠道圆头量水柱测流影响因素试验及模拟[J]. 农业工程学报, 2014, 30(19): 97-106.
LIU Ying, WANG Wen’e, HU Xiaotao, et al. Experiment and simulation of factors affecting flow measurement of water-measuring column with round head in U-shaped channel[J]. Transactions of the Chinese Society of Agricultural Engineering, 2014, 30(19): 97-106.
[19] 刘嘉美, 王文娥, 胡笑涛. U形渠道圆头量水柱的数值模拟[J]. 中国农业大学学报, 2014, 19(1): 168-174.
LIU Jiamei, WANG Wen’e, HU Xiaotao. Numerical simulation of water-measuring pillar with round head in the U-shaped channel[J]. Journal of China Agricultural University, 2014, 19(1): 168-174.
[20] 牟献友, 李超, 李国佳, 等. U形渠道直壁式量水槽水力特性数值模拟[J]. 华北水利水电学院学报, 2010, 31(2): 16-19.
MOU Xianyou, LI Chao, LI Guojia, et al. Research on hydraulic characteristics numerical simulation of U-shaped channel straight wall measuring flume[J]. Journal of North China Institute of Water Conservancy and Hydroelectric Power, 2010, 31(2): 16-19.
[21] 郝晶晶, 马孝义, 王波雷, 等. 基于VOF的量水槽流场数值模拟[J]. 灌溉排水学报, 2008, 27(2): 26-29.
HAO Jingjing, MA Xiaoyi, WANG Bolei, et al. Numerical simulation of flow field in flow-measuring flume based on VOF method[J]. Journal of Irrigation and Drainage, 2008, 27(2): 26-29.
[22] 孙斌, 吕宏兴, 张宽地, 等. U形渠道机翼形量水槽水跃数值模拟与试验研究[J]. 实验流体力学, 2013, 27(1): 65-71, 101.
SUN Bin, LYU Hongxing, ZHANG Kuandi, et al. Numerical simulation and experimental research of hydraulic jumps on the airfoil-shaped measuring flume in U-shaped canal[J]. Journal of Experiments in Fluid Mechanics, 2013, 27(1): 65-71, 101.
[23] 李彦浩, 郭豹, 肖业祥. 高水头混流式水轮机转轮泥沙磨损特性模拟研究[J]. 水力发电学报, 2020, 39(2): 112-120.
LI Yanhao, GUO Bao, XIAO Yexiang. Numerical study of hydro-abrasive erosion in high-head Francis turbine runner[J]. Journal of Hydroelectric Engineering, 2020, 39(2): 112-120.
[24] 张成华, 尤建锋, 泰荣, 等. 水泵水轮机水泵断电飞逸过程压力脉动CFD模拟[J]. 水力发电学报, 2020, 39(4): 62-72.
ZHANG Chenghua, YOU Jianfeng, TAI Rong, et al. CFD simulations of pump-trip runaway process pressure pulsation of a model pump-turbine[J]. Journal of Hydroelectric Engineering, 2020, 39(4): 62-72.
[25] 唐茂嘉, 泰荣, 程永光, 等. 甩负荷过程水泵水轮机流激振动数值模拟研究[J]. 水力发电学报, 2022, 41(7): 140-148.
TANG Maojia, TAI Rong, CHENG Yongguang, et al. Analysis of flow-induced vibrations of pump-turbines during load rejection by CFD-FEM simulations[J]. Journal of Hydroelectric Engineering, 2022, 41(7): 140-148.
[26] 宋科, 杨邦成. 无轴轮缘导管涡轮机水动力学性能研究[J]. 水力发电学报, 2021, 40(7): 87-94.
SONG Ke, YANG Bangcheng. Study on hydrodynamic performance of shaftless rim-driven ducted turbines[J]. Journal of Hydroelectric Engineering, 2021, 40(7): 87-94.
[27] 王孝群, 练继建, 马斌, 等. 泄洪洞下游低频噪声数值模拟预测研究[J].水力发电学报, 2022, 41(1): 103-112.
WANG Xiaoqun, LIAN Jijian, MA Bin, et al. Numerical simulations and predictions of low-frequency noises downstream spillway tunnel[J]. Journal of Hydroelectric Engineering, 2022, 41(1): 103-112.
[28] 王莹莹, 王文娥, 胡笑涛, 等. 矩形渠道薄壁侧堰水力特性试验及数值模拟[J]. 水力发电学报, 2016, 35(1): 70-78.
WANG Yingying, WANG Wen’e, HU Xiaotao, et al. Experimental and numerical studies on hydraulic characteristics of sharp-crested side weirs in rectangular channels[J]. Journal of Hydroelectric Engineering, 2016, 35(1): 70-78.
[29] 肖苡辀, 王文娥, 胡笑涛. 基于FLOW-3D的田间便携式短喉槽水力性能数值模拟[J]. 农业工程学报, 2016, 32(3): 55-61.
XIAO Yizhou, WANG Wen’e, HU Xiaotao. Numerical simulation of hydraulic performance for portable short-throat flume in field based on FLOW-3D[J]. Transactions of the Chinese Society of Agricultural Engineering, 2016, 32(3): 55-61.
[30] 冉聃颉, 王文娥, 胡笑涛, 等. 梯形喉口无喉道量水槽水力性能分析[J].水科学进展, 2018, 29(2): 236-244.
RAN Danjie, WANG Wen’e, HU Xiaotao, et al. Analyzing hydraulic performance of trapezoidal cutthroat flumes[J]. Advances in Water Science, 2018, 29(2): 236-244.
[31] 练继建, 任盼红, 刘东明, 等. 明渠完全掺气水流水力特性数值模拟研究[J]. 水力发电学报, 2022, 41(4): 1-8.
LIAN Jijian, REN Panhong, LIU Dongming, et al. Numerical simulations on hydraulic characteristics of fully aerated water flows in open channel[J]. Journal of Hydroelectric Engineering, 2022, 41(4): 1-8.
[32] 吕宏兴, 裴国霞, 杨玲霞. 水力学[M]. 北京: 中国农业出版社, 2002.
[33] 王福军. 计算流体动力学分析: CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004.
Numerical Study of Hydraulic Performance of Weir-flume Combined Device
LING Gang, WANG Wen’e*, WANG Hui, HU Xiaotao
(Key Laboratory of Agricultural Soil and Water Engineering in Arid and Semiarid Areas, Ministry of Education, Northwest A&F University, Yangling 712100, China)
【Objective】The weir-flume apparatus, consisting of a measuring flume and a measuring weir, is an innovative device for monitoring and controlling open channel flow. Installed across channels, it can measure water flow, elevates upstream water level, and enhances ecological connectivity in rivers in diverse geographical conditions. While measurement formulas and hydraulic characteristics have been experimentally investigated for small flow with shallow water depth, there is a lack of study for large flow. This paper aims to bridge this gap by studying the vertical and longitudinal velocity profiles as well as spatial distribution of flow field under high flow conditions. 【Method】The analysis was based on numerical modelling. The FLOW-3D software was used to simulate hydraulic performance of a weir-flume device under 17 flow rates ranging from 10.13 to 200 L/s. From the simulated results we analyzed the impact of flow rate on water depth, Froude number (), and velocities within both the in-groove flow and the weir flow. 【Result】As the flow rate increased, theand velocity in the central longitudinal section of the device initially increased and then tapered off. The flow in the upstream of the device remained stable, withranging from 0.1 to 0.3 and velocities varying between 0.08 and 0.5 m/s. Bothand velocity gradually increased with the increase in flow rate. After entering the device,and flow velocity exhibited a significant surge. A wide range of thin water layers emerged in the downstream of the device, with the maximumand velocities being 3 to 4.6 and 1.05 to 2.06 m/s, respectively. A subdued water jump was observed downstream of the in-groove flow, while the downstream of the weir showed a jet stream with>1. Additionally, diffused water generated a rhomboid wave at the side bank. We derived a formula from the numerical simulations; its maximum relative error was 6.11% for flow rate below 100 L/s, beyond which the relative error gradually increased.【Conclusion】The numerical results obtained from FLOW-3D agreed well with the test data, validating the accuracy and consistency of the derived formula for analyzing measurement data from the weir-flume device. This work bridges a critical knowledge gap, enabling more precise assessment and control of open channel flow under various conditions.
weir-flume combination; numerical simulation; Froude number; hydraulic characteristics; FLOW-3D
1672 - 3317(2023)10 - 0136 - 09
TV8
A
10.13522/j.cnki.ggps.2023049
凌刚, 王文娥, 王惠, 等. 堰槽组合量水设施水力性能数值模拟研究[J]. 灌溉排水学报, 2023, 42(10): 136-144.
LING Gang, WANG Wen’e, WANG Hui, et al. Numerical Study of Hydraulic Performance of Weir-flume Combined Device[J]. Journal of Irrigation and Drainage, 2023, 42(10): 136-144.
2023-02-16
2023-06-16
2023-10-18
国家自然科学基金重点项目(U2243235);陕西水利科技计划项目(2021slkj-8)
凌刚(1997-),男。硕士研究生,主要从事水工水力学研究。E-mail:linggang@nwafu.edu.cn
王文娥(1975-),女。教授,博士生导师,主要从事流体机械与流体动力学、节水灌溉理论与技术研究。E-mail:wangwene@nwsuaf.edu.cn
@《灌溉排水学报》编辑部,开放获取 CC BY-NC-ND协议
责任编辑:赵宇龙

