旋转折射式喷头移动喷洒水量分布计算模型构建与应用

薛绍鹏，葛茂生*，魏福强，张骞文，张廷宁

▪灌溉技术与装备▪

旋转折射式喷头移动喷洒水量分布计算模型构建与应用

薛绍鹏1,2，葛茂生1,2*，魏福强1,2，张骞文1,2，张廷宁1,2

（1.西北农林科技大学 水利与建筑工程学院，陕西 杨凌 712100；2.西北农林科技大学 旱区农业水土工程教育部重点实验室，陕西 杨凌 712100）

【目的】探讨旋转折射式喷头移动喷洒水力特性，优化喷灌机组运行参数和配置。【方法】采用喷灌强度等效拉伸法，构建了基于一次正交多项式拟合的移动喷洒水量分布计算模型，应用该模型对R3000、S3000、O3000喷头进行模拟计算，分析了工作压力（50～150 kPa）、移动速度（20～45 m/h）和组合间距（1.2～6 m）对3种喷头移动喷洒水量分布和均匀度的影响。【结果】①模型计算结果与实测值偏差在5%以内，模型精度较高。②R3000、S3000、O3000喷头移动降水深随距喷头距离的增加而减小，3种喷头移动喷洒均匀度较固定喷洒分别提高11.17%、10.72%和2.36%。③随着工作压力的增大，R3000、S3000、O3000喷头的有效喷灌半径逐渐增大，降水均匀度呈先增大后减小的趋势，最大降低幅度达35.66%，平均降水深和均匀度随移动速度的增大逐渐降低，但3种喷头喷洒均匀度的平均变化幅度仅为0.59%、1.38%、0.99%，说明移动速度对均匀度的影响较小。随着组合间距的不断增大，均匀度呈波动下降的趋势。④考虑工作压力和组合间距双因素影响，R3000、S3000、O3000喷头在低组合间距和高工作压力范围内取得较高的移动喷洒均匀度，在150 kPa/3.6 m、150 kPa/2.4 m、130 kPa/3.6 m的工作压力/组合间距配置组合条件下，喷洒均匀度最高。【结论】等效拉伸法降低了模型构建过程中的拟合次数，提高了计算精度；增大工作压力和降低组合间距有助于提高喷头移动喷洒均匀度。

低压喷头；水量分布；均匀度；移动喷洒；数学模型；组合间距

0 引 言

【研究意义】旋转折射式喷头一般指有压喷灌水流经喷嘴射出，冲击并带动阻尼喷盘旋转，同时水流通过喷盘上具有专门结构设计的流道射出的一种喷头类型。该类喷头具有适用工作压力低，水流破碎充分的特点，被广泛应用于大型时针式与平移式喷灌机等各类移动式喷灌机组[1]。旋转折射式喷头的喷洒水力特性决定了喷灌机组的灌水质量，前人进行了大量的关于旋转折射式喷头喷洒水力特性的研究，包括工作压力、喷盘转速、安装高度等对喷头喷洒水量分布和打击动能分布特性等方面的影响[2-4]。喷灌机原位实测或室内模拟试验是获得喷灌机组移动喷洒水量分布特性的重要手段，但是移动喷洒水量实测易受场地、环境等的限制，且人力与时间投入成本高，难以推广到试验因素较多或试验条件要求较高的情况[5]。因此，尝试通过构建移动喷洒水量叠加模型进行水量分布的模拟计算具有重要意义。

【研究进展】旋转折射式喷头的径向水量分布常呈现明显的峰谷型分布，如单峰或双峰型分布[6]，为获得较均匀的水量分布，需采用多喷头组合和适宜的组合间距，在供水干管方向进行水量叠加[7]。陈震等[8]在实测单喷头水量分布的基础上，通过MALTLAB编程模拟了组合叠加喷洒水量分布特性。朱兴业等[9]采用三次样条插值得到了多喷头组合喷洒水量分布均匀系数。但除了沿供水干管方向进行水量叠加外，喷灌机组在行进过程中，还要沿机组移动方向进行水量的叠加，灌溉区域内每点的实际灌水量，都受到2种水量叠加的共同作用。范永申等[10]通过对喷灌和软管灌溉两用机进行试验，得到了低能耗平移式喷灌机的水量分布和喷灌均匀度变化特征。张以升等[11]实测了特定灌水定额下轻小型平移式喷灌机的移动水量分布特性，发现可以通过调整喷头组合间距和机组行走速度保证喷头在较低工作压力下的喷洒均匀度。Zhang等[12]试验发现振荡波动水压可以提高喷头射程。

固定喷洒条件下的喷头径向水量分布特征曲线是进行移动喷洒水量计算的基础[13]，Zhang等[5]基于实测径向水量分布数据，建立了固定折射式喷头的移动喷洒水量分布计算模型，但其模型的计算过程复杂，不利于推广应用。Dukes[14]研究中曾将喷头径向水量分布简化为三角形、椭圆、矩形和抛物线型等形式，Liu等[15]基于椭圆、三角和抛物线型水量分布假设，建立了配备固定折射式喷头的平移式喷灌机移动喷洒水量分布计算模型，但大量喷洒实测结果表明，喷头的径向水量分布形状较为复杂，随喷头类型、工作压力等的变化呈马鞍形、单峰、双峰等不规则变化[6]，依据简单几何图形表征喷头的径向水量分布不具有代表性。最小二乘法是基于最小化误差平方和的曲线拟合优化方法，能够更真实地反应喷头径向水量分布的峰谷特征[6]，葛茂生等[13]基于最小二乘法拟合建立了一种移动喷洒均匀度计算模型，但基于最小二乘法拟合的多项式往往具有较高的阶数，增加了过拟合风险[16]。

【切入点】旋转折射式喷头在移动喷洒条件下的水量分布与喷洒均匀度存在实测工作量大、易受环境影响，模拟计算精度低、过程烦琐等问题。【拟解决的关键问题】为此，以平移式喷灌机组中应用最广泛的旋转折射式喷头（Nelson R3000、S3000、O3000喷头）为研究对象，采用喷灌强度等效拉伸法，构建基于一次正交多项式拟合的移动喷洒水量计算模型并验证模型精度，将构建模型用于分析喷头工作压力、组合间距、机组移动速度等对移动喷洒水量分布的影响，为优化机组配置和运行参数，提高移动式喷灌机组运行效率提供科学依据。

1 移动喷洒水量分布计算模型构建

1.1 径向水量分布特征曲线

本文以实测水量到拟合曲线正交距离平方和最小为准则，对喷头径向水量分布特征曲线进行正交最小二乘法拟合，与最小二乘法拟合相比，该方法可得到较合理的阶数和更高的拟合精度[17]，基于正交最小二乘法拟合的径向水量分布特征曲线可表述为：

式中：为测点到喷头的距离（m）；()为距喷头距离处的喷灌强度（mm/h）；a为正交多项式回归系数，可根据实测数据采用SPSS或MATLAB软件拟合得到；为正交多项式的阶数；为多项式阶数。利用MATLAB软件设计编写了正交多项式水量分布拟合程序，便于研究和后续计算。

针对江都三站情况，泵站在水轮机工况电机不变极运行时，年平均发电量只略小于电机变极和变频两种运行方式，但所需投资大大减少。因此江都三站在选择反向发电运行方式时应首先考虑采用电机不变极、水泵叶片安放角尽可能小的运行方式，既经济又简单可行。上海电气集团上海电机厂有限公司根据已有成功经验，确定两种配置模式作设计方案，并对其进行对比分析择优使用。两种模式的方案如下：

1.2 移动喷洒水量计算

R3000喷头和S3000喷头为水平旋转折射式喷头，与固定折射式喷头相比，其旋转带来的水流破碎更加充分，使得整体喷洒域的水量分布更均匀[9]，其中S3000喷头的旋转速度更快。O3000喷头是震荡旋转折射式喷头，喷盘在旋转的过程中同时保持一个较小的倾角，使得水流上下振荡，有较为优越的水力性能[8]。为保证相同的喷洒流量，各试验喷头均选用#34喷嘴，喷嘴直径为6.8 mm。具体类型及基本特征见表2。

2.动物分组：75只雄性Sprague-Dawley大鼠按照数字表法随机均分成假手术组、模型组、有氧运动预处理组、HBO处理组和有氧运动+HBO处理组，每组15只。

旋转折射式喷头喷洒范围为圆形，且移动过程中喷头的旋转速度远大于机组的行走速度[11]，故此处可作2点假设以简化计算：①距喷头距离相等的各点处有相同的喷灌强度；②任意1个旋转周期内落在喷洒域某点的水量相同。若喷头所在位置为点，方向为机组行进方向，假设喷头位置不动，为测点移动方向，则轴上任意点的移动喷洒总受水量为该点进入喷洒域的起始点start到完全离开喷洒域的终末点end的总受水量，如图1所示，受水过程可以简化为以该点为垂心垂直于轴的虚线与喷头喷洒域外轮廓线相交得到的虚线段上的历时降水量总和，虚线段可称为喷洒路径。

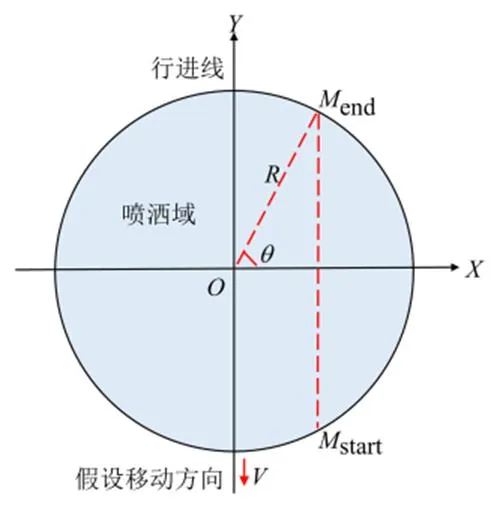
图1 移动喷灌示意

图1中为喷头位置；为测点到喷头行进线的距离（m）；为喷洒半径（m）；start为受水起点；end为受水终点；为喷灌机移动速度（m/h）；为边缘受水点与喷头的夹角（0°<<90°）

1.2.2 等效拉伸系数

以喷头所在位置为圆心，以任意距喷头距离为半径作圆，总是能与喷洒路径和各自交于点和点，如图2所示。根据基本假设，点的喷灌强度数值相等，因此可将点称为一对等效强度点。显然，在喷洒路径上的每一点，均能够在上找到对应的等效强度点，而上任意点的喷灌强度均可通过径向水量分布特征曲线得出，进而可得到喷洒路径上各点对应的喷灌强度。定义点到喷洒路径和径向线上各等效强度点距离的比值为等效拉伸系数。

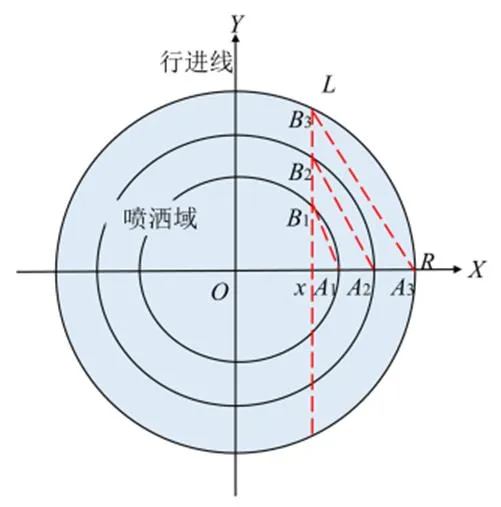
图2 移动路径上等效水量分布假设

图2中为喷头位置点；为测点到喷头行进线的距离（m）；为喷洒半径（m）；为点的喷灌强度等效点；1231、23点为喷灌强度等效点。

在喷灌机组行进过程中，设喷灌机从轴上距喷头距离为的一点出发，其受水区间为start到end的1/2，设机组移动速度为，则任意行进时间时，受水点距轴的距离为，则此时该点距喷头的距离X为：

王维曰“色空无碍，不物物也，默默无际，不言言也。”他以禅宗“空”为基础创作的山水诗纳万象而神韵天成，鸢飞草长而川流不息。契合了禅宗“色即是空，空即是色”的圆融无碍的境界。被王渔阳誉为“字字入禅”的辋川绝句，完整地诠释了中国禅宗对王维诗歌的影响。

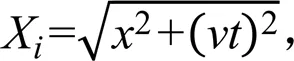
设此时该点在轴上的等效强度点距点距离为Δ，计算式为：

根据对等效拉伸系数的定义，可得在喷洒路径上任意时刻对应的等效拉伸系数为：

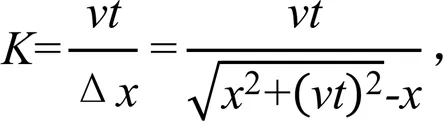
对式（4）变形可得：

——美国调查机构称中国网民患有“坏消息综合症”的比例为62%，与世界平均值41%相比高出21%。这一症状的背后，隐藏着互信缺失、生活无望和内心焦虑。

2.细菌性腹泻。仔猪大肠杆菌病是由致病性大肠杆菌引起的一类传染病，引起仔猪腹泻的主要有仔猪黄痢(早发性大肠杆菌病)和仔猪白痢(迟发性大肠杆菌病)。

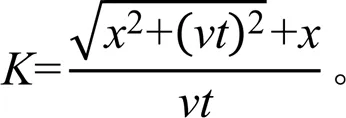
1.2.3 移动喷洒水量

由图10可知，随着组合间距增大，R3000、S3000、O3000喷头降水深逐渐减小，且减小的幅度逐步降低，但喷洒均匀度呈波动下降趋势，在2.4 m喷头组合间距时，有多个喷头的水量分布在典型叠加区域内叠加，使得叠加区域平均降水深明显高于其他喷头组合间距，但较高的降水深易造成土壤侵蚀和水土流失，且3个喷头平均降水深分别为37.09、36.43、31.38 mm，O3000的水量分布更均匀，使得在较低组合间距下平均降水深比R3000、S3000喷头低。当喷头组合间距为3.6 m时，R3000、S3000喷头典型叠加区域内降水深增加较多，而O3000喷头降水深增加较为平缓，水量分布较为均匀，从均匀度曲线看，此时R3000、S3000喷头均匀度的大幅降低，降低幅度达3.14%和6.95%，O3000喷头均匀度降低幅度仅为0.40%。随着组合间距继续增大（≥3.6 m），能够覆盖典型叠加区域内的喷头数仅剩2个，此时区域内水量分布呈随组合间距增大而波动起伏的变化趋势，由于各喷头结构差异，呈现的效果差异明显，R3000、O3000喷头在4.8 m喷头组合间距时均匀度大幅度下降，S3000喷头在6 m喷头组合间距时均匀度大幅下降。故组合间距倾向于较小的配置，此时可以获得更好的均匀度，但同时也意味着较高的降水深和更大的投资。

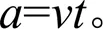
则移动路径上的水量分布函数L()为：

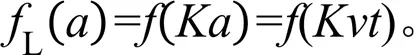
由式（6）和式（7）可得：

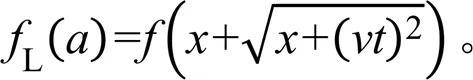
随移动路径上各位置点的拉伸不同，但总的拉伸长度相同，以和长度比（式（9））计算整段移动路径在拉伸后的初始时间和终了时间，如式（10）和式（11）所示，即：

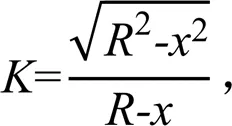
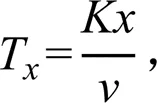
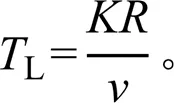
图4(a)和图4(b)为二次功率谱盲检测输出，图4(c)和图4(d)为循环谱检测法频率为0Hz时的盲检测输出，图4(e)和图4(f)为四阶累积量盲检测法的四阶累积量二维切片输出.图4(a)、4(c)、4(e)中输出谱峰均存在多间隔值现象，此现象将导致非合作方检测到接收信号中信号成分不唯一，除大信号残留外还存在其它信号，进而机密信号的隐蔽性降低；图4(b)、4(d)、4(f)中输出谱峰的间隔均为唯一值，且参数特性符合大信号参数特征，机密信号得到隐藏，具有抗盲检测能力.

对喷灌机在受水区间内的总受水时间进行积分，可得在轴任意一点处喷灌机移动受水总量()的上半部分，由基本假设可得，上下部分受水量相同，即积分值的2倍即是该受水点的历时受水总量。设置不变，仅改变值即可得到喷洒路径上任一受水点的历时水量。

1.3 移动组合喷洒均匀度

在单喷头移动喷洒水量分布的基础上，沿供水干管方向进行多喷头水量叠加（图3），假定相邻喷头的间距为，则径向各点位置处的叠加水量计算式[18]为：

亚里士多德十分关注守法所会造成的心灵品质。从政治的目的而言，由于法律对人们的行为而言是一种最普遍而又最正规的约束和引导，所以，立法精神就显得十分重要，不能容许不公正的行为和邪恶的意图。即是说，城邦法律应该引导人们行事公正，并且关注人们美德的成长。所谓公正，就是指人们在城邦中，能够“各自按照自己应得的一份享有美好的生活”。[2](P86)

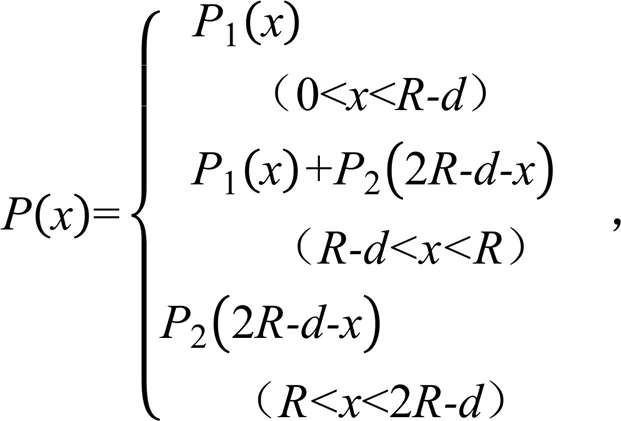
式中：p(x)为单喷头径向移动水量分布函数；R为喷洒半径（m）；d为组合间距（m）；x为组合间距内任一点距首个喷头的距离（m）。

根据组合叠加后各点的水量分布，可进一步计算出旋转折射式喷头的移动组合叠加喷洒均匀度，以Christiansen均匀系数表示，计算式为：

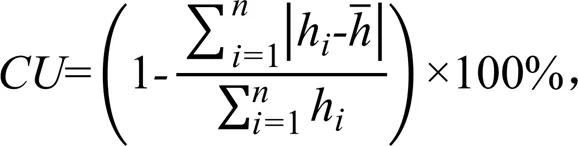
式中：为均匀系数（%）；h为测点水深（mm）；`为平均水深（mm）；为测点数。

单喷头的水量分布是机组的行进喷洒均匀度计算或者喷头配置的技术依据。应用本文构建的移动喷洒计算模型对R3000、S3000、O3000喷头在110 kPa工作压力下的移动喷洒水量分布进行计算，并和定喷水量分布数据进行对比，如图7所示。

2 试验验证

2.1 试验设计

试验在西北农林科技大学旱区节水农业研究院灌溉水力学试验大厅进行，移动喷灌试验平台如图4所示，试验场地平整，试验过程中室内无风，温度适宜。以Nelson S3000喷头为例对模型计算精度进行试验验证。选用6.9 mm喷嘴直径，喷头安装高度距地面1.6 m[2]，分别选取110、130、150 kPa工作压力。试验过程参照标准《GB/27612.3—2011》[19]和《GB/T 19797—2012》[20]。

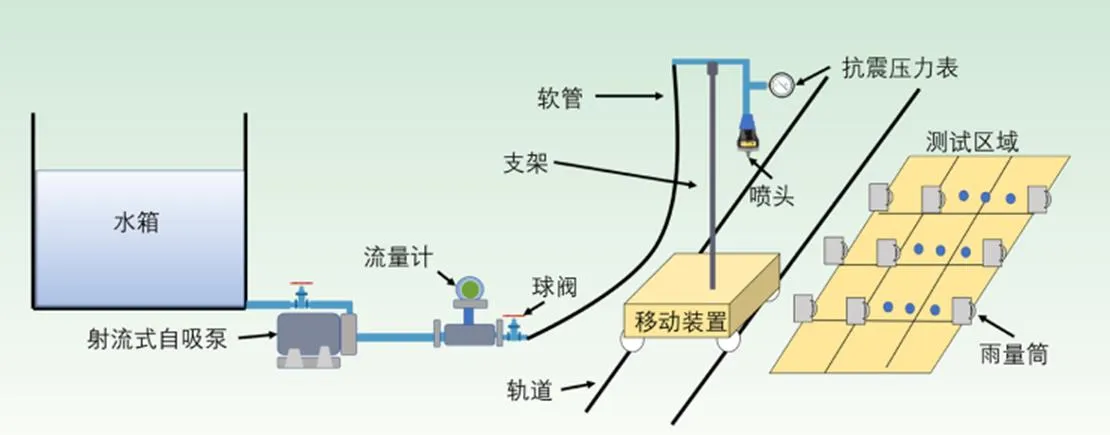
图4 试验装置示意

测试喷头安装在固定支架上，支架下方装有驱动电机和轨道轮，可驱动喷灌装置行走，此装置可用于喷头固定与移动喷洒水量分布测定试验。固定喷洒水量分布测试采用自喷头处引出的3条射线布置雨量筒，射线夹角为20°，布置间距0.4 m，测试时间为10 min。移动喷洒水量分布测试采用垂直机行道方向布置3列雨量筒，每列间距0.5 m，雨量筒布置间距为0.4 m，设计移动时速为30 m/h。

喷洒完成后，采用称质量法计量各测点的喷灌强度和历时降水深，以所布置3列雨量筒所测得的平均喷灌强度确定为该测点的喷灌强度。

工作压力是影响喷灌机灌溉质量的重要因素[2]，但生产厂家给出喷头适用工作压力范围较为模糊（R3000适用工作压力为100～200 kPa，S3000适用工作压力为70～140 kPa，O3000适用工作压力为40～100 kPa），对喷头的应用和选配缺乏有效指导。结合上文构建的移动喷灌水量分布计算模型，分别计算了R3000、S3000、O3000喷头在50、70、90、110、130、150 kPa工作压力下的移动喷洒水量分布，以及喷洒均匀度系数（图8）。

2.2 S3000喷头径向水量分布

通过固定喷洒水量分布测定试验测试得到了S3000喷头在110、130、150 kPa工作压力下的喷灌强度，详见图5。表1为基于正交最小二乘法拟合的S3000喷头径向水量分布曲线的拟合系数和决定系数。

根据涌流理论，当三个条件（挑战性-技巧平衡、清晰的目标和明确的反馈）具备时，涌流体验产生。在口译的过程当中，译员的目标十分清晰，简而言之，即将听到的语言译成另一种语言使双方达到沟通的目标；另外，当译员在译时接受到及时的反馈（如观众的反应、演讲人的眼神等）同时认为自己的口译能力能够胜任要求的时候，理论上译员会进入涌流状态。

图5 S3000喷头径向水量分布

表1 S3000喷头径向水量分布分段拟合系数

2.3 模型验证结果与分析

将拟合系数及喷洒半径、移动速度等相关参数代入式（13）所构建的移动喷洒计算模型计算出径向各点的降水深，初始时间X终点时间L和等效拉伸系数由式（10）、式（11）、式（12）计算，同时与二次拟合移动喷洒计算模型[13]的计算结果对比。图6为线性移动水量分布模型验证结果。

由图6可知，本研究所构建的单次拟合模型计算值与实测值拟合度较高，在相应的降水量上升弯曲段和径向末尾段存在部分误差，在130、150 kPa工作压力时最大误差分别为0.68、0.85 mm，而110 kPa工作压力时最大误差达到2.13 mm，这主要是由水量分布曲线分段拟合对2段连接部分的拟合效果精度较低引起的。在110、130、150 kPa工作压力，本研究模型与实测值相比平均相对误差分别为0.550、0.308、0.468 mm，平均偏差率为4.76%，而采用二次拟合模型[13]的计算值和实测值偏差可达1.99、2.32、2.61 mm。由此可知，基于一次正交多项式拟合的移动喷洒水量分布计算模型通过减少拟合次数，可有效提升模型计算精度。

图6 线性移动水量分布模型验证

3 模型应用

3.1 喷头选用

低压旋转折射式喷头是广泛应用于移动式喷灌系统的喷头类型，根据喷头喷盘旋转所在的平面又可分为水平旋转和震荡旋转喷头，其中最具代表性的是美国Nelson公司生产的R3000、S3000、O3000喷头。

1.2.1 基本假设

在我国，也存在着非婚生子女，而且法律将其分为以下两类:(1)“未婚男女”所生的子女。(2)“已婚男女与别人发生不正当性行为所生的子女”。(最高人民法院《关于对非婚生子女解释的复函》(［74］法办研字第8号))，然而，非婚生子女的认领制度却经历了一个从有(1950年《婚姻法》第15条第2款)到无(1980年《婚姻法》第19条第2款、现行《婚姻法》第25条第2款)的过程。那么，我国是否应重建或恢复认领制度呢?如果应该，则应如何建立呢?本文拟回答这些问题。

表2 喷头类型及基本特征

3.2 固定与移动喷洒水量分布

通过本文移动喷洒水量分布计算模型可计算得到旋转折射式喷头在不同工作压力、组合间距以及移动速度下的移动喷洒水量分布和移动组合叠加喷洒均匀度。

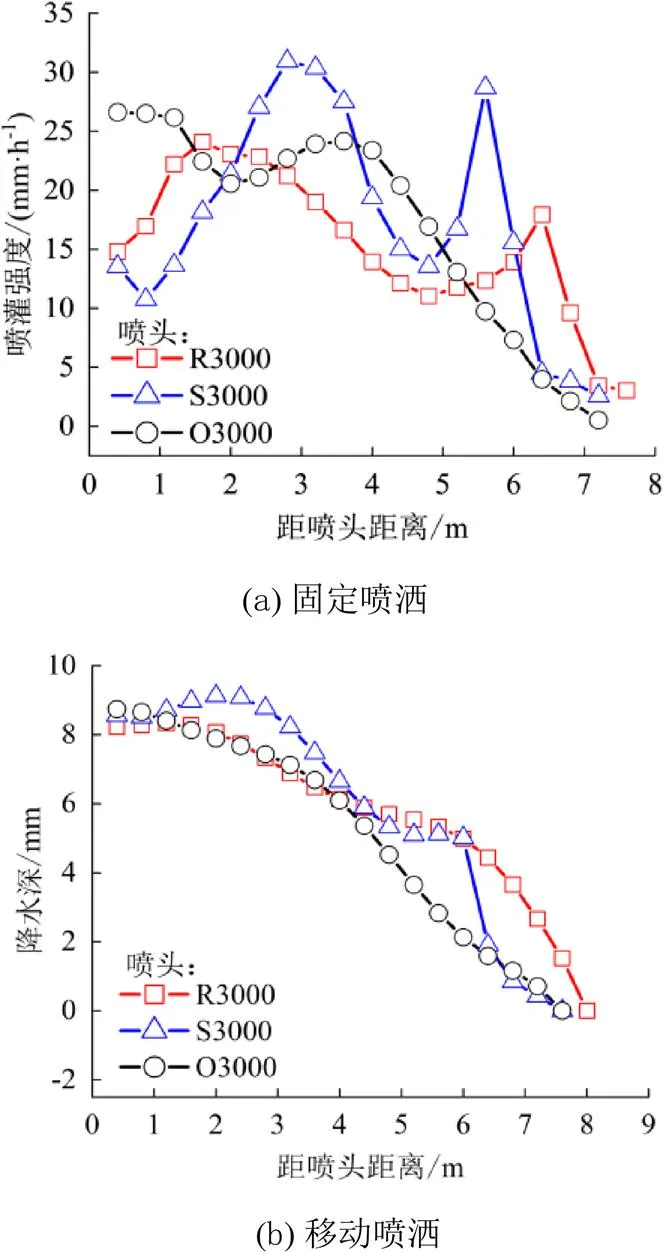
图7 固定喷洒与移动喷洒水量分布对比

由图7可知，移动喷洒水量分布呈抛物线分布，移动降水深随距喷头距离的增加呈减小趋势，与固定喷洒喷水量分布曲线的双峰分布相比，移动喷洒极大削弱了峰值水量分布，移动喷洒过程中，R3000、S3000、O3000喷头峰值降水深分别占平均降水深的137.06%、144.53%、150.94%，与固定喷洒相比，移动喷洒3种喷头峰值降水深分别降低14.96%、23.01%、1.85%，降低了对土壤冲刷的风险和地表积水形成的可能。R3000、S3000、O3000喷头移动喷洒均匀度分别为75.42%、65.26%、58.00%，与固定喷洒相比，移动喷洒3种喷头喷洒均匀度分别提高11.17%、10.72%、2.36%，说明机组行进方向的水量叠加过程可有效提升喷洒均匀度。

3.3 工作压力对移动喷洒水量分布特性的影响

萧飞羽按住转动的钢环凝视鬼算盘，那目光就像穿透了鬼算盘的眼眸看到了鬼算盘的心扉。一旁的武成龙惑然，因为他发现萧飞羽的目光就像历经沧桑般的沉静、事故、精明、睿智，以致他甚至怀疑面对的不是萧飞羽，而是一座见证过古往今来风霜雪雨的巍峨高山。

由图8可知，R3000、S3000、O3000喷头在不同工作压力下的移动降水深曲线均呈抛物线型分布，移动降水深随距喷头距离的增大逐渐减小，旋转折射喷头R3000、S3000在近喷头处2、6 m左右存在微小的峰值降水深，这是由于固定水量分布曲线的双峰在移动过程叠加所致。随着工作压力的增大，R3000、S3000、O3000喷头有效喷灌半径逐渐增大，增加幅度分别为31.25%、26.7%、30%，各喷头的平均降水深和最大降水深随工作压力的增大基本呈上升趋势，平均降水深的变化幅度分别为35.29%、31.66%、19.21%，最高降水深的变化幅度为58.6%、47.87%、24.47%。R3000、S3000喷头降水深的变化趋势类似，与R3000、S3000喷头相比，O3000喷头降水深的增长幅度较低，可能与振荡射流形式有关，灌溉水在喷洒域分布更加均匀。

随着工作压力的增大，降水均匀度均呈先增大后减小的趋势。在130 kPa工作压力下，喷头均匀度呈增加趋势，最大增加段在S3000喷头110～130 kPa处，最大增加幅度为21.21%。而当工作压力高于130 kPa时，均匀度均大幅度降低，最大降低段位于130～150 kPa处，最大降低幅度为35.66%，其中R3000喷头在70 kPa工作压力时达到最大均匀度71.62%，S3000喷头在130 kPa工作压力时达到最大均匀度72.86%，O3000喷头在90 kPa工作压力时达到最大均匀度60.15%。

图8 各喷头不同工作压力下移动降水深和水力性能指标

3.4 移动速度对喷洒均匀度的影响

从图9可以看出，随着移动速度的增大，R3000、S3000、O3000喷头降水深曲线趋于平缓，平均降水深呈对数逐渐降低。当移动速度较低时，各喷头平均降水深较高（移动速度为20 m/h，平均降水深分别为9.24、10.77、8.35 mm）。各喷头任一测点处的移动降水深随移动速度的增大而减小，且减小幅度随移动速度的增加而降低，移动速度在20～25 m/h时，R3000、S3000、O3000喷头处移动降水深减小幅度最大，分别为19.9%、15.82%、20.15%，随着移动速度的增大，各测点的降水历时逐渐减小，使得叠加在该测点的水量减小。

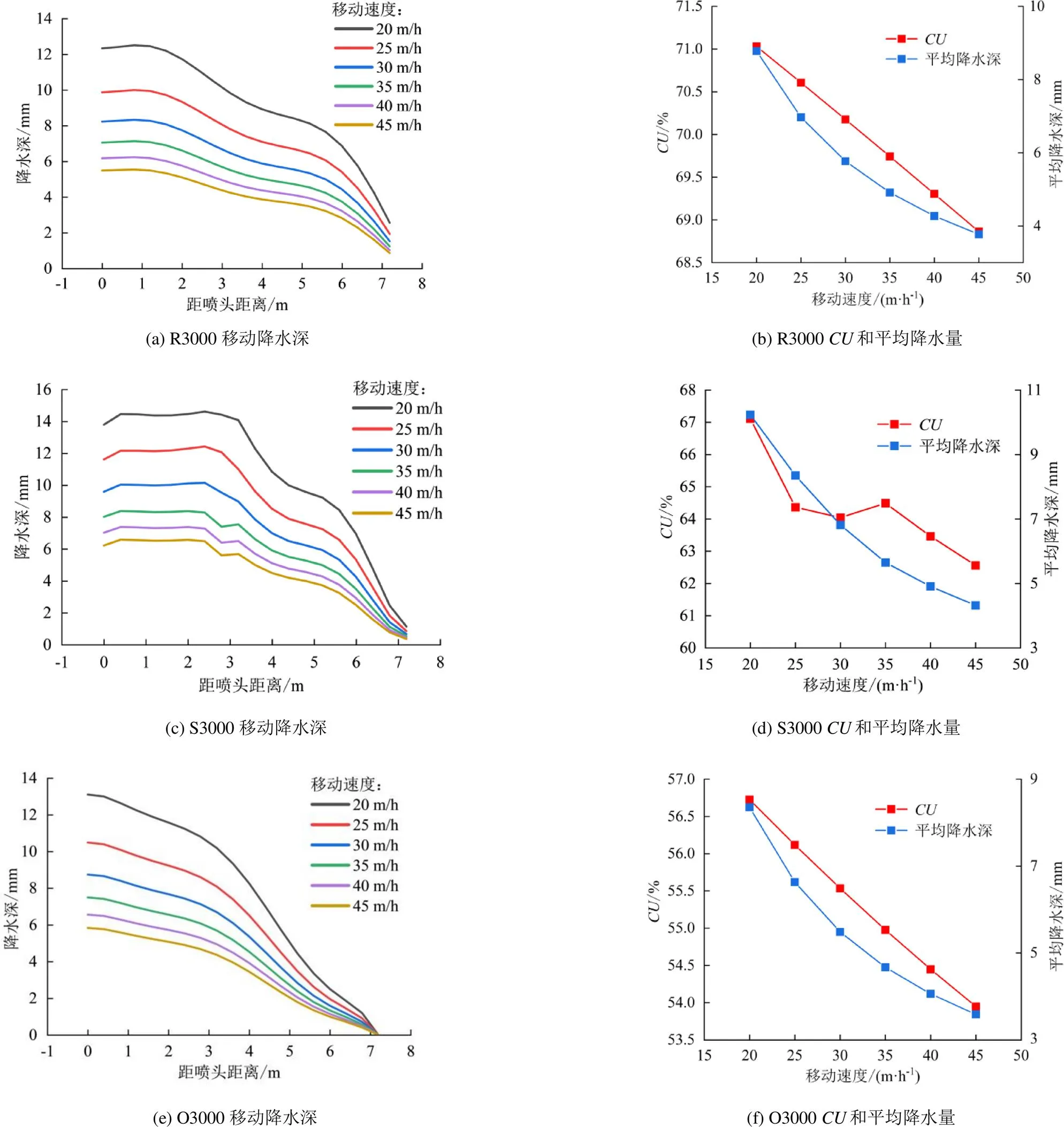
图9 110 kPa工作压力下3种喷头移动降水深和喷洒均匀度

R3000、S3000、O3000喷头喷洒均匀度随移动速度的增大而减小，当移动速度为20 m/h时喷洒均匀度最大，分别为74.93%、67.11%、56.72%，但均匀度的平均变化幅度仅为0.59%、1.38%、0.99%，说明移动速度对喷洒均匀度的影响较小。综上可知，在根据需求平均降水深进行喷灌机移动速度设计时，由于平均降水深在低移动速度时下降幅度较大和均匀度较高的特性，故可适度降低设计移动速度，以提高降水均匀度和平衡由于机组运行和蒸发漂移带来的水量损失。

3.5 组合间距对喷洒均匀度的影响

110 kPa工作压力下，R3000、S3000、O3000喷头的单喷头移动喷洒射程为7.2、7.2、7.6 m，选取2.4、3.6、4.8、6、7.2 m的双喷头组合间距[21]，定义双喷头组合间区域为典型叠加区域，移动过程的径向降水深简化为多个喷头在典型叠加区域内的径向降水深之和。各喷头的组合移动降水深和均匀度见图10。

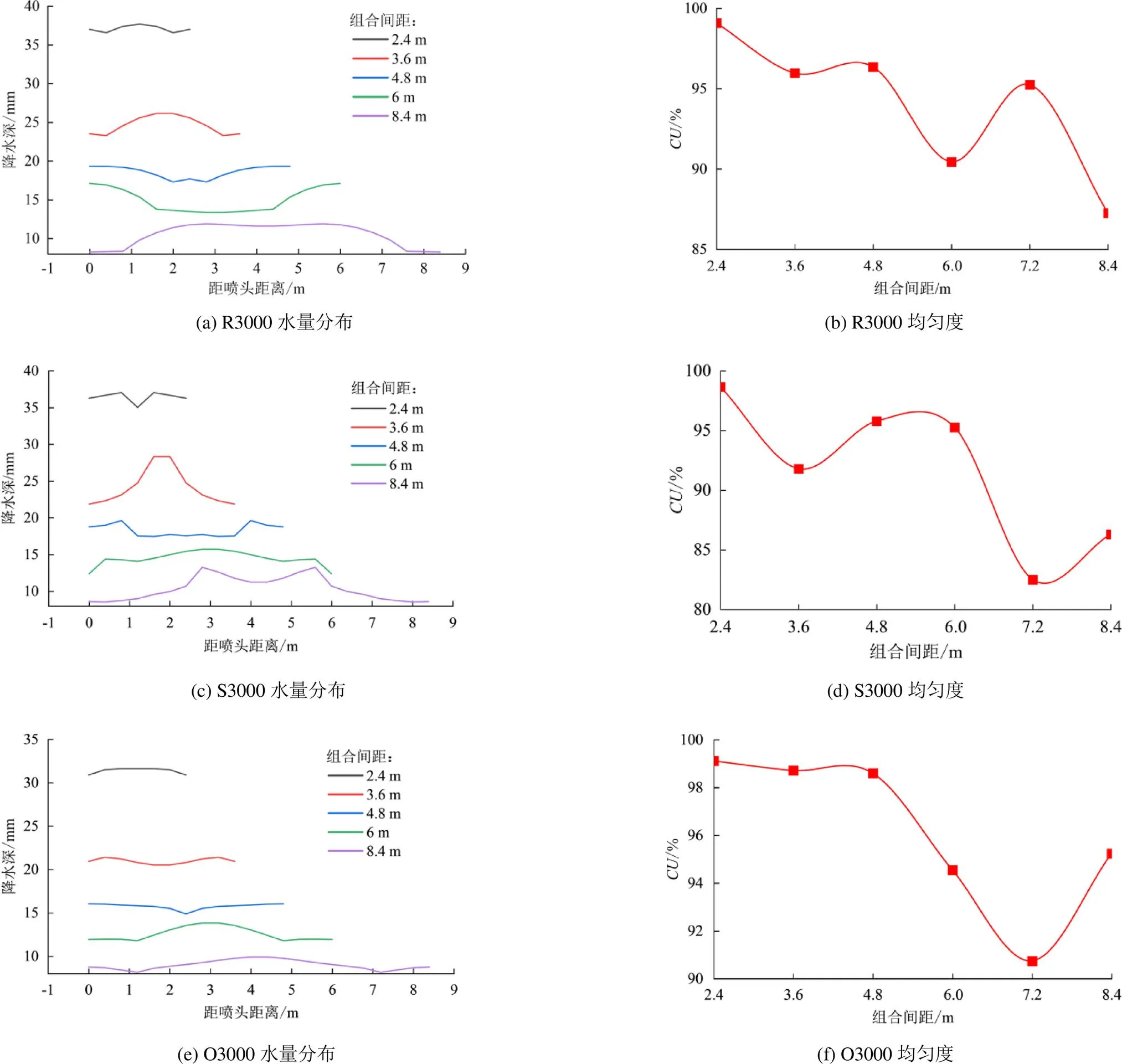
图10 110 kPa工作压力下不同喷头组合间距下3种喷头水量分布与喷洒均匀度

设固定喷洒径向水量分布的拟合函数为()，移动路径上的水量分布函数为f()，将等效拉伸系数带入固定喷洒水量分布函数，设为喷灌机在喷洒路径上任意时刻点到轴的距离。

乌龙矶水库除险加固工程生产生活区现状为耕地，施工前，对可能受到污染、硬化的混凝土拌和场、机械维修厂等场地进行表土剥离，剥离厚度按0.5 m考虑，先堆放于场地一角，并采取彩条布遮盖防尘措施。对生产生活区，采取开挖土质排水沟等措施，排出场地雨水和生产生活污水，防治水土流失。施工机械设备冲洗水等施工用水尽量集中排放，通过环保工程设置的沉淀池处理后循环使用或沉淀处理达标后排入下游河道。生产生活区在结束使用后，需要按要求及时进行施工迹地清理，恢复原有土地功能。

3.6 多参数评价

不同组合间距和工作压力下移动喷洒均匀度见图11。由图11可知，最大喷洒均匀度基本位于组合间距小于6 m和工作压力大于110 kPa范围，R3000、S3000、O3000喷头最大喷洒均匀度分别为99.69%、99.08%、99.58%。以《GB/T 19797—2012》[20]规定的移动喷洒均匀度85%的要求值为限，组合间距低于6 m与工作压力高于70 kPa的喷灌配置下的移动喷洒均匀度基本满足要求。

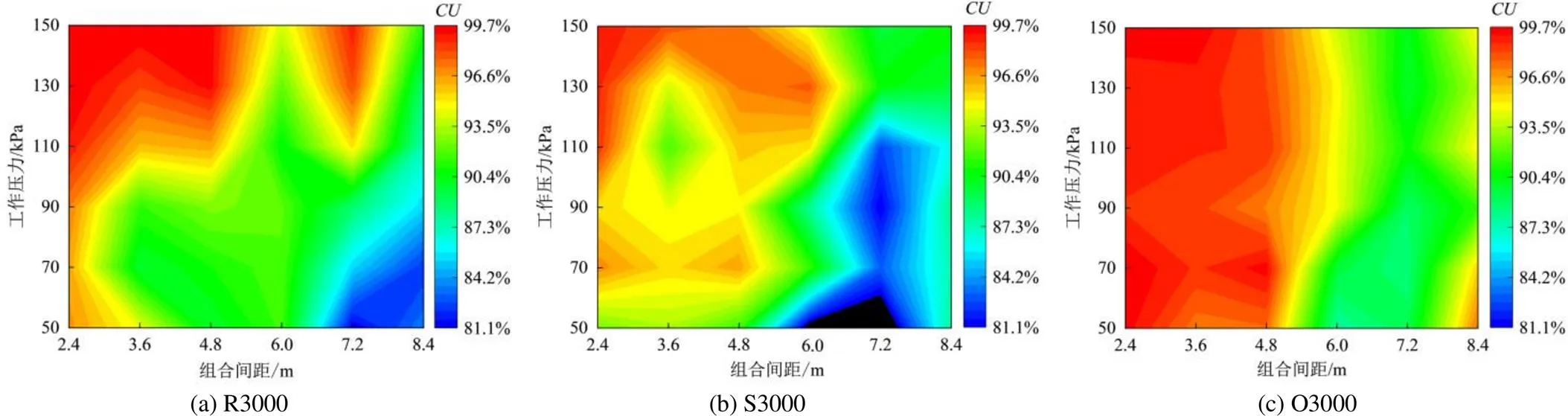
图11 不同组合间距和工作压力下3种喷头均匀度热图

综上可知，工作压力和组合间距的不同配置对移动喷洒水量分布均匀度有明显影响，考虑双因素影响下的大型喷灌机机组配置，R3000喷头的最优配置分别为工作压力150 kPa和组合间距3.6 m，S3000喷头的最优配置分别为工作压力150 kPa和组合间距2.4 m，O3000喷头的最优配置分别为工作压力130 kPa和组合间距3.6 m。

4 讨 论

4.1 移动喷洒水量分布模型的误差来源

喷头的径向水量分布形状随喷头类型、工作压力等的变化呈现马鞍形、单峰、双峰等不规则变化[6]，本研究构建的移动喷洒水量分布计算模型基于固定喷洒水量分布数据，与Liu等[15]基于椭圆、三角和抛物线型水量分布假设建立的平移式喷灌机移动喷洒水量分布计算模型相比，模型精度提高。表明通过水量分布曲线拟合较假设水量分布形式能够进一步降低误差。

与最小二乘法拟合相比，正交最小二乘法可得到较合理的阶数和更高的拟合精度[17]，本研究基于正交最小二乘法构建的移动喷洒水量分布计算模型，模拟精度达95.24%，与葛茂生等[13]基于普通最小二乘法拟合建立的移动喷洒均匀度计算模型相比，模型精度提高0.73%，本研究更为真实地反映了喷头径向水量分布的峰谷特征[6]。此外，应用本研究模型仅进行了1次拟合，极大降低了拟合误差和过拟合的风险，进一步提高了模型精度，降低计算难度。

(2)混凝土底板对组合梁的变形具有一定的抑制作用，但温度应力在某些部位仍然较大，所以应当重视组合箱梁温度效应对结构安全的影响。

本研究中固定喷洒水量分布的实测数据基于稳定和可控的室内条件，而实际喷灌机应用的大田环境存在影响水量分布均匀度的因素较多，模型中暂未考虑大田环境的影响，但根据朱兴业等[21]对旋转折射式喷头特性的研究，上述引入的误差存在但影响并不显著。

4.2 喷灌机配置因素对移动喷洒均匀度的影响

喷灌机移动速度是机组配置的重要因素和变量，对水量分布均匀度有着显著的影响[5, 22]，本研究表明，随着移动速度的增大，喷头降水深曲线趋于平缓，平均降水深呈对数逐渐降低，这与Zhang等[12]研究结果一致，同时，发现喷灌机行走速度与平均降水深负相关，且移动速度对均匀度的影响较小。Zhang等[5]的研究结论表明了这一观点，但不同的是，Zhang等[5]是在特定灌水定额下，而本研究中设定为同一工作压力。

本研究发现，当工作压力高于130 kPa时，均匀度均大幅度降低，最大降低工作压力范围为130～150 kPa，最大降低幅度为35.66%，这与Zhang等[23]文中描述的过高工作压力可能造成集中水量分布和均匀度降低的情况一致。

本研究表明，随着组合间距增大，各喷头降水深逐渐减小，均匀度呈下降趋势，这与Mateos[7]和朱兴业等[21]的研究结论一致，同时朱兴业等[21]认为单喷头降水深曲线末端喷洒水量急速下降是造成均匀度较低的主要原因。

本研究仅针对组合间距、移动速度和工作压力对低压折射式喷头移动喷洒水量分布的影响进行了分析，但喷嘴大小和形状、喷头安装高度等也是影响喷头灌溉质量的重要因素。同时，复杂的大田环境如风速、风向、湿度等造成的蒸发和飘逸损失也是研究的重点，后续将根据田间应用对模型进行补充。

5 结 论

1）与固定喷洒相比，移动喷洒极大削弱了峰值水量分布，R3000、S3000、O3000喷头峰值降水深占平均降水深的14.96%、23.01%、1.85%，喷洒均匀度分别提高11.17%、10.72%、2.36%，证明移动喷灌可以提高均匀度和灌溉效率。

2）随着工作压力的增大，有效喷灌半径逐渐增大；当工作压力高于130 kPa时，3个喷头均匀度最高降幅达35.66%；R3000、S3000、O3000喷头均匀度随移动速度的增大而降低，平均变化幅度为0.59%、1.38%、0.99%，证明移动速度对均匀度的影响较小；随着组合间距的不断增大，均匀度呈波动下降的趋势。

3）R3000、S3000、O3000喷头的工作压力和喷头组合间距配置组合分别为150 kPa/3.6 m、150 kPa/2.4 m、130 kPa/3.6 m时，喷洒均匀度最高。

2014年，青海盐湖工业股份有限公司调整总体经营思路，在巩固既有市场、扩大市场份额的基础上，转变经营思路，上接资源、下接市场，按照不同区域和品种，联合市场优势资源分别与行业龙头企业组建了六大联营公司。其中，四川盐湖化工销售有限公司就是青海盐湖工业股份有限公司和新希望集团有限公司成立的混合所有制公司，已成为中国最大的钾化学品市场营销、物流配送和客户服务的专业经营公司。

（作者声明本文无实际或潜在利益冲突）

[1] 李仰斌, 刘俊萍. 中国节水灌溉装备与技术发展展望[J]. 排灌机械工程学报, 2020, 38(7): 738-742.

LI Yangbin, LIU Junping. Prospects for development of water-saving irrigation equipment and technology in China[J]. Journal of Drainage and Irrigation Machinery Engineering, 2020, 38(7): 738-742.

[2] 赵伟霞, 张萌, 李久生, 等. 喷头安装高度对圆形喷灌机灌水质量的影响[J]. 农业工程学报, 2018, 34(10): 107-112.

ZHAO Weixia, ZHANG Meng, LI Jiusheng, et al. Influence of sprinkler height on irrigation performance of center pivot irrigator[J]. Transactions of the Chinese Society of Agricultural Engineering, 2018, 34(10): 107-112.

[3] OUAZAA S, BURGUETE J, PANIAGUA M P, et al. Simulating water distribution patterns for fixed spray plate sprinkler using the ballistic theory[J]. Spanish Journal of Agricultural Research, 2014, 12(3): 850-863.

[4] SCHWANKL L J, PRICHARD T L, HANSON B R. Reducing Runoff from Irrigated Lands: Soil intake rates and application rates in sprinkler-irrigated orchards[M]. San Diego: University of California, Agriculture and Natural Resources, 2007.

[5] ZHANG Yisheng, GUO Jinjun, SUN Bin, et al. Modeling and dynamic-simulating the water distribution of a fixed spray-plate sprinkler on a lateral-move sprinkler irrigation system[J]. Water, 2019, 11(11): 2 296.

[6] 仵峰, 徐露, 刘焕, 等. 单喷头水量分布函数拟合研究[J]. 水利科学与寒区工程, 2019, 2(2): 20-26.

WU Feng, XU Lu, LIU Huan, et al. Fitting research on water distribution function of single sprinkler[J]. Hydro Science and Cold Zone Engineering, 2019, 2(2): 20-26.

[7] MATEOS L. Assessing whole-field uniformity of stationary sprinkler irrigation systems[J]. Irrigation Science, 1998, 18(2): 73-81.

[8] 陈震, 段福义, 范永申, 等. 喷灌机全喷洒域与叠加域水量分布特性的静态模拟[J]. 农业工程学报, 2017, 33(16): 104-111.

CHEN Zhen, DUAN Fuyi, FAN Yongshen, et al. Static simulation on water distribution characteristics of overlap area and whole spraying area for sprinkler[J]. Transactions of the Chinese Society of Agricultural Engineering, 2017, 33(16): 104-111.

[9] 朱兴业, 袁寿其, 向清江, 等. 旋转式射流喷头设计与性能正交试验[J]. 农业机械学报, 2008, 39(7): 76-79.

ZHU Xingye, YUAN Shouqi, XIANG Qingjiang, et al. Orthogonal experiment on design and performance of a rotational jet sprinkler[J]. Transactions of the Chinese Society for Agricultural Machinery, 2008, 39(7): 76-79.

[10] 范永申, 黄修桥, 仵峰, 等. 喷灌和软管灌溉两用机组水量分布特性与试验[J]. 农业机械学报, 2009, 40(11): 74-77, 123.

FAN Yongshen, HUANG Xiuqiao, WU Feng, et al. Experiment and analysis on water distribution uniformity of machine of sprinkling irrigation and hose irrigation dual purpose[J]. Transactions of the Chinese Society for Agricultural Machinery, 2009, 40(11): 74-77, 123.

[11] 张以升, 朱德兰, 张林, 等. 平移式喷灌机行走速度及喷灌均匀度试验研究[J]. 排灌机械工程学报, 2014, 32(7): 625-630.

ZHANG Yisheng, ZHU Delan, ZHANG Lin, et al. Study on translocating speed and water distribution uniformity of lightweight lateral move irrigation system[J]. Journal of Drainage and Irrigation Machinery Engineering, 2014, 32(7): 625-630.

[12] ZHANG Kai, SONG Bo, ZHU Delan. The influence of sinusoidal oscillating water flow on sprinkler and impact kinetic energy intensities of laterally-moving sprinkler irrigation systems[J]. Water, 2019, 11(7): 1 325.

[13] 葛茂生, 吴普特, 朱德兰, 等. 卷盘式喷灌机移动喷洒均匀度计算模型构建与应用[J]. 农业工程学报, 2016, 32(11): 130-137.

GE Maosheng, WU Pute, ZHU Delan, et al. Construction and application of mobile spraying uniformity model of hard hose traveler[J]. Transactions of the Chinese Society of Agricultural Engineering, 2016, 32(11): 130-137.

[14] DUKES M D. Effect of wind speed and pressure on linear move irrigation system uniformity[J]. Applied Engineering in Agriculture, 2006, 22(4): 541-548.

[15] LIU J P, ZHU X Y, YUAN S Q, et al. Modeling the application depth and water distribution uniformity of a linearly moved irrigation system[J]. Water, 2019, 11(4): 827.

[16] GE Maosheng, WU Pute, ZHU Delan, et al. Application of different curve interpolation and fitting methods in water distribution calculation of mobile sprinkler machine[J]. Biosystems Engineering, 2018, 174: 316-328.

[17] 朱晓东, 鲁铁定, 陈西江. 正交多项式曲线拟合[J]. 东华理工大学学报(自然科学版), 2010, 33(4): 398-400.

ZHU Xiaodong, LU Tieding, CHEN Xijiang. Orthogonal polynomial curve fitting[J]. Journal of East China University of Technology (Natural Science), 2010, 33(4): 398-400.

[18] 吴涤非. 行喷式喷灌机组合均匀度的设计与计算[J]. 华北水利水电学院学报, 1984, 5(1): 40-52.

WU Difei. The design and calculation of resultant uniformity of continuously moving mechanical sprinkley systems[J]. Journal of North China Institute of Water Resources and Electric Power, 1984, 5(1): 40-52.

[19] 国家质量监督检验检疫总局, 中国国家标准化管理委员会. 农业灌溉设备喷头第3部分: 水量分布特性和试验方法: GB/T 27612.3—2011[S]. 北京: 中国标准出版社, 2012.

[20] 国家质量监督检验检疫总局, 中国国家标准化管理委员会. 农业灌溉设备中心支轴式和平移式喷灌机水量分布均匀度的测定: GB/T 19797—2012[S]. 北京: 中国标准出版社, 2013.

[21] 朱兴业, 万景红, ALEXANDER Fordjour, 等. 旋转折射式喷头水量分布与喷灌均匀性试验[J]. 农业机械学报, 2018, 49(8): 145-152.

ZHU Xingye, WAN Jinghong, FORDJOUR A, et al. Experiment of water distribution and uniformity of rotating plate sprinkler[J]. Transactions of the Chinese Society for Agricultural Machinery, 2018, 49(8): 145-152.

[22] DOGAN E, KIRNAK H, DOGAN Z. Effect of varying the distance of collectors below a sprinkler head and travel speed on measurements of mean water depth and uniformity for a linear move irrigation sprinkler system[J]. Biosystems Engineering, 2008, 99(2): 190-195.

[23] ZHANG Lin, MERKLEY G P. Relationships between common irrigation application uniformity indicators[J]. Irrigation Science, 2012, 30(2): 83-88.

Construction and Application of Water Distribution Model for Rotary Refractive Sprinkler Spray Head Mobile System

XUE Shaopeng1,2, GE Maosheng1,2*, WEI Fuqiang1,2, ZHANG Qianwen1,2, ZHANG Tingning1,2

(1. College of Water Resources and Architectural Engineering, Northwest A&F University, Yangling 712100, China; 2. Key Laboratory of Agricultural Soil and Water Engineering in Arid and Semiarid Areas, Ministry of Education, Northwest A＆F University, Yangling 712100, China)

【Objective】Refractive sprinkler spray head mobile irrigation is a widely used irrigation system. In this paper, we proposed a model to calculate its water distribution and hydraulic characteristics for helping optimize its operating parameters and configuration. 【Method】We used the sprinkler intensity equivalent stretching method and constructed a mobile sprinkler water distribution model based on the primary orthogonal polynomial fitting. The model was then applied to the R3000, S3000 and O3000 rotary refractive sprinkler head systems to analyze their water distribution under working pressure ranging from 50 to 150 kPa, moving speed from 20 to 45 m/h, sprinkler spacing from 1.2 to 8.4 m.【Result】① The water depth of all three systems decreased with the increase in sprinkler distance. Compared with a fixed system, the three mobile systems increased spraying uniformity by 2.36% to 11.17%. ② With the increase in working pressure, the effective spraying radius of the R3000, S3000 and O3000 systems gradually increased, while their spraying uniformity increasing first followed by a fall. The average water depth and distribution uniformity of the mobile systems decreased with the increase in moving speed, albeit the change was small ranging from 0.59% to 1.38% for the three systems. With the increase in sprinkler distance, the average water depth and the spraying uniformity decreased in a fluctuating way. ③ Considering the influence of working pressure and sprinkler spacing, the R3000, S3000 and O3000 gave the highest spraying uniformity when the working pressure/distance was 150 kPa/3.6 m, 150 kPa/2.4 m and 130 kPa/3.6 m, respectively.【Conclusion】The equivalent stretching method reduces the number of fittings in model construction and improves modelling accuracy. Increasing working pressure or reducing sprinkler spacing can improve spraying uniformity.

low pressure sprinkler; water quantity distribution; uniformity; mobile spraying; mathematical model; combination spacing

1672 - 3317（2023）10 - 0046 - 11

S275.5

A

10.13522/j.cnki.ggps.2023044

薛绍鹏, 葛茂生, 魏福强, 等. 旋转折射式喷头移动喷洒水量分布计算模型构建与应用[J]. 灌溉排水学报, 2023, 42(10): 46-56.

XUE Shaopeng, GE Maosheng, WEI Fuqiang, et al. Construction and Application of Water Distribution Model for Rotary Refractive Sprinkler Spray Head Mobile System[J]. Journal of Irrigation and Drainage, 2023, 42(10): 46-56.

2023-02-12

2023-05-24

2023-10-16

国家自然科学基金面上项目（52279045）；陕西省青年科技新星项目（2023KJXX-011）

薛绍鹏（1998-），男。硕士研究生，主要从事节水灌溉技术与装备研究。E-mail: 1570096512@nwafu.edu.cn

葛茂生（1990-），男。副教授，硕士生导师，主要从事节水灌溉理论与新技术研究。E-mail: gmsnongshui@126.com

@《灌溉排水学报》编辑部，开放获取CC BY-NC-ND协议

责任编辑：白芳芳