高温后木柱轴压性能试验研究*

康 伟,罗卓卓,张继承

(1.中交一航局第四工程有限公司,天津 300000; 2.长江大学城市建设学院,湖北 荆州 434023)

本文进行落叶松木柱高温后轴向力学性能试验,研究截面类型、温度和恒温时间等对木柱轴向力学性能的影响规律,为合理评价木结构火灾后性能提供科学依据。

1 试验概况

1.1 试件设计与制作

本试验共制备了52根高度相同的木质短柱,包括26根圆形木柱和26根方形木柱,并将48个试件暴露在高温下。所有试件均根据截面类型、温度和恒温时间参数进行标注,详细信息如表1所示。在试件制作过程中,对木柱端的上、下表面进行抛光,使木柱两端完全平整,这样可避免试压过程中柱端局部受力不均匀。试件制作完成后及时密封保存。

表1 试验试件参数

1.2 试验材料与仪器

试验中所用的木材由我国东北落叶松(Larix gmelinii(Rupr.) Kuzen.)原木制成,自然干燥期为一年,考虑到木材的差异性较大,选取了足够的试件进行统计分析。

试验用到的仪器包括:①力学性能试验使用的万能试验机,极限承载力为1 000kN,如图1所示;②自动控制升温的高温炉,如图2所示;③其他辅助仪器,如精度为0.01mm的电子游标卡尺,精度为0.01g的电子秤等。

图1 试验装置

图2 高温炉

1.3 试件的高温处理过程

试件于高温试验炉内进行加温处理,该试验炉为手动输入程序,自动控制升温,最高温度为 1 200℃, 其精度能较好满足试验要求。高温处理完成后对所有试件再次进行称量记录,并准确记录高温处理时间。试件高温处理前后均密封保存。

高温处理完成后,使用1 000kN液压万能试验机对木柱进行压缩试验。为了测量试件在加载过程中的变形情况,在每根方木柱上粘贴4个应变片(ε1～ε4),应变片粘贴前需先去除木柱表面的炭化层和高温分解层。在方木柱的中间高度粘贴2个应变片(ε1,ε2);在侧面中间高度靠近边缘位置粘贴2个应变片(ε3,ε4,命名为拐角位置),以分别获得纵向和横向应变,如图3a所示。对于圆形木柱,在每根圆形木柱中粘贴2个应变片(ε5,ε6),2个应变片均位于试件中心,分别用于测量纵向和横向应变。应变片布置细节如图3所示。

图3 应变片布置

1.4 加载装置与加载制度

木柱在1 000kN液压万能试验机上进行试验,采用DH3816静态应变测量系统进行数据采集,如图1b所示。正式加载前先进行预压以减少系统误差。试验采用连续均匀加载方式,加载速度为1.0mm/min,当荷载下降至极限荷载的85%时试验结束。

2 试验结果与分析

2.1 质量损失率

木材质量损失率测定方法以参考GB/T 13942.1—2009《木材耐久性能 第1部分:天然耐腐性实验室试验方法》为主。

试样高温处理后的质量损失率以百分数计算表示,计算公式如下:

式中:W1为试样试验前的全干质量;W2为试样试验后的全干质量。

经过计算整理得到方木和圆木在不同温度、不同恒温时间作用下的质量损失率,如图4所示。

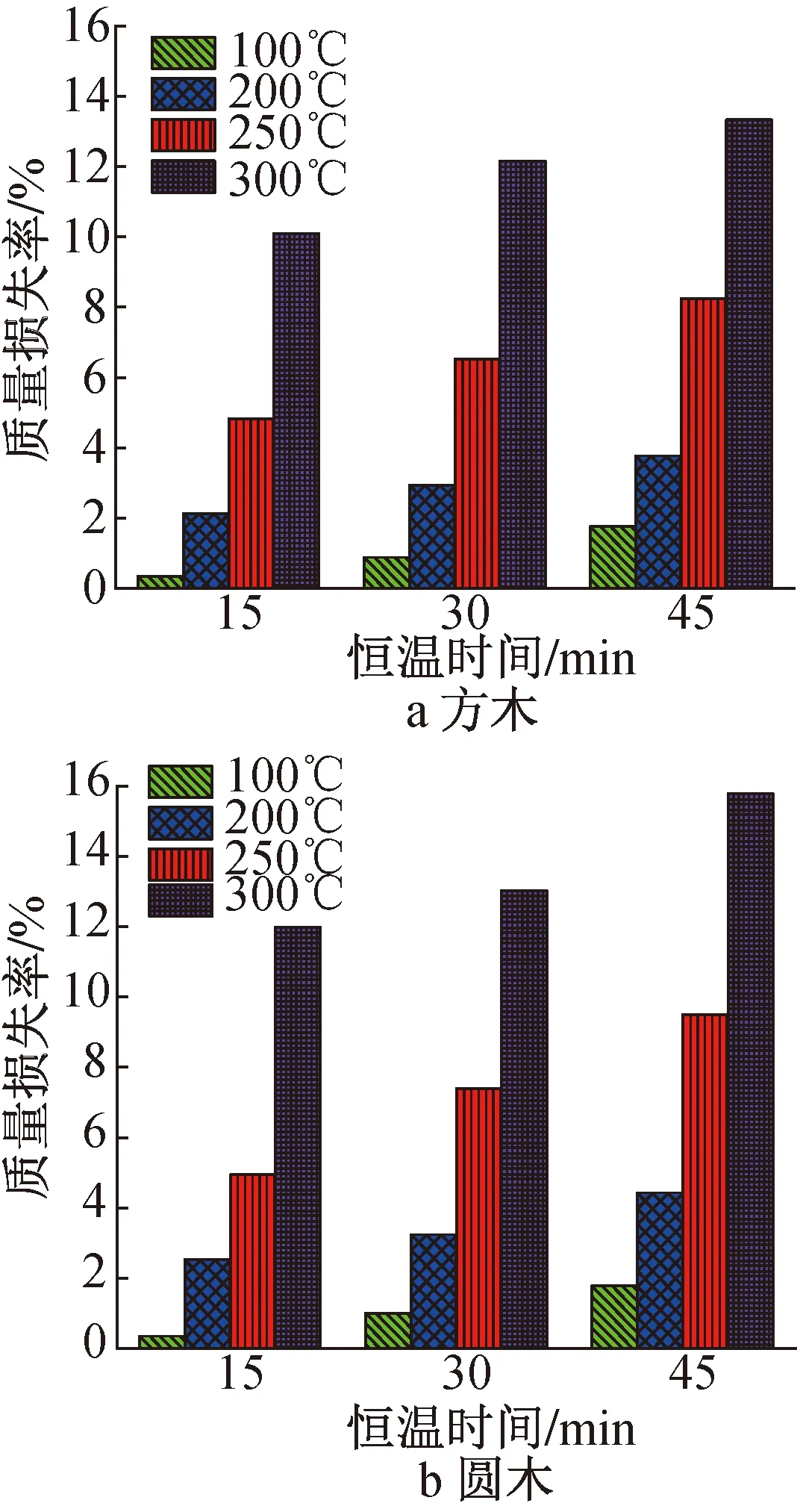
图4 不同温度、不同恒温时间作用下木材质量损失率柱状图

由图4a可看出,方木在恒温时间相同的情况下,温度为100,200℃时,试件的质量损失率变化不明显,此时方木主要为脱水失重,恒温为45min的质量损失率分别为1.75%和3.77%;当温度达到250℃时,质量损失率明显增大,达8.24%,约为温度为200℃时的2.2倍;当温度达到300℃时,质量损失率达13.34%,温度高达300℃时质量损失包括水分蒸发及木材炭化的损失;由图4b可看出,圆木在恒温时间相同的情况下,质量损失率变化规律与方木大致相同,当温度达到250℃时,质量损失率明显增大,达9.5%,当温度达到300℃时,质量损失率达15.79%;总体来说,圆木的质量损失率都比方木大一些。有学者认为当温度>200℃时木材发生了热解反应。木材热解一般在200～250℃发生,木材热解分为纤维素热解和木质素分解2个阶段:第1阶段纤维素快速失重,第2阶段主要是木质素缓慢热解。

在处理温度相同的情况下,如图4a所示,随着恒温时间的延长方木质量损失率也逐渐增大。在处理温度<200℃时,恒温时间对方木质量损失率有较明显影响,当处理温度为100℃时,恒温时间从15min增至45min,方木的质量损失率增加81%;>200℃后,恒温时间对方木质量损失率影响变小,当处理温度为300℃时,恒温时间从15min增至45min,方木的质量损失率增加21%,为100℃处理温度的1/4,这是因为大部分质量损失已在短时间内完成。如图4b所示,恒温时间对圆木质量损失率的影响与方木一致,在处理温度<200℃时,恒温时间对圆木质量损失率有较明显影响;>200℃后,恒温时间对圆木质量损失率影响明显变小。当处理温度为300℃时,恒温时间从15min增至45min,圆木的质量损失率增加24%,是温度为100℃的1/3,且圆木的质量损失率均比方木更高一些。

综上可见,随着处理温度的升高和恒温时间的增加,木柱的质量损失率均呈递增趋势,其中温度对木柱质量损失的影响显著大于恒温时间,且圆木的质量损失比方木高。

2.2 破坏形态

根据破坏现象可将破坏模式分为4种类型,即剪切破坏、劈裂破坏、劈裂破坏与剪切破坏组合和底部压缩破坏,如图5所示。

试验完成后,记录所有试件的极限承载力和破坏模式,详细信息如表2所示。

表2 所有试件试验结果

图5a中方木柱为剪切破坏,可看到斜裂缝发生在方木柱中间高度偏上位置,由表2可看到,有5根方木柱为剪切破坏,所有处理温度为100℃和未经高温处理的方木柱均以剪切破坏失效。由图5b可看出,破坏模式为劈裂破坏,裂缝主要为较大的纵向贯穿裂缝,主要出现在方木柱边缘位置,由表2可看到,有4根方木柱为劈裂破坏,且劈裂破坏试件的处理温度比剪切破坏试件的温度高。由图5c可看出,破坏模式为劈裂与剪切破坏组合,劈裂裂缝出现在方木柱边缘位置,剪切斜裂缝出现在方木柱中间偏上位置,由表2可看到,只有2根方木柱为劈裂与剪切破坏组合失效。图5d中方木柱为底部压缩破坏,压缩破坏表现为底部被压碎,且底部有严重炭化,由表2可看到,只有2根方木柱为底部压缩破坏,且都是处理温度为300℃的试件;底部压碎的方木柱极限承载力明显低于其他试件。

注:Nu表示极限荷载,Per表示极限承载力下降百分率,K表示初始刚度,Δy表示屈服位移,Δu表示极限位移,μ表示延性系数(μ=Δu/Δy)

根据破坏现象可将破坏模式分为3种类型,即剪切破坏、劈裂破坏和底部压缩破坏,比方木柱的类型少1种,如图6所示。

图6 圆木柱破坏模式

图6a中圆木柱为剪切破坏,与方木柱一样,斜裂缝都出现在试件偏上位置,且处理温度为100℃和未经高温处理的圆木柱均以剪切破坏失效。劈裂破坏模式如图6b所示,裂缝未贯穿且裂缝旁边有微小的纵向裂缝,由表2可看到,有6根圆木柱为劈裂破坏,且劈裂破坏试件的处理温度比剪切破坏试件(除试件C-200-15)的温度高。图6c中圆木柱为底部压缩破坏,压缩破坏表现为底部被压碎,且底部有严重炭化,由表2可看到,底部压缩破坏的试件都是处理温度为300℃的试件,与方木柱一样。

总之,未经历高温的试件发生剪切破坏,试件在高温下的破坏模式发生了变化,由表2可看到,处理温度达到200℃时,大部分为劈裂破坏;处理温度达到300℃时,发生底部压缩破坏。

2.3 荷载-应变曲线

试件不同高温温度和不同恒温时间的荷载-应变曲线如图7,8所示。荷载-应变曲线与方形试件中应变测试点间的关系如图7a所示,ε1和ε3的垂直点用实线表示,ε2和ε4的水平点用虚线表示;荷载-应变曲线与放置在圆形试件上的应变测试点间的关系如图8a所示,ε5的垂直点和ε6的水平点分别用实线和虚线表示。如图7,8所示,所有试件的应变均随着荷载的增加而增大。

图7 方木柱荷载-应变曲线

图8 圆木柱荷载-应变曲线

方形木柱在不同温度下的荷载-应变曲线如图7b所示。在方形试件的中心区域,未经历高温试件的横向和纵向最大应变值均大于经历不同温度的试件。对比经历不同温度试件的应变,处理温度越高最大应变值越低,然而,在相同荷载水平下,试件的纵向和横向应变无一致变化,发现温度对应变的影响离散。对于方形试件的角部区域,除拐角区域的S-100-30试件外,未经历高温试件的应变增长速率均大于经历不同温度的试件;未经历高温试件的应变值比经历高温试件的应变值大,此外,除S-300-30试件外,拐角处应变的上升趋势较小,说明试件拐角区域的抗变形性能要优于试件中心区域。与试件中心应变相比,随着荷载的增加,试件拐角处的应变均比中心位置的应变小,试件中心和拐角处的横向应变的极限值均小于纵向应变极限值。

方形木柱不同恒温时间的荷载-应变曲线如图7c所示。在试件中心位置,经历高温的试件极限应变值随着恒温时间的增加而变小;并且随着恒温时间的增加,当在同一荷载水平时,纵向(ε1)应变值在变大,而横向(ε2)应变值在变小。在试件拐角位置,除了S-250-30试件的横向(ε2)应变值之外,应变值变化规律与中心位置一样,总体而言,经历高温试件的应变值均随着恒温时间的增加而变小,与中心位置应变相比,拐角处的应变极限值均小于中心位置。试件纵向的极限应变值始终大于横向的极限应变值。

圆形试件经历高温后不同温度的荷载-应变曲线如图8b所示,对于经历不同温度的圆形试件,在相同荷载水平下,未经历高温的试件横、纵向应变均分别小于经历不同温度试件的横、纵向应变;对比经历不同温度时间的试件可发现,处理温度越高,试件的极限应变值就越小;除C-100-30试件外,试件的应变增长速率随着温度的增加而变小。

圆形试件经历不同恒温时间的荷载-应变曲线如图8c所示,不同恒温时间试件的纵向和横向应变无一致变化,说明恒温时间对高温后圆形试件的横向和纵向应变的影响离散。由图8c也可看出,试件经历的恒温时间越长,其极限应变值越小。总体而言,所有试件的极限应变值均随着温度和恒温时间的增加而变小,对比试件的横向和纵向应变,可发现试件的纵向应变大于横向应变。

3 参数分析

木柱的试验结果如表2所示,K为初始刚度,定义为弹性阶段荷载-位移曲线的斜率,弹性阶段的初始刚度是物体在弹性阶段抵抗外力变形的能力,可表示为K=P/Δ,在本文中,轴向荷载P为40%的极限荷载(Nu)。用延性系数μ(μ=Δu/Δy)表示试件的延性。屈服位移(Δy)通过使用轴向荷载与垂直变形曲线的割线获得,该曲线穿过轴向荷载达到极限荷载的75%(0.75Nu)的点。极限位移(Δu)对应荷载-位移曲线上的极限荷载(Nu)。

3.1 温度的影响

不同的处理温度对木柱极限承载力的影响如图9所示,如表2所示,用极限承载力下降百分率(Per)表示高温处理后试件极限承载力的下降比例。由图9a可知,当恒温时间相同时,方木柱的极限承载力随着温度的升高而降低;从100℃升至200℃时,木柱极限承载力下降较平缓,处理温度>200℃后,极限承载力大幅度下降。但不同恒温时间作用下降低幅度不同,当恒温时间为15min时,在处理温度为100,200,250,300℃下,木柱的极限承载力分别比未经历高温木柱(S-常温)下降5.0%,8.5%,23.9%,47.3%。

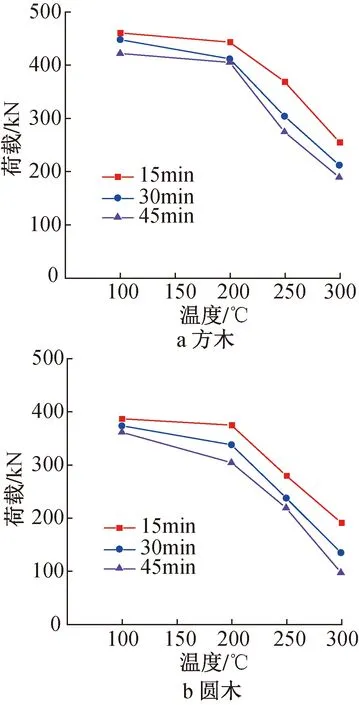
图9 荷载-温度曲线

如图9b所示,圆木柱的极限承载力随处理温度的变化规律与方木柱一致,极限承载力均在温度200℃前下降幅度较小,>200℃后大幅度下降。当恒温时间为15min时,在处理温度为100,200,250,300℃下,圆木柱的极限承载力分别比未经历高温木柱(C-常温)下降1.5%,4.5%,28.8%,51.3%,可见当温度>200℃后,极限承载力下降变快。圆木柱和方木柱的极限承载力随温度的变化规律与2.1节中质量损失率的变化规律一致。

综上可见,当木柱经历高温时,木柱的极限承载力都会降低,且处理温度>200℃时极限承载力下降幅度变大;方木柱的极限承载力均大于圆木柱,说明方木柱的轴心受压能力优于圆木柱;此外,由表2可看出,圆木柱在高温作用下的极限承载力下降幅度大于方木柱,说明高温对圆木柱极限承载力的影响比对方木柱的更大。

3.2 恒温时间的影响

不同的恒温时间对木柱极限承载力的影响如图10所示,如图10a所示,温度为100℃时,当恒温时间从15min增至45min,方木柱的极限承载力下降幅度很小,为8.4%;温度为200℃时,方木柱极限承载力下降幅度与100℃时相差不大,说明当温度很低时,恒温时间的增加对方木柱的极限承载力影响很小。温度为250,300℃时,恒温时间从15min增至45min,方木柱极限承载力分别下降25.7%和26.2%,与100℃相比,方木柱极限承载力快速下降,说明当处理温度>200℃时,恒温时间对方木柱的极限承载力有很大影响。

图10 荷载-恒温时间曲线

如图10b所示,圆木柱的极限承载力总体趋势呈现为随着恒温时间的增加而降低,但降低幅度不相同,温度为100℃时,当恒温时间从15min增至45min时,圆木柱极限承载力下降6.6%;温度为250℃或300℃时,恒温时间从15min增至45min,圆木柱极限承载力分别下降21.9%和49.6%。与方木柱相比,圆木柱极限承载力下降幅度大于方木柱,这表明恒温时间对圆木柱极限承载力的影响比对方木柱的更大。

4 结语

1)随着处理温度的升高和恒温时间的增加,木柱的质量损失率均呈递增趋势,其中圆木柱的质量损失率总体高于方木柱,且温度对木柱质量损失的影响显著高于恒温时间。

2)处理温度<200℃的木柱呈剪切破坏,处理温度>200℃的木柱呈劈裂破坏和底部压缩破坏,且方木柱还出现劈裂和剪切组合破坏;总体来说,高温使木柱的破坏模式发生改变。

3)所有试件的极限应变值均随着温度和恒温时间的增加而变小,方木柱拐角区域的抗变形性能要优于中心区域;试件的纵向极限应变值始终大于横向极限应变值。

4)木柱经历高温后极限承载力下降,试件极限承载力平均下降21%,圆木柱极限承载力下降幅度大于方木柱极限承载力下降幅度。