结构随机振动时域响应统计特征分析的多项式维数分解法
刘 凡, 肖 进, 韩 波, 赵 岩*,4
(1.中南林业科技大学 土木工程学院,长沙 410004; 2.大连理工大学 工程力学系,大连 116024;3.北京宇航系统工程研究所,北京 100076; 4.大连理工大学宁波研究院,宁波 315016)
1 引言
工程结构常受风荷载、波浪力和地震等随机激励作用,准确评估结构在平稳和非平稳随机激励作用下的响应,对提高结构的安全性和可靠度具有重要意义。功率谱是随机激励的一种常用描述方法,通过对随机激励的观测,已经建立了风荷载、波浪力和地震等随机激励的功率谱模型[1]。根据随机激励的功率谱模型,可将功率谱作为输入,利用虚拟激励法在频域内进行随机振动分析,从而得到结构随机振动响应的功率谱和标准差[2]。然而在一些情况下,难以直接将功率谱作为输入,而将时域内的随机激励样本作为输入更为有效[3]。根据随机激励的功率谱模型生成时域样本后,结合不确定性量化分析方法便可得到结构随机振动响应的统计特征。三角级数叠加TSS(Trigonometric series superposition)法是生成时域样本的常用方法,该方法结合蒙特卡罗模拟MCS(Monte Carlo simulation)可以得到可靠的结构响应统计特征。TSS在每个样本中需要较多数目的随机相位才能得到理想的结果,增大了概率空间内的积分维度。MCS需要大量的样本才能得到可靠的结果,计算成本高。针对这两种方法的不足,诸多学者提出了新的随机振动时域响应统计特征分析方法。陈建兵等[4-6]将TSS中的圆频率和相位均视为随机变量,建立随机过程的随机谐和函数表达,得到了结构在地震作用下的响应标准差。Yu等[7]根据车桥耦合系统中的轨道不平顺谱利用随机谐和函数生成时域样本,并采用概率密度演化方法进行了车桥耦合系统非平稳随机振动分析。为了减少TSS中的随机变量数目,Liu等[8]利用较少数目的基本变量构成正交随机变量,采用随机函数来生成平稳和非平稳随机激励的时域样本,并结合概率密度演化方法实现了结构在非平稳地震作用下的响应统计特征分析。在文献[8]的研究基础上,Chen等[9]利用建立的直接概率积分方法,以随机函数生成的时域加速度样本为输入,实现了结构在非平稳地震作用下的响应分析。
概率空间内的高维积分问题是结构随机振动时域响应分析中面临的主要困难。在前述的改进方法中,主要通过减少TSS中随机变量数目并结合高效的不确定性量化方法来降低分析难度和提高效率。同样针对高维积分问题,Rahman[10]利用维数分解和Fourier展开,建立了随机计算中的多项式维数分解PDD(Polynomial dimensional decomposition)法。该方法通过对具有更少随机变量的函数进行组合,实现对原随机函数的逼近,已在具有不确定参数结构的特征值问题[11]、频域响应分析[12,13]和随机结构动力响应分析[14]等不确定性量化分析中得以应用。本文针对TSS中随机相位引起的高维积分问题,建立了结构随机振动时域响应统计特征分析的PDD法。建立的方法构造了结构随机振动响应的PDD展开模型,通过该模型能够得到结构响应的统计特征以及概率密度,且避免了概率空间内的高维积分和大量样本的时域响应分析。
2 随机激励的建模
对于功率谱为Sf(ω)的平稳随机激励f(t),可利用TSS方法由功率谱生成时域样本
(1)
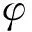
对于非平稳随机激励f(t),其演变功率谱Sf(ω,t)通常由平稳随机激励的功率谱调制而成
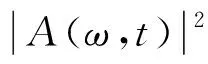
(2)
式中Sf(ω)为平稳随机激励的功率谱,A(ω,t)为调制函数。
此时,利用TSS方法可以生成非平稳随机激励的时域样本
(3)

3 随机激励作用下的结构运动方程
利用第2节中随机激励的建模,可将结构在随机激励作用下的运动方程表示为
(4)



4 随机振动响应的维数分解和Fourier多项式展开

(5)

采用正交多项式基底将式(5)的成员函数进行Fourier多项式展开,并取前m阶截断,得到成员函数的近似显式表达
(6)
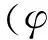
(7)
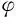
计算得到展开系数后,结构响应的标准差可由各项展开系数Ci1…idj1…jd(t)的平方求和后开方得到。利用式(5,6),可以构造结构随机响应的PDD展开模型
(8)
得到结构响应的PDD展开模型后,根据多项式基底随机变量的概率密度函数生成样本,可由简单的数值运算得到结构响应的近似样本值,进一步得到响应的概率密度。
5 L0(t)和Ci1…idj1…jd(t)的计算
为了减少计算L0(t)和Ci1…idj1…jd(t)时的概率空间积分维度以及实现无显式表达式函数的积分,采用降维积分结合高斯数值积分计算L0(t)和Ci1…idj1…jd(t)。

(9)
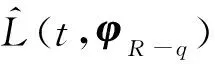
(10)
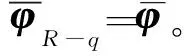
(11)
此时,方程(11)可以采用时域内的逐步积分方法进行求解,也可以采用振型叠加法进一步提高计算效率。

(12)
(13)
式中wnki(i=1,2,…,R-q)为积分节点的权重系数,p为单个变量的积分节点数目。
6 数值算例
6.1 单自由度系统


图1 单自由度系统Fig.1 Single-degree-of-freedom system
图2和图3分别给出了PDD方法和MCS计算得到的系统位移均值、标准差和t=15 s时的概率密度。可以看出,PDD方法能够得到与MCS非常吻合的结果,表明PDD方法具有足够的精确性。MCS需要进行105次时域响应分析,而PDD方法仅需401次时域响应分析,表明PDD方法的分析效率优势更为显著。
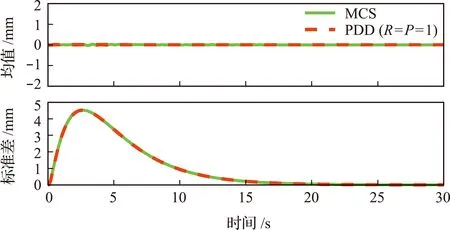
图2 位移均值和标准差Fig.2 Mean and SD of displacement
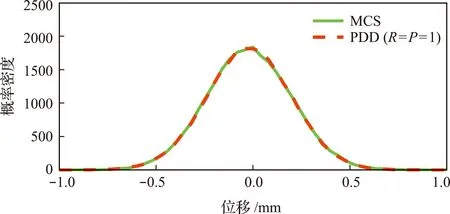
图3 t=15 s时的位移概率密度Fig.3 PDF of displacement when t=15 s
6.2 20层框架结构


图4 20层框架结构Fig.4 Twenty-story frame structure
(14)
式中S0=0.01 m2/s3,ζg=0.6,ωg=7.8 rad/s,ω∈[0,20π];g(t)为调制函数,满足
(15)
式中c1=1.86,c2=0.32,Ta=2.27 s。
分别采用MCS(105个样本)和PDD(R=P=1,m=3,p=3)方法进行结构顶层位移响应的统计特征分析。将分析频率ω离散为400个频率点,分析时间为0 s~50 s,时间步长取0.02 s。
图5给出了结构顶层位移的均值和标准差,可以看出,PDD方法能够得到与MCS非常吻合的位移均值和标准差。顶层位移响应的均值趋近于水平直线,而位移响应的标准差存在明显的上升和下降阶段。PDD方法共进行了801次结构时域响应分析,而MCS进行了105次结构时域响应分析,表明PDD方法具有非常高的分析效率。

图5 顶层位移响应的均值和标准差Fig.5 Mean and SD of displacement of the 20th story
图6给出了t=10.0 s时的顶层位移概率密度曲线,PDD方法计算得到的概率密度与MCS模拟结果吻合较好。可以看出,位移概率密度峰值出现在位移接近于0的位置,且与正态分布的概率密度曲线较为接近。图7给出了顶层位移概率密度演化曲线,结合图5的标准差曲线可以看出,当结构位移响应标准差显著增大时,相应的概率密度显著减小。当位移响应标准差趋近于0时,位移概率密度值逐渐增大,最终趋于稳定。图8给出了顶层位移概率密度等高线,在t=5 s附近位移的概率密度最为分散且取值较小。从图5可以看出,在该时刻附近,顶层位移的标准差最大。

图6 顶层位移概率密度(t=10.0 s)Fig.6 PDF of the displacement of the 20th story

图7 顶层位移概率密度演化Fig.7 PDF evolution of the displacement of the 20th story
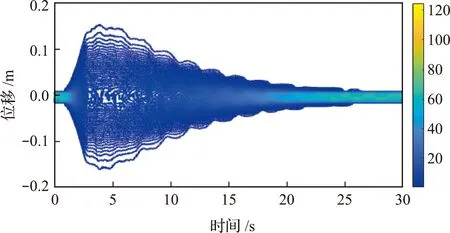
图8 顶层位移概率密度等高线Fig.8 Contour of PDF of displacement of the 20th story
7 结 论
本文针对随机激励作用下结构随机振动响应统计特征分析,利用维数分解和Fourier展开构造出结构响应的PDD展开模型,提出了结构随机振动时域响应统计特征分析的多项式维数分解法,建立的方法可以得到结构响应的统计特征以及概率密度。数值算例中,进行了单自由度系统和20层框架结构在非平稳随机激励作用下的响应分析,算例结果表明,本文方法能够得到与蒙特卡罗模拟非常吻合的结果且具有很高的计算效率。本文方法可以为非平稳随机激励作用下的结构响应分析和可靠度估计提供新的策略。本文主要针对线性结构动力响应的统计特征进行了研究,PDD方法在非线性结构动力响应分析中的应用需要进一步研究。

